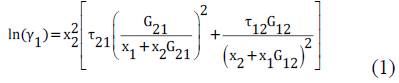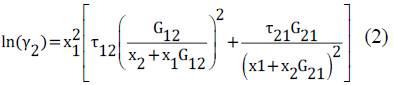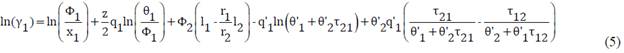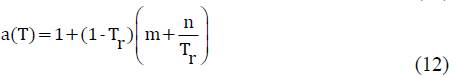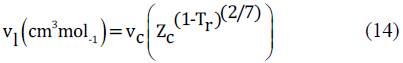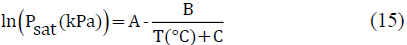1. Introduction
The increasing world energy demand has been historically covered by fossil fuels, but in recent years the ecological repercussions of fossil fuels as energy sources have make the engineers and scientists to turn their attention to renewable energy sources [1]. Bio-ethanol, as a clean, condensed and renewable fuel, is gaining increasing attention, mostly through its major environmental benefits [2].
The worldwide bio-ethanol production is increasing constantly [3], and with it the design, rating and optimization of old and new process technologies for ethanol purification are necessary. To successfully develop new processes, such as pressure-swing distillation, extractive distillation, adsorption with molecular sieves and vacuum membrane distillation, the implementation of simulations for the conceptual design is one of the most important stages. For ethanol production processes, at any scale, an accurate and flexible thermodynamic model for the process simulations is required, a single failure in thermodynamic calculations may cause significant error propagations leading to false solutions or simulation failures [4].
In the case of ethanol separation from water, the binary system has been widely investigated, mostly at atmospheric pressure and high temperatures [4]. Some authors report experimental data for low pressures [5], and adjust binary interaction parameters for excess Gibbs energy models using quadratic form for their temperature dependency. Even so, the quadratic form proposed is not flexible or compatible with most of the process simulators available and widely used worldwide for process synthesis. In this study we present a new set of binary interaction parameters for two excess Gibbs energy models, NRTL (Nonrandom Two Liquid Theory) and UNIQUAC (Universal Quasi-chemical Theory), at low pressures. The binary interaction parameters are adjusted to be easily implemented in many thermodynamic and process simulators due to the simple temperature dependency form proposed.
NRTL and UNIQUAC were chosen for this study, these models are useful in process design due to their accuracy in Azeotropic (non-ideal) systems such as ethanol-water, propanol water, n-butanol-water and many others [6]. WILSPN model is also commonly used due to is simplicity, but considering the actual computation capabilities and reliability its implementation doesn't result suitable, in great part because more accurate results can be achieved from NRT and UNIQUAC models instead.
The first aim of this study is to summarize the isobaric VLE experimental data and azeotropic point reported at 3 different under-atmospheric pressures for the ethanol-water system [5] (13.15, 19.71 and 101.32 kPa). This study also includes a thermodynamic consistency test, using the Redlich-Kister method, for the data used in the parameters regression. The second aim is to present new, flexible and accurate binary interaction parameters, with errors of less than 1%, for the NRT and UNIQUAC excess Gibbs energy models, at low pressures in a temperature dependency form compatible with most of the process simulators used by process engineers to design ethanol separation and purification. The third aim is to provide the parameters and constants for the detailed thermodynamic modeling of the ethanol-water system using polar-SRK (polar fluid Soave-Redlich-Kwong equation of state) for vapor phase and NRTL or UNIQUAC for liquid phase with the new parameters adjusted for low pressures in a suitable way to be implemented in design, optimization and rating of processes.
2. Methodology
The thermodynamic modeling and calculations were developed using high performance hardware: 128 GB RAM DDR3, Two processors Intel® Xeon sixteen core 2.0 GHz. The software used was: python 3.4®, the codes implemented were supplied by S&SE (Smart and Simple Engineering) company and Aspen properties® V8.6 provided by the Universidad Nacional de Colombia. The software was executed using the 100% of computation power available (32 cores x 2.0 GHz).
2.1 Experimental Data
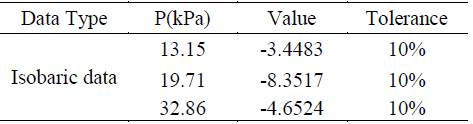
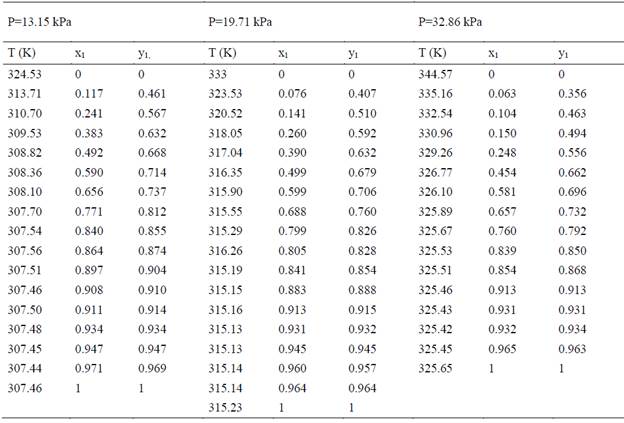
The experimental data used for this study is of two types: isobaric data at 3 different under-atmospheric pressures (13.15, 19.71 and 32.86 kPa). Table 1 and azeotropic points at 17 different under-atmospheric pressures (Table 9).
For the data presents in the Table 1: the pressure measurements have an accuracy of ±0.01 kPa, the temperature values reported have an accuracy of ±0.01 K and the molar fractions has an uncertainty of about ± 0.001.
2.2 Thermodynamic modeling
Most of the sources for bioethanol production processes are fermentation broths [8]. The purification of the ethanol from the aqueous non-ideal mixtures requires an accurate thermodynamic approach for its modeling. Without a reliable model the simulation will get inaccurate results leading to bad designs and finally high economic losses.
This work presents an accurate model to simulate the water-ethanol non-ideal system at under-atmospheric pressures. The Equations of state and activity models are summarize, as well as the constants and parameters involved.
Table 1 Isobaric experimental data for 3 under-atmospheric pressures (13.15, 19.71 and 32.86 kPa) [6]
2.2.1 Activity models
The activity models considered for the liquid non-ideal phase of the binary mixture ethanol-water are NRTL (Nonrandom Two-Liquid Theory) and UNIQUAC (Universal Quasi-chemical Theory). These excess Gibbs energy models have been widely used to reproduce accurately the behavior of water-alcohols systems [5], [9].
Another model available for its use is the WILSPN model sometimes preferred due to its simplicity and faster implementation, even so, WILSPN model is not accurate enough and with the actual computational capacity, due to tis reason the use of NRTL or UNIQUAC is currently both fast and reliable.
For this highly non-ideal binary system, NRTL and UNIQUAC models are suitable for the consideration of the azeotropic point, which is considerably sensible to changes in the system pressure.
2.2.1.1 NRTL
The NRTL model used for this study corresponds to the expanded form for binary systems to determine the activity coefficients of ethanol and water in the mixture. The activity coefficients can be determined with the equations (1) and (2)[9]
Here τij are the dimensionless interaction parameters, calculated using the binary interaction parameters adjusted and presented in this study, aij and bij are the binary interaction parameters adjusted according to the particular conditions, in this case low pressures. cij =cji are called non-randomness parameters, in this case set to 0.3.
The quadratic form presented in 2011 by E.C. Voutsas, et al [6] to estimate the interaction parameters is accurate and consistent but its form is not universal in its temperature dependency.
The form of the equation (4) is compatible with the input forms for most of the simulators available for process analysis and design. Many authors used alternative forms to estimate the interaction parameters but those forms are not supported by the simulation platforms making slow the process development and inflexible.
2.2.1.2 UNIQUAC
The UNIQUAC model was also considered in this study due to its high accuracy for thermodynamic modeling of nonideal systems. This model is a so-called lattice model and has been derived from a first order approximation of interacting molecule surfaces in statistical thermodynamics, this study considered the form of the model for binary systems [9].
Equations [5] and [6] allow the calculation of the activity coefficients for the two components in the mixture:
Here r, q and q' are parameters related to each pure component involved in the system. li, θi, θi' and are calculated using the equations (7), (8), (9) and (10).
2.2.2 Equations of state, constants and parameters
The detailed modeling of all the properties involved in the VLE requires of EPS (equations of state) to consider in detail the non-ideal behavior of the ethanol water-system. In order to quantitative describe the vapor phase the Polar Fluid Soave-Redlich-Kwong Equation of State (polar-SRK) [10] EPS is used.
2.2.2.1 Polar Fluid Soave-Redlich-Kwong Equation of State (polar-SRK)
The four parameters extension of the SRK EPS to reproduce the properties of polar fluids is presents in equation (11), in an explicit form for pressure. This equation of state requires two additional empirical parameters to be implemented (m and n), these parameters for the two substances involved in the study are presents in the Table 2.
2.2.2.2 Rackett equation
The implementation of the Rackett equation for the accurate estimation of the molar volume of the components in liquid as function of the temperature allows to improve the accuracy of the results obtained.
This is because the condition is isobaric for the thermodynamic modeling and the main effect over the density of the liquids is due to the equilibrium temperature, this EPS take in to account the change of the liquid density as a function of the temperature, in terms of reduced temperature (Tr) in a simple way.
The implementation of the Rackett equation implies the use of the fluid properties at critical conditions, for the system under study the critical constants are presents in the Table 2.
2.2.2.3 Antoine equation
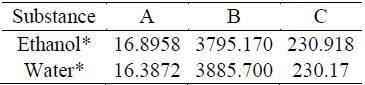
In the VLE calculations the prediction of the saturation pressures (Psat) has great effects on the results, in order to estimate properly this properties the Antoine equation (15) was used[11]
The Antoine equation requires for its use at least 3 empirical constants, for the ethanol water system these constants are presented in the Table 3.
2.3. Regression approach
The data regression was developed with the Maximum likelihood method. The P.F. (objective function) minimized for the adjustment of the parameters was the equation (16):
Table 1 NRTL binary interaction parameters, standard parameters [13], [14] and low pressure parameters.
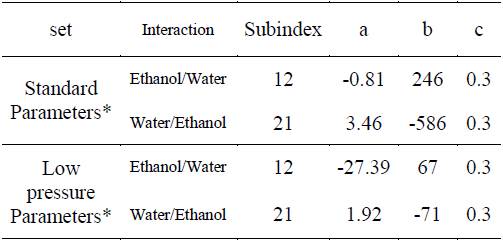
*The range of temperature recommended to use these parameters is from 298.14 to 373.15 K.
Table 2 UNIQUAC binary interaction parameters, standard parameters (13), (14) and low pressure parameters.
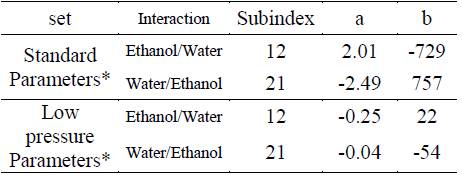
*The range of temperature recommended to use these parameters is from 298.14 to 373.15 K.
Table 3 UNIQUAC pure substances parameters for ethanol and water [15].

*The range of temperature recommended to use these parameters is from 298.14 to 373.15 K.
It should be noted that a is the standard deviation in the determination of each property, for bubble point calculations their value is adjusted to 0.1 as was recommended by E.C. Voutsas, et al [6].
2.4. VLE definition
The VLE approach used for the modeling is the γ-φ formulation [10], where φ is the fugacity coefficient for the vapor phase non-ideality estimation. In this case the formulation was implemented using the detailed modeling of the VLE and solved numerically with Python 3.4® scripts. This approach allows to calculate dew point and bubble point based in the mathematical models summarized above in a more accurate way than the typical one, even when the algorithm is essentially the same described by Smit & et al [11].
3. Results and Discussion
3.1 Thermodynamic consistency
The consistency of the experimental data used for the regression of the new binary interaction parameters was tested using the Redlich-Kister area-test method. This is the suitable way to assess the consistency of the thermodynamic data for systems with interactions that cause non-ideal behavior in the VLE [12]. The results of the consistency test performed using this method are summarized in the Table 4.
The experimental data is thermodynamically consistent, using the area test we realize that the data for the pressure of 19.71 kPa presents the lowest consistency, and the pressure of 13.15 kPa presents the highest consistency. Taking as a criteria of successful consistency 10% of tolerance the three datasets passed the test, being the lowest pressure the more consistent dataset. The consistency test allows to establish that the experimental data can be used for interaction parameters regression.
3.2 Binary interaction parameters for low pressures
Using the regression approach mentioned and the experimental data presented in Table 1, the binary interaction parameters was regressed for the two activity models, NRTL and UNIQUAC. The binary interaction parameters for the ethanol-water system are adjusted to be used in the form of the equation (4), such form of the temperature dependency is compatible with most of the commercial simulators used by process engineers in the design and rating of separation units for ethanol.
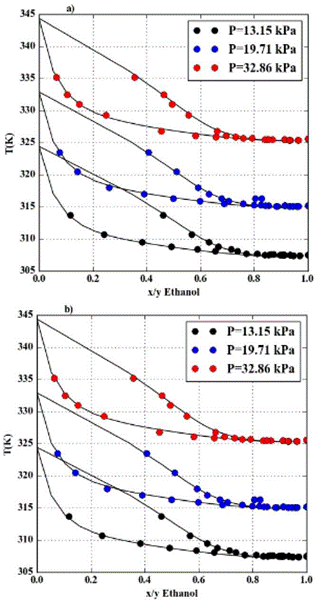
Figure 1 Thermodynamic modeling results (this study) and experimental data (6) for: a) NRTL and b) UNIQUAC at 3 low pressures (13.15, 19.71 and 32.86 kPa).
The binary interaction parameters adjusted for the NRTL model are presented in the Table 5, and the binary interaction parameters for the UNIQUAC model are presented in the Table 6.
3.3 Phase Equilibria - NRTL and UNIQUAC
Implementing the two models mentioned (NRTL and UNIQUAC), the binary interaction parameters regressed from the experimental data collected and the EPS for liquid volumes, saturation pressures and vapor phase behavior, the mathematical-thermodynamic modeling of the ethanol-water system were developed.
The Figure 1 shows the results for 3 low pressures (13.15, 19.71 and 32.86 kPa) and the points corresponding to the experimental data at those pressures using the two activity models with the new binary interaction parameters. Here it can also be seen that the experimental data is accurately represented with both models, NRTL and UNIQUAC. This behavior at low pressures is of importance for the development of chemical processes involving the VLE for the ethanol-water system.
Figure 2 shows the dispersion of the results for the VLE thermodynamic modeling using NRTL and UNIQUAC proposed parameters. The results in the Figure 2 are the Bubble temperature and the vapor composition as molar fraction calculated using the python 3.4® codes for the VLE modeling with the new binary interaction parameters.
The variables plotted for the 3 under-atmospheric pressures in the Figure 2 presents low dispersion, this analysis was not developed for the VLE estimations presented by E.C. Voutsas, et al [6] in 2011 when they proposed a quadratic form for the binary interaction parameters estimations. To validate the binary interaction parameters proposed in this study a correlation analysis was developed, the Table 8 contains the results for the analysis of the variables involved in the VLE calculations mentioned. The values for the correlation coefficient (R2) are almost 1, which means there is a good quantitative representation of the thermodynamic behavior of the binary mixture VLE. The P-Value values calculated are very low, that is coherent with the results of the thermodynamic consistency test developed for the experimental data.
3.4 Azeotropic Point Prediction
The ethanol-water system is a non-ideal binary mixture that means the representation of the VLE is dominated mostly by the azeotropic point. To validate the reliability of the new binary interaction parameters, and the thermodynamic modeling proposed, at under-atmospheric pressures, 17 experimental azeotropic points were considered at 17 different pressure values [6].
For each of the 17 experimental azeotropic points the VLE calculations, using the new parameters and modeling approach, were developed with the Python 3.4® codes, and the results compared directly with the experimental data, the results obtained are summarized in ¡Error! No se encuentra el origen de la referencia..
The results allows estimating the azeotropic point with error of less than 1%.
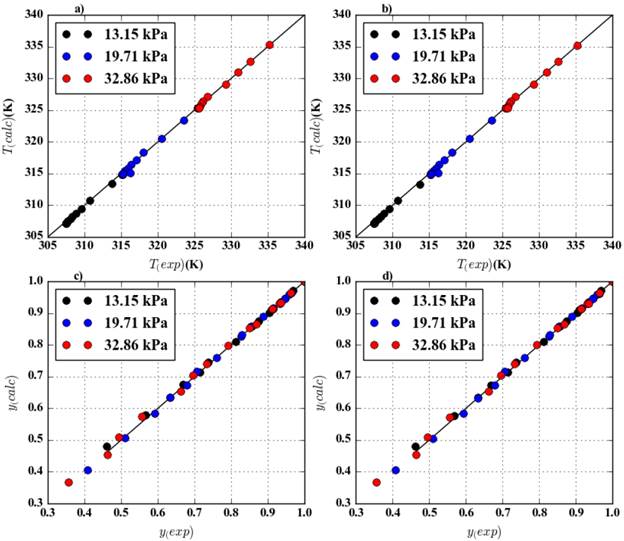
Figure 2 Thermodynamic modeling dispersion analysis for 13.15 kPa, 19.71 kPa and 32.85 kPa using python 3.4® codes: a) Temperature calculated using NRTL, b) Temperature calculated using UNIQUAC, c) Ethanol vapor phase molar fraction calculated using NRTL and d) Ethanol vapor phase molar fraction calculated using UNIQUAC.
Table 8 Correlation parameters (R2 and P-Value) for the thermodynamic modeling of the ethanol-water VLE using NRTL and UNIQUAC new binary interaction parameters for low pressure at 13.15 kPa, 19.71 kPa and 32.85 kPa.
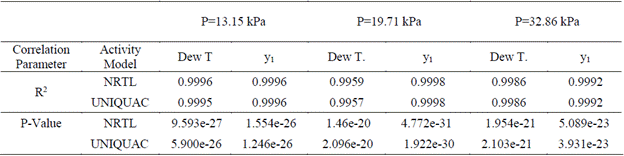
Table 9 Azeotropic point prediction error with NRTL and UNIQUAC new low pressure binary interaction parameters.
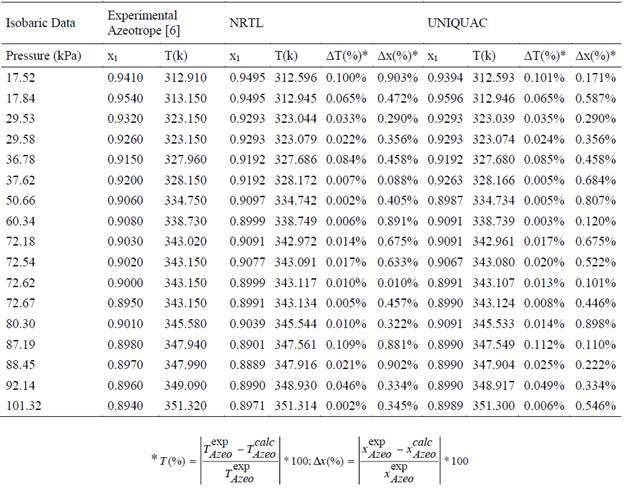
The UNIQUAC model is more accurate than NRTL, the highest error for the liquid composition of ethanol in molar fraction using NRTL is 0.903%, using UNIQUAC the highest error for the same variable is 0.898% in terms of temperature the highest error is 0.112% obtained with UNIQUAC and the highest error with NRTL is 0.109%.
The mean error for NRTL for the variable temperature is 0.033% and for the liquid composition of ethanol in molar fraction the mean error is 0.495%.
For the UNIQUAC model the mean error for temperature is 0.034% meanwhile for composition of ethanol in liquid phase in molar fraction the mean is 0.431%.
Considering this results for the azeotropic point prediction the NRTL model is more accurate than the UNIQUAC model for the bubble point representation. In the case of liquid phase composition in molar fraction the error is slower using the UNIQUAC model.
4. Conclusions
This study examined the mathematical-thermodynamic modeling of the ethanol-water system using experimental data at 3 different under-atmospheric pressures for VLE, and 17 azeotropic point data, to regress new and more accurate binary interaction parameters.
The parameters were adjusted for two excess Gibbs energy models (NRTL and UNIQUAC), and are presented in a simple temperature dependency form compatible with most of the process simulators available, and commonly used for chemical processes design and rating.
The use of these parameters will help the engineers and scientists in the development of new technologies for ethanol-water separation, and in the improvement of conventional technologies actually implemented.
The thermodynamic consistency test of Redlich-Kister based on areas difference was implemented to test the experimental data collected and presented in this study, aiming to provide reliable data set for future developments in the field.
Detailed mathematical-thermodynamic modeling was developed using python 3.4® codes and high computation power. The approach performed was the most rigorous, considering model for all the VLE variables in order to avoid ideal assumptions: vapor phase was considered using the polar-SRK EOS, Antoine and Rackett Equations for saturation pressures and liquid densities respectively. The results were compared with the experimental data at 3 different under-atmospheric pressures (13.15, 19.71 and 32.86 kPa) for the two activity models (NRTL and UNIQUAC), and using the new adjusted binary interaction parameters. The correlation coefficients calculated to validate the modeling are close to 1with both models. P-values calculated for the VLE are lower of 1x10-5 in all cases supporting the validity of the thermodynamic modeling results.
To consider the azeotropic point estimation at low pressures in detail, the experimental azeotropic data for 17 different pressure values were used to evaluate the accuracy of the thermodynamic modeling approach using NRTL and UNIQUAC with the new proposed binary interaction parameters through the python 3.4® codes provided by S&SE S.A.S. in all cases the error is lower than 1%, meaning that the approach proposed and the parameters regressed have a high accuracy. For the bubble temperature the mean error is smaller than 0.034% and for the liquid phase composition of ethanol in molar fraction the mean error is in both cases smaller than 0.495%, which validates the capabilities of the models and the new parameters proposed to reproduce quantitatively the behavior of the non-ideal binary system of ethanol-water.
The thermodynamic model presented in this study can be fully implemented in parallel with CFD (computational fluid dynamics) simulations to consider the detailed thermodynamic behavior in a coupled way with the transport phenomena, a very recent field of research due to its technical possibilities.