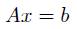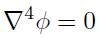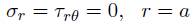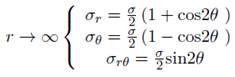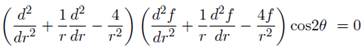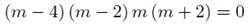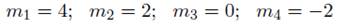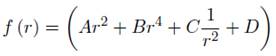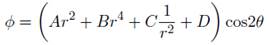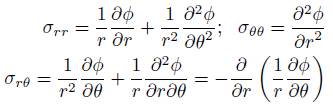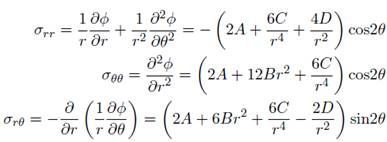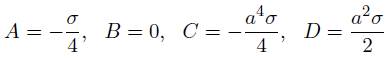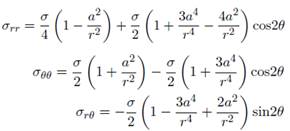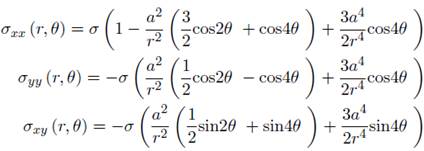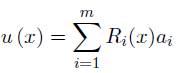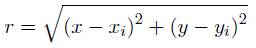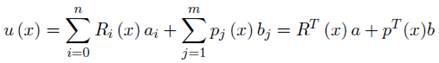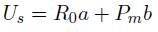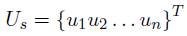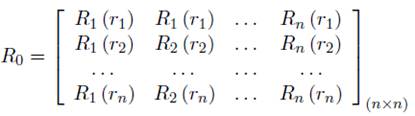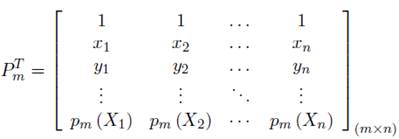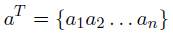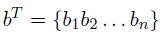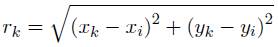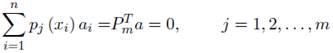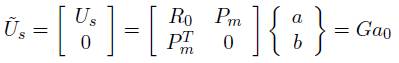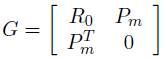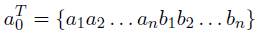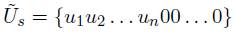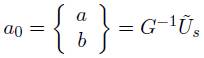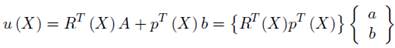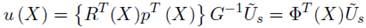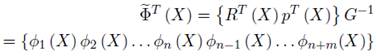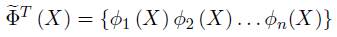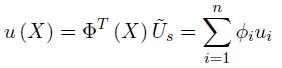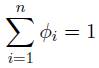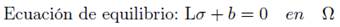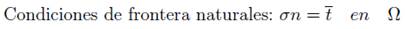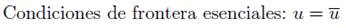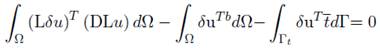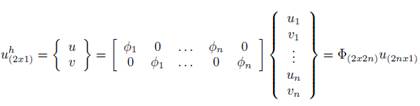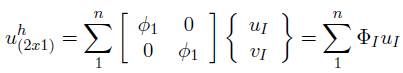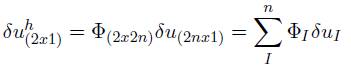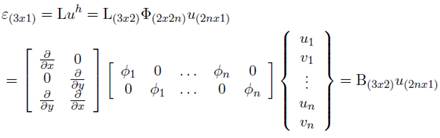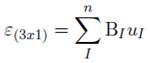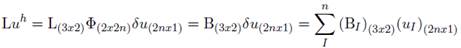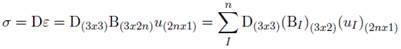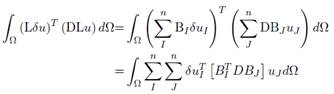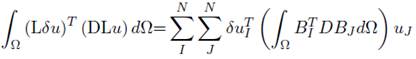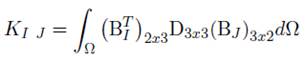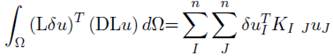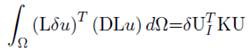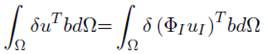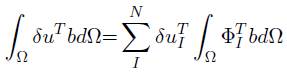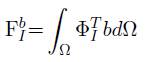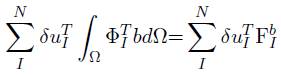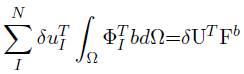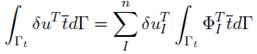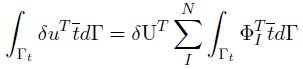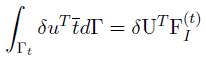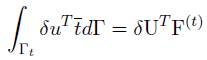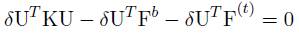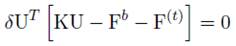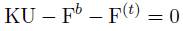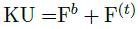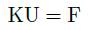1 Introducción
La necesidad de resolver problemas mucho más complejos en la actualidad ha producido la búsqueda de nuevas herramientas numéricas que permitan ser más eficientes y fáciles de manejar. La técnica más utilizada ha sido los elementos finitos o FEM siendo una de las técnicas más consolidadas y con mucha más robustez, a pesar de esto esta técnica no deja de tener inconvenientes, entre ellos encontramos la etapa de pre procesador, encar- gado de genera una malla sobre el dominio de trabajo. Dependiendo del problema y la geometría este debe hacerse con un mayor refinamiento lo que se traduce en tiempo prudente de maquina sobre todo en estructuras complejas, haciendo que la técnica numérica sea más lenta en el proceso.
El desarrollo de los métodos MFree se remonta a más de 30 años donde Slater en 1934 1, Jones et al. en 1937 2 y Lanczos en 1938 3, dieron a conocer el método de puntos de colocación. Entre los primeros métodos MFree se encuentran el método de vórtice, dados a conocer por Chorin en 1973 4 y Bernard en 1995 5. Así como las diferencias finitas con redes arbitrarias o llamadas (GFDM) mostradas por Giralut en 1974 6 y Pavlin et al. en 1975 7, Vesey et al. en 1981 8, Liszka et al. en 1977 9 y Krok et al. en 1989 10 fueron una de las primeras técnicas libres de malla implementadas.
Uno de los métodos más conocidos es llamado dinámica de partículas (SPH), el cual fue utilizado para modelado de fenómenos astrofísicos como son la explosión de estrellas y nubes de polvo, los cuales no tenía límites y sus fronteras se extendían a lo largo de años luz. La mayoría de los trabajos de investigación anteriores sobre SPH se refleja en las primeras publicaciones de Lucy en 1977 11 y Monaghan et al. en 1985 12, luego en 1992 sobre la misma línea de investigación Gingold et al.13 aplican el método numérico como herramienta de solución a las ecuaciones que modelan las explosiones de supernovas y estrellas. Desarrollos recientes del método (SPH) con nuevas fundamentaciones se pueden encontrar en artículos publicados por Liu en el año 2003 14.
En 1990, un grupo de métodos MFree han sido desarrollados en gran medida, entre estos tenemos los denominados métodos de elementos difusos (DEM) propuestos por Touzot en 1992 15. El método de Free Galerkin (EFG) propuesto por Lu et al. en 1994 16, el método de reproducción de partículas (RKMP) propuesto por Jun et al.17, el método de los puntos de interpolación propuestos por Liu et al.18, el método sin malla de Petrov-Galerkin (MLPG) propuesto por Atluri et al.19, el método de nodos de frontera (BNM) expuestos por Mukherjee 20, el método de interpolación de puntos límites (BPIM) por Liu y Gu 21,22, MeshFree fuertes y débiles (MWS) propuestos por Liu y Gu 23. Donde las funciones de aproximación se construyen mediante un conjunto de nodos arbitrarios, y ningún elemento o conectividad de los nodos se hace necesario para la aproximación de dichas funciones.
A pesar de que han existido muchas técnicas libres de malla no fue hasta hace dos décadas que este tipo de método se dio a conocer con más fuerza, realmente el primer método propuesto formalmente fue dado a conocer por Lu et al. en 1994 16 denominado Free Galerkin. Actualmente es uno de los mayores exponentes y diseñador de su propia técnica. Liu 14 en el 2003 realiza una publicación de todos sus trabajos realizados hasta el momento, donde da a conocer la nueva técnica que consta de la no utilización de mallas para el dominio de soporte. Esta se basa simplemente a una distribución aleatoria de puntos o nodos sobre el dominio y es aquí donde la técnica empieza a ser acogida puesto que el tiempo invertido en la generación de mallas se convierte en tiempo utilizado para resolver el problema planteado.
Todas las técnicas deben solucionar de manera eficiente la expresión (1), debido a que los problemas son traducidos a sistemas de ecuaciones algebraicas la solución se obtiene desarrollando la siguiente expresión:
La solución de la ecuación (1) depende de la buena escogencia del dominio de soporte como de los monomios de la base en la función RPIM. La adición de polinomios en la base del método MFree garantiza que siempre la matriz A sea no singular, la aplicación de una definición tan sencilla como el rango de una matriz permite definir si A es singular, lo que indica intrínsecamente el aporte que generan los nodos en la función de forma.
2 La solución analítica
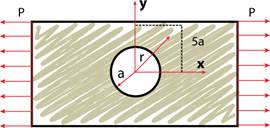
El problema de Kirsch consiste en una placa infinita sometida a un esfuerzo uniaxial T con un agujero centrado de radio a como lo muestra la Figura 1, para obtener la solución a este problema se hace necesario recurrir a la ecuación diferencial general de la teoría de placas (2), 24.
Para la solución de este problema es posible considerar una parte del plato debido a la simetría que se presenta con respecto al eje y, para empezar con la solución de este problema se deben establecer las siguientes condiciones de frontera en cuanto a los esfuerzos 25.
Dada las anteriores condiciones se desarrollará la ecuación diferencial biarmónica (2), cambiando φ = f (r)cos2θ y reemplazando éste valor en la ecuación anteriormente descrita se tiene una ecuación diferencial ordinaria, para la determinación de f (r) se tiene que:
La solución de f (r) = Crm , por lo que resulta la siguiente ecuación para m.
Las cuatro raíces que satisfacen la ecuación son:
Por tanto la solución para f (r) viene dada por:
La función φ queda reescrita como:
Dada la ecuación de esfuerzo en coordenadas polares descritas como:
Reemplazando (9) en la ecuación (10) tenemos:
Al evaluar las condiciones de frontera es posible determinar el valor de los coeficientes dando como resultado 25:
Sustituyendo estos valores en (11) se tiene que:
Organizando la relación (13) se obtiene la solución de forma polar para la obtención de los esfuerzos generales del problema de Kirsch;
3 Las funciones de interpolación de bases radiales
Teniendo en cuenta la definición de una función de interpolación, la función de interpolación en función de una base radial se puede escribir como:
La función de base radial Ri (x) es la distancia que existe entre el punto de interés x y un nodo xi dentro de un dominio de soporte.
Las RBF más típicas son:
dc es una característica del espaciamiento del dominio de soporte local con respecto al punto de interés x.
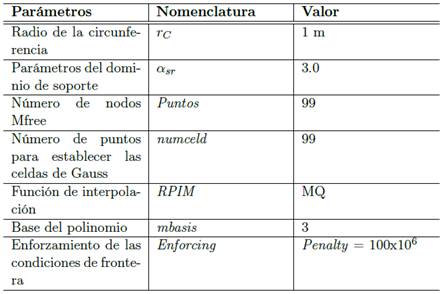
Los parámetros de forma en la Tabla 1 son valores determinados por el comportamiento de la solución. Aunque son un caso de estudio en la actualidad, existen algunos parámetros estándar dependiendo del enfoque del problema, si está relacionado con la mecánica de sólidos o con fluidos, estos parámetros de forma son establecidos en trabajos realizados por Liu (26), cuyos valores son mostrados en las Tablas 2 y 3, para cada una de las funciones de forma.
Tabla 2: Parámetros de la función radial MQ (αc, dc, q), parámetros del dominio de soporte (αsx, dc).
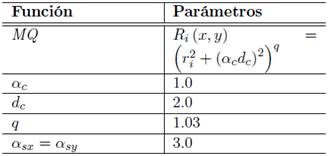
Tabla 3: Parámetros de la función radial EXP (αc, dc, ), parámetros del dominio de soporte (αsx, dc). 
Teniendo en cuenta estos parámetros, las funciones de base radial puras, como las presentadas en la Tabla 1, dentro de los elementos libres de malla, no siempre cumplen con la reconstrucción exacta de un polinomio lineal, teniendo como consecuencia la singularidad de la matriz de momentos, debido a esto se hace necesario adicionar polinomios que permitan cumplir con dicha condición esencial para el método sin malla, sin necesidad de producir efectos adversos sobre el desempeño de dicha función de forma. Estos polinomios adicionales son tomados del triángulo de pascal y son llamados polinomios base y tienen la capacidad de garantizar que dicha matriz de momentos sea invertible. A parte de mejorar la estabilidad de interpolación al momento de obtener dicha matriz (27).
3.1 La función de forma RPIM
De acuerdo a Liu (26) la función de interpolación RBF con polinomios adicionales puede ser escrita como:
Donde Ri (x) es una función de base radial (RBF), n es el número de RBFs, pj (x) es un monomio en el espacio coordenado xT = (x, y), y m es el número de polinomio base utilizados, para un caso 2D si m = 3, pT (x) = pT (x, y) = 1, x, y, cuando m = 0 la ecuación
(17) se convierte en una RBFs completamente pura. Los coeficientes ai y bj son constantes que deben ser determinados dependiendo de la base es- cogida en el dominio 3 (generalmente el valor de la base tiene un coeficiente m = 3 para un problema bidimensional).
La ecuación (17) debe satisfacer los n nodos alrededor del punto de interés x, lo que implica que deben haber n ecuaciones lineales, una por cada nodo, se puede por tanto expresar estas ecuaciones de forma matricial como:
Donde el vector de valores Us de desplazamiento es:
La matriz de momentos RBFs es:
La matriz de momentos polinomial.
El vector de coeficientes para RBFs es:
El vector de coeficientes para los polinomios es:
Por otro lado rk en Ri (rk) está definido como
Debido a que existen m + n variables en la ecuación (18). La adición de m ecuaciones solo puede ser adicionada si se tiene en cuenta la siguiente consideración:
Al combinar las ecuaciones (18) y (25) tenemos como resultado la ex- presión matricial:
Donde
Debido a que la matriz R0 es simétrica, la matriz tt debe ser también simétrica, solucionando (26) tenemos:
Reescribiendo (17)
Reemplazando (30) en (31)
Donde la función de forma RPIM puede ser expresada como
Finalmente la función de forma correspondiente al espaciamiento nodal es el vector ΦT (X) que está definido como:
La ecuación (31) puede ser finalmente reescrita como:
RPIM tiene la propiedad de partición unitaria la cual es demostrada por Gr. Liu (14), por tanto
Esta representación será utilizada como función de forma dentro de la discretización de la formulación variacional.
4 La Formulación
Al considerar un problema de elasticidad lineal en un espacio R2, se encuen- tra definido un dominio Ω con condiciones de frontera Γ cuyas ecuaciones se encuentran descritas como,
Donde:
L: operador diferencial.
b: vector de esfuerzo externo al cuerpo. σ = {σxx σyy τxy}: Vector de esfuerzos.
uT = {u v}: Vector de desplazamientos.
t: Tracción en las condiciones de frontera naturales.
u: Desplazamiento en las condiciones de frontera esenciales.
n: vector unitario normal a la condición de frontera natural.
La forma variacional estándar para la ecuación (37) es planteada de la siguiente manera:
La ecuación (40) está definida para un problema de dominio global Ω, donde D es la matriz de constantes del material (D esfuerzo o deformación plana). El primer término de la expresión es el trabajo virtual dado por el esfuerzo interno en el dominio Ω, el segundo término es el trabajo virtual por las fuerzas externas en Ω y el tercer término corresponde al trabajo virtual hecho por la tracción externa en la frontera Γt.
Por otro lado, la aproximación de los desplazamientos sobre cualquier punto de interés, usando un conjunto de nodos en un subdominio de soporte local con respecto a un punto es:
La cual puede reescribirse como (42) como el aporte de cada subdominio local.
Donde ΦI es la matriz de funciones de forma RPIM del nodo I mediante las funciones radiales de interpolación, y uI es el desplazamiento nodal del nodo I.
En la ecuación (41), uT es la aproximación de los desplazamientos de un punto de interés, el cual es un punto de evaluación dentro de la cuadratura (Cuadratura de Gauss).
Teniendo en cuenta que la formulación débil parte del principio del trabajo virtual dada por la expresión (40), de la expresión (42), el despla- zamiento virtual se obtiene al multiplicar la expresión por δ.
IEs preciso calcular la deformación en función de los desplazamientos para esto se tiene que:
Expresado como:
Donde B es la y BI es la matriz de deformación de nodo I.
De la misma manera,
Ahora se obtiene el vector de esfuerzos usando las ecuaciones constitutivas en un punto del dominio Ω. La ecuación (46) debe satisfacer los n nodos al rededor del punto de interés x, lo que implica que deben haber n ecuaciones lineales, una por cada nodo, podemos por tanto expresar estas ecuaciones de forma matricial.
Sustituyendo (45) y (46) dentro del primer término de (40), la expresión queda descrita como:
Reescribiendo la ecuación (48):
KI J es llamada matriz de rigidez, donde I y J corresponde al punto de integración de la cuadratura del dominio de soporte, la ecuación (48) puede reescribirse como:
Finalmente (49) pude escribirse como la ecuación (51) la cual debe satisfacer los n nodos al rededor del punto de interés x, lo que implica que deben haber n ecuaciones lineales, una por cada nodo, podemos por tanto expresar estas ecuaciones de forma matricial.
Para el segundo término de la ecuación (40), podemos reemplazar (42).
Fb es el vector de fuerza del campo del nodo I, y b vector de fuerza de cuerpo del nodo I, la ecuación (53) puede reescribirse.
Donde Fb el vector de fuerza de cuerpo global, UT vector de desplaza- mientos global.
Para el tercer y último término el procedimiento es exactamente igual. Con la excepción que las fuerzas de cuerpo son reemplazadas por el vector de tracción y el dominio de integración se hacen sobre la frontera, de esta manera la expresión obtenida es:
F( t ) el vector de tracción de I-ésimo nodo. De forma general
Donde F( t ) es el vector de tracción global.
Ya obtenidas las ecuaciones discretas se reescribe la ecuación (40) en función de las ecuaciones (52),(57) y (61).
Factorizando,
La ecuación (63) puede ser satisfecha, ya que δU T es arbitrario.
O reescrita como:
Reemplazando F b + F( t ) por F, tenemos que:
La ecuación (66) es la representación discreta del sistema de ecuaciones para RPIM Mfree de 13, llamada como formulación débil para la solución del problema de Kirsch.
5 Resultados
Antes de desarrollar el problema de Kirsch mediante métodos numéricos mencionados, obtendremos el comportamiento de la solución analítica del problema mediante las ecuaciones planteadas, dichas gráficas y resultados serán tomados como referencia para hacer la comparación de la solucion numérica del problema.
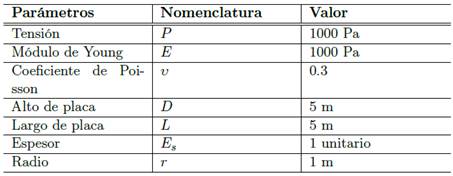
Se parte por establecer los parámetros de entrada a nuestro problema (Tabla 4) y las condiciones de frontera dadas por (3).
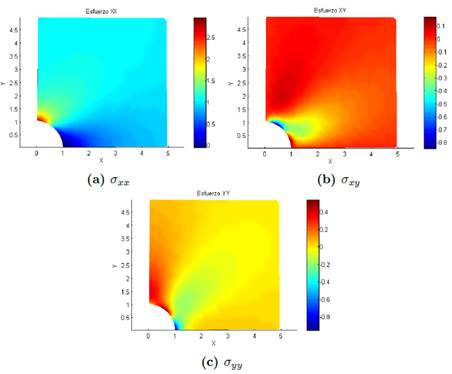
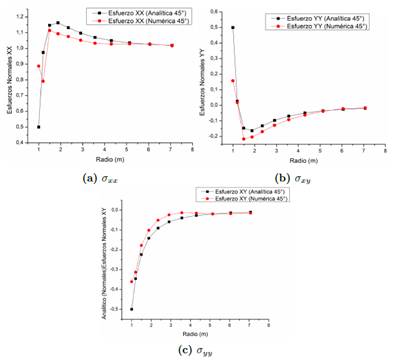
Los esfuerzos σxx , σxy y σyy calculados con las expresiones (14) y los parámetros de entrada de la Tabla 4, se muestran en la Figura 2.
Los valores numéricos obtenidos por la solución analítica del problema y representados en la Figura 2, serán tomados como referencia de la precisión del método numérico implementado.
Ahora se debe definir los parámetros de entrada correspondientes al método numérico RPIM, estos parámetros se consignan a en la Tabla 5.
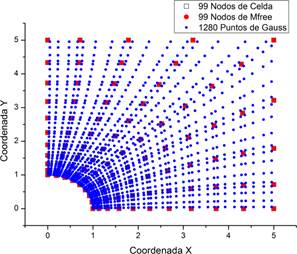
A partir de esta información se determina la nube de puntos MFree sobre el dominio, para este análisis tomaremos una distribución radial de forma regular.
Tomando la referencia de la Tabla 5 la malla resultante se muestra en la Figura 3.
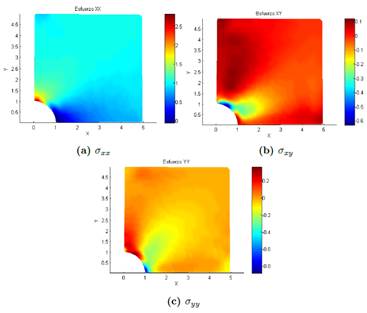
Al aplicar el algoritmo RPIM con la función de forma MQ sobre la malla de la Figura 3 las soluciones de los esfuerzos obtenidos son mostrados en la Figura 4.
Se observa que visualmente las figuras de contorno mostradas en 4, son muy similares a las figuras de la solución analítica presentadas por la Figura 2, esto muestra una mejora en la apreciación visual del problema sin embargo no se muestra qué tan preciso es el método numérico aplicado al problema de Kirsch, si no que se necesita un valor cuantitativo que indique dicha desviación. Se toma el punto medio como punto de evaluación a un ángulo de θ = 45 como referencia puntual.
Los esfuerzos obtenidos por el método RPIM (MQ ) mostrados en la Figura 5 indican una excelente aproximación a la solución analítica del problema, las figuras de contorno (Figura 4) del método numérico es similar a la solución real, sin embargo, quien define la precisión de la función de interpolación utilizada es la medición del error.
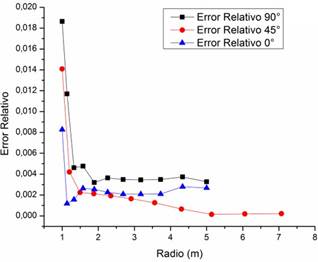
El error y el error relativo mostrado en la Tabla 6 es muy bajo en función del principio de mínima energía, dicha relación permite determinar que el método numérico es muy preciso en la interpolación de la solución, por tanto, la propagación del error sobre los puntos de interés deben disminuir, los errores relativos graficados en función del radio son indicados por la Figura 6.
Tabla 6: Cálculo del principio de mínima energía, error relativo y Error relativo normal, para la función MQ de RPIM.

Como se observa en la Figura 6 el error en función del radio disminuye tendiendo a cero lo que indica que el método numérico se acerca de manera precisa a la solución analítica del problema al evaluar el error en diferentes ángulos mostrando una alta confiabilidad en el método numérico como metodología para el desarrollo simulaciones mecánicas.
5 Conclusiones
La ventaja en el cálculo de las funciones de forma de los elementos libres de malla (Mfree) con respecto a la técnica FEM sin duda es uno de los más grandes avances dentro de las técnicas de cálculo numérico, ya que MFree no depende del desarrollo de un mallado estructurado con el propósito de obtener las conectividades de los elementos, si no que permite colocar puntos aleatorios para la obtención de la función de forma. Una de las grandes ventajas del método numérico es la no utilización de mallas sobre el dominio, en cambio se deben utilizar nodos distribuidos sobre el dominio, disminuyendo el tiempo de pre-procesamiento, lo único que debe tener en cuenta es la cantidad de nodos y el distanciamiento nodal sobre el dominio de interpolación.
Cabe resaltar la utilización de los polinomios base para garantizar la invertibilidad de la matriz de momentos, si dicha base no es tomada ade- cuadamente la matriz de momentos es no invertible por lo que el sistema no tendría una solución.
Los indicadores del error muestran la aproximación cercana entre el método numérico y analítico lo que permite mostrar que los MFree son una muy buena técnica para la simulación y solución de muchos problemas no solo en la mecánica de solidos si no en otras áreas de ingeniería. Los erro- res de redondeo y de aproximación se hacen inherentes a las operaciones realizadas, esta inestabilidad es apreciada cuando se hace una normaliza- ción del dominio lo cual influye sobre todo en el cálculo de las matrices de momentos y de su inversa.
La velocidad del método numérico RPIM en la etapa del procesador depende de la cantidad de operaciones que la función radial debe hacer para calcular la función de forma por cada subdominio correspondiente a cada punto de evaluación.
Aunque el método es llamado libre de malla se debe considerar la dis- tancia en la distribución nodal de los nodos de campo, esta distancia es fundamental en la solución ya que al no considerar esta restricción el mé- todo numérico tiene un mal comportamiento en la solución del problema.
El método numérico no está tan formalizado como sus antecesores FEM, CFD y DF por lo que se hace necesario seguir trabajando sobre la for- mulación del método sobre el forzamiento de las condiciones de frontera naturales y las esenciales.