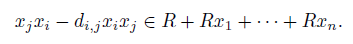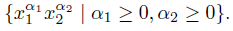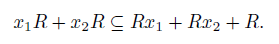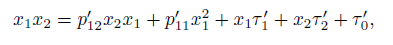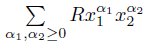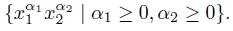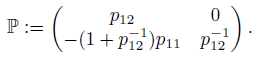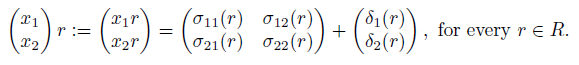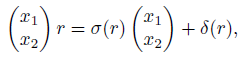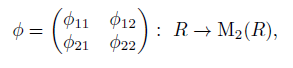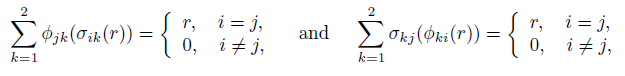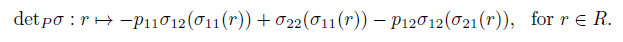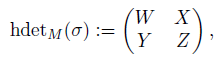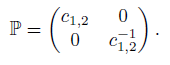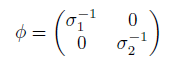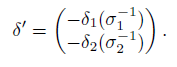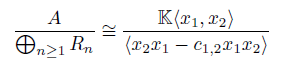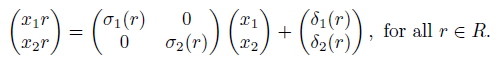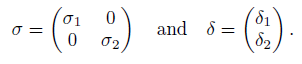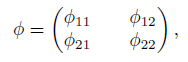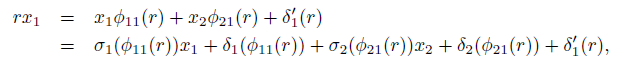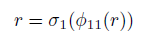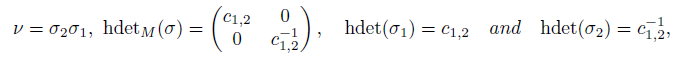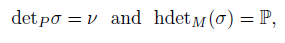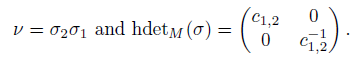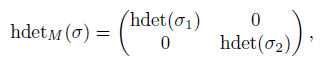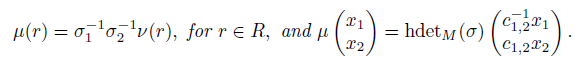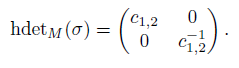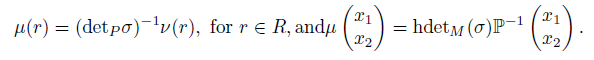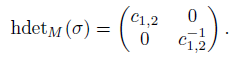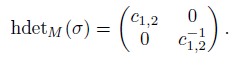1. Introduction
In [16] the homological determinant was defined and used to study the Artin-Schelter regular property of some algebras. Shen et al., [34] and Wu et al., [41] gave equivalent definitions of the homological determinant and established connections between homological determinant and the usual determinant. On the other hand, Nakayama automorphism plays an important role in noncommutative algebraic geometry (see Reyes et al., [27]) and its computation is not easy in the general case. Some authors have computed and studied this automorphism for special types of algebras, see for example [22, 23, 24, 27, 33, 34, 39, 45]. The remarkable fact is the relationship between both notions, see Reyes et al., [27], Shen et al., [34] and Zhun et al., [45], for more details. Double Ore extensions, denoted by A = RP [x1, x2; σ, δ, τ ], were defined by Zhang and Zhang [43] where they proved that a connected graded double Ore extension of an ArtinSchelter regular algebra is Artin-Schelter regular. Later, in [44], they constructed 26 families of Artin-Schelter regular algebras of global dimension four by using double Ore extensions. For R a Koszul Artin-Schelter regular algebra, Zhun et al., [45] calculated the Nakayama automorphism of a trimmed double Ore extension RP [x1, x2; σ], and the Nakayama automorphism of an iterated skew polynomial extension of a Koszul ArtinSchelter regular algebra by using the homological determinant. Another properties of double Ore extensions have been explored by Carvalho et al., [6] and Zhun et al., [45].
Now, for A = RP [x1, x2; σ, δ, τ ] a right double Ore extension, Zhang and Zhang [43] introduced the 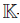 -linear map det Pσ : R → R of σ called the P-determinant. This Pdeterminant was used to prove the Artin-Schelter regular property of double Ore extensions. Zhun et al., [45] used the P-determinant to calculate the Nakayama automorphism of certain algebras. For the case where R is a Koszul Artin-Schelter regular algebra and σ : R → M2(R) is an algebra homomorphism, Zhu et al., [45] defined the homological determinant of σ, denoted by hdetM, and presented some connections between the Nakayama automorphism, the homological determinant, and the P-determinant. These authors used the homological determinant of σ to know when a trimmed double Ore extension of a Koszul Artin-Schelter regular algebra turns out to be Calabi-Yau.
-linear map det Pσ : R → R of σ called the P-determinant. This Pdeterminant was used to prove the Artin-Schelter regular property of double Ore extensions. Zhun et al., [45] used the P-determinant to calculate the Nakayama automorphism of certain algebras. For the case where R is a Koszul Artin-Schelter regular algebra and σ : R → M2(R) is an algebra homomorphism, Zhu et al., [45] defined the homological determinant of σ, denoted by hdetM, and presented some connections between the Nakayama automorphism, the homological determinant, and the P-determinant. These authors used the homological determinant of σ to know when a trimmed double Ore extension of a Koszul Artin-Schelter regular algebra turns out to be Calabi-Yau.
The noncommutative rings of polynomial type of interest in this paper are the skew P BW extensions, denoted by A = σ(R){x1, . . . , xn}, which were defined by Gallego and Lezama [8] with the aim of generalizing another families of noncommutative rings appearing in several branches of mathematics (c.f. Bell and Goodearl [5] and Ore [25]). These objects have been recently studied (e.g., [1, 2, 11, 12, 13, 17, 18, 19, 21, 40, 42]), and, as a matter of fact, a book containing some of the works developed for these objects has been published recently by Springer [7]. As a particular class of these objects, Suárez [35] defined graded skew P BW extensions over an  -graded algebra R and showed that if R is a finitely presented Koszul algebra, then every graded skew PBW extension over R is Koszul. The Artin-Schelter regular property and the skew Calabi-Yau condition for graded skew PBW extensions were studied by Suárez et al., [36]. There, the authors proved that every graded quasi-commutative skew PBW extension of an Artin-Schelter regular algebra is also Artin-Schelter regular; every graded quasi-commutative skew PBW extension over a connected skew Calabi-Yau algebra is skew Calabi-Yau; and every graded skew PBW extension over a connected Auslander regular algebras is Artin-Schelter regular and skew Calabi-Yau. With respect to the Nakayama automorphism, Suárez et al., [39] described it for A = σ(R) {x1, . . . , xn} by using the Nakayama automorphism of an Artin-Schelter regular algebra R, and also they calculated explicitly the Nakayama automorphism of some skew PBW extensions. About doble Ore extensions, Gómez and Suárez [9] gave necessary and sufficient conditions for a graded (trimmed) double Ore extension to be a graded (quasi-commutative) skew PBW extension. They proved that graded skew PBW extensions A = σ(R) {x1, x2} over Artin-Schelter regular algebras R are also ArtinSchelter regular, and graded skew PBW extensions A = σ(R){x1, x2} over connected skew Calabi-Yau algebras R of dimension d are skew Calabi-Yau of dimension d + 2.
-graded algebra R and showed that if R is a finitely presented Koszul algebra, then every graded skew PBW extension over R is Koszul. The Artin-Schelter regular property and the skew Calabi-Yau condition for graded skew PBW extensions were studied by Suárez et al., [36]. There, the authors proved that every graded quasi-commutative skew PBW extension of an Artin-Schelter regular algebra is also Artin-Schelter regular; every graded quasi-commutative skew PBW extension over a connected skew Calabi-Yau algebra is skew Calabi-Yau; and every graded skew PBW extension over a connected Auslander regular algebras is Artin-Schelter regular and skew Calabi-Yau. With respect to the Nakayama automorphism, Suárez et al., [39] described it for A = σ(R) {x1, . . . , xn} by using the Nakayama automorphism of an Artin-Schelter regular algebra R, and also they calculated explicitly the Nakayama automorphism of some skew PBW extensions. About doble Ore extensions, Gómez and Suárez [9] gave necessary and sufficient conditions for a graded (trimmed) double Ore extension to be a graded (quasi-commutative) skew PBW extension. They proved that graded skew PBW extensions A = σ(R) {x1, x2} over Artin-Schelter regular algebras R are also ArtinSchelter regular, and graded skew PBW extensions A = σ(R){x1, x2} over connected skew Calabi-Yau algebras R of dimension d are skew Calabi-Yau of dimension d + 2.
With all above results in mind, next, we present the structure of the article by mentioning the original results presented here. In Section 2, we present definitions and basic properties of ring theory and skew PBW extensions. In Section 3, we present some new results about these extensions. Briefly, Theorem 3.1 asserts that the Nakayama automorphism of a graded skew PBW extension A = σ(R){x1, . . . , xn} over a finitely presented Koszul Auslander-regular algebra R has trivial homological determinant. A particular case of this fact is presented in Corollary 3.2, where we show that the Nakayama automorphism of graded skew PBW extensions over the commutative polynomial ring R = 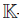 [t1, . . . , tm] is equal to 1. Now, since a graded skew PBW extension over a connected algebra R is a connected graded double Ore extension RP [x1, x2; σ, δ, τ ], in Theorem 3.4 we calculate the P-determinant of σ and the inverse of σ. In Theorem 3.5, for a quasi-commutative Calabi-Yau skew PBW extension A = σ(R){x1, x2} = RP [x1, x2; σ] over a Koszul ArtinSchelter regular algebra, we calculate the Nakayama automorphism of R and the homological determinant of σ in terms of the definition of skew PBW extension. In this sense, we also show the correlation between the Nakayama automorphism, the homological determinant and the homological determinant of σ. Finally in Corollary 3.6, we calculate the Nakayama automorphism of a graded quasi-commutative skew PBW extension A = σ(R){x1, x2} over a Koszul Artin-Schelter regular algebra R with Nakayama automorphism, and we establish a sufficient and necessary condition to guarantee that A is Calabi-Yau. In this way, this paper continues the research about Koszul, CalabiYau, Artin-Schelter and related ring theoretic notions for skew PBW extensions (c.f. [29, 36, 37, 38, 39]).
[t1, . . . , tm] is equal to 1. Now, since a graded skew PBW extension over a connected algebra R is a connected graded double Ore extension RP [x1, x2; σ, δ, τ ], in Theorem 3.4 we calculate the P-determinant of σ and the inverse of σ. In Theorem 3.5, for a quasi-commutative Calabi-Yau skew PBW extension A = σ(R){x1, x2} = RP [x1, x2; σ] over a Koszul ArtinSchelter regular algebra, we calculate the Nakayama automorphism of R and the homological determinant of σ in terms of the definition of skew PBW extension. In this sense, we also show the correlation between the Nakayama automorphism, the homological determinant and the homological determinant of σ. Finally in Corollary 3.6, we calculate the Nakayama automorphism of a graded quasi-commutative skew PBW extension A = σ(R){x1, x2} over a Koszul Artin-Schelter regular algebra R with Nakayama automorphism, and we establish a sufficient and necessary condition to guarantee that A is Calabi-Yau. In this way, this paper continues the research about Koszul, CalabiYau, Artin-Schelter and related ring theoretic notions for skew PBW extensions (c.f. [29, 36, 37, 38, 39]).
2. Preliminaries
Throughout the paper, the word ring means an associative ring with identity not necessarily commutative. If B is a ring, Mn(B) denotes the set of matrices of size n × n with entries in B. 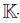 denotes a field; all algebras are
denotes a field; all algebras are -algebras. The symbol N will be used to denote the set of natural numbers including zero, and the tensor product ⊗ means ⊗K. An algebra B is
-algebras. The symbol N will be used to denote the set of natural numbers including zero, and the tensor product ⊗ means ⊗K. An algebra B is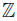 -graded, if there exists a family of subspaces {Bp}p∈Z of B such that B =
-graded, if there exists a family of subspaces {Bp}p∈Z of B such that B =  p∈Z Bp and BpBq ⊆ Bp+q, for all p, q ∈
p∈Z Bp and BpBq ⊆ Bp+q, for all p, q ∈  . A graded algebra B is called positively graded (or
. A graded algebra B is called positively graded (or -graded), if Bp = 0, for all p < 0. An
-graded), if Bp = 0, for all p < 0. An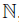 -graded algebra is called connected, if B0 =
-graded algebra is called connected, if B0 = 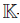 . A non-zero element x ∈ Bp is called a homogeneous element of B of degree p. If B =
. A non-zero element x ∈ Bp is called a homogeneous element of B of degree p. If B =  p∈Z Bp is a graded algebra,we set B(l) =
p∈Z Bp is a graded algebra,we set B(l) =  p∈Z B(l)p, where B(l)p = Bp+l , for l ∈
p∈Z B(l)p, where B(l)p = Bp+l , for l ∈  . An algebra B is finitely generated as
. An algebra B is finitely generated as 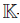 -algebra, if there exists a finite set of elements t1, . . . , tm ∈ B such that the set {ti1 ti2 · · ·tip | 1 ≤ ij ≤ m, p ≥ 1}∪ {1} spans B as a
-algebra, if there exists a finite set of elements t1, . . . , tm ∈ B such that the set {ti1 ti2 · · ·tip | 1 ≤ ij ≤ m, p ≥ 1}∪ {1} spans B as a 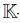 -space. For example the free associative algebra (tensor algebra) L in m generators t1, . . . , tm is denoted by L :=
-space. For example the free associative algebra (tensor algebra) L in m generators t1, . . . , tm is denoted by L :=  {t1, . . . , tm}. The degree (deg) of a word ti1 ti2 . . . tip is p; the degree of f ∈ L is the maximum of the degrees of the words in f. We include among the words a symbol 1, which we think of as the empty word and it has degree 0. Note that L is positively graded with graduation given by L :=
{t1, . . . , tm}. The degree (deg) of a word ti1 ti2 . . . tip is p; the degree of f ∈ L is the maximum of the degrees of the words in f. We include among the words a symbol 1, which we think of as the empty word and it has degree 0. Note that L is positively graded with graduation given by L :=  j≥0 Lp, where L0 =
j≥0 Lp, where L0 = 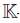 and Lp is spanned by all words of degree p in the alphabet {t1, . . . , tm}, for p > 0. A connected graded algebra B = L/{R} is called a quadratic algebra, if R is a subspace of L2. An algebra is finitely presented, if it is a quotient
and Lp is spanned by all words of degree p in the alphabet {t1, . . . , tm}, for p > 0. A connected graded algebra B = L/{R} is called a quadratic algebra, if R is a subspace of L2. An algebra is finitely presented, if it is a quotient 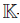 {t1, . . . , tm}/I, where I = {r1, . . . , rs} is a finitely generated two-sided ideal of
{t1, . . . , tm}/I, where I = {r1, . . . , rs} is a finitely generated two-sided ideal of  {t1, . . . , tm}. We call
{t1, . . . , tm}. We call 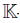 {t1, . . . , tm}/{r1, . . . , rs} a presentation of B with generators t1, . . . , tm and relations r1, . . . , rs. We always assume that r1, . . . , rs is a minimal set of relations for B and every generator ti has degree 1. For B =
{t1, . . . , tm}/{r1, . . . , rs} a presentation of B with generators t1, . . . , tm and relations r1, . . . , rs. We always assume that r1, . . . , rs is a minimal set of relations for B and every generator ti has degree 1. For B =  {t1, . . . , tm}/{r1, . . . , rs} a finitely presented algebra, if the relations r1, . . . , rs are all homogeneous, then B is a connected graded algebra.
{t1, . . . , tm}/{r1, . . . , rs} a finitely presented algebra, if the relations r1, . . . , rs are all homogeneous, then B is a connected graded algebra.
Definition 2.1. A quadratic algebra B is called Koszul, if the trivial left B-module B admits a projective resolution
admits a projective resolution
such that Pn is generated in degree n, for all n ≥ 0.
For more details about Koszul algebras, we refer the reader to Polischuk [26]. Backelin and Fröberg [4] showed several equivalent definitions of Koszul algebras.
Now, we recall the definition of Artin-Schelter regular algebra introduced by Artin and Schelter [3].
Definition 2.2. A connected graded algebra B is said to be Artin-Schelter regular of dimension d, if B has finite global dimension d, finite Gelfand-Kirillov dimension, and ExtiB(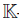 , B) = 0, if i 6 ‡ d, and ExtdB(
, B) = 0, if i 6 ‡ d, and ExtdB(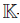 , B)
, B) 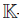 (l), for some integer l.
(l), for some integer l.
Let M be a B-bimodule, and let ν, τ be algebra automorphisms of B. Then τ M ν denotes the induced B-bimodule such that τ M ν = M as a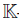 -space, and where a
-space, and where a  m
m  b = τ (a) mν (b), for all a, b ∈ B and all m ∈ τ M ν= M. If τ or ν is the identity map of B, then we write M ν orτ M, respectively. The enveloping algebra of an algebra B is the tensor product Be = B ⊗ Bop, where Bop is the opposite algebra of B. Bimodules over B are essentially the same as modules over the enveloping algebra of B. An algebra B is said to be homologically smooth, if as an Be -module, B has a projective resolution with finite length and such that every term in the projective resolution is finitely generated.
b = τ (a) mν (b), for all a, b ∈ B and all m ∈ τ M ν= M. If τ or ν is the identity map of B, then we write M ν orτ M, respectively. The enveloping algebra of an algebra B is the tensor product Be = B ⊗ Bop, where Bop is the opposite algebra of B. Bimodules over B are essentially the same as modules over the enveloping algebra of B. An algebra B is said to be homologically smooth, if as an Be -module, B has a projective resolution with finite length and such that every term in the projective resolution is finitely generated.
Definition 2.3. A graded algebra B is called skew Calabi-Yau of dimension d, if
as Be -modules, for some integer l.
The automorphism ν is called the Nakayama automorphism of B. If, in addition, Be is isomorphic to B as Be -modules, or equivalently, ν is inner, then B is called Calabi-Yau of dimension d.
Next, we recall the definition of our objects of interest introduced by Gallego and Lezama [8].
Definition 2.4. Let R and A be rings. We say that A is a skew P BW extension over R, if the following conditions hold:
(i) R (the subring of coefficients) is a subring of A sharing the same identity element.
(ii) There exist finitely many elements x1, . . . , xn ∈ A such that A is a left free Rmodule, with basis the set of standard monomials Mon(A) := {x α: = x 1α1 · · · x nα n | α = (α1, . . . , αn) ∈
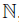 n}. Moreover, x 01 · · · x 0n: = 1 ∈ Mon(A).
n}. Moreover, x 01 · · · x 0n: = 1 ∈ Mon(A).(iii) For every 1 ≤ i ≤ n and any r ∈ R \ {0}, there exists an element ci,r ∈ R \ {0} such that xir − ci,rxi ∈ R.
(iv) For 1 ≤ i, j ≤ n, there exists di,j ∈ R \ {0} such that
If A is a skew PBW extension over R, then we denote it by A := σ(R){x1, . . . , xn}. For X = x α = x 1α1 · · · x nαn ∈ Mon(A), deg(X) = α1 + · · · + αn.
The notation and the name of the skew PBW extensions are due to the following proposition.
Proposition 2.5 ([8], Proposition 3). Let A = σ(R){x1, . . . , xn} be a skew P BW extension of R. For each 1 ≤ i ≤ n, there exists an injective endomorphism σi: R → R and a σi-derivation δi: R → R such that xir = σi(r)xi + δi(r), where r ∈ R.
From now on, σi and δi are the injective endomorphisms and σi-derivations, respectively, as in Proposition 2.5. A skew PBW extension A is called bijective, if σi is bijective and di,j is invertible, for any 1 ≤ i < j ≤ n. A is called quasi-commutative, if the conditions (iii) and (iv) in Definition 2.4 are replaced by the following:
(iii’) for each 1 ≤ i ≤ n and every r ∈ R \ {0}, there exists ci,r ∈ R \ {0} such that xir = ci,rxi ;
(iv’) for any 1 ≤ i, j ≤ n, there exists di,j ∈ R \ {0} such that xjxi = di,jxixj .
Different examples of skew PBW extensions can be found in Lezama et al., [20] and Suárez [35]. Ring and theoretic properties of these objects have been studied by the authors in [28, 30, 31].
The next result is key to define graded skew P BW extensions (see Definition 2.4).
Proposition 2.6 ([35], Proposition 2.7(ii)). Let A = σ(R){x1, . . . , xn} be a bijective skew P BW extension over an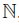 -graded algebra R =
-graded algebra R =  m≥0 Rm. If the following conditions hold,
m≥0 Rm. If the following conditions hold,
(i) σiis a graded ring homomorphism and δi : R(−1) → R is a graded σi-derivation, for all 1 ≤ i ≤ n, and
(ii) xjxi − di,jxixj ∈ R2 + R1x1 + · · · + R1xn, as in (1) and di,j ∈ R0,
then A is an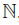 -graded algebra with graduation given by A =
-graded algebra with graduation given by A =  p≥0 Ap, where, for p ≥ 0, Ap is the
p≥0 Ap, where, for p ≥ 0, Ap is the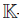 -spacegenerated by the set
-spacegenerated by the set
Definition 2.7 ([35], Definition 2.6). Let A = σ(R){x1, . . . , xn} be a bijective skew P BW extension over an 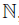 -graded algebra R =
-graded algebra R =  m≥0 Rm. If A satisfies the conditions (i) and (ii) established in Proposition 2.6, then we say that A is a graded skew PBW extension over R.
m≥0 Rm. If A satisfies the conditions (i) and (ii) established in Proposition 2.6, then we say that A is a graded skew PBW extension over R.
Remark 2.8. If A = σ(R){x1, . . . , xn} is a quasi-commutative skew PBW extension over a ring R, then A is isomorphic to an iterated Ore extension of endomorphism type ([20], Theorem 2.3). Nevertheless, skew PBW extensions of endomorphism type are more general than iterated Ore extensions. With the aim of illustrating the differences between these structures, we consider the situations with two and three indeterminates.
If we take the iterated Ore extension of endomorphism type R[x; σx][y; σy], by definition (see Ore [25] or Goodearl and Warfield [10]), for any element r ∈ R, we have the following relations: xr = σx(r)x, yr = σy(r)y, and yx = σy(x)y. On the other hand, if we have σ(R){x, y} a skew P BW extension of endomorphism type over R, then for any r ∈ R, by Definition 2.4, we have the relations xr = σ1(r)x, yr = σ2(r)y, and yx = d1,2xy + r0 + r1x + r2y, for some elements d1,2, r0, r1 and r2 belong to R. When we compare the defining relations of both algebraic structures, it is clear which one of them is more general.
Now, if we have the iterated Ore extension R[x; σx][y; σy][z; σz], then for any r ∈ R, xr = σx(r)x, yr = σy(r)y, zr = σz(r)z, yx = σy(x)y, zx = σz(x)z, zy = σz(y)z. On the other hand, for the skew PBW extension of automorphism type σ(R){x, y, z}, we have the relations given by xr = σ1(r)x, yr = σ2(r)y, zr = σ3(r)z, yx = d1,2xy + r0 + r1x + r2y + r3z, zx = d1,3xz + r ´0 + r ´ 1x + r ´ 2 y + r ´ 3z, and zy = d2,3yz + r´´0 + r´´1x + r´´2y + r ´´3 z, for some elements d1,2, d1,3, d2,3, r0, r0 0 , r´´0 , r1, r´1 , r´´1 , r2, r´2 , r´´2 , r3, r´3 , r´´3 of R. Of course, as the number of indeterminates increases, the differences between both algebraic structures are more remarkable.
As we can expect from these facts, graded iterated Ore extensions are strictly contained in graded skew PBW extensions, see Suárez [35], Remark 2.11. Examples of graded skew PBW extensions can be found in Suárez et al., [9, 35, 36].
The following proposition contains several results about skew P BW extensions and it will be useful in the next section.
Proposition 2.9. Let A = σ(R){x1, . . . , xn} be a graded skew P BW extension.
(i) If R is graded Noetherian, then A is graded Noetherian ([36], Proposition 2.7).
(ii) If A is quasi-commutative, then R is Koszul if and only if A is Koszul ([35], Proposition 3.3).
(iii) If R is Koszul finitely presented, then A is Koszul ([35], Theorem 5.5).
(iv) If R is Artin-Schelter regular and A is quasi-commutative, then A is Artin-Schelter regular ([36], Theorem 3.6).
(v) If R is a finitely presented connected Auslander-regular algebra, then A is ArtinSchelter regular ([36], Proposition 3.5).
(vi) If A is quasi-commutative, R is connected and skew Calabi-Yau of dimension d, then A is skew Calabi-Yau of dimension d + n ([36], Theorem 4.5 (i)).
(vii) If R is finitely presented connected Auslander-regular, then A is skew Calabi-Yau ([36], Theorem 4.5 (ii)).
Zhang and Zhang in [43] introduced a special class of algebras called double Ore extensions.
Definition 2.10 ([43], Definition 1.3). Let R be an algebra and A be another algebra containing R as a subring.
(i) A is generated by R and two new variables x1 and x2.
(ii) The variables {x1, x2} satisfy the relation
where p12, p11 ∈ 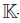 and τ1, τ2, τ0 ∈ R.
and τ1, τ2, τ0 ∈ R.
(ib) A is generated by R and two new variables x1 and x2.
(iib) The variables {x1, x2} satisfy the relation
where p´12, p´11 ∈ 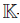 and τ´1, τ ´2 , τ ´0 ∈ R.
and τ´1, τ ´2 , τ ´0 ∈ R.
(iii) A is a double Ore extension, if it is left and right double Ore extension of R with the same generating set {x1,x2}.
(iv) A is a graded right (left) double Ore extension, if all relations of A are homogeneous with assignment deg(x1) = deg(x2) = 1.
Let P denote the set of scalar parameters {p12, p11} and let τ denote the set {τ1, τ2, τ0}. We call P the parameter and τ the tail (see [43], p. 2671). By considering the datum P, Zhu et al., [45] defined a matrix 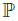 ∈ M2(
∈ M2( ) in the following way:
) in the following way:
By using the ideas given in [43], p. 2671, we rewrite the condition (3) above as follows:
Writing
it is clear that σ is a  -linear map from R to M2(R), δ is a
-linear map from R to M2(R), δ is a 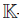 -linear map from R to the column R-module R⊕2: =
-linear map from R to the column R-module R⊕2: = , and σ and δ are uniquely determined. In this way, equation (5) can also be written as
, and σ and δ are uniquely determined. In this way, equation (5) can also be written as
which is a generalization of the multiplication in an Ore extension.
Let A be a right double Ore extension of R. Having in mind Definition 2.10, all symbols of {P, σ, δ, τ} are now defined. When no confusion arises, a right double Ore extension or a double Ore extension A is also denoted by A = RP [x1, x2; σ, δ, τ ]. Let A = RP [x1, x2; σ, δ, τ ] be a right double Ore extension. If δ is a zero map and τ consists of zero elements, then the right double Ore extension is denoted by RP [x1, x2; σ] and is called a trimmed right double Ore extension (see [43, Convention 1.6]).
Lemma 2.11 ([43], Lemma 1.7). If A = RP [x1, x2; σ, δ, τ ] is a right double Ore extension of R with {σ, δ} defined as in (5), then the following holds:
(i) σ : R → M2(R) is an algebra homomorphism.
(ii) δ : R → R⊕2 is a σ-derivation.
(iii) If σ : R → M2(R) is an algebra homomorphism and δ: R → R⊕2 is a σ-derivation, then (5) holds for all elements r ∈ R if and only if it holds for a set of generators.
By Lemma 2.11, when A = RP [x1, x2; σ, δ, τ ] is a right double Ore extension, then σ is an algebra homomorphism and δ a σ-derivation. We now call σ a homomorphism, δ a derivation. Note that homomorphism σ is not surjective, so it cannot be invertible in the usual sense. Zhang and Zhang [43] defined invertibility of σ in right double Ore extensions.
Definition 2.12 ([43], Definition 1.8). Let σ : R → M2(R) be an algebra homomorphism. We say that σ is invertible, if there exists an algebra homomorphism
satisfying the following conditions:
for all r ∈ R. Equivalently,
where • is the multiplication of the matrix algebra M2(EndK(R)). The multiplication of EndK(A) is the composition of 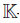 -linear maps. The map φ is called the inverse of σ.
-linear maps. The map φ is called the inverse of σ.
Let A = RP [x1, x2; σ, δ, τ ] be a right double Ore extension. Zhang and Zhang [43] introduced the 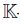 -linear map detP σ : R → R of σ :=
-linear map detP σ : R → R of σ := , which is called the P-determinant.
, which is called the P-determinant.
Definition 2.13. If A = RP [x1, x2; σ, δ, τ ] is a right double Ore extension, then the P-determinant of σ is defined to be
Remark 2.14. If P = {1, 0}, then det P σ = σ22σ11 − σ12σ21. If p12 ‡ 0, then det P σ = −p−112 p11σ11σ22 − p −112 σ21σ12 + σ11σ22 (see [43], p. 2677). Moreover, det P σ is an algebra endomorphism of R (see Zhang [43], Proposition 2.1).
Let V be a finite-dimensional vector space and T(V ) be the tensor algebra with the usual grading. A connected graded algebra B = T(V )/hRi is quadratic, if R is a subspace of V ⊗2. The homogeneous dual of B is then defined as B! = T(V ∗ )/{R⊥}, where V ∗ is the dual space of V and R⊥ = {λ ∈ V ∗ ⊗ V ∗ | λ(r) = 0, for all r ∈ R}. If B = T(V )/{R} is a Koszul algebra, then its Yoneda algebra is defined as E(B) :=  i∈N ExtiB (
i∈N ExtiB ( ,
, ) which is isomorphic to B! . For a graded automorphism ν of B, we define a map ν ∗: V ∗ → V ∗ by ν ∗ (f)(x) = f(ν(x)), for each f ∈ V ∗ and x ∈ V . Note that ν induces a graded automorphism of B! because ν is assumed to preserve the relation space R. We still use the notation ν ∗ for this algebra automorphism (see Zhun [45], p. 559).
) which is isomorphic to B! . For a graded automorphism ν of B, we define a map ν ∗: V ∗ → V ∗ by ν ∗ (f)(x) = f(ν(x)), for each f ∈ V ∗ and x ∈ V . Note that ν induces a graded automorphism of B! because ν is assumed to preserve the relation space R. We still use the notation ν ∗ for this algebra automorphism (see Zhun [45], p. 559).
Proposition 2.15 ([41], Proposition 1.11). Let B be a Koszul Artin-Schelter regular algebra with global dimension d. If ν is a graded automorphism of B and ν ∗ is its corresponding dual graded automorphism of the dual algebra B! , then there exists a unique c in the multiplicative group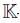 \ {0} such that ν ∗ (u) = cu, for all u ∈ ExtdA (
\ {0} such that ν ∗ (u) = cu, for all u ∈ ExtdA (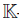 ,
, ).
).
In [16] the homological determinant of a graded automorphism of an Artin-Schelter Gorenstein algebra was defined to study the noncommutative invariant theory. Since every Artin-Schelter Gorenstein algebra is Artin-Schelter regular, then for an Artin-Schelter Gorenstein algebra B, its homological determinant, denoted hdet, it is a homomorphism from the graded automorphism group of B to the multiplicative group  \ {0}. The precise definition and its application can be found in [16, 27]. We use Proposition 2.15 to define the homological determinant.
\ {0}. The precise definition and its application can be found in [16, 27]. We use Proposition 2.15 to define the homological determinant.
Definition 2.16 ([41], Definition 1.5). Let B be a Koszul Artin-Schelter regular algebra and let ν be a graded automorphism of B. The homological determinant hdet(ν) of σ is defined as hdet(ν) := c, where c is as in Proposition 2.15.
Zhu et al., [45] defined the homological determinant of σ, denoted hdetM, in the following way:
Definition 2.17 ([45], Definition 2.5). Let B be a Koszul Artin-Schelter regular algebra. Let σ : B → M2(B) be an algebra homomorphism and let σ ∗ : B! → M2(B! ) be the dual homomorphism of algebras. The homological determinant of σ, denoted by hdetM(σ), is defined to be
for W, X, Y, Z ∈  satisfying σ∗ (x0) =
satisfying σ∗ (x0) =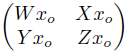 , where x0 is a base element of the highest nonzero component B!d , which is 1-dimensional
, where x0 is a base element of the highest nonzero component B!d , which is 1-dimensional  -space, of B! .
-space, of B! .
Some properties, applications and examples of the homological determinant of σ can be found in Zhun et al., [45].
3. Main results
In this section, we present the new results for graded skew P BW extensions concerning ring-theoretic properties.
Theorem 3.1. If A = σ(R){x1, . . . , xn} is a graded skew P BW extension over a finitely presented Koszul Auslander-regular algebra R, then the homological determinant of the Nakayama automorphism of A is 1.
Proof. Since R is finitely presented Koszul, Proposition 2.9(iii) asserts that A is Koszul. Moreover, since R is Koszul, it is known that R is quadratic, and therefore connected. By assumption that R is Auslander-regular, and by Proposition 2.9(v), we have that A is Artin-Schelter regular. Note that by Proposition 2.9(vii), A is skew Calabi-Yau and there is the Nakayama automorphism ν of A. Now, since R is Auslander-regular, necessarily it is Noetherian. Thus, by Proposition 2.9(i), A is Noetherian. Finally, by Reyes et al., [27], Theorem 6.3, hdet(ν) = 1.
Corollary 3.2. If A = σ(R){x1, . . . , xn} is a graded skew P BW extension over the commutative polynomial ring R =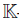 [t1, . . . , tm], then the homological determinant of the Nakayama automorphism of A is 1.
[t1, . . . , tm], then the homological determinant of the Nakayama automorphism of A is 1.
Example 3.3. Some algebras which are graded skew P BW extensions over commutative polynomial rings are the following:
Let g be a finite dimensional Lie algebra over k with basis x1, . . . , xn and U(g) its enveloping algebra. The homogenized enveloping algebra of g is A(g) := T(g ⊕ kz)/ hRi, where T(g ⊕ kz) is the tensor algebra, z is a new indeterminate, and R is spanned by the union of sets {z ⊗ x − x ⊗ z | x ∈ g} and {x ⊗ y − y ⊗ x − [x, y] ⊗ z | x, y ∈ g}. The algebra A(g) is a skew P BW extension over k[z] (c.f. Suárez et al., [37], Section 2.2).
The Jordan Algebra introduced by Jordan [15] is the free k-algebra J defined by J := k{x, y}/{yx − xy − y2 }. It is immediate that this algebra is not a skew polynomial ring of automorphism type but an easy computation shows that J
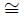 σ(k[y]){x}.
σ(k[y]){x}.Diffusion algebras arose in physics as a possible way to understand a large class of 1-dimensional stochastic process, see [14]. A diffusion algebra A with non-zero parameters aij in the complex numbers
 , is an algebra over
, is an algebra over generated by variables x1, . . . , xn subject to relations aijxixj −bijxjxi = rjxi −rixj , whenever i < j, bij , ri ∈
generated by variables x1, . . . , xn subject to relations aijxixj −bijxjxi = rjxi −rixj , whenever i < j, bij , ri ∈ , for all i < j, such that the indeterminates x’s form a
, for all i < j, such that the indeterminates x’s form a -basis of the algebra A. In the applications to physics the parameters aij are strictly positive reals and the parameters bij are positive reals as they are unnormalised measures of probability. One can see that these algebras are not skew polynomial rings over
-basis of the algebra A. In the applications to physics the parameters aij are strictly positive reals and the parameters bij are positive reals as they are unnormalised measures of probability. One can see that these algebras are not skew polynomial rings over [x1, . . . , xn] but are skew P BW extensions over this ring (see [32], Section 5.3).
[x1, . . . , xn] but are skew P BW extensions over this ring (see [32], Section 5.3).
Theorem 3.4. Let A = σ(R){x1, x2} be a graded skew P BW extension over a connected algebra R.
(i) A is a connected graded double Ore extension RP [x1, x2; σ, δ, τ ], where
with σ1, σ2, δ1and δ2 as in Proposition 2.5 and d1,2as in (1).
(ii) detP σ = σ2σ1, P = {c1,2, 0} and
(iii) σ is invertible with inverse
such that for all r ∈ R, the equation
holds for
(iv)
Proof. Suppose that A = σ(R){x1, x2} is a graded skew PBW extension of a connected algebra R. It is clear that A is a connected algebra. (i) Definition 2.4 (iii) establishes that for all r ∈ R \ {0}, there are elements c1,r, c2,r, c1,0, c2,0 ∈ R, with c1,r, c2,r ‡ 0, such that
In this way, for all r ∈ R, σ1(r) = c1,r, σ2(r) = c2,r, δ1(r) = c1,0, δ2(r) = c2,0, where σ1, σ2, δ1 and δ2 are as in Proposition 2.5. From [9], Theorem 3.2, we can assert that A is a connected graded double Ore extension RP [x1, x2; σ, δ, τ ]. (ii) Comparing relations (5) and (8), we have that
Therefore,
Hence, det P σ = σ2σ1. Now, from Definition 2.4 (iv), we know that there exists an element c1,2 ∈ R \ {0} such that
with r0, r1, r2 ∈ R. By assumption, A is graded, so deg(r0) = 2, deg(r1) = deg(r2) = 1 and deg(c1,2) = 0. Since R is connected, R0 =  , whence c1,2 ∈
, whence c1,2 ∈  \ {0}. Comparing (2) and (9), we have that p12 = c1,2, p11 = 0, τ1 = r1, τ2 = r2, τ0 = r0. Thus P = {c1,2, 0} and
\ {0}. Comparing (2) and (9), we have that p12 = c1,2, p11 = 0, τ1 = r1, τ2 = r2, τ0 = r0. Thus P = {c1,2, 0} and
(iii) By (i) and Zhun et al., [45], Lemma 1.8(1), we have that σ is invertible with its inverse given by
such that the equation r(x1x2) = (x1x2)φ(r) + δ ´ (r) holds for some
Then rx1 = x1φ11(r) + x2φ21(r) + δ´1 (r) and rx2 = x1φ12(r) + x2φ22(r) + δ´2 (r). Now, since A = σ(R){x1, x2} is a skew PBW extension, then
and
By Definition 2.4(ii), in Equation 10 we have that
and
Since A is a graded skew PBW extension, then A is bijective and therefore σ1 and σ2 are bijective. So, by Equation (12), σ −1 1 = φ11 and by Equation (13) we have that φ21 = 0 and −δ1(φ11) = −δ1(σ 1−1 ) = δ´1 . Analogous to the above reasoning we have φ12 = 0 and −δ2(σ 2−1 ) = δ´2 . (iv) It follows from (i) and [43], Proposition 1.14(a).
Theorem 3.5. Let R be a Koszul Artin-Schelter regular algebra with Nakayama automorphism ν and let A = σ(R){x1, x2} be a graded quasi-commutative Calabi-Yau skew P BW extension. Then
where σ1, σ2 are as in Proposition 2.5 and d1,2 is as in (1).
Proof. Since A is a connected graded quasi-commutative skew PBW extension of R then by [9], Corollary 3.3, we have that A is a connected graded trimmed right double Ore extension of R, of the form A = RP [x1, x2; σ]. By Theorem 3.4, det P σ = σ2σ1 and
By the assumption, R is Artin-Schelter regular and A is quasi-commutative, so Proposition 2.9(iv) implies that A is Artin-Schelter regular. Since R is Koszul then by Proposition
2.9(iii) we have that A is Koszul. Since A is Calabi-Yau, then by Zhun [45], Theorem 3.12,
i.e.,
According to the calculations presented in [45], Example 2.7,
which implies that hdet(σ1) = c1,2, and hdet(σ2) = 
Corollary 3.6. If A = σ(R){x1, x2} is a graded quasi-commutative skew P BW extension over a Koszul Artin-Schelter regular algebra R with Nakayama automorphism ν, then
Proof. From the proof of Theorem 3.5, we know that A is a Koszul Artin-Schelter regular connected graded trimmed right double Ore extension of R given by A = RP [x1, x2; σ]. (i) By [45], Proposition 3.11, the Nakayama automorphism µ of A is given by
Now, from Theorem 3.4, we have that
By replacing (16) in (15), we obtain (14).
(ii) If A is Calabi-Yau, then by Theorem 3.5, ν = σ2σ1 and
Conversely, by replacing ν = σ2σ1 and
in (14), we have that µ is the identity map of A. Definition 2.3 asserts that A is CalabiYau.