English (pdf)
Article in xml format
Article references
Automatic translation
Send this article by e-mail
Cited by SciELO 
Cited by Google 
Similars in
SciELO 
Similars in Google 
Permalink
Introduction
Spectral imaging (SI) techniques capture spectral information at each spatial location of a scene to identify the composition and structure of a target [1]; for instance, in remote sensing to analyze land properties, in artwork to preserve paintings, and in biomedical imaging to detect anomalies and diseases [2]-[4].
Traditional SI sensors scan a number of regions that grow linearly in proportion to the desired spatial and spectral resolution [5]. In contrast, compressive spectral imaging (CSI) captures the spatio-spectral information with few 2-dimensional (2D) random and multiplexed projections [6].
The coded aperture snapshot spectral imager (CASSI) is a CSI optical architecture that utilizes binary random coded apertures and a dispersive element to attain compressed measurements of a scene [7], [8]. A binary coded aperture is an optical element with opaque and translucent elements that block/unblock the light passing through. The quality of the CASSI measurements is determined by the coded aperture patterns; well coded apertures provide good measurements [9].
A 3-dimensional (3D) data cube is commonly recovered from coded projections by solving a compressive-sensing-based minimization algorithm, which assumes that the scene is highly compressible when represented in some known orthonormal basis [10]-[12]. The matrix completion (MC) framework introduced in [13], [14] does not require prior knowledge since it relies on a low-rank matrix structure to recover the scene from a small subset of accurately observed entries [15], [16]. For this, MC demands that the number of measurements is enough and uniformly distributed such that, at least one entry in every row and column of the matrix can be observed with high probability [14].
This paper uses MC in the reconstruction process since the high correlation exhibited by natural spectral scenes indicates an underlying low-rank structure [17], [18] and thus avoids the prior knowledge of the representation basis required by the traditional CSI approach. For this, we design optimal coded aperture patterns that provide CASSI measurements benefiting the MC constraints to obtain high-quality reconstructions. The optimal patterns are those that reduce the multiplexing phenomena mixing spectral information of different spatial locations occurring in CASSI. This multiplexing can be reduced by maximizing the distance between the translucent elements in the coded aperture pattern, maintaining a high compression ratio, and guaranteeing a uniform distribution, such that the known values in the incomplete matrix will be uniformly distributed.
To evaluate the efficiency of the designed coded aperture patterns, they were compared to traditional ones, such as randomly generated and complementary Boolean coded apertures, which ensure that each spatial location of the scene is detected once and only once [8]. Simulations using two different spectral datasets show average improvements of 3 to 9 dB in reconstruction PSNR over the random coded apertures and 1 to 3 dB over the complementary coded apertures.
1. Materials and methods
1.1. The coded aperture snapshot spectral imager sensing process
The compressed measurements in CASSI are obtained optically by a coded aperture, a dispersive element, and an FPA detector. Figure 1 shows a schematic representation of the main components in CASSI. Given the spectral image source density f 0 (x, y, λ), coding is obtained by using a coded aperture T(x, y) that blocks/unblocks energy in the (x, y) spatial coordinates across the λ wavelengths. The resulting coded field f 1 (x, y, λ) is dispersed by the prism S(λ) to separate the light into its spectrum components. The compressive measurements are finally attained by the integration of the dispersed field over the detector spectral range sensitivity.
The discretized output at the detector for a single snapshot of a discrete spectral data cube F ∈ RN x N x L with N X N pixels of spatial resolution and L spectral bands can be modeled as
(1)
for k = 0,1, ..., N □ 1, j = 0,1, ..., N + L □ 1, where Y kj is the intensity measured at the (k, j)th position of the detector whose dimensions are N X (N + L □ 1); T k(j-i) represents the binary coded aperture, and □kj accounts for noise.
The CASSI architecture has recently been modified to capture multiple snapshots, each applying a different coded aperture pattern T(x, y). Capturing multiple snapshots from a scene provides additional information that yields improved signal reconstruction [12]. The process of capturing K snapshots can be represented in the standard form of an undetermined system of linear equations as follows
(2)
Where 
is the CASSI sensing matrix including the coded and dispersed effect of the K snapshots, θ is the sparse representation of the scene on a representation basis 
represents system noise.
1.2. Matrix completion technique
MC is a methodology to recover a low-rank or approximately low-rank matrix from a given subset of its entries. As shown in [13], there exists only one low- rank matrix fitting the observed entries with high probability if the number of measurements are sufficient and uniformly sensed. The MC recovery process can be modeled as an optimization problem
(3)
Where S ∈ RmXn is the decision variable representing the estimated matrix, rank (S) is the rank of the matrix S, M contains the observed entries of the unknown matrix with
is the set containing the indices of the observed entries, and 
is a projection operator defined as
(4)
The optimization problem in Eq. (3) is NP-hard, and all known algorithms require time doubly exponential in the dimension d = max (m, n) of the matrix S [19]. To solve this problem, two main approaches are presented in the literature. The first, based on nuclear norm minimization, was introduced in [13] as the tightest convex relaxation of Eq. (3). However, it requires certain incoherence conditions and the cardinality |Ω| to be of the order O(dr log d). The cost of these algorithms depends on the computational time of singular value decomposition, which increases in proportion to the size and rank of the underlying matrices. The second approach is based on the minimization of the Grassmann Manifold and proposes a reformulation of the problem to make it more suitable for solving large-scale problems as follows,
(5)
Where ||•||F denotes the Frobenius norm, that is, the square root of the absolute squares of the elements of a matrix 
. Algorithms
in [20]-[22] solve the problem in Eq. (5). In particular, the low-rank matrix fitting algorithm (LMaFit) introduced in [23] solves a non-convex formulation of the problem in Eq. (5), which factorizes the unknown matrix into the product of two matrices S = UV and minimizes the distance between the factorization and an auxiliary matrix Z with a projection in Ω that must be equal to that of the known entries M. This approach iteratively finds an approximation of S by alternating the optimization over variables U and V. The LMaFit problem is modeled as
(6)
Where 
. The LMaFit software, used in this paper to reconstruct the spectral scenes under the MC approach, is distributed under the terms of the GNU General Public License and is available online [24].
1.3. Spectral image recovery using MC and CASSI measurements
Unlike the 2D matrices commonly recovered by MC, the spectral scenes in this paper contain 3D information; then, the recovery process for HSI scenes using MC exploit the independence property of the CASSI system along the data cube rows. Figure 2 illustrates a discretized model of the CASSI sensing phenomena. Note that the pattern tq affecting the qth row slice of the data cube Sq is independent from the patterns affecting the other slices. Additionally, as each coded row transverses the prism, it is shifted only along the x □ axis and the coded projection on the detector, row y, results mutually independent from the others.
Considering this property, the data cube F can be decomposed into N matrices, each matrix corresponding to one row slice. To generalize the independence of the row slices, let the kth slice Sk∈RNxL of F be defined as (Sji)k = Fk,j,i for k = 0, ..., q, ..., N-1. The data cube is represented as F = {S0; ...; Sq ; ...; SN-1}. Similarly, the coded aperture T∈RNxL affecting the entire data cube can be expressed 
. Finally, the CASSI measurements of the FPA Y are expressed as 
, where yk ∈ RN+L_1 are the CASSI measurements of the row slice Sk coded by the aperture tk ∈ RN. The spectral scene is recovered with MC by independently reconstructing each slice Sk from its corresponding measurements yk. The estimated data cube F e RNxNxL is obtained by concatenating the solutions of the N optimization problems
(7)
for k = 0, 1, …, N - 1 where Sk = Uk Vk represents the estimation for the matrix slice Sk and the data cube is estimated as 
1.4. Optimal coded aperture design
The proposed coded aperture design satisfies the MC conditions when the scene is sensed with the CASSI system. The first MC condition dictates that the observed entries must be uniformly distributed such that, each row and column have at least one observation, otherwise, one could never guess the information in the row or column. The second condition is that the number of accurately observed entries must be sufficiently large, given that, if Ω has cardinality |Ω| = p >≥ Cd5/4r logd, then the recovery is exact with a probability of at least 1 - cd-3, where C and c are two constants [13].
To satisfy the first MC condition, multiple snapshots with complementary coded aperture patterns are required to gather sufficient information for the reconstruction process such that each column of each matrix slice Sk is observed once and only once. To satisfy the second condition, we define a desirable CASSI measurement as one where the multiplexing phenomena, that mixes spectral information in each single spatial location on the detector, is reduced as much as possible, thus reducing inaccurate entries. This desirable projection is attained if the patterns are designed such that they avoid multiplexing when the scene is dispersed by the prism.
Figure 3 compares a desirable and an unwanted CASSI measurement for MC. Observe in Figure 3a that the desirable projection is attained when the distance between the translucent elements in the pattern corresponds to at least the number of spectral bands.
Source: Authors' own elaboration.
Figure 3 Comparison of a desirable and an unwanted CASSI measurement to increase estimation quality by MC methodology
In contrast, in Figure 3b the pattern does not avoid multiplexing, and an unwanted projection with no accurate entries is attained. The designed coded aperture then maximizes the separation between each pair of translucent elements over the same row as much as possible. This maximum distance is bounded above by the number of spectral bands in the data cube (L) since more separation results in poor light throughout the system. With these arrangements, let 
be the designed coded aperture pattern set, where 
represents the pattern for K snapshots affecting the matrix slice Sr Each optimal pattern tk is attained by solving the integer optimization problem in Eq. (8).
(8)
for L = 0, 1, …, K-1 and j, j' = 0, 1, …, N-1, where D is a decision variable representing the minimum distance between two translucent elements for each row in the coded aperture pattern. Finally, (tl) is a binary decision variable representing the block/unblock pattern for the L th snapshot in the j th spatial location. The designed coded aperture patterns are randomly used for each single matrix slice in the acquisition process.
The data cube is recovered from the coded projections by solving independently the MC problem for each row slice in the detector using the LMaFit algorithm, which requires a matrix Mk∈RNxL, where PΩ(Mk) are the entries to recover the row slice Sk in the locations in Q. However, the CASSI system only provides an array yk∈MN+L-1 on the detector. The input matrix Mk is obtained from the captured array by a back-projection of the K snapshots in the k th row as follows
(9)
For j, k = 0, …, N - 1, I =0, …, L - 1 and L = 0,1, …, K - 1 snapshots, where F represents the number of wavelengths multiplexed in each coded projection, 
, with α = max (0, j + i + 1 - L) and b = min (j + i, N - 1). Ideally, the value of E for the MC technique should be 1, representing accurate information. However, it is necessary to consider the multiplexed information to guarantee the information is sufficient for reconstruction.
2. Results
To test the designed coded apertures, the quality of the estimations of two data cubes using designed patterns was compared to the quality of traditional random and complementary coded aperture patterns. The peak signal to noise ratio (PSNR) was used as the comparison quality metric. The PSNR is defined as the ratio of the maximum possible power of a signal and the power of corrupting noise that affects the fidelity of its representation. The PSNR for the estimated data cube is the average of the PSNR., i = 0, 1, ..., L - 1 per spectral band of the data cube, which is defined as
(10)
Where Fi represents the i th spectral band, F i is the estimation of the matrix Fi, max (Fi)2 is the maximum possible pixel value of the image Fi, and MSE is the mean squared error of the image Fi and its approximation F i given by
(11)
The experiments use 2 different test data cubes: F1 with 256 X 256 pixels of spatial resolution and L = 16 spectral bands taken from [25], and F2 with 512 X 512 pixels of spatial resolution and L = 24 spectral bands taken from the multispectral databases of Columbia University [26]. All simulations assume the rank of the spectral scenes to be equal to one.
Figure 4 depicts zoomed versions of the first two patterns of the coded aperture set with K = 5 snapshots and with transmittance equal to 1/K for 3 different distributions.
Source: Authors' own elaboration.
Figure 4 Comparison of the three coded aperture pattern sets used to modulate the source light and to capture the compressed measurements
Note that, the random patterns in Figure 4a do not guarantee that each spatial location is sensed because there are locations where the voxel is blocked in both snapshots; therefore, the first MC condition is not satisfied. The complementary coded apertures in Figure 4b guarantee that information in each voxel is sensed only once; however, they do not correctly modulate the field to avoid the multiplexing of the information when the dispersive effect occurs. Finally, in Figure 4c the designed coded aperture patterns are shown to be complementary and maximize the distance between the translucent elements, which will minimize the multiplexing phenomena in the sensing CASSI process.
Figures 5 a and 5 b show a comparison of the average spatial PSNR attained for 10 simulations for the data cubes F1 and F2 using the 3 different coded aperture patterns. The highest PSNR value is obtained when the designed pattern set is used; an improvement of up to 3 dBs compared to estimations with the complementary (Boolean) coded aperture set and up to 9 dBs compared to reconstructions with the random coded aperture set. Note that there is not an increment in the PSNR for the random coded aperture as the number of snapshots is increased. This occurs because the random patterns hardly satisfy the requirement of having at least one observation for each row and column of the unknown matrix despite taking many more snapshots. Figures 5c and 5d show the percentage of accurate observed entries 0 attained for a different number of captured snapshots. 0 is calculated as the ratio of the number of translucent element pairs in the same row whose separation is at least the number of spectral bands v, and the total number of acquired measurements KN (N + L - 1). Accurate entries are obtained by O = v/KN (N + L-1). The greater the number of accurate entries, the higher the value of the PSNR attained, as dictated by MC.
The matrix slice reconstructions were obtained for 70% of the total entries, no matter if they were accurate or mixed, to guarantee sufficient entries to reconstruct the scene using the LMaFit algorithm; the 30% of the information was estimated.
To evaluate the fidelity and quality of the spectral information, Figure 6 shows a comparison of the spectral signature (SS) of three randomly selected spatial locations of the scenes obtained using 3 different distributions for data cubes F1 and F2 when K = 12 snapshots. A high-quality estimate of the spectral signatures is obtained when the designed patterns are used.
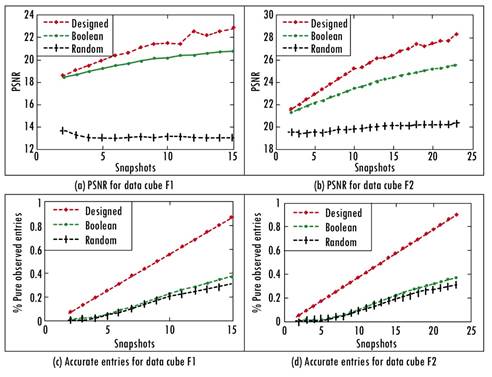
Source: Authors' own elaboration.
Figure 5 PSNR and the percentage of accurately observed entries obtained using the three different coded aperture pattern sets for data cubes F1 and
3. Discussion
This paper introduced optimal coded aperture patterns to solve the compressive spectral imaging inverse problem using the MC framework. The proposed designs were tested and show good reconstructions for this methodology, which can be useful when there is no prior information about the basis of representation where the scene is sparse. This approach can also be valuable when the low-rank property is more evident than the sparsity. The MC methodology requires strong constraints on the accuracy of entries, which can be contrary to the multiplexing process of the CS approach.
A desirable CASSI measurement for the MC reconstruction approach is defined as one that reduces the multiplexing of the spectral information. This concern can be confusing since one of the main concepts in CASSI is multiplexing so that information from many voxels can be captured at once. The proposed approach reduces the multiplexing phenomena as much as possible, but it is constrained to maintain the compression ratio, and the transmittance is defined by the number of snapshots. Because of reduced multiplexing, more snapshots are required to provide sufficient information for reconstruction, especially for those cases where the scene is not smooth. Under no circumstances will the number of snapshots exceed the number of spectral bands in the scene. Therefore, the proportion of light throughout the system using the designed patterns is equivalent to that using the traditional random and complementary patterns.
It was found by simulations that using 70% of the observed entries, without considering if they were accurate or multiplexed, provided sufficient measurements for each row and column of the matrix row slices to have at least one observation, which obtains a good MC reconstruction. When fewer observations were used, the MC constraint was not satisfied, and we obtained poor reconstructions, such as those estimations obtained with random coded aperture patterns since this distribution does not guarantee gathering information from all the voxels despite capturing more snapshots. When more measurements were used, the degrees of freedom of the LMaFit algorithm were reduced; missing values could not be estimated because the matrix was almost complete, and the reconstructions were not different from the input entries. Not satisfying the MC constraints can result in poor reconstructions containing hole-like artifacts such as those in Figure 7.
Source: Authors' own elaboration.
Figure 7 Visual comparison of data cubes F1 and F2 using three different coded aperture sets for K = 12 snapshots
As future work, the proposed coded aperture patterns can be tested with traditional algorithms and the optimal coded aperture patterns that can be found in the literature, such as those proposed in [9], [12], to compare the performance of the designed patterns without considering the reconstruction algorithm.
Conclusions
The design of a coded aperture set for compressive spectral matrix completion is proposed. The coded apertures are attained by solving an integer optimization problem that maximizes the distance between each translucent element in the coded aperture pattern. The designed set maximizes the number of accurately observed entries captured by means of the CASSI system and back-projection guarantees that each column and each row have at least one observed entry, thus satisfying the MC conditions. The results show higher quality reconstructions when the designed coded aperture set is used compared to the traditional random and complementary coded apertures. The improvement attained is 1 to 3 dBs over the complementary coded aperture set and 3 to 9 dBs over the random coded aperture set. A visual comparison of the signal signature recovered using the three coded aperture patterns in three different spatial locations was obtained to evaluate and confirm the improvement of quality across the spectral dimension.
