Artículo de investigación/Research article

Desempeño de las técnicas de agrupamiento para resolver el problema de ruteo con múltiples depósitos

Performance of clustering techniques for solving multi depot vehicle routing problem

Eliana M. Toro-Ocampo¹,Andrés H. Domínguez-Castaño², Antonio H. Escobar-Zuluaga³

¹MSc. en Investigación de Operaciones y Estadística, Facultad de Ingeniería Industrial, Universidad Tecnológica de Pereira, Pereira-Colombia, elianam@utp.edu.co

²MSc. en Ingeniería Eléctrica, Universidad Tecnológica de Pereira, Pereira-Colombia, ahdominguez@utp.edu.co

³PhD. en Ingeniería Eléctrica, Escuela de Tecnología Eléctrica, Universidad Tecnológica de Pereira, Universidad Tecnológica de Pereira, Pereira-Colombia, aescobar@utp.edu.co

Fecha de recepción:  17 de junio de 2015/ Fecha de aceptación:17 de noviembre de 2016

Como citar / How to cite

Eliana M. Toro-Ocampo, Andrés H. Domínguez-Castaño y Antonio H. Escobar-Zuluaga, “Desempeño de las técnicas de clusterización para resolver el problema de ruteo con múltiples depósitos”, Tecno Lógicas, vol. 19, no. 36, pp. 49-62, 2016.

Resumen

El problema de ruteo de vehículos considerando múltiples depósitos es clasificado como NP duro, cuya solución busca determinar simultáneamente las rutas de un conjunto de vehículos, atendiendo un conjunto de clientes con una demanda determinada. La función objetivo del problema consiste en minimizar el total de la distancia recorrida por  las rutas, teniendo en cuenta que todos los clientes deben ser atendidos cumpliendo restricciones de capacidad de depósitos y vehículos. En este artículo se propone una metodología híbrida que combina las técnicas aglomerativas de clusterización para generar soluciones iniciales con un algoritmo de búsqueda local iterada, iterated location search (ILS) para resolver el problema. Aunque en trabajos previos se proponen los métodos de clusterización como estrategias para generar soluciones de inicio, en este trabajo se potencia la búsqueda sobre el sistema de información obtenido después de aplicar el método de clusterización. Además se realiza un extenso análisis sobre el desempeño de las técnicas de clusterización y su impacto en el valor de la función objetivo. El desempeño de la metodología propuesta es factible y efectivo para resolver el problema en cuanto a la calidad de las respuestas y los tiempos computacionales obtenidos, sobre las instancias de la literatura evaluadas.

Palabras clave: Búsqueda local iterada, optimización combinatoria, ruteo con múltiples depósitos, red de distribución, técnicas de agrupamiento.

Abstract

The vehicle routing problem considering multiple depots is classified as NP-hard. MDVRP determines simultaneously the routes of a set of vehicles and aims to meet a set of clients with a known demand. The objective function of the problem is to minimize the total distance traveled by the routes given that all customers must be served considering capacity constraints in depots and vehicles. This paper presents a hybrid methodology that combines agglomerative clustering techniques to generate initial solutions with an iterated local search algorithm (ILS) to solve the problem.  Although previous studies clustering methods have been proposed like strategies to generate initial solutions, in this work the search is intensified on the information generated after applying the clustering technique. Besides an extensive analysis on the performance of techniques, and their effect in the final solution is performed. The operation of the proposed methodology is feasible and effective to solve the problem regarding the quality of the answers and computational times obtained on request evaluated literature.

Keywords: Combinatorial optimization, clustering techniques, distribution network, iterated local search, Multi-Depot Vehicle Routing.

1. Introducción

En el gerenciamiento óptimo de la cadena de suministros debe gestionarse de forma eficiente la distribución de materias primas y mercancías a través de la red de distribución. Esta eficiencia se mide a menudo en las entregas oportunas a los usuarios finales. El problema de ruteo considerando múltiples depósitos, Multi-Depot Vehicle Routing Problem (MDVRP) es formulado como una red logística, que pretende resolver, entre otros aspectos, la atención a los clientes en el menor tiempo posible. El MDVRP es una variante del problema de ruteo de vehículos, Vehicle Routing Problem (VRP), el cual corresponde al nombre genérico de una temática que involucra una gran variedad de problemas de optimización combinatorial [1], [2]. Estos problemas son de gran interés en el área académica y de negocios debido a sus múltiples aplicaciones a nivel empresarial, militar y gubernamental en el campo logístico.

Las principales contribuciones de este artículo son: 1) Comparación de diferentes técnicas y estrategias de clusterización para generar soluciones de inicio y su efecto en el desempeño del ILS aplicada en la solución del MDVRP. 2) La estructura de información, tipo árbol, obtenida de la técnica de clusterización que es utilizada para construir soluciones iniciales. Cada nivel el árbol es explorado de forma iterativa a fin de encontrar la mejor solución posible. 3) El uso de heurísticas como inicializadores, para identificar regiones promisorias que faciliten el desempeño de un algoritmo de optimización, de forma que se puedan encontrar soluciones diversas de buena calidad en tiempos computacionales cortos.

2.Estado del Arte

El MDVRP se puede identificar en una gran variedad de contextos y su correcta solución permite una reducción considerable en los costos de distribución. Estudios de casos documentados incluyen entrega de alimentos procesados [3], distribución de productos químicos [4], reparto de bebidas gaseosas,[5] distribución de productos en empresas multinacionales [6], distribución de gases industriales [7], despacho de vehículos cisterna con derivados de petróleo [8], distribución de alimentos lácteos [9].

Para la solución MDVRP se han aplicado técnicas heurísticas y técnicas exactas.

En cuanto a las técnicas exactas, Baldacci y Mingozzi [10] proponen un método basado en el procedimiento de generación sistemática de límites con base en la propuesta de Christofides et al. [11]. El algoritmo exacto utiliza tres tipos de procedimientos para generar límites inferiores, basados en relajación lineal y en relajación lagrangeana, realizadas a la formulación matemática. Los procedimientos propuestos reducen el número de variables del modelo matemático, lo que permite resolver el problema resultante de forma exacta utilizando un software comercial de de programación lineal entera. Baldacci et al. [12] describen una formulación de programación entera del problema de ruteo vehículos con visita periódicas, Periodic Vehicle Routing Problem (PVRP), que se utiliza para obtener diferentes límites inferiores. El MDVRP se puede formular como un PVRP debido a que los depósitos pueden modelarse como los múltiples periodos en el contexto de un PVRP. Por lo tanto, cualquier algoritmo que resuelve el PVRP también puede resolver el MDVRP. Contardo y Martinelli [13] presentan un algoritmo exacto, el cual utiliza dos formulaciones para el MDVRP, usadas en diferentes etapas del algoritmo. Se agregan varios conjuntos de restricciones válidas para fortalecer los modelos propuestos.

Los algoritmos heurísticos han sido adoptados para resolver los problemas de MDVRPs debido a que son metodologías que encuentran soluciones de forma rápida, además de ser relativamente fácil de implementar. Salhi et al. [14] proponen una heurística multinivel con dos pruebas de reducción. Las soluciones iniciales factibles se construyen en el primer nivel, mientras que en los otros niveles son mejoradas mediante heurísticas inter e intra depósito [15].

Giosa et al. [16] implementó la estrategia de “agrupar primero y rutear después”, aplicada a una variante del MDVRP que considera ventanas de tiempo, MDVRP with Time Windows (MDVRPTW). En la etapa de clusterización se asignan los clientes a los depósitos, luego cada clúster se resuelve usando el algoritmo de ahorros. El artículo realiza un estudio computacional con seis diferentes técnicas de clusterización. Nagy et al. [17] resuelven una variante del MDVRP donde se consideran entregas y recogidas simultáneas, Multi-depot VRP with mixed Pickup and Delivery (MDVRPMPD). La metodología es desarrollada en varias etapas: i)  Divide el conjunto de clientes en limítrofes y no limítrofes.  ii) Asigna los clientes no limítrofes al depósito más cercano iii) Para cada depósito se encuentra una solución factible que se obtiene de la solución del problema de ruteo con entregas y recogidas considerando un depósito, Vehicle Routing Problem with Pickups and Deliveries (VRPPD). iv) Se insertan los clientes limítrofes en las rutas encontradas en el paso anterior.  Luego se realizan procedimientos de mejoramiento a través de heurísticas como 2 y 3-OPT, reinserciones e intercambios.

Lee et al. [18] plantean el MDVRP como un problema de programación dinámica determinística, con estados finitos, luego usan el algoritmo heurístico de la ruta más corta para resolverlo. Crevier et al. [19] proponen una heurística que combina el método de búsqueda tabú con la programación lineal entera, en esta aproximación los vehículos pueden ser reabastecidos en depósitos intermedios a lo largo de la ruta. Jeon et al. [20] proponen un algoritmo genético híbrido para el MDVRP, el cual considera el mejoramiento de una solución inicial mediante tres heurísticas y una tasa de mutación flotante para escapar de óptimos locales. Ho et al. [21] desarrollaron dos algoritmos genéticos híbridos (HGA1 y HGA2). La mayor diferencia entre los genéticos es la forma en que se generan las soluciones iniciales; en el HGA1 se generan de forma aleatoria. El algoritmo de ahorros de Clarke and Wright [22] y el algoritmo del vecino más cercano fueron incorporados en el proceso de inicialización del HGA2. El desempeño de ambos algoritmos es evaluado usando dos instancias generadas de forma aleatoria, donde se consideran 2 depósitos, 50 y 100 clientes.

Sureka y Sumathi [23] resuelven el problema a través de un algoritmo genético. Los clientes son agrupados con base en la distancia a los depósitos más cercanos y luego son ruteados con el algoritmo de ahorros de Clarke and Wright [22]. Luego se realiza el procedimiento de optimización usando el algoritmo genético. Cordeau y Maischberger [24] presentan una heurística paralela con conceptos de búsqueda tabú. La metodología resuelve diferentes variantes del VRP, entre ellas el MDVRP. La heurística lcombina el Búsqueda Tabú con un simple mecanismo de perturbación para garantizar la exploración del espacio de búsqueda y además se describe la implementación paralela de la heurística. Vidal et al. [25] proponen un algoritmo genético híbrido donde se permiten tanto soluciones factibles como infactibles, las cuales son separadas en dos grupos. Se aplica sucesivamente un número de operadores para seleccionar dos individuos padres y combinarlos. El nuevo individuo hijo, generado inicialmente, es mejorado usando procedimientos de búsqueda local y luego es incluido en la subpoblación apropiada con relación a su factibilidad. Este es un método muy eficiente y alcanza todos los óptimos de la literatura.

Subramanian et al. [26] proponen una técnica matheurística que combinan una secuencia de modelos lineales enteros mixtos con columnas que corresponden a rutas, las cuales son generadas mediante una aproximación metaheurística. Esta metodología resuelve diferentes variantes del VRP, entre ellas el MDVRP y el MDVRPMPD. Escobar et al. [27]  proponen un algoritmo búsqueda tabú  granular híbrido, el cual considera diferentes vecindarios y estrategias de diversificación para mejorar la solución inicial obtenida, mediante un procedimiento híbrido. Los resultados obtenidos son competitivos en cuanto a calidad de las respuestas y tiempos computacionales. Finalmente, Montoya- Torres et al. [2] presentan un completo estado del arte del MDVRP donde relaciona 173 publicaciones publicadas desde 1988 hasta 2014. Hacen un recorrido por diferentes variantes del problema como: ventanas de tiempo, división de las entregas, recogidas y entregas simultáneas en la misma ruta y flota heterogénea. Otro aspecto importante es que el documento presenta tanto los abordajes mono-objetivo como multiobjetivo que se han desarrollado para resolver el problema, así como líneas futuras de investigación.

3. Modelo Matemático

El MDVRP puede ser definido como un conjunto de Depósitos I  y clientes J, donde el objetivo es encontrar una secuencia factible de entregas a través de un conjunto de rutas, las cuales deben minimizar la distancia o el tiempo, de forma que se atiendan todos los clientes de la red.  A cada arco (i,j) ϵ I UJ se le asocia un costo de viaje cij. Cada cliente j ∈ J tiene una demanda dj, la cual debe ser atendida en su totalidad en una sola visita. Un conjunto de K vehículos idénticos con capacidad Qk está disponible en cada depósito. El MDVRP es un problema NP-duro debido a que simultáneamente se deben determinar las rutas de una flota de vehículos que inician desde diferentes depósitos. El objetivo es determinar un conjunto de rutas que minimice la distancia del recorrido, para realizar todas las entregas o el tiempo invertido en la atención de todos los clientes. Se deben cumplir de forma estricta las siguientes restricciones: i) La demanda de cada cliente debe ser atendida por un único vehículo. ii) Cada vehículo inicia y termina su ruta en el mismo depósito. iii) La totalidad de la demanda de cada ruta no debe exceder la capacidad del vehículo. El modelo que se presenta a continuación, corresponde al presentado por Surekha y Sumathi [23].

La función objetivo (8) minimiza la distancia total de todas las rutas. La ecuación (9) establece que cada cliente debe ser asignado a una ruta. La ecuación (10) representa la restricción de capacidad del conjunto de vehículos. El conjunto de restricciones de eliminación de sub-tours está representado por (11). Las restricciones de conservación de flujo son expresadas mediante (12). La ecuación (13) garantiza que cada vehículo atiende una única ruta. Las restricciones de capacidad de los depósitos están dadas por (14). La ecuación (15) especifica que un cliente puede ser asignado a un depósito, únicamente si hay una ruta que parte desde el depósito y transita a través del cliente. Las restricciones (16), (17) definen la naturaleza binaria de las variables xijk, zij. Finalmente la restricción (18) define Ulk como una variable no negativa continua.

Formulación del problema

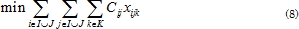
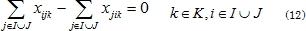
4. Técnicas de Clusterización

Los Métodos jerárquicos y otros algoritmos de agrupamiento representan un intento para encontrar “buenos" clústeres de una nube de datos. Generalmente no es posible examinar todas las posibilidades de agrupamiento, para conjuntos de datos de gran volumen [28]. Varios autores han utilizado técnicas de agrupamiento en diferentes algoritmos para resolver diferentes variantes del VRP entre ellos, Giosa et al. [16] en el MDVRP y Barreto et al. [29] en el CLRP, ambos con resultados promisorios. Los algoritmos de agrupamiento jerárquico implican un proceso secuencial. En cada paso del enfoque jerárquico de agrupamiento, una observación o un conjunto de observaciones se va fusionado en otro grupo. En todos los métodos se inicia el procedimiento con base en la matriz de distancias entre clientes, definida como la distancia inicial entre cada clúster. Se debe tener en cuenta que al inicio del proceso cada cliente forma un clúster. Ci representa el clúster i con ni  clientes  y Cj  representa el clúster j con nj clientes.

Las diferentes métricas de clusterización usadas en este estudio son: Distancia mínima, single linkage (SL); Distancia máxima, Complete Linkage (CL), Distancia promedio no ponderada, unweight aritmethic average (UAL), Promedio ponderado, weighted aritmethic (AL), Método del centroide ponderado, Weighted centroid method (WCM), Método de la mediana, Centroid method unweight (CMU), Método de ward, Ward's method (W). [28] En la Tabla 2 se presentan Las ecuaciones de las métricas.

Adicionalmente a los métodos de clusterización, se implementó una heurística constructiva que se describe a continuación.

Heurística constructiva (HC): esta heurística hace una selección aleatoria de clientes asignándolos al depósito más cercano. La localización de los clientes se realiza con base en la capacidad del depósito. Cuando se alcanza la capacidad del depósito, los clientes restantes serán asignados al depósito más cercano. El procedimiento se repite hasta cuando todos los clientes han sido ubicados a los depósitos.

5. Metodología de Solución

Para resolver el MDVRP se implementó el algoritmo ILS, [30] este es un método de búsqueda local aleatorio que genera una secuencia de soluciones obtenida mediante una heurística integrada. Su estructura se fundamenta en 3 pasos: i) Procedimiento de solución inicial. ii) Procedimiento de búsqueda local. iii) Perturbación.

5.1 Estructura de Datos

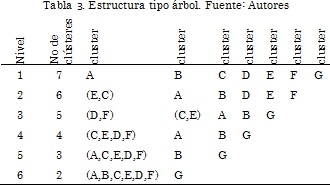
La estructura de datos implementada es una estructura de árbol, donde los terminales corresponden a los clústeres. La distancia entre ellos corresponde a una métrica elegida de la Tabla 2. Supóngase que después de aplicar el método de clusterización se obtiene un arreglo de clústeres como el que se presenta en la Tabla 3. En la Tabla 3 en el nivel 1 se tienen 7 clústeres, debido a que cada individuo es un clúster en el paso inicial. A medida que se va ascendiendo de nivel se van disminuyendo la cantidad de clústeres, hasta llegar a 2 clústeres como se observa en el nivel 6.

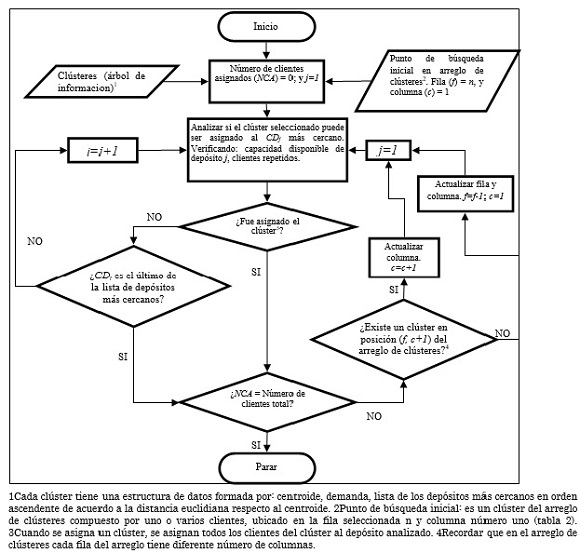
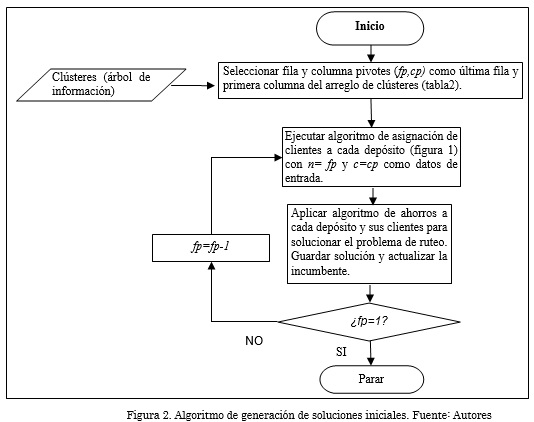
5.2 Procedimiento para Generar la Solución Inicial

La metodología para generar las soluciones iniciales se representa en los diagramas de flujo de la Fig. 1 y Fig. 2. Este procedimiento tiene como insumo la información de clústeres de la Tabla 3. El diagrama de flujo de la Fig. 1 es un procedimiento interno del diagrama de flujo de la Fig. 2 y entre ambos establecen una búsqueda exhaustiva hasta encontrar la configuración de menor costo posible. El resultado de este procedimiento corresponde a la solución inicial del algoritmo ILS.

5.3 Procedimiento de Búsqueda Local

El algoritmo de búsqueda contiene dos tipos de operadores de mejora, Intra-ruta e Inter-ruta, los cuales se enumeran en dos listas. A partir de la solución de inicio generada en el paso anterior, se da inicio a la búsqueda local, cuyo objetivo es mejorar la solución actual usando los operadores o estructuras de vecindad. El procedimiento se ejecuta de la siguiente manera: 1) Seleccionar un operador al azar de la lista de estructuras de vecindad inter-ruta. Si hay alguna mejora ir al paso 3, de lo contrario, ir al paso 2. 2) En caso de que la aplicación de la estructura de vecindad no pueda mejorar la solución incumbente, prohibirla para la próxima selección. Si todas las estructuras de vecindad han sido prohibidas, la búsqueda local se detiene. En caso contrario ir al paso 1. 3) Seleccionar una estructura de vecindad de la lista de operadores intra-ruta. Si hay una mejora, ir al paso 5. De lo contrario, ir al paso 4. 4) Si la aplicación de la estructura de vecindad dentro de la ruta no puede mejorar la solución actual, la estructura queda prohibida para las selecciones posteriores. Ir al paso 1 Si se han prohibido todas las estructuras de vecindad intra-ruta. De lo contrario ir al paso 3. 5) Ir al paso 3.

La lista de estructuras de vecindad inter-ruta usada es: shift(1,0), shift (2,0), shift(3,0), swap(1,1), swap(1,2), swap(2,2), 2-OPT, La lista intra-ruta está formada por: swap(1,1), shift (1,0),2-OPT [15].

5.4 Algoritmo de perturbación

El procedimiento de perturbación se lleva a cabo con clientes seleccionados aleatoriamente, los cuales deben pertenecer a diferentes rutas. Los operadores usados para tal fin son: swap (1, 1), swap (2, 1), swap (2, 2), shift (1, 0), shift (2, 0). El operador seleccionado se aplica dos veces y de forma consecutiva.  Para aplicar el operador se debe cumplir que la distancia entre los clientes seleccionados, no sobrepasen los límites de una distancia que es calculada a cada paso. Este valor se calcula como el promedio de la distancia del depósito asociado al primer cliente, respecto a los dos depósitos más cercanos. Esa distancia es afectada por un factor β seleccionado aleatoriamente y de acuerdo a pruebas preliminares debe estar entre [0.1 - 1.0].

6. Análisis Resultados

El algoritmo fue implementado en C++ y ejecutado en un computador Intel i5-3470 3,2 GHZ, 8 GB. La metodología es validada y comparada con las instancias propuestas por Cordeau et al.[19]. Se realizaron pruebas preliminares intensivas para encontrar los parámetros de mejor desempeño. El criterio de parada del algoritmo fue definido en 800.000 iteraciones globales. El factor β de mejor desempeño se obtiene mediante la generación de un valor aleatorio entre 0,1 y 1. En la fase de perturbación se realizan hasta 50 intentos para identificar el cliente 2, debido a que se deben cumplir la condiciones de que pertenezca a una ruta diferente de la del cliente 1 y a que este ubicado dentro del radio permitido.

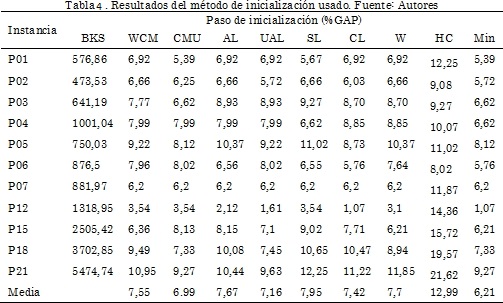
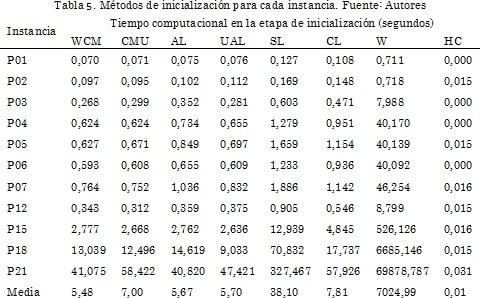
Los resultados de la Tabla 4 corresponden a las mejores soluciones encontradas después de realizar 10 corridas por métrica de clusterización. Como se observa, las soluciones iniciales encontradas tienen valores similares en cuanto a la función objetivo, a excepción de las obtenidas con la HC. En la Tabla 5 se presentan los tiempos computacionales, la técnica HC es la de menor consumo, por el contario W es la de mayor consumo.

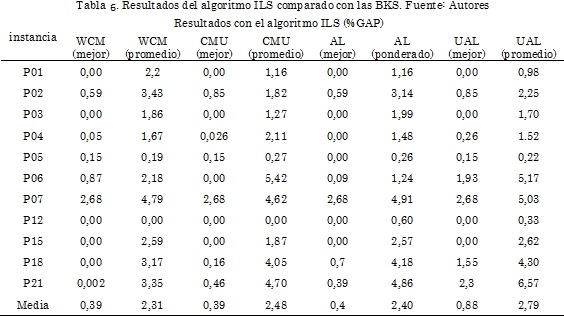
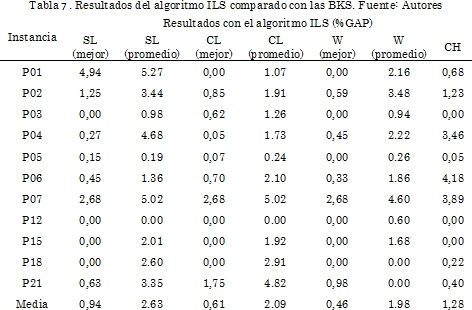
En la Tabla 6 y Tabla 7 se presenta el desempeño del algoritmo propuesto, se realizaron 10 corridas por método de clusterización, se reporta el promedio y la mejor solución obtenida. El tiempo de cálculo más bajo se obtiene cuando se utiliza CMU como estrategia de inicialización. En la mayoría de casos que utilizan esa técnica de clusterización como estrategia de inicio se puede ver que las soluciones son de buena calidad. La solución promedio de menor calidad en la etapa de optimización es la solución inicial utilizando HC, sin embargo, es la que utiliza menos tiempo de cálculo en la etapa inicial.

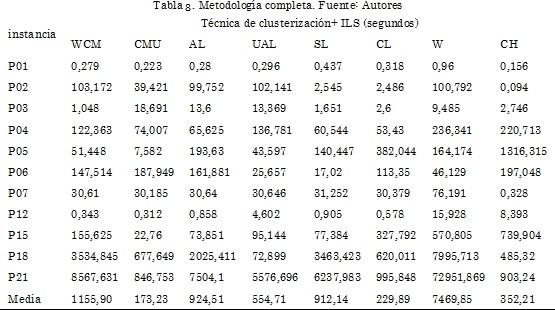
En la Tabla 8 se presenta el tiempo total requerido para el funcionamiento de la metodología completa que incluye la técnica de la clusterización y una versión básica del algoritmo de ILS. El hecho de la obtención de soluciones de diferente calidad en la fase de optimización utilizando el algoritmo ILS muestra que las heurísticas utilizadas como inicializadores, identifican soluciones en diferentes puntos del espacio de soluciones. Este aspecto es conveniente para hacer una búsqueda diversa, en el espacio de soluciones.

Comparando los BKS contra las soluciones iniciales encontradas con técnicas de clusterización, se observa que estas técnicas localizan los clientes al depósito más cercano, en un porcentaje superior al 80 % en todos los casos, lo que demuestra la fortaleza de las mismas. El algoritmo de optimización presenta un buen rendimiento, ya que pasa de 6.21 % en la etapa inicial hasta 0.30 % de GAP en la etapa de optimización. Para los 11 casos analizados se obtuvo el BKS en 6 de ellos. Para P21, la instancia más grande, se obtuvo una configuración óptima totalmente diferente a la reportada en la literatura. Se puede decir, en general, que las técnicas de clusterización usadas como inicializadores facilitan el desarrollo de la técnica ILS para encontrar soluciones de alta calidad en tiempos computacionales razonables.

7. Conclusiones

Se propuso un mecanismo eficiente de exploración a la estructura tipo árbol, generada después de aplicar las técnicas de clusterización. Este entrega soluciones iniciales de buena calidad en tiempos computacionales muy cortos. Se proponen diferentes técnicas heurísticas que se utilizan como inicializadores para el MDVRP. Su análisis se realiza teniendo en cuenta el tiempo y la calidad de las soluciones tanto iniciales como finales. No se puede llegar a la conclusión de que específicamente una técnica de agrupamiento es la adecuada para la solución de todos los casos. Sin embargo, en promedio, la heurística con mejor desempeño es CMU en los casos de mayor tamaño.

Encontrar diferentes soluciones de inicio de buena calidad mediante la aplicación de diferentes técnicas de clusterización se constituyen en una ventaja cuando se implementan algoritmos poblacionales, en las que el éxito se basa en la diversidad de la población inicial, la cual debe mantenerse durante todo el proceso con el fin de asegurar una búsqueda adecuada del espacio de soluciones. Se propone como trabajo futuro implementar una metaheurística poblacional empleando diferentes estrategias de clusterización para generar las soluciones de inicio.

8. Agradecimientos

Los autores agradecen a la Universidad Tecnológica de Pereira por el apoyo al proyecto “Optimización multiobjetivo para resolver el problema de ruteo de vehículos asociados a múltiples depósitos considerando técnicas de clusterización", cod. 7-15-1.

Referencias

[1] K. F. Doerner and V. Schmid, “Survey: Matheuristics for rich vehicle routing problems,” in 7th International Workshop on Hybrid Metaheuristics, HM 2010, vol. 6373 LNCS, M. Blesa, C. Blum, G. Raidl, A. Roli, and M. Samples, Eds. Berlin: Springer, 2010, pp. 206-221.         [ Links ]

[2] J. R. Montoya-Torres, J. López Franco, S. Nieto Isaza, H. Felizzola Jiménez, and N. Herazo-Padilla, “A literature review on the vehicle routing problem with multiple depots,” Comput. Ind. Eng., vol. 79, pp. 115-129, Jan. 2015.         [ Links ]

[3] P. Cassidy and H. Bennett, “Vehicle System Scheduling,” OR Soc., vol. 23, no. 2, pp. 151-163, 2015.         [ Links ]

[4] M. Ball, B. Golden, and A. Assad, “Planning for Truck Fleet Size in the Presence of a Common-Carrier Option,” Decis. Sci., vol. 14, no. 1, pp. 103-120, 2007.         [ Links ]

[5] B. L. Golden and E. a. Wasil, “OR Practice--Computerized Vehicle Routing in the Soft Drink Industry,” Oper. Res., vol. 35, no. 1, pp. 6-17, 1987.         [ Links ]

[6] M. Fisher, R. Greenfield, R. Jaikumar, and J. Lester, “A computerized Vehicle Routing Application,” Interfaces (Providence)., vol. 4, pp. 42-52, 1982.         [ Links ]

[7] W. J. Bell, L. M. Dalberto, M. L. Fisher,  a. J. Greenfield, R. Jaikumar, P. Kedia, R. G. Mack, and P. J. Prutzman, “Improving the Distribution of Industrial Gases with an On-Line Computerized Routing and Scheduling Optimizer,” Interfaces (Providence)., vol. 13, no. 6, pp. 4-23, 1983.         [ Links ]

[8] A. G. G. Brown, C. J. Ellis, G. W. Graves, and D. Ronen, “of the dispatching are to minimize cost of delivered product, to balance the workload among the company trucks, and to load the maximum weight on a truck while adhering to all laws. The important,” vol. 17, no. 1, pp. 2-4, 1987.         [ Links ]

[9] J. Pooley, “Integrated Production and Distribution Facility Planning at Ault Foods,” Interfaces (Providence)., vol. 24, no. 4, pp. 113-121, 1994.         [ Links ]

[10] R. Baldacci and A. Mingozzi, “A unified exact method for solving different classes of vehicle routing problems,” Math. Program., vol. 120, no. 2, pp. 347-380, Sep. 2009.         [ Links ]

[11] N. Christofides, A. Mingozzi, and P. Toth, “Exact algorithms for the vehicle routing problem, based on spanning tree and shortest path relaxations,” Math. Program., vol. 20, no. 1, pp. 255-282, Dec. 1981.         [ Links ]

[12] R. Baldacci, E. Bartolini,  a. Mingozzi, and  a. Valletta, “An Exact Algorithm for the Period Routing Problem,” Oper. Res., vol. 59, no. 1, pp. 228-241, 2011.         [ Links ]

[13] C. Contardo and R. Martinelli, “A new exact algorithm for the multi-depot vehicle routing problem under capacity and route length constraints,” Discret. Optim., vol. 12, pp. 129-146, May 2014.         [ Links ]

[14] S. Salhi and M. Sari, “A multi-level composite heuristic for the multi-depot vehicle fleet mix problem,” Eur. J. Oper. Res., vol. 103, no. 1, pp. 95-112, Nov. 1997.         [ Links ]

[15] E. M. Toro O., A. H. Escobar Z., and M. Granada E., “Literature Review On The Vehicle Routing Problem In The Green Transportation Context,” Luna Azul, vol. 42, no. 42, pp. 362-387, Dec. 2015.         [ Links ]

[16] I. D. Giosa, I. L. Tansini, and I. O. Viera, “New assignment algorithms for the multi-depot vehicle routing problem,” J. Oper. Res. Soc., vol. 53, no. 9, pp. 977-984, Sep. 2002.         [ Links ]

[17] G. Nagy and S. Salhi, “Heuristic algorithms for single and multiple depot vehicle routing problems with pickups and deliveries,” Eur. J. Oper. Res., vol. 162, no. 1, pp. 126-141, Apr. 2005.         [ Links ]

[18] C.-G. Lee, M. a. Epelman, C. C. White, and Y. a. Bozer, “A shortest path approach to the multiple-vehicle routing problem with split pick-ups,” Transp. Res. Part B Methodol., vol. 40, no. 4, pp. 265-284, May 2006.         [ Links ]

[19] B. Crevier, J.-F. Cordeau, and G. Laporte, “The multi-depot vehicle routing problem with inter-depot routes,” Eur. J. Oper. Res., vol. 176, no. 2, pp. 756-773, Jan. 2007.         [ Links ]

[20] G. Jeon, H. R. Leep, and J. Y. Shim, “A vehicle routing problem solved by using a hybrid genetic algorithm,” Comput. Ind. Eng., vol. 53, no. 4, pp. 680-692, Nov. 2007.         [ Links ]

[21] W. Ho, G. T. S. Ho, P. Ji, and H. C. W. Lau, “A hybrid genetic algorithm for the multi-depot vehicle routing problem,” Eng. Appl. Artif. Intell., vol. 21, no. 4, pp. 548-557, Jun. 2008.         [ Links ]

[22] G. Clarke and J. W. Wright, “Scheduling of Vehicles from a Central Depot to a Number of Delivery Points,” Oper. Res., vol. 12, no. 4, pp. 568-581, Aug. 1964.         [ Links ]

[23] P. Surekha and S. Sumathi, "Solution To Multi-Depot Vehicle Routing Problem Using Genetic Algorithms,” World Appl. Program., vol. 1, no. 3, pp. 118-131, 2011.         [ Links ]

[24] J.-F. Cordeau and M. Maischberger, “A parallel iterated tabu search heuristic for vehicle routing problems,” Comput. Oper. Res., vol. 39, no. 9, pp. 2033-2050, Sep. 2012.         [ Links ]

[25] T. Vidal and T. G. G. Crainic, “A hybrid genetic algorithm for multidepot and periodic vehicle routing problems,” Oper., vol. 60, no. 3, pp. 611-624, 2012.         [ Links ]

[26] A. Subramanian, E. Uchoa, and L. S. Ochi, “A hybrid algorithm for a class of vehicle routing problems,” Comput. Oper. Res., vol. 40, no. 10, pp. 2519-2531, Oct. 2013.         [ Links ]

[27] J. W. Escobar, R. Linfati, P. Toth, and M. G. Baldoquin, “A hybrid Granular Tabu Search algorithm for the Multi-Depot Vehicle Routing Problem,” J. Heuristics, vol. 20, no. 5, pp. 483-509, Oct. 2014.         [ Links ]

[28] A. C. Rencher, A Review Of “Methods of Multivariate Analysis,” vol. 37, no. 11. 2005.         [ Links ]

[29] S. Barreto, C. Ferreira, J. Paixão, and B. S. Santos, “Using clustering analysis in a capacitated location-routing problem,” Eur. J. Oper. Res., vol. 179, no. 3, pp. 968-977, Jun. 2007.         [ Links ]

[30] A. Subramanian, “Heuristic, Exact and Hybrid Approaches for Vehicle Routing Problems.” Universidade Federal Fluminense, Niteroi, Sao Pablo, pp. 60-69, 2012.         [ Links ]