Allowable blood loss: an exponential model

Mario Javier García
MD. Anestesiólogo. Universidad Industrial de Santander. Email: mjgarciam@hotmail.com.

Recibido: septiembre 4/2009 - Aceptado: noviembre 11/2009

Summary

This article proposes a simple, mathematically-derived formula which could be used for calculating allowable blood loss. Authors have used lineal approaches in many models found in the medical literature; this introduces an important inaccuracy into such prediction. An exponential approach is deduced and explained in the model proposed here which is considered to be much closer to reality than that obtained with the lineal model. More emphasis is placed on the fact that while a patient is losing blood, he/she is simultaneously receiving fluids to keep total blood volume almost constant.

Key words: surgical blood losses, mathematical model, anesthesia (source: MeSH, NLM).

RESUMEN

Se propone una fórmula sencilla, derivada matemáticamente, con el objeto de calcular las pérdidas sanguíneas permisibles. En muchos modelos encontrados en la literatura médica dichas aproximaciones son lineales, lo cual induce un error importante en la predicción. En este modelo se propone, se deduce y se explica una aproximación exponencial considerada mucho más cercana a la realidad. Se valora el proceso de hemodilución observado cuando un paciente pierde sangre, mientras se le infunden líquidos intravenosos, manteniendo la volemia aproximadamente constante.

Palabras clave: pérdidas de sangre quirúrgica, modelos matemáticos, anestesia (fuente: DeCs, Bireme).

INTRODUCTION

Many mathematical models have been proposed for predicting allowable blood loss in patients in whom it has been supposed that they will suffer this type of loss (for example, intraoperative) whilst simultaneously receiving endovenous liquids (crystalloids or colloids)(1-4), keeping total blood volume almost constant.

This situation frequently occurs during surgery (even though it may be observed in hospital services, emergencies and intensive care units) and necessarily becomes the responsibility of the anaesthesiologist in charge.

Many models referenced in the literature propose lineal approaches. If a percentage of a volume of a defined and fixed concentration becomes lost and is replaced by water (for example) then the concentration of the solution in question will become reduced by this exact proportion.

For example, if one has a 100 cc receptacle containing 0.9% SSN and 30 cc are extracted from such solution (the concentration remaining obviously being 0.9%), when replacing the volume removed with 30 cc distilled water then a new solution’s concentration will become exactly reduced by 30% (i.e. by the same percentage of volume withdraw regarding total volume). This pattern is effectively lineal and could be approached by a function of:

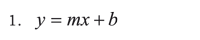
For the example cited above:

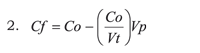
In this case Cf represents final concentration, Co initial concentration, Vp volume lost (withdrawn) and Vt final volume. Analogously to equation 1, Cf will be equivalent to y; Co will be b; Co/Vt will be m, and vp will represent independent variable x.

This is a lineal model. Its Cf vs Vp plot is a straight line, having a negative slope, thereby indicating that final concentration becomes reduced as lost volume increases.

Returning to the clinical area, the intraoperative blood loss model cannot be lineal because this would imply that all the blood lost would be lost from the same haematocrite (from the same concentration) and having the same haemoglobin, which is not true. In every case where an intraoperative patient loses blood whilst receiving endovenous liquids, then such blood is being lost from a different haematocrite; the haematocrite of the lost blood is less in each instance.

Any analysis which ignores this fact is committing a serious error and offers a prediction which is very far removed from reality. Some formulae found in the literature adjust the constants to improve the model; however, with due respect, it could be said that such adjustments seek to "adapt" the model.

The approach proposed here is not just adjusted to reality but also presents a logical and completely rational foundation for explaining the phenomenon, making a contribution from a clinical standpoint and also from scientific, pedagogic and academic points of view.

DEDUCTION

This starts from a consideration which might seem to be contradictory but which is really not so. The approach is lineal for a very small instance (called time differential in mathematics) or for a very small volume (differential volume) (5-6). Such approach will be taken as a starting point to arrive at the following exponential equation:

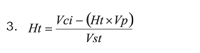
Ht corresponds to haematocrite, Vci initial cellular volume, Vp lost volume and Vst total blood volume. It can be seen that lost volume (Vp) is zero; the equation simply defines the haematocrite (initial cellular volume over total blood volume).

From this equation, one is interested in knowing how haematocrite (Ht) varies according to lost volume (Vp). Ht regarding Vp is thus derived.

Reorganising

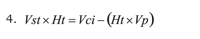
Deriving according to Vp

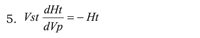
Separating the variables

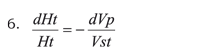
Integrating

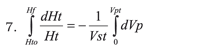
It is worth observing the integration limits. It can be seen that lost volume (Vp) varies between zero and total lost volume whilst haematocrite integration limits vary between initial haematocrite (Hto) and final haematocrite. These limits must be consistent and coherent on each side of the equation. Consequently, lost volume equal to zero "0" should correspond to initial haematocrite and there should be no variations in haematocrite, whilst lost volume is total lost volume (Vpt); haematocrite then corresponds to final haematocrite (Hf).

Integrating

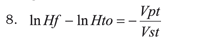
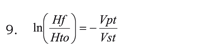
Finally

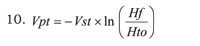
Vpt represents allowable blood loss, given estimated total blood volume (Vst), a known initial haematocrite (Hto) and final haematocrite (Hf), defined in line with an anaesthesiologist’s criteria and according to the clinical considerations which must be born in mind.

As haemoglobin and haematocrite in a particular patient are directly proportional, this equation is equally equivalent if initial haemoglobin and final haemoglobin are used in place of initial haematocrite and final haematocrite:

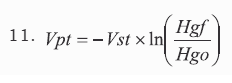
The minus sign accompanying equations 10 and 11 probably attracts one’s attention. This is because the logarithm of a value between 0 and 1 is negative.

Given that natural logarithm function is the inverse function of the exponential function in base e, it is possible that:

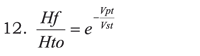
The following is obtained by finding final haematocrite (Hf) value:

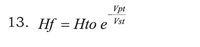
Final haematocrite (Hf) is thus predicted in a patient having certain estimated total blood volume (Vst) with known initial haematocrite (Hto) and certain intraoperative blood volume lost (Vpt). This might become contributory data, combined with gases, clinical data and haemodynamics, leading to deciding whether a transfusion is pertinent (7-9).

Equations 10, 11 and 13 do not involve greater effort and can be easily and rapidly calculated with a conventional calculator having exponential and logarithmic functions.

A function like this can undoubtedly explain, for example, why patients may bleed more from total blood volume. This is not so clear with lineal models, even though it is clinically evident that this condition is (unfortunately) seen with certain frequency.

Example: A patient having 70 Kg body mass and 15.7 g/dl haemoglobin is to undergo pancreatoduodenectomy and one has to calculate allowable blood loss; then, suppose that haemoglobin level is "allowed" to drop to 7, 9 and/or 11 g/dl (i.e. the level of haemoglobin to which a patient "may be allowed" to reach is a decision emanating from the specialist´s criteria and inherent to the clinical conditions of the patient in question.

Such minimum level may be 12 g/dl in a certain case whilst it may only be 7 g/dl in another. The other variable which must be introduced is estimated total blood volume (for this case it will be supposed that it could be 70 ml/kg: 4,900 ml), a value which is also derived from the specialist’s opinion. It would have been very easy to introduce prefixed total blood volume into the formula, depending just on weight; however, this would not be correct, taking existing variability into account according to age, setting and gender. The specialist’s criteria will thus be taken.

Haemoglobin will be allowed to drop to 9 g/dl for the case being proposed.

Thus, applying equation 11:

Now, what would happen if haemoglobin were allowed to drop to 10 g/dl.

The following is given by applying the same equation:

Now, let it be supposed that a patient loses around 1,800 ml of blood during surgery and (for some reason) someone wishes to know (in this case estimate) what final haemoglobin will be. The word calculate is dispensed with, estimate being preferred because the final result is derived from two estimates (total blood volume and blood loss) which, even though apparently measured, are still just estimated.

Using equation 13:

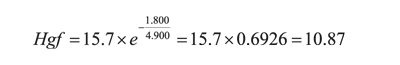
Estimate final haemoglobin will be 10.87 g/dl, following intraoperative loss of around 1,800 cc in a patient having 4,900 cc estimated total blood volume and 15.7 g/dl preoperative measured haemoglobin.

A patient´s low haemoglobin level can be seen when she/he has lost total blood volume; obviously, this will depend on initial haemoglobin. Let us suppose 15 g/dl initial haemoglobin level:

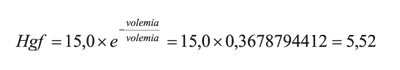
Haemoglobin level will drop to 5.52 g/dl

It can be seen in this case that, assuming that the patient will lose total blood volume, then no specific value need be entered and, consequently, Hgf will only depend on initial haemoglobin.

The same example (loss of total blood volume) could be made with 10 g/dl initial haemoglobin.

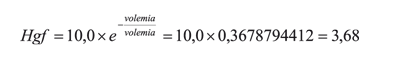
Haemoglobin reaches 3.68 g/dl.

Similarly, it may be supposed that the former patient could lose more than total blood volume (1.5 or 2). The example could be made with a patient having 15 g/dl haemoglobin, supposing that she/he loses 2 total blood volumes:

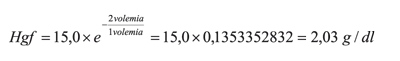
There should be no confusion regarding how blood volume was managed (total and lost) in terms of total blood volume; this could have been done explicitly in any type of unit (e.g. cubic centimetres, litres, etc.) and would have obtained the same result.

In other areas of knowledge, such as neonatology, a neonatologist/paediatrician could be interested in knowing how much blood volume must be changed (if necessary) from a neonate suffering from foetal erythroblastosis contracted by maternal isoimmunisation (10), to be sure of having changed 90% of its blood. Or perhaps ask him/herself, Changing total blood volume once, twice or even three times, which percentage of initial total blood volume has been cleaned of antibodies? These questions may also be answered by the proposal explained here.

EPILOGUE

If one has not become familiar with using a "scientific" calculator and considers that the equations shown here could be useful, then it is suggested that the natural logarithm of the quotient of two haemoglobins in equation 11 be obtained first and then multiplied by the negative of estimated total blood volume. This will facilitate the operation.

On the other hand, base-10 logarithms in most calculators are activated by the Log button whilst natural (base e) logarithms are activated by the Ln button.

It is easier to proceed in the following way when using the exponential equation (equation 13). Obtain the quotient (-Vpt/Vst) and then raise "e" to Ans; this gives the last result obtained in any operation. After having done this then multiply by initial haemoglobin.

It is worth warning that the negative sign is not a triviality which can be adapted with "logic" when managing exponential functions; e²(7.3891) is dramatically different from e-² (0.1353).

REFERENCES

1. Hay SN, Monk TG, Brecher ME. Intraoperative blood salvage: a mathematical perspective. Transfusion. 2002;42(4):451-5.

2. Hahn RG. Estimating allowable blood loss with correction for variations in blood volume. Acta Anaesthesiol Scand. 1989;33(6):508-12.

3. Lorente A. Gasteiger P. Osswald PM. Calculation of the allowable blood loss before transfusion with a programmable pocket calculator.Anaesthesist. 1987;36(6):306-12.

4. Naveen E, Manickam P. Perioperative blood loss assessment. How accurate? Indian J Anaesth. 2006;50(1):35-38.

5. Zill DG. Ecuaciones diferenciales con aplicaciones de modelado. Mexico DF: Thompson; 2002.

6. Óbice WE, DiPrima RC. Ecuaciones diferenciales y problemas con valores en la frontera. Mexico DF: Limusa Wiley; 2006.

7. Park CK. The comparison between the postoperative predicted and actual hematocrite. Korean J Anesthesiol. 1998;35(4):732-7.

8. Weiskopf RB. Efficacy of acute normovolemic hemodilution assessed as a function of fraction of blood volume lost. Anesthesiology. 2001;94(3):439-446.

9. Weiskopf RB. Mathematical analysis of isovolemic hemodilution indicates that it can decrease the need for allogeneic blood transfusion. Transfusión. 1995; 35(8):712-3.

10. Kliegman RM. El feto y el recién nacido. In: Behrman RE, Kliegman RM, editors. Tratado de pediatria. Madrid: McGraw-Hill; 1992.

Conflicto de intereses: ninguno declarado.