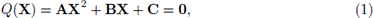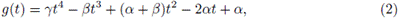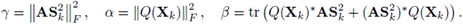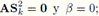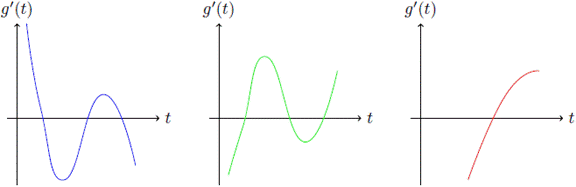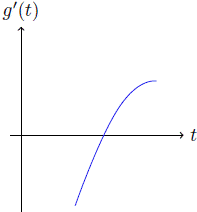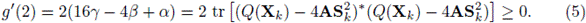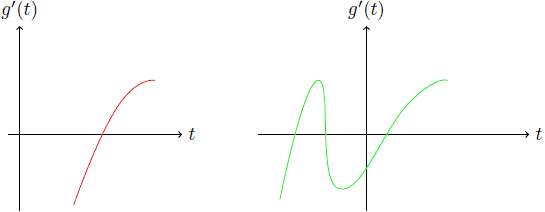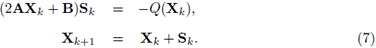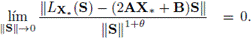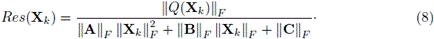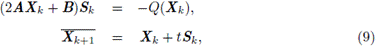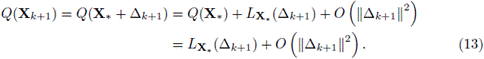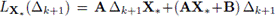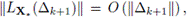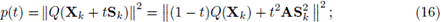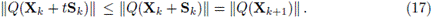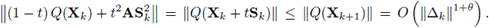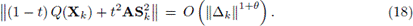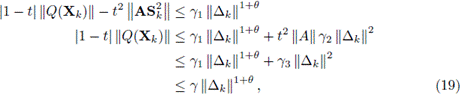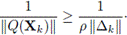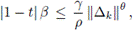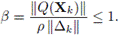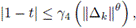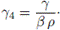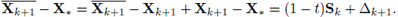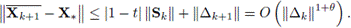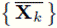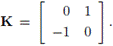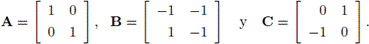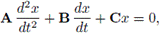Español (pdf)
Articulo en XML
Referencias del artículo
Traducción automática
Enviar articulo por email
Citado por SciELO 
Citado por Google 
Similares en
SciELO 
Similares en Google 
Permalink
1. Introducción
En [16] los autores proponen un algoritmo cuasi-Newton local y hasta cuadráticamente convergente, para resolver la ecuación cuadrática matricial
donde
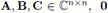es la matriz cero en
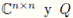es una función cuadrática matricial, el cual reduce el costo computacional del método de Newton-Schur tradicionalmente usado para resolver dicha ecuación ([10], [15]).
Las numerosas aplicaciones en las cuales surge la ecuación matricial (1) han motivado un gran interés en su estudio y el desarrollo de algoritmos para su solución. Áreas en las cuales surge la ecuación cuadrática matricial son el análisis dinámico de mecánica estructural y sistemas acústicos ([1], [22]), simulación de circuitos eléctricos [14], mecánica de fluidos [21], procesamiento de señales [[4], [11]), problemas de vibración y modelamiento de sistemas mecánicos microelectrónicos ([3], [2], [13]).
El algoritmo propuesto en [16], por ser un algoritmo local, es ventajoso siempre que la matriz inicial esté suficientemente cerca de la solución, pero pierde su efectividad en caso contrario. Una alternativa a esta situación es introducir en este algoritmo una estrategia de globalización, como por ejemplo una búsqueda lineal ([6], [20]).
En la literatura sobre algoritmos tipo Newton globalizados para resolver la ecuación (1), se destaca en primer lugar, por su amplio uso, el algoritmo de Newton-Schur globalizado propuesto en [10], donde se introduce una estrategia de globalización análoga a la búsqueda lineal exacta usada en algoritmos de optimización de funciones vectoriales [6]. En segundo lugar, se menciona el algoritmo propuesto en [15], que modifica el algoritmo propuesto en [10] controlando la cercanía entre el paso de Newton y el solvente o solución de la ecuación matricial. Para ello, se compara el tamaño del valor de la función en el paso de Newton (en alguna norma) con cero, ya que en este caso no es necesario hacer una búsqueda lineal, y como consecuencia el algoritmo resultante es menos costoso computacionalmente.
Teniendo en cuenta las ventajas de un algoritmo global y las bondades del algoritmo cuasi-Newton local propuesto en [16], en el presente artículo se propone una globalización de este algoritmo cuasi-Newton para resolver la ecuación cuadrática matricial (1). Para ello, se incorpora al algoritmo cuasi-Newton local una estrategia de búsqueda lineal exacta análoga a la usada en [10] y una modificación de la alternativa usada en [15] para evitar la búsqueda lineal cerca de la solución. Adicionalmente, se demuestra que la estrategia de búsqueda lineal exacta no afecta la convergencia hasta de orden cuadrático obtenida en [16]. También se analiza el desempeño numérico del algoritmo propuesto con el algoritmo de Newton-Schur frecuentemente usado para resolver la ecuación cuadrática. Además, para apreciar la venta ja de tener un algoritmo global frente a uno local, se compara su desempeño con el algoritmo propuesto en [16].
Organizamos este artículo en la siguiente forma. En la Sección 2 se presenta en forma descriptiva la estrategia de globalización de búsqueda lineal exacta en el contexto de la función cuadrática matricial. En la Sección 3 se propone un algoritmo cuasi-Newton global para resolver la ecuación (1). En la Sección 4, bajo ciertas hipótesis, se demuestra que la búsqueda lineal no afecta la tasa de convergencia del algoritmo cuasi-Newton global. En la Sección 5 se analiza numéricamente el comportamiento global del algoritmo propuesto. Finalmente, en la Sección 6 se presentan algunos comentarios finales y propuestas de trabajos futuros sobre el tema.
2. Una estrategia de búsqueda lineal exacta
En el caso de un campo vectorial
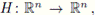una forma de globalizar el método de Newton para resolver un sistema de ecuaciones no lineales, H(x) = 0, consiste en combinarlo con una estrategia global para optimización irrestricta ([6], [20]). En efecto, independientemente de que el vector x esté o no próximo a la solución x* del sistema, una forma razonable de aceptar la iteración siguiente xk+1 es exigir que ||H(xk+1)|| sea suficientemente menor que ||H(xk)|| para alguna norma conveniente. Exigencia que también es hecha cuando se trata de minimizar ||H(x)|| , con lo cual se llega a un problema de minimización.
Extendiendo estas ideas al caso de la función matricial
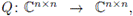donde Q(X) = AX2 + BX + C, se tiene que, si la matriz inicial X0 no está próxima de la solución X* del sistema matricial Q(X) = 0 y Sk es el paso de Newton, entonces en el algoritmo global se busca una aproximación siguiente de la forma X2+1 = X2 + tSk para algún valor de t convenientemente elegido, de manera que Xk+1 sea una aproximación aceptable; en este sentido, buscamos un valor de t tal que ||Q(Xk+1)|| sea menor que ||Q(X2)|| para alguna norma, lo cual conduce a minimizar la función ||Q(Xk + tSk)|| para alguna norma conveniente. Este problema es equivalente a minimizar g(t) = ||Q(Xk + tSk)||2 .
Por conveniencia para el problema matricial, en [10] se considera la norma de Frobenius en la definición de la función g, ya que
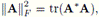para cualquier
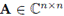. En efecto,
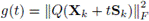es el polinomio de cuarto grado en la variable t
donde
Analicemos el polinomio g(t) dado por la ecuación (2)
Si Y = 0 entonces
en consecuencia, g(t) = α(t - 1)2. En este caso, g(t) alcanza su mínimo global en t = 1, con lo cual Xk+1 es el paso de Newton estándar.Si a = 0 entonces Xk es un solvente de Q X) = 0.
Se puede suponer que Y > 0 y α > 0, con lo cual g'(t) es un polinomio de cuarto grado que tiene a lo más dos mínimos, de los cuales uno es el global. Las raíces de g'(t) que corresponden a los puntos críticos de g son las de la ecuación
g'(t) = 4Yt3 - 3//t2 + 2(a + //)t - 2a = 0. (3)
Para determinar el número de posibles raíces reales positivas y negativas de g'(t), se analizan, siguiendo la Regla de signos de Descartes, los cambios de signo de los coeficientes del polinomio g'(t) y los cambios de signo de los coeficientes del polinomio g'(-t), respectivamente.
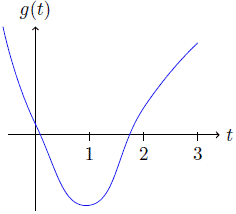
1. Si β > 0 entonces los coeficientes del polinomio g'(t) tienen 3 cambios de signo, es decir, g'(t) tiene una o tres raíces reales positivas. Por otro lado, los coeficientes del polinomio g'(- t) no tienen cambios de signo, es decir, el polinomio g'(t) no tiene raíces reales negativas. Por lo tanto, los puntos críticos del polinomio g’(t) son positivos (Figura 1).
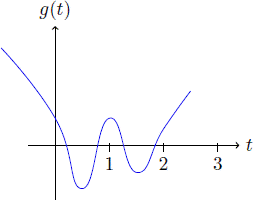
2. Si β = 0 entonces los coeficientes del polinomio g'(t) tienen un cambio de signo, es decir, g'(t) tiene una raíz real positiva. Por otro lado, los coeficientes del polinomio g'( - t) no tienen cambios de signo, es decir, el polinomio g'( t) no tiene raíces reales negativas. Por lo tanto, el polinomio g( t) tiene un único punto crítico real positivo (Figura 2).
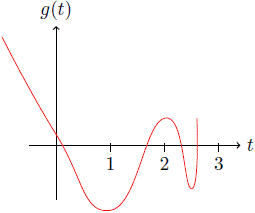
3. Si β < 0, debemos tener en cuenta el signo de a + β. Cálculos sencillos permiten verificar que independientemente del signo de α + β, los coeficientes del polinomio g'( t) tienen un cambio de signo (una raíz real positiva), y los del polinomio g'( - t) tienen 2 cambios de signo (2 raíces reales negativas o ninguna). (Ver Figura 3).
Por otro lado, evaluando g' en 0 y en 2, se tiene
De ahí que g'(t) tiene al menos un cero en (0, 2). Para verificar que en efecto este cero es un minimizador de g, se consideran los siguientes casos para el polinomio g'(t) .
1. El polinomio g'(t) tiene un cero real y un par de ceros complejos conjugados; en este caso, tal cero pertenece al intervalo (0, 2); y corresponde al minimizador global del polinomio g(t) . En la Figura 4, se ilustra este caso.
2. El polinomio g'(t) tiene 3 ceros reales y, por el cálculo diferencial tendríamos que dos de ellos corresponden a minimizadores de g y el otro es un maximizador. Se debe verificar que por lo menos uno de los minimizadores pertenezca al intervalo (0, 2). Una vez hallados y ordenados los ceros de g'(t), se concluye a partir de (4) y (5), que el primero y el último corresponden a los minimizadores de g(t); si estos minimizadores pertenecen al intervalo (0, 2) (ver Figura 5), entonces el minimizador buscado será aquel donde g alcance su menor valor. En caso contrario, es decir, si el tercer cero es mayor que 2 (ver Figura 6), entonces se tiene que el minimizador buscado será el correspondiente al primer cero de g'(t), ya que este pertenece al intervalo (0, 2).
Por lo anterior, el valor óptimo de t en la búsqueda lineal corresponde al minimizador de la función g, y su cálculo implica resolver el siguiente problema de minimización exacta:
Observación: es importante notar que este tipo de búsqueda lineal exacta requeriría, en el peor de los casos, de 3 evaluaciones de la función g, lo cual marca una gran diferencia con la estrategia de búsqueda lineal inexacta [6] que requeriría de muchas más evaluaciones para encontrar un valor de t aceptable. Esto justifica el por qué usar una búsqueda lineal exacta en lugar de una inexacta.
3. Propuesta algorítmica
Como alternativa al alto costo computacional del método Newton-Schur, tradicionalmente usado para resolver la ecuación (1), se propone en [16] un algoritmo cuasi-Newton local cuya iteración básica, a partir de una matriz inicial X0, es la siguiente:
Además, en [16], se demuestra que este algoritmo es local y hasta cuadráticamente convergente. Para mayor claridad en la lectura de este documento, en particular del Teorema 4.1, listamos a continuación dichas hipótesis:
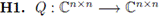es Fréchet diferenciable en un conjunto
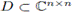abierto y convexo.
H2. Existe X* ∈ D tal que Q(X*) = 0.
H3. La matriz 2AX* + B es no singular y
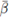es la norma de su inversa.
H4. Existe θ ∈ [0,1] tal que
En esta sección se presenta una globalización del algoritmo anterior. Para ello, se incorpora a dicho algoritmo una estrategia de búsqueda lineal exacta análoga a la usada en [10], la cual se describe detalladamente en la sección anterior. Además, se hace una modificación de la alternativa usada en [15] para evitar la búsqueda lineal cerca de la solución.
En el Algoritmo 1 la expresión Res(Xk) es una medida relativa del error en ||Q(Xk)||F , y es definida como en [10] por
La condición en el Paso 3 es análoga a la usada en [15], y permite decidir en qué caso no es necesario hacer búsqueda lineal.
4. Análisis de convergencia
En esta sección se demuestra que la estrategia de búsqueda lineal exacta no afecta la tasa de convergencia del método cuasi-Newton propuesto en [16].
Teorema 4.1 (Convergencia). Si
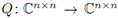es una función cuadrática matricial que satisface las hipótesis H1 a H4, y {Xk} es la sucesión generada por el método cuasi-Newton local (7), entonces la sucesión generada por
también converge a X* con orden 1 + θ, θ ∈ [0,1],
Demostración. Por hipótesis y por Teorema 3.2 de [16], para µ > 0 y θ ∈ [0,1], se satisface que ||XK+1 - X* || < µ ||XK - X*||1+ θ . Equivalentemente,
donde Δk = XK - X*. Debido a que XK está en la región de convergencia de X* entonces se satisface que
para cualquier θ ∈ (0, 1) . Además, Sk = Xk+1 - Xk = Δk+1 - Δk . A partir de esta igualdad, de (10) y (11) se tiene
Q(X + S) = Q(X) + LX(S) + AS2, con lo cual,
De
se tiene
y por (13),
En forma análoga,
Por otro lado, se sabe que en la búsqueda lineal exacta el tamaño de paso t es el minimizador global del polinomio
entonces,
Usando (10), (13), (14) y (17) en (16), se tiene
Por lo tanto,
Usando (18), la definición de O grande, (12) y propiedades de la norma matricial, se tiene que existen constantes positivas
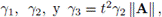tales que
donde γ es una constante positiva. De (15),
para alguna constante p.
Como la derivada de Fréchet de Q es no singular en la solución X*, entonces ||Q( Xk )|| ≠ 0. Tomando recíprocos en (20), se obtiene
Multiplicando (19) por
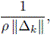se tiene
donde
Luego
con
Por lo tanto,
Luego, usando las actualizaciones (7) y (9), se tiene
Aplicando la desigualdad triangular y usando (10), (12) y (21), se obtiene
Por lo tanto, la sucesión
converge con orden 1 + θ a X*.
5. Pruebas numéricas
En esta sección se analiza numéricamente el comportamiento del Algoritmo 1 (Método cuasi-Newton global) propuesto en la Sección 3. Para ello se consideran tres problemas, entre los cuales uno es una aplicación a un sistema masa-resorte amortiguador ([9], [16]), y otro es un problema de matrices de Hilbert [15].
Con el propósito de comparar el desempeño global de nuestra propuesta algorítmica, se implementa también el algoritmo global de Newton-Schur propuesto en [10]. Además, para apreciar la ventaja de tener un algoritmo global frente a uno local, se implementa el algoritmo local cuasi-Newton [16]. Para mayor claridad en la lectura del documento, se presentan a continuación estos algoritmos.
El Algoritmo 3 encuentra Sk en cada iteración mediante la solución de la ecuación matricial (2AXk + B)Sk = -Q(Xk). Con esta estrategia, se obtuvo una reducción en el costo computacional respecto al Algoritmo de Newton -Schur [16].
Se escriben los códigos de los algoritmos y de las funciones que definen los problemas en MATLAB® y se realizan los experimentos numéricos en un computador Intel (R) Core (TM) i5-3450 de 2,8 GHz.
Las matrices iniciales son de la forma
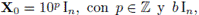donde In denota la matriz identidad de orden
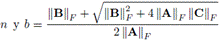es la constante dada en [5]. Además, para el Problema 1 se consideran matrices iniciales X0 = r K, con
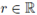y
Para el Problema 2 se consideran matrices iniciales X0 = Cm, con m = 3, 4, 5, 6, donde C es la matriz constante de la ecuación cuadrática a resolver.
Se declara convergencia en los algoritmos cuando
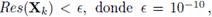y divergencia si el número de iteraciones es mayor que Nmax = 100.
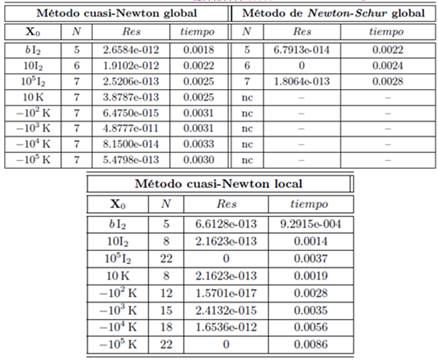
A continuación, se describe cada problema y se presentan los resultados en sendas tablas que tienen la siguiente información: matriz inicial utilizada (X0); número de iteraciones (N); valor de Res definido por (8) y el tiempo de ejecución medido en segundos (tiempo). Para medir el tiempo y quitar el efecto aleatorio de los computadores multitareas se realiza el promedio de tiempo obtenido al ejecutar 100 veces el algoritmo con la misma matriz inicial.
Problema 1. Calcular un solvente de Q(X) = AX2 + BX + C = 0 [10], donde
La ecuación tiene dos solventes reales
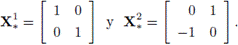
Para este problema se observa el excelente desempeño del método cuasi-Newton global frente al método de Newton-Schur global. Además, se nota la ventaja del algoritmo global propuesto frente al algoritmo local en cuanto al número de iteraciones. En cuanto al tiempo de ejecución de los algoritmos, se observa un comportamiento similar en los casos donde se obtiene convergencia. Los métodos utilizados que convergen lo hacen al solvente
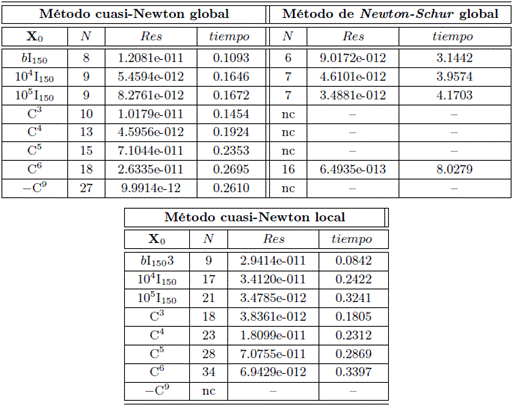
Problema 2. Sistema masa-resorte amortiguador conectado ([9], [16], [18], [24]).
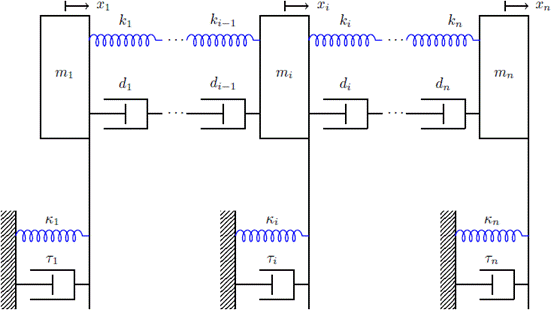
En este problema se considera un sistema masa-resorte amortiguador [25], donde la masa i-ésima de peso mi está conectada a su (i + 1) vecino por un resorte y un amortiguador con constantes Ki y di, respectivamente. La masa i-ésima también está conectada a tierra por un resorte y un amortiguador con constantes Ki y TI, respectivamente (ver Figura 7). La vibración de este sistema está descrita por una ecuación diferencial de segundo orden
donde A = diag(m1,..., mn) es la matriz de las masas, B = tridiag(-Ti, 3Ti, - Ti) es la matriz de amortiguación y C = tridiag(-Ki, 3Ki, -Ki) es la matriz de rigidez, respectivamente.
En las pruebas numéricas, se toma n = 150, mi = 1, para todo i, los resortes y los amortiguadores con un mismo valor constante; es decir, Ki = K = 5 y Ti = T =10, para todo i, excepto B(1,1) = B(n,n) = 2T = 20.
Para las diferentes matrices iniciales, se obtiene convergencia del algoritmo propuesto. En cuanto al tiempo de ejecución, tenemos que en el caso de convergencia en los métodos globales el algoritmo propuesto emplea aproximadamente el 5 % del tiempo que usa el Newton-Schur global, mostrando un excelente desempeño. Además, se aprecia la ventaja de un algoritmo global frente a uno local en cuanto a convergencia se refiere, pues en la mayoría de los casos el número de iteraciones de la propuesta global es cercano a la mitad de las iteraciones empleadas por el algoritmo cuasi- Newton local, y hay un caso en el que el algoritmo local no converge.
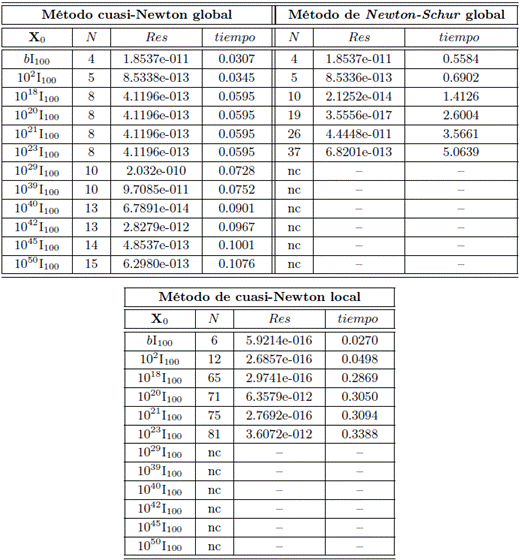
Problema 3 (Matrices de Hilbert)
Calcular un solvente de Q(X) = AX2 + BX + C = 0 ([12], [15]), donde A = I100, B = I100, C = -(H2 + H), y H = (hij), con
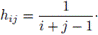
En este problema es en donde mejor se aprecia el impacto en convergencia del método cuasi-Newton global frente al método cuasi-Newton local, así como el excelente desempeño frente al método de Newton Schur global. También se observa el mejor comportamiento del método cuasi-Newton global frente al Newton Schur global en cuanto a tiempo de ejecución, pues la nueva propuesta algorítmica usa aproximadamente un 5 % del tiempo del método Newton Schur global para matrices iniciales donde hay convergencia. Además, la propuesta algorítmica converge en todos los casos considerados.
6. Comentarios finales
Motivados por las bondades de disponer de un algoritmo global frente a uno local [6], y por el buen desempeño local del algoritmo cuasi-Newton que se propone en [16] para resolver la ecuación cuadrática matricial frente al tradicional método de Newton-Shur [10], en este artículo, se presentó una globalización del algoritmo cuasi-Newton basada en la incorporación de una estrategia de búsqueda lineal exacta análoga a la usada en [10] para el método de Newton-Schur.
Se demostró que la estrategia de globalización no interfiere en la tasa de convergencia obtenida para el algoritmo cuasi-Newton, y pruebas numéricas preliminares muestran el buen desempeño del algoritmo global propuesto frente al algoritmo global de Newton-Schur y al algoritmo cuasi-Newton local.
Finalmente, en búsqueda de ampliar el espectro de traba jo con respecto a la ecuación cuadrática matricial y la aplicación del algoritmo global propuesto, pensamos que vale la pena usarlo en la solución de problemas prácticos, ampliando de esta manera el alcance numérico del algoritmo. Por otro lado, sería muy útil usar el algoritmo globalizado para resolver el problema de los valores propios cuadrático [23], que surge en muchos problemas de ingeniería, y que dio origen a la mayoría de desarrollos teóricos de la ecuación cuadrática matricial.
