1. Introduction
The chained hollow brick masonry infill walls, rigidly bonded to their surrounding frame, are widely used in many countries of the world, especially in our country, and cannot be removed in many processes of execution of reinforced concrete buildings. To know the behavior of these walls in buildings exposed to earthquakes, many researchers and specialists in this field have carried out a lot of experiments several decades ago [1,2] where the results of experiments have been compared to the damage caused by earthquakes. There are also new experimental studies such as [3-6].
These walls are usually neglected in the modeling process of reinforced concrete buildings because they are considered non-structural elements. Contrary to what has been proven from the damage recorded by previous earthquakes, they are characterized by a behavior that can lead to a radical change in the general behavior of the building in front of the seismic stresses even if they are of moderate intensity. The infill walls can lead to the collapse of buildings in many cases, or cause great material and economic losses [7,3].
Masonry infill walls are commonly used as interior and exterior walls in the construction of reinforced concrete buildings as well as metal buildings, due to their isolation and distribution functions. Multiple earthquakes have shown the extent of damage these walls can cause when the aforementioned buildings are exposed to seismic loadings like the short column phenomenon [8,9] and the irregular distribution of the walls [10,11] , as well as the positive role of these walls which can be played, by increasing the rigidity of buildings as well as seismic energy dissipation.
In addition to the seismic behavior of buildings influenced by chained masonry infill walls, these walls are considered to be an important factor in the collapse of reinforced concrete buildings, which prompted researchers to adopt new methods to study the behavior of chained masonry infill walls. The methods based on the lateral displacement can be highlighted It is noticeable that the method of nonlinear static analysis "pushover", which has become more and more a very useful method to have a good knowledge of the seismic behavior of buildings infilled with chained masonry.
Several investigations have demonstrated that masonry infill walls are hard but brittle, making them more vulnerable to major and even moderate earthquakes.
To reduce the negative influence of the masonry infill walls on the behavior of the buildings, it is very important to modeling them in structures to have an adequate design and good structural behavior. The best introduction of masonry infill walls in the simulation phase of reinforced concrete structures allows optimal use of the rigidity of the structure. On the other hand, a poor representation of these walls can cause excessive local damage, leading to the total ruin of the structure. Therefore, it is necessary to present a model for properly study the behavior of infilled frames under seismic loadings.
There are several known methods of representing infill walls, and they can be summarized in three approaches known to various researchers interested in this subject [3].
The first approach is the macro-model based on the replacement of masonry infills using one (or more) equivalent articulated struts. This technique is most frequently used in the modeling of this type of walls, to perform linear / nonlinear static or dynamic analyzes due to its simplicity and the lower computational effort required. Most technical codes also suggest a macro-modeling approach for the seismic response of infilled-frame structures [12-16].
The second approach treats the masonry infill wall as a continuum, without differentiating between the different components of the wall, given the resistance and equivalent resistance [17,18].
The last of the approaches that is more precise is the micro-model, which is summed up by considering all the details of the masonry infill wall of the mortar, blocks, whether concrete or brick, as well as the interaction between the wall and the surrounding frame [19,16]. In the following section, we have carried out a parametric study by analyzing several models of a two-dimensional multistoried reinforced concrete frame using the nonlinear static pushover method « pushover ».
With SAP finite element software [20], we analyzed the proposed models and compared the results by a critical synthesis to assess the seismic response of these models by varying the position of the chained masonry infill walls.
2. Description of structure
2.1 General details
Through this article, we have studied eight models that represent a two-dimensional frame that is part of a multistoried reinforced concrete building located in northern Algeria.
The frame has six spans with 4.50m for each span length. The storey height is set at 3.06m with nine storeys. For the chained masonry infill walls, we used a double-leaf hollow red brick with the characteristics recommended by the current Algerian masonry code [21]. The mechanical characteristics of the materials used in the analysis of all models are shown in Table 1.
The models studied are bare frame models (100% openings) without infill; a fully infilled frame model (0% openings), plus six partially infilled frame models with 50% of chained masonry with variation of infill position in chained masonry, as shown in Figure 1. The elements constituting the frame to be analyzed are as follows:
The sections of the columns are (550x550) mm for the first three levels; (500x500) mm for the next three levels, and (450x450) mm for the last levels.
The section of the beams is (300x400) mm; it is the same for all storeys.
The "Pushover" nonlinear static analysis method is based on the structural performance of buildings exposed to seismic loadings. This method is mainly based on the controlled displacement approach using a plastic factor, which measures the degree of plasticization of the building elements.
It considers nonlinear elastoplastic behavior with progressive increase of the lateral loadings. The model studied must consider the inelasticity of the material due to stress states and it must offer the possibility of progressively monitoring the plasticization of each element under increasing intensity of seismic loading.
The models are analyzed using the finite element software SAP [20], by using the nonlinear static "Pushover" method, which represents a nonlinear analysis method and can give more precisely the seismic behavior of structures.
The parameters used to judge the seismic response of these models are vibration period, base shear, lateral displacement and stiffness.
The purpose of a pushover analysis is to assess the expected performance of a structure by estimating its demands for resistance and deformation during an earthquake using nonlinear static analysis and comparing these demands with the capacities of the building at appropriate performance levels. Assessment is based on monitoring the most important performance parameters, including lateral displacement, elastic base shear, initial stiffness and ultimate base shear. Nonlinear Pushover Analysis can be viewed as a method of predicting demands in terms of seismic forces, which approximates the redistribution of internal forces that occurs when the structure is subjected to inertial forces to which linear structural behavior elastic cannot resist.
Pushover method analysis can be performed by controlling the force or displacement depending on the nature of the actual load and the expected behavior of the structure. Controlled force is useful when the load is known (such as gravity loadings) and the structure is believed to be able to withstand that load. The second procedure, displacement control, should be used when the loads have not been evaluated beforehand (for example, in the case of seismic loading), i.e., when the amplitude of the applied load is not known in advance, or when it can be predicted that the structure will lose strength or become unstable.
a. Modeling of proposed frames: Regarding the modeling process, we used the pushover method, using the SAP finite element software [20], which uses the best-known method in most structural analysis software. Where we have considered 2D bares frames with the previously mentioned dimensions, the period of the buildings was considered one of the most important criteria for studying the seismic behavior of these buildings, with the following factors being taken into account, namely, base shear, lateral displacement and stiffness.
In addition to the geometric and mechanical characteristics of the materials and sections of elements constituting these frames, used and mentioned in the general details section.
To model the chained masonry walls, we relied on the "shell" finite element, recommended by the SAP software to represent the walls. The element "shell" represents both the slab and the wall.
We determined the geometrical characteristics of a wall element composed of two pieces of hollow brick widely used in Algeria with a solid element without voids, keeping the length and width of the element and extracting the appropriate thickness for a solid element with the same properties of the hollow brick.
When we obtained the appropriate thickness, we modeled the wall using the nonlinear multilayer element by the finite element software SAP 2000 [20].
b. Validation of the model: To validate the models studied by the SAP software [20], we used the famous SEISMOSTRUCT software [22], which offers a large capacity to model the infill masonry walls. We have modeled the bare and fully infilled frames with the thickness mentioned above. After that, the same frames were modeled using SAP software, and compared them with the results given by SEISMOSTRUCT software [22], which showed a great convergence between the two software results, regarding the period of building, which allowed us to use the models proposed, and generalize them to additional models with the factors mentioned previously, and always according to the period of the building.
3. Results and discussions
a. Effect of various random locations of the walls on the period of vibration
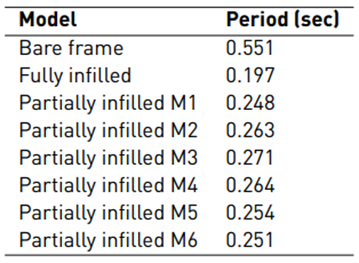
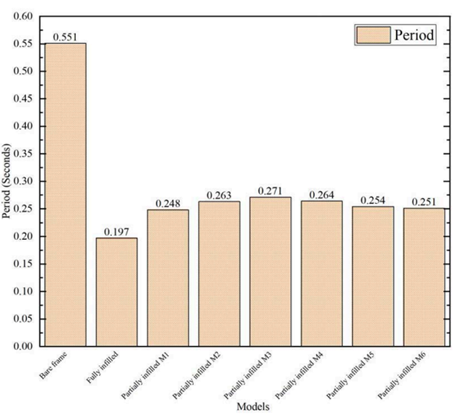
Analyzing Table 2 and Figure 2, we can first say that the role values of the fully infilled model recorded a significant decrease compared to the bare frame model by more than 64%, which is a clear indication about the role played by the chained masonry walls to improve the resistance of the reinforced concrete frame.
Secondly, after infilling the frames by 50 percent randomly, we noticed through the results obtained that the model M1, recorded the lowest value for the period, followed by M6, then M5, then M2, then M4 and finally M3, but with relatively close values.
For example, if we compare models M1 and M3, we find a slight difference that does not exceed 8 percent. This indicates that changing the location of the walls randomly while adhering to the same proportion of chained masonry does not significantly affect the period of the partially infilled frame. However, if we compare the model that provides the highest value of the period with the bare frame, we find a difference that cannot be underestimated, as it exceeded 50 percent, which clearly shows how the presence of chained masonry walls affects the period of the frame in the modeling process.
We observed a great convergence between the different partially infilled models, which clearly indicated that the random distribution of the position of the infill walls did not significantly affect the seismic behavior of the reinforced concrete frames.
Regarding the Pushover curve, we can say that the latter did not significantly affect the seismic response of these types of frames, while neglecting the slight change that occurred between the different models that we analyzed.
b. Effect of various random locations of the walls on the pushover curve
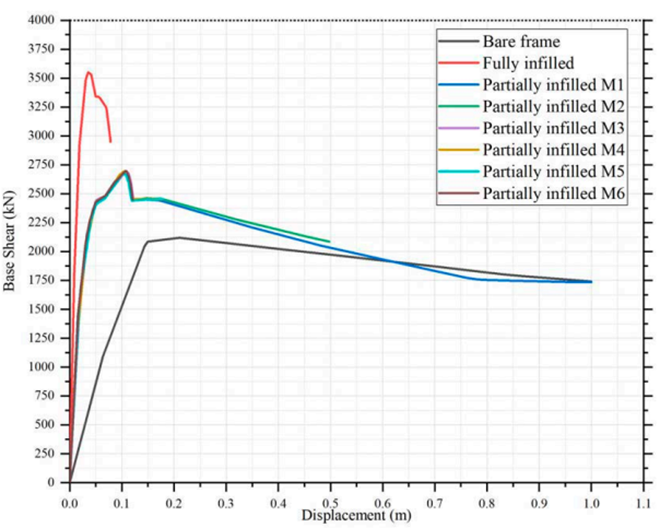
Based on the analysis of Figure 3 and the results contained in it, we noticed that the bare frame showed the lowest base shear value with the largest lateral displacement value compared to the fully infilled frame which showed a greater value for the base shear and the lowest value for lateral displacement, which clearly indicates the large difference between them due to the presence of chained masonry walls, which greatly improved the frame's seismic response ability.
As for the partially infilled frames, their results were relatively close, which means that the random distribution of the chained masonry walls does not affect in a significant percentage the seismic performance of this type of frame. If we want to arrange these frames regarding lateral displacement, they will be as follows: first, the model M4, followed by M2, then M1, then M6, then M5, and finally M3.
We can say that the latter did not significantly affect the seismic response of these types of frames, while neglecting the slight change that occurred between the different models that we analyzed.
c. Effect of various random locations of the walls on the elastic displacement
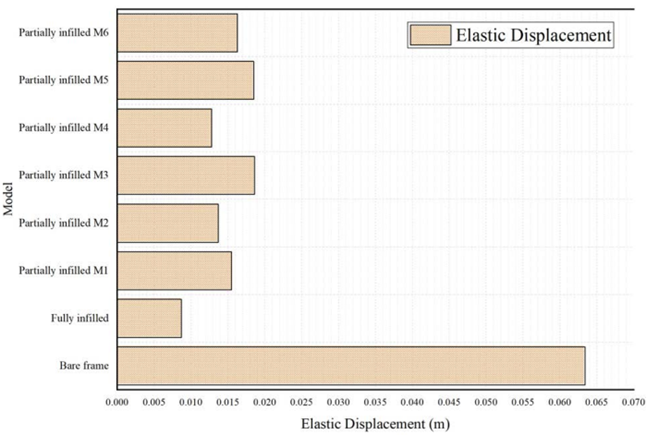
Analyzing Figure 4 and Table 3, which contain a comparison of the various proposed models through the lateral displacement parameters, we can observe the large displacement recorded by the bare frame compared to the fully infilled frame, which indicates the effect that the chained masonry walls have on the behavior of the frame towards seismic loadings.
On the other hand, if we compare the partially infilled frames, we can say that model M4 recorded the lowest value for lateral displacement compared to the rest, followed by M2, then M1, M6, M5, and finally M3.
If we rely on the model M4, which recorded the lowest value and considered it as a reference for the recorded increase, we can say that M1 recorded an increase of 17.42%, 6.57% for M2, 31.18% for M3, 30.81% for M5, and 21.47% for M6. Accordingly, we can say that the models recorded relatively close proportions, if we exclude M2.
We can say that the latter recorded a significant effect on the seismic performance of the models studied.
Almost the same has happened with the elastic base shear, which is mainly related to the lateral displacement in the elastic domain, that we noticed a slight difference between the different models.
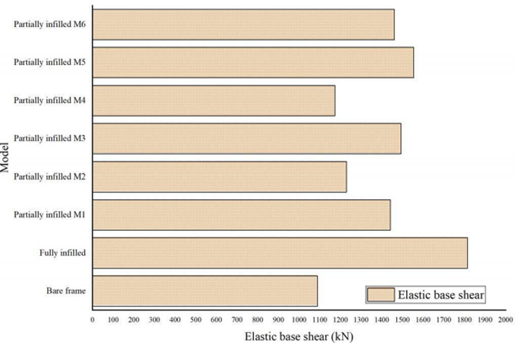
d. Effect of various random locations of the walls on the elastic base shear
Depending on Figure 5 and Table 4, we can read the recorded results as follows:
Firstly, the fully infilled frame showed the largest value of the elastic base shear compared to the bare frame, indicating that the presence of chained masonry walls had a positive effect on the seismic response of the reinforced concrete frame.
Secondly, without taking the two frames that are fully infilled and as well as the bare one, we can compare the partially infilled frames, where we can notice that the model M5 recorded the largest value for the elastic base shear compared to the rest.
If we rely on the model M4, which recorded the lowest value and considered it as a reference for the recorded increase, we can say that M1
By comparing the partially infilled models, we can say that the values are relatively close and do not constitute a significant influence on the seismic behavior of this type of reinforced concrete frame.
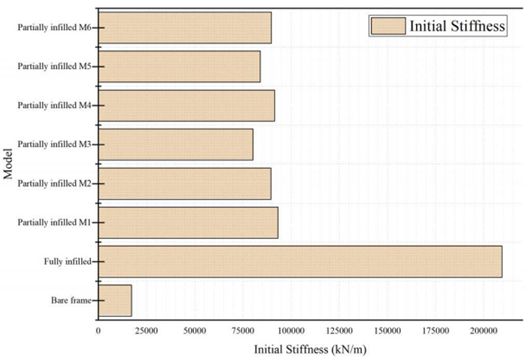
e. Effect of various random locations of the walls on the initial stiffness
Figure 6 and Table 5 group together the results obtained regarding the initial stiffness.
Regarding the fully infilled frame and the bare frame, we noticed that the fully infilled frame recorded the highest value of the initial stiffness as this value increased more than 12 times compared to its bare counterpart. This confirms that the presence of chained masonry infill walls in the modeling process greatly contributed to increasing the initial stiffness of the reinforced concrete frame.
For partially infilled frames, we can read the maximum value recorded by the model M1, followed by M4, then M6, then M5, and finally M3.
And if we consider the M3 model, which recorded the lowest value of the initial stiffness of all partially infilled frames, as the reference model, then we clearly see that the M1 model registered an increase of 13.91 %, M2 of 10.37%, M4 of 12.17%, M5 of 4.47% and M6 of 10.60%. If we exclude the M5 model, we see that the values are quite close, which generally indicates the slight effect marked by the random distribution of the chained masonry infill walls, but on the condition that 50% of the infill process is respected. However, it remains to be said that this slight difference can lead to remarkable damage.
We can say that there is a slight difference between the models, which indicates the differential effect of the random distribution of the position of the chained masonry walls.
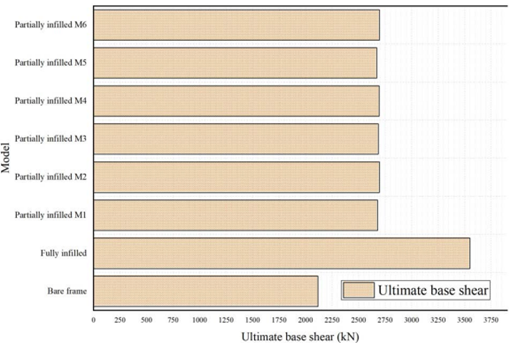
f. Effect of various random locations of the walls on the ultimate base shear
Based on Figure 7 and Table 6, which represent the results of the proposed models with respect to ultimate base shear, we can read the following:
For the bare frame, we note that it recorded the lowest value compared to the fully infilled frame. This is mainly due to the introduction of chained masonry infill walls in the modeling process of the frame, which leads us to say that the presence of these chained masonry walls deeply affected the seismic response of the frame, and improved its seismic performance. A fully infilled frame marked an ultimate base shear of 40% compared to the bare frame.
If we come back to observe partially infilled frames by 50%, their results were relatively close, according to the results recorded in the table cited above. We can classify the partially infilled frames regarding the ultimate base shear as follows: the model M6, followed by M2, then M4, then M3, then M1, and finally M5. It can therefore be said that the random change in the position of the chained masonry infill walls did not significantly affect the seismic behavior of the partially infilled frames, if the same infill rate and the same dimensions were preserved.
We could conclude that the effect of randomization of the position of the chained masonry walls was not significant.
4. Conclusions
After completing the analysis of the different models offered, we clearly noticed the considerable influence marked by the presence of the chained masonry walls on the seismic behavior of the reinforced concrete frames, when we modeled them directly with the rest of the elements constituting the frame, which clearly indicated that there is no doubt that the indirect insertion of these walls or neglecting them in the modeling process can lead to false exploitation of the seismic behavior of reinforced concrete buildings. This greatly encourages all designers to take the chained masonry walls into consideration in the various modeling processes to better understand the response of multistoried reinforced concrete buildings when exposed to seismic loadings.
Finally, considering all the criteria, we can say that the random distribution of the position of the chained masonry infill walls had a slight and different effect on the seismic performance of the reinforced concrete gantries. However, considering the losses that could be caused to such buildings, we cannot neglect this effect, considering the importance of the building, and its location in the seismic zone, as well as its constituent elements.