INTRODUCTION
The theory of value seeks to explain the way prices function as a coordination mechanism of market societies. Schumpeter (1954) was the first to consider that this theory could have both a real and a monetary approach. The real approach excludes money in order to consider only real economic magnitudes in its analysis and is the dominant approach that has been more widely applied. The monetary approach, on the other hand, is less well known and has not been applied to the same extent. It can be classified into two categories: one that considers only monetary variables, and another that considers both real and monetary variables. Henceforth we will call the former the strictly monetary approach and the latter the monetary approach.
The validity of the real approach's method for achieving the goals of the theory of value has been widely criticized, so it is surprising that it still has such preeminence in economics. This could be explained, in part, by the lack of knowledge of the monetary and strictly monetary approaches to theories of value, since these have been developed more recently, and the lack of analysis of their scope and limits in comparison with their real counterpart. This paper aims to fill this gap by reviewing these models and analyzing their scope and limits as an alternative to real analysis.
The paper is organized as follows: the next section defines the main objective of theories of value in general terms (valid for any theoretical framework) and in detail (to clarify all its logical implications concerning money) and outlines the limits of the real approach and the strictly monetary approach as theories of value. The third section examines the limits of the monetary models developed within the neoclassical framework and, in the fourth section, those developed within the classical-Marxian tradition. Finally, the fifth section presents the conclusions.
PURPOSE OF THE THEORY OF VALUE AND LIMITS OF THE REAL AND STRICTLY MONETARY APPROACHES
The general economic problem that any social system faces consists of how to determine what, how, how much, when, and where people will produce and consume at any given moment. In market societies, these issues are decided by all economic agents in a decentralized manner without any a priori coordination. The economy is organized in markets so individuals can specialize and exchange the product of their economic activities, and the adjustment of prices is expected to prevent these activities from being systematically incompatible (Klimovsky, 2000).
This kind of social system raises several questions. For example, under what conditions can the price mechanism coordinate all economic activities? Are markets self-regulating or do they always tend towards crises? How do different kinds of incomes evolve? And ultimately, will this economic system be able to solve the various problems that humanity currently faces (such as environmental problems, economic inequality, etc.)?
Theory of value aims to answer these questions from a general (and therefore abstract) standpoint, first analyzing the logical conditions under which prices can function as a coordination mechanism of market societies, and then analyzing the logical implications that this functioning may have concerning other aspects of interest such as those just mentioned (environmental problems, economic inequality, etc.).
Now, assuming a veil of ignorance of the current state of theories of value in all their approaches, let us consider the minimum theoretical aspects that a theory of value should have to satisfactorily explain the price system working in market societies.
First, an explanation must start from a disaggregated description of the economy in terms of individuals and commodities. This is because aggregate analysis of the economy eliminates the coordination problem that the price mechanism must solve, and the theory of value must explain1.
Secondly, the interdependent relations that exist between consumption and production activities must be made explicit, since, if these relations are not specified, it will never be possible to know whether prices can or cannot be an effective mechanism for coordinating these activities.
Third, the minimum institutional framework that allows individuals to act in market societies must be specified. Within this institutional framework, a fundamental element is money and the monetary system since a barter system is not compatible with decentralized exchanges.
Next, the mechanisms by which the market economy works (how supply, demand, prices, and exchanges are determined and adjusted) must be specified in detail. It is important to emphasize that, in market societies, economic activities such as exchanges, production, and consumption take place continuously, regardless of whether the economy is in equilibrium or not.
And finally, it is necessary to show the conditions under which price adjustment can, or cannot, regulate disequilibrium. In other words, the theory must identify the conditions under which the adjustment process occurring in the model is stable or non-explosive, in the sense that any imbalance that appears decreases or, at least, does not increase over time.
Note that once these requirements are met, the other problems posed by this type of social organization, such as wealth distribution, environmental problems, etc., can then be analyzed. It is naïve to try to give a scientific answer to these normative and practical aspects without first having a logically coherent theory of value. Hence the importance of theories of value for the science of market societies.
Limits of the real approach to the theory of value
The canonical models of the real approach to the theory of value are the neoclassical general equilibrium model (Arrow & Debreu, 1954) and the classical-Marxian production prices model (Sraffa, 1966), as well as the neoclassical disequilibrium model of Walrasian tâtonnement (Arrow et al., 1959) and the classical-Marxian disequilibrium tâtonnement models of gravitation2 (Boggio, 1985).
Assuming that the main results of these models are known to the reader3, it can be said that they only fulfill the first and second requirements mentioned above, but not the third, fourth, or fifth, because 1) the exclusion of money implies that the decentralized functioning of markets be left aside (Ostroy & Starr, 1974), so the prices explained by this approach do not result from market economies; 2) the positive price of money cannot be explained by the theory of value (Benetti, 1990), so the results obtained by this approach cannot be attributed a posteriori to a monetary economy; 3) except in very particular cases, money is not neutral (Lagos & Wright, 2005), so the results obtained by this approach will not generally be equivalent to those resulting from monetary economies either; and 4) the tâtonnement process depends on a centralized mechanism that is also incompatible with the market society. For all these reasons, it can be concluded that the real approach to the theory of value is logically incapable of explaining its object of study.
Limits of the strictly monetary approach to the theory of value
The strictly monetary approach is formed by a small group of heterodox monetary theories that all construct a theory of value without reference to the real sector, namely, the theories proposed by Benetti and Cartelier (1980), Aglietta and Orléan (1982, 2002), and Cartelier (2018).
The starting point for the strictly monetary approach was Benetti and Cartelier's 1980 study. In this study, they take on the problem posed by the theory of value directly and try to find a solution in exclusively monetary terms. This, because they consider commodities to be of no analytical interest due to the fact that 1) they are the result and not a condition of market relations (they criticize the nomenclature hypothesis which presupposes the existence of a commodity space independent of the functioning of the market); and 2) capitalist production activities are inaccessible to economists because they are carried out in the "secret laboratories" of capitalists, so this knowledge could not be obtained even if it were of interest to economists.
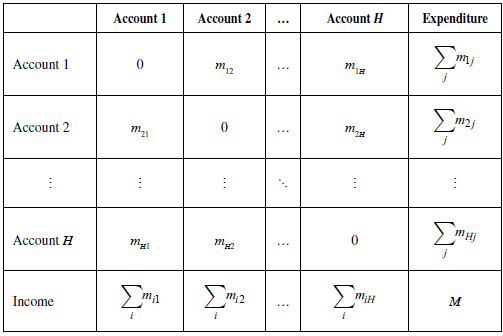
For this reason, this approach conceives market societies as a system of individual monetary accounts, interrelated by the monetary payments that occur between them, and which are expressed analytically through the following matrix (Table 1).
Where ≥ 0 (with i, j = 1,..,H) is the amount of money that account i pays to account j, as a counterpart of the purchase of a commodity on a given date. If money is fiat, money enters the matrix in the form of credit offered to individuals by the monetary authority and leaves it when individuals repay this debt. On the other hand, if money is anchored to the quantity of a standard commodity, then the monetary institution sets a legal price for this commodity, and money enters the payment matrix when individuals sell their stocks of this commodity to the monetary institution and leaves when they buy these stocks (Aglietta & Cartelier, 2002). Thus, the monetary authority can control this quantity by manipulating the monetary interest rate, in the first case, or the legal price of the standard commodity, in the second case.
In a credit market economy, individuals borrow money to finance their expenses before obtaining income from the sale of their products. To calculate the amount of a requested loan, individuals rely on their income expectations. One of the characteristics of disequilibrium is that not all individual expectations are fulfilled. Therefore, during disequilibrium, there are always individuals who have negative or positive balances of money, with the sum of these balances always equal to zero (since aggregate income is equal to aggregate expenditure, represented in the payments matrix by the letter M).
These balances need to be regulated so that debtors meet their obligations by transferring wealth to creditors (Cartelier, 2009). However, if the punishment of deficit holders is not severe enough, it will discourage surplus holders from keeping their wealth in monetary form, which may unleash inflationary pressure. On the other hand, if the punishment is too severe, it may cause a contraction of aggregate demand, affecting the whole economy (Aglietta & Orléan, 1982, 2002).
Thus, the dilemma that any monetary authority faces is the question of how to formulate balance settlement rules that satisfy these two aspects of the same problem: on the one hand, to avoid a recession crisis by allowing debtors to settle their debt and remain in the system and, on the other hand, to avoid an inflation crisis by giving individuals with a positive balance a return on their balances that satisfies their expectations. The 'viability theory' (Cartelier, 2018) analyzes this dilemma in dynamic terms.
This explanation, while brief, is sufficient to demonstrate that the strictly monetary approach completely satisfies only the first and third requirements mentioned above (namely, disaggregated description and consideration of the institutional aspects of the economy-particularly money-), and the monetary aspect of the second, fourth, and fifth requirements of the theory of value (consideration of the monetary relations of interdependence through the payments matrix, specification of the dynamics in monetary terms and its analysis through the theory of viability). It does not, however, satisfy the real dimension of these last three requirements, since the relations of interdependence that exist between the individual activities of consumption and production are not considered, nor are the dynamics specified in real terms, and the conditions of their convergence to equilibrium are not analyzed.
This is a problem because although the objects of final consumption may be the result of a specific market performance, such objects can only be produced by satisfying the terms of certain technical relations with other objects which are independent of market relations at a given moment in time. The theory of value must explain how the price mechanism can or cannot satisfy the terms of these interdependent relations over time. These terms must be satisfied in order for the productive activities to continue to function. If production activities were to decrease or even cease, this would jeopardize the very existence of society, regardless of the circumstantial objects of final consumption produced in the economy.
In other words, every social system has a set of technically viable productive methods that establish relations between economic objects, the terms of which must be satisfied in order for the objects to be produced. These relations are characterized as real, non-monetary and independent of the social system, and are a fundamental aspect of the relations of interdependence that exist in any social organization and, therefore, are a central part of the coordination problem posed by the functioning of the price system. However, by using a strictly monetary analytical framework which leaves these relations to one side, this approach cannot provide an answer to the problem of coordination, as was later recognized by Benetti and Cartelier (2013). A strictly monetary analytical framework, then, cannot be a coherent approach to the theory of value either.
This section has shown that a coherent approach to the theory of value must be framed in a microeconomic model of disequilibrium, in which the monetary and non-monetary relations of economic interdependence between individuals and their activities are made explicit. This model must also show the conditions under which the price system can (or cannot) coordinate economic activities and their interdependent relations.
THE NEOCLASSICAL MONETARY APPROACH TO THE THEORY OF VALUE
In the neoclassical framework, Patinkin (1959) was the first economist to, correctly and completely, set out the requirements of a research program studying a monetary approach to the theory of value. According to Patinkin, the research must "explain the determination of equilibrium prices in the market", and to do this, researchers must "be interested in presenting first a static analysis of our problem (the nature of the equilibrium position), then a dynamic analysis (the nature of the market forces which bring the economy to equilibrium from an initial position of disequilibrium)" (p. 34).
For this, Patinkin formulates a model of pure exchange (no production), pure cash (no credit), and temporary equilibrium (at each date there are only markets for the goods to be consumed at that date). At the beginning of each period t there is a Walrasian tâtonnement in which an auctioneer adjusts prices, following the law of supply and demand, until a temporary equilibrium is reached. Then, individuals trade in a random sequence until all possible exchanges are exhausted in t and consume the goods in such a way that, at the beginning of the period t + 1, they only have the money they have carried over from the previous period and the endowment of goods they will receive in t + 1.
Patinkin assumes that the utility function of individuals depends on the goods they can obtain in the period and the real stock of money they wish to transfer to the next date. The reason that justifies such a transfer is that individuals do not know what the sequence of exchanges in each period will be, and it is possible that to obtain the goods they want, they will have to buy these before selling their own goods. For this, they will need to have an amount of money available at the beginning of each period that will allow them to finance those purchases.
Patinkin fails to solve his research question because, on one hand, he does not offer any proof of the existence of monetary equilibrium and, on the other, he analyzes equilibrium stability only in the case of a two-commodity economy, which implies that his stability proof lacks generality (Arrow & Hahn, 1971). Moreover, as mentioned above, the Walrasian tâtonnement is incompatible with market economies.
The research program put forward by Patinkin was taken up in its full form by Arrow and Hahn (1971) who used an intertemporal equilibrium analytical framework. That is, they assume that, from the initial date, there are open markets for all goods that will be available in the present and future. At each date, exchanges of (property rights to) goods are admitted, at prices determined by a Walrasian auctioneer, who modifies them following the supply and demand law and forbids consumption activities while general equilibrium is not reached. Once equilibrium is reached, if the process is stable, all markets are closed, and the rest of the time individuals dedicate themselves to fulfilling the commitments assumed during the adjustment process.
The first important problem with this model is that there is no reason to hold fiat money in equilibrium, since when this state is reached there are no more exchanges in the economy, so no individual would accept the holding of fiat money in equilibrium. To avoid this problem, Arrow and Hahn (1971) assume that money has a direct utility for individuals that justifies its holding in equilibrium. The authors recognize that this artifice implies a "bad monetary theory" (p. 339)4.
Under this analytical framework, Arrow and Hahn show that the existence of a monetary equilibrium depends on the same conditions as a non-monetary equilibrium and that a sufficient condition for its stability is that individuals never run out of money at the beginning of each period5.
The Arrow-Hahn model has many other problems which have been pointed out by Fisher (1983) and Benetti (1996), among others. The main problem highlighted here is that their model remains incompatible with market society because 1) it maintains the fiction of the auctioneer and a centralized process to explain the price adjustment, 2) it maintains the need for a centralized mechanism to control (forbid or allow) consumption activities while the adjustment process takes place and 3) it stipulates that exchanges and markets disappear during equilibrium, a strange property for market societies. For all these reasons, it can be said that this model is also contradictory to a monetary approach to the theory of value.
After Arrow and Hahn, the only author who has continued to experiment with Pat-inkin's program in the neoclassical framework is Franklin Fisher. First, Fisher extended Arrow and Hahn's model into production (Fisher, 1974), and a few years later he proposed an entirely new model of a monetary economy under imperfect competition and in an intertemporal disequilibrium framework (Fisher, 1983). In this model, trade, consumption, production, and credit are admitted during the adjustment process, and Fisher also identified the conditions sufficient for convergence to equilibrium.
In Fisher's new model, credit is expressed through bonds that are exchanged in its markets like any other commodity. Bonds can be public (when the issuer is the government) or private. An individual becomes interested in issuing these bonds when they consider that the amount of money they can obtain through them is more convenient than any other form of financing. The government issues or withdraws bonds to control the amount of money in the economy. On the other hand, bonds are demanded not because they generate some intrinsic utility, but because they provide an expected future return.
Given that not all individuals may be able to fulfill the commitments made during disequilibrium, there must be a regulation obliging the defaulting individuals to pay a fine to the injured agent. Fisher recognizes this problem and assumes that such a fine must fulfill the following properties: 1) that the injured agent will not be better off receiving the fine than they would be if they had received that provided by the contract and 2) that the defaulting agent would not prefer to repurchase the contract rather than pay the fine. In addition, he highlights the moral sanction that fraudsters receive in terms of loss of confidence and allocates a necessary last resort for those who cannot pay their fine: prison.
Fisher analyzes the stability conditions of the equilibrium of this economy through the second Lyapunov method. One of the most important conditions he identifies is the "absence of favorable surprises". This condition refers to the fact that, as long as individuals do not make an optimist adjustment to their expectations of the future, the disequilibrium process will follow a path on which their expected utility and profit levels will worsen until equilibrium is reached, so the sum of these levels is used by Fisher to construct a Lyapunov function to prove both stability and the existence of general equilibrium.
To illustrate the implications of this result, let us consider the case of positive excess demand in one of the markets. Individuals realize that there are potential buyers who cannot buy the commodity being sold in this market, so they anticipate that its price will increase, and will try to take advantage of this situation by increasing their current demands, either for consumption or arbitrage, thus increasing the excess demand and raising its price. This pressure will continue until the relative price ceases to provoke an optimistic revision in the expectations of most of the individuals participating in the market. This means that the arbitrage opportunities perceived by these individuals will disappear and they will no longer want to buy the commodity, thereby reducing the excess demand until equilibrium is reached.
And in the case of an excess supply imbalance, individuals realize that there are suppliers who want and cannot sell these goods, and anticipate that their price will decrease, and will try to take advantage of this situation by postponing their purchases (if they have a positive excess demand) or rushing their sales (if they have a negative excess demand), thereby increasing the excess supply and the downward pressure on the price. This pressure will continue until the price decrease ceases to cause an optimistic revision in the expectations of most of the individuals participating in this market, so that they no longer perceive arbitrage opportunities and, as a result, the excess supply will begin to diminish.
Thus, when individuals cease to perceive arbitrage opportunities generated by any disequilibrium, their expected level of welfare worsens because the goods they could not buy will increase in price and those they could not sell will decrease in price, so that in the "absence of favorable surprises" the aggregate level of welfare will decrease until it reaches the level corresponding to the equilibrium state. And using this aggregate level as a Lyapunov function, Fisher shows that ".. .under very general circumstances, economies with rational, arbitraging agents will converge to equilibrium given an assumption of No Favorable Surprise" (Fisher, 1983, p. 91).
This result is the most important so far achieved by the monetary approach of the neoclassical theory of value, due to the general character of the specified economy. However, the model presents two important problems that remain to be solved.
The first problem is that nothing is known about speeds of adjustment. This is important because a stable equilibrium with a very slow adjustment process justifies some sort of government intervention. Secondly, the proof for the existence and stability of the equilibrium is so general that nothing is known about the characteristics of the equilibrium. Thus, even if the equilibrium is stable and the adjustment process rapid, some sort of government intervention is justified if the equilibrium is quantity-constrained, for instance, with underemployment, as Keynes points out.
Therefore, with this model, we find ourselves at almost at the same level of ignorance that the theories of value were intended to overcome. Moreover, if nothing is known about economic equilibrium in terms of its competitive structure or the presence or absence of quantity constraints, less will be known about the other aspects that derive from the theory of value and which are of much more practical interest, such as, for example, the role of the market in economic inequality or the environmental crisis, etc.
THE CLASSICAL AND MARXIAN MONETARY APPROACH TO THE THEORY OF VALUE
The monetary models of the classical-Marxian theory of value have a much more recent history. They began to appear in the 1980s with the emergence of models that tried to formalize classical-Marxian gravitation theory. Broadly speaking, this theory of value postulates that when market prices do not guarantee a uniform rate of profit, they cannot remain fixed, since differences in profit rates will encourage capitalists to transfer their capital from the less profitable sectors to the more profitable ones, thus altering the productive structure of the economy and market prices. This process of adjustment will stop only when the prices that guarantee uniform profit rates (the equilibrium prices of the classical-Marxian approach to the theory of value) are reached.
Although there are differences between Smith, Ricardo, and Marx on this issue, the literature usually encompasses the different formalizations made in this field as gravitation models (Carminati, 1990). Most of them are non-monetary and tâtonnement models. To the best of our knowledge, only three types of gravitation models stand out as being monetary and non-tâtonnement, namely: those of Nikaido (1983; 1985)6, Duménil and Lévy (1983; 1990a; 1990b) and Benetti et al. (2014; 2015).
These three models share the following assumptions: the economy is monetary and bi-sectoral; wages are given and paid ex-ante in physical terms; each branch produces a single commodity with a single method of production, using both goods as productive inputs in fixed proportions and under constant returns to scale. We will now examine the particularities of these three models.
Nikaido analyzes Marx's gravitation theory through two disequilibrium models, the only difference between them is that in one, he assumes simple reproduction, and in the other, expanded reproduction. Despite this difference, both models share the same hypotheses: the accumulation rate of each capitalist is exogenously given (it is zero in the first model and a constant proportion of their income in the second). Nevertheless, the amount of money that capitalists invest in each branch depends on the differentials of their profit rate, where: if the rate of profit is higher in branch 1 than in branch 2, at the next date the amount of money invested in branch 1 will increase at the expense of branch 2 concerning the previous period, etc. The monetary institution is a pure cash system, meaning that the amount of money spent by capitalists in each period is equal to their income at the previous date. Prices are determined by two alternative rules: the rule of temporary equilibrium (supply equals demand on each date) and the following temporary disequilibrium rule: commodity prices are those which match the value of capital with the monetary amount of investment.
The two Nikaido models show that, if the capital composition of branch 1 is lower than that of branch 2, the adjustment processes of both models converge to equilibrium, that is, market prices 'gravitate' to production prices. Otherwise, the process diverges in the sense that market prices move indefinitely away from production prices.
Nikaido's two models have several problems: 1) the hypotheses are quite specific, which shows the narrow limits of his results: his models are bi-sectoral, with only one method of production, no fixed capital, no rent, etc. and it is not evident that generalizing such hypotheses would yield the same results; 2) the absence of a theorized behavior for capitalists that would explain how their consumption and investment decisions are determined; 3) the mechanism of capital mobility lacks micro-foundations (if branch 1 yielded a higher rate of profit than branch 2, and if all capitalists have this information, why do capitalists not invest all their capital in branch 1? Why is there a non-zero investment in branch 2?); 4) both rules for determining prices are incompatible with market societies because they are centralized: the equations system to calculate prices in both rules can only be solved by considering the interdependence relations among the whole economy, and 5) the pure cash monetary system is one of the two extreme cases in which any actual economic monetary system is found7. Therefore, Nikaido's monetary hypothesis is very particular, and there is no evidence to suggest that generalizing it would give the same results.
In Duménil and Lévy's model, they propose an alternative formalization of the Marxist gravitation theory which, in addition to the basic characteristics already mentioned, they set the accumulation rate at zero. However, capitalists allocate their capital in each branch according to the differentials in sectoral profit rates; branch 1 produces a durable good (fixed capital), so now the economy is a joint-production system. The prices of each commodity are set by the capitalists in each branch using the following rule of price adjustment: the price varies in proportion to the difference between the actual and the desired stock of each commodity held by the capitalists in their warehouses; the economy works through a credit monetary system (there is a banking system which captures the savings of consumers and lends to producers at a zero interest rate and according to the differentials of the sectoral profit rates).
The authors show that, under certain conditions which concern the reaction coefficients of prices and quantities, the dynamics of their model converge to production prices. However, in addition to the assumptions criticized above made by Nikaido in his model which this model reproduces, the Duménil and Lévy model has the following two additional problems:
First, the theoretical indeterminacy of their rule of price adjustment. This rule depends on two parameters: 1) the desired stock of goods and 2) the coefficient that relates price variation to the difference between the actual and desired stock of goods. The problem with these two parameters is that both are, on the one hand, arbitrary (in the sense of being theoretically unjustified) and, on the other hand, fundamental to the stability results, which makes their model uninteresting.
And, secondly, the Duménil and Lévy model does not consider the regulation of monetary balances that may appear during disequilibrium, due to the existence of credits in the economy. This situation puts the whole monetary system in conflict, meaning that institutional rules must be specified to allow the settlement of these monetary balances to reestablish ex post the budget constraint of individuals. However, Duménil and Lévy are silent on the matter.
Benetti et al. (2014; 2015) do specify a monetary balance settlement rule in their models. In addition to the basic features already mentioned, these models assume that: 1) capitalists accumulate all their income and reinvest it in their branches (Benetti et al. criticize the mechanism of capital mobility between branches to explain the adjustment of quantities and reject it for lacking micro-foundations); 2) prices are formed by a perfectly competitive market mechanism called the 'Cantillon rule' (under which the prices of each commodity are determined by dividing the quantities of money and commodity brought to the market to be exchanged); 3) the monetary framework is a pure credit system issued by a bank (credit is issued at the producer's request, and the producers commit to reimburse the bank immediately after the exchange); 4) the monetary balances appearing in disequilibrium are settled by the following rule: the capitalist with a positive monetary balance gives his balance to the capitalist in the red in exchange for a basket of commodities whose monetary value is equal to the monetary balance (evaluating the goods at their market prices) and whose physical composition is chosen by the agent with a positive monetary balance.
The authors of this model show that the balance settlement rule can be unfeasible in certain cases, which they call "pathological". But, when these cases are excluded8, the dynamics to which the economy gives rise are non-explosive, in the sense that the adjustment process converges to equilibrium or to a cycle of order two, in which market prices 'gravitate' around equilibrium prices.
However, in addition to the assumptions criticized above from the Nikaido and Duménil and Lévy models that the Benetti et al. model reproduces, it has the following two additional problems:
First, the balance settlement rule that they assign, as well as being unrealistic and naïve, is very restrictive in two different senses: 1) its feasibility can only be guaranteed when the property described in footnote 8 is met, meaning that this condition is quite strong for a market society (because, due to the social division of labor, one would expect that in these societies inter-industrial dependence would be significantly higher than intra-industrial dependence), and 2) the balance settlement rule can only be used when the model is set in a bisector economy, since in an economy with n sectors, with n > 2, there may be compatibility problems between the accumulation plans of capitalists with positive monetary balances and the availability of commodities produced by capitalists with monetary deficits.
A second problem is that the Cantillon rule is a very particular market mechanism that is not used in any actual market (as other market mechanisms such as the double auction or the first price sealed-bid auction are used); and there is no evidence to suggest that the same stability results could be obtained using these alternative market mechanisms, or individual pricing rules under imperfect competition.
Thus, this section can be concluded by stating that none of the classical-Marxian monetary models of the theory of value reviewed here are completely satisfactory, due to the specificness of their hypotheses that make their results very limited in scope.
CONCLUSIONS
A coherent theory of value must be monetary and must analyze in a disaggregated manner the dynamics of the economy, considering the monetary and real interdependence relations that exist between all individual economic activities. For this reason, the real and the strictly monetary approaches cannot be considered coherent approaches to the theory of value. The former cannot explain decentralized price and exchange formation based on an economy without money, and the latter cannot explain how prices solve the coordination problem posed by extra-monetary interdependence relations (such as technical-productive relations between commodities that must be fulfilled to guarantee their production).
In this paper, we reviewed the main models proposed within the framework of a monetary approach to the theory of value. We have shown that the models of Patinkin, Arrow et al., and Nikaido require centralized instances that make them incompatible with market societies, and so should be rejected. In contrast, the models of Fisher, Duménil and Lévy, and Benetti et al. explain how prices work consistently within market societies. However, these models are not free of problems. In the case of Fisher's model, its main problem is that its conditions are so general that nothing can be said about the adjustment process and the resulting equilibrium state other than its existence and stability properties. On the other hand, in the case of the Duménil and Lévy and the Benetti et al. models, these are based on such specific hypotheses that their results have a very limited scope, circumscribed to the fulfillment of such hypotheses.
For this reason, it can be said that the theory of value currently faces a dilemma between the degree of generality of its results and the specificity of its content. It seems that the more general the hypotheses used in the models (which allows their results to have a much wider scope), the less informative they are, in the sense that not much can be said about the characteristics or properties other than the stability of the economies (for example: whether or not they have quantity constraints, whether they are optimal or not, whether they are perfectly competitive or not, etc.). And vice versa, the more specific the results are, the less generalizability they have, in the sense that they depend on very particular hypotheses such as a two-sector economy, with linear technology, specific rules for price determination, exogenous accumulation rates, etc.
In a future research agenda, we see the need to analyze the relations between the generality of the results obtained by Fisher's model with the particularity of the results obtained from models such as those of Duménil and Lévy and Benetti et al. (or eventually others), either by formulating particular models in the neoclassical framework that can be compared with Fisher's general model or by generalizing the classical-Marxian monetary and disequilibrium models such as those of Duménil and Lévy and Benetti et al., so that the general stability conditions that these models have shown under their particular hypotheses can be established in different conditions. Regardless of whether a neoclassical or classical-Marxian theoretical framework is applied, the monetary approach to the theory of value must follow this research path if it is to achieve preeminence as the theoretical core of the science of market societies.