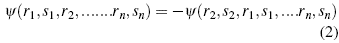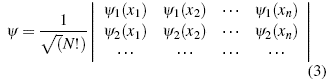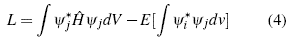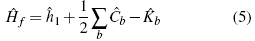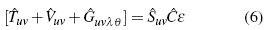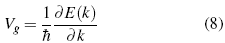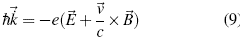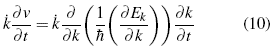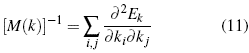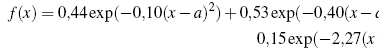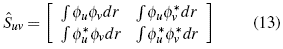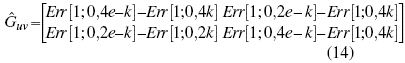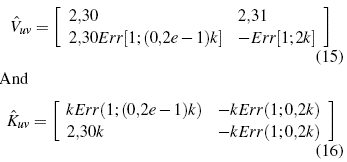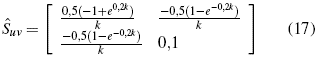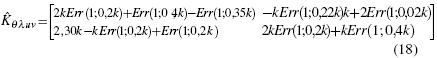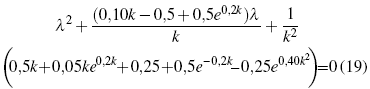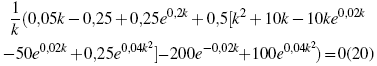1. INTRODUCCIÓN
The problems that fall under the quantum regime have great implication and application in many technological areas; this is quite clear in the light of the fact that most of the technological evolution is closely linked to the ever-greater understanding of quantum mechanics. Because of this, the dynamic of an electron, in an infinite periodic and crystalline lattice is of great interest from the quantum perspective, due to that the dynamic of this electron exhibits an interesting behaviour that can contribute to greater advances in different areas of technology. The problem will be solved by using self-consistent Hartree-Fock-Roothaan method [1]-[6], which is a powerful tool for solving complex problems. Prior to this, we will give an introduction to the HFR and Bloch theories, which gives account of dynamic of this electron.
2. MÉTODOS
2.1. Hartree-Fock Theory and Roothaan equation
The solution to problems in quantum mechanics, in the non-relativistic and stationary regime, is based on the solution to the time independent Schrödinger equation, which is responsible for establishing all of the properties of the system 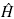 ψ = E ψ, where
ψ = E ψ, where 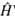 is the Hamiltonian operator, which establishes all of the interactions of the system, ψ is the normalized wave function, and E is the eigenvalue of the energy, which is acquired as a consequence of the measurement of the Hamilton operator in the system [1]-[3]. Although this equation takes different forms, according to the studied system, with the increase in the complexity of this system, it becomes increasingly complex, reaching the point where its solution does not possess an analytical form, and with this, it is more viable not to directly use the equation for its solution, but to apply the variational principle to the solution of the problems. This establishes that the expected value of the Hamilton operator, has as its eigenvalue, the energy in the base state, and its variation is carried out to find those energy values that minimize the integral of action [6]-[8].
is the Hamiltonian operator, which establishes all of the interactions of the system, ψ is the normalized wave function, and E is the eigenvalue of the energy, which is acquired as a consequence of the measurement of the Hamilton operator in the system [1]-[3]. Although this equation takes different forms, according to the studied system, with the increase in the complexity of this system, it becomes increasingly complex, reaching the point where its solution does not possess an analytical form, and with this, it is more viable not to directly use the equation for its solution, but to apply the variational principle to the solution of the problems. This establishes that the expected value of the Hamilton operator, has as its eigenvalue, the energy in the base state, and its variation is carried out to find those energy values that minimize the integral of action [6]-[8].
This principle is essentially a little more versatile for find such values, but the function that describes the system must meet certain conditions, which are imposed by the principle of anti-symmetry, a consequence of the indistinguishability of particles, which states that permutation or change of a pair of particles alters the position and spin function of the system, changing their direction, so changing the two particles alters the sign of the function [9]-[10].
r n denotes the part of the wave function that establishes the position and the dependent part of the spin s n, so the form of the function that correctly describes the system is correctly established. The generalization of this principle to n particles is established by means of the Slater Determinant.
Additionally the wave function, must be complete, i.e. it must be the sum of an infinite set of wave functions independent of each other,. In practice, this set is not infinite, but is truncated at a particular term [8]. This can be better visualized when establishing the solution to the specific problem ψ = Σ ί C ί φ ί . Where the coefficients C i are found by minimizing the energy and orthonormality of the wave functions. In order to deduce the Hartree-Fock operator, which transforms the many-body problem into many single-body problems, we use the nuclear Lagrangian, which is a consequence of the Schödinger equation, the normalization of the function.
The respective variation of the Hartree-Fock operator δL = 0, leads to Hartree-Fock eigenvalues:
and the form of the eigenvalues equation 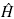 ƒ
ψ = E ψ. In this expression ίι
1, revers to the sum of the expected value for the kinetic and potential energy of the system [11], Ĉ
b is the so-called Coulomb operator, which refers to the interaction between the particles, and
ƒ
ψ = E ψ. In this expression ίι
1, revers to the sum of the expected value for the kinetic and potential energy of the system [11], Ĉ
b is the so-called Coulomb operator, which refers to the interaction between the particles, and 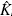 b
is the exchange operator. This operator has no analogy in any other branch of physics, so it is only established from the operational part and the constant is the result of the normalization of the function, in this particular case, to be carried out for n = 2. However, the solution of the Hartree-Fock equation is quite complex, since it is an integrated differential equation. Nevertheless, there is a great value simplification, which transforms a problem of this type into an entirely matrix problem, the latter being simpler to solve. In order to this simplification to occur, one must equal the normalization condition in the Hartree-Fock equation, it is organized, and the following matrix equation results:
b
is the exchange operator. This operator has no analogy in any other branch of physics, so it is only established from the operational part and the constant is the result of the normalization of the function, in this particular case, to be carried out for n = 2. However, the solution of the Hartree-Fock equation is quite complex, since it is an integrated differential equation. Nevertheless, there is a great value simplification, which transforms a problem of this type into an entirely matrix problem, the latter being simpler to solve. In order to this simplification to occur, one must equal the normalization condition in the Hartree-Fock equation, it is organized, and the following matrix equation results:
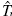 uv represents the matrix of the kinetic energy associated with the system [12],
uv represents the matrix of the kinetic energy associated with the system [12], 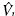 uv
the matrix associated with the potential that the system experiences, Ĝ
uv
xg is the matrix of exchange, which alludes to the form of interaction in the system, and Ŝ
uv
[
12]-[13] is the matrix called metrica, responsible for normalizing the Fock operator.
uv
the matrix associated with the potential that the system experiences, Ĝ
uv
xg is the matrix of exchange, which alludes to the form of interaction in the system, and Ŝ
uv
[
12]-[13] is the matrix called metrica, responsible for normalizing the Fock operator.
2.2. Bloch's Theory
The dynamic behavior of electrons in different media is established by Bloch's theory, or the semi-classical model. This is based on the fact that an electron will not possess a velocity comparable to that of light in crystalline media [13-15]. These crystalline media are defined as periodic structures, known as the Bravaris lattice. Therefore, this theory has as its structure the deBroglie equations, which describe the electron and its undulatory properties E = hƒ =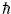 ω and
ω and 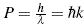 , E, represents the energy, h is the Planck constant, ƒ the linear frequency, ω the angular frequency, and λ the the wavelength, and k the wave vector.
, E, represents the energy, h is the Planck constant, ƒ the linear frequency, ω the angular frequency, and λ the the wavelength, and k the wave vector.
Another of the results of wave theory, group velocity, is used which describes the behavior of the electrons, which are denoted as Bloch electrons [1]-[2].
And the velocity in terms of deBroglie?s equations[16]:
With this, the behavior that is established as semi-classical, has several restrictions. One of them is that the electrons can not make jumps between bands, that is to say that they are confined by some potential. The next condition is that they must possess a form specifies in their equations of motion, and their behavior must be determined by them in a biunivocal form, as long as they do not violate Heisenberg/s principle of indeterminacy which, is achieved by not giving a direct specification of the position of that particle exactly in the region of Bravaris [17-19]. Therefore, the equation of motion (force 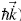 ) that describe the behavior of the electron with charge and velocity (e,
) that describe the behavior of the electron with charge and velocity (e, 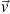 ) under interaction with magnetic (
) under interaction with magnetic (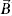 ) and electric (
) and electric (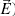 ) fields in the crystal lattice in the Gaussian units system is[20]:
) fields in the crystal lattice in the Gaussian units system is[20]:
As the last result adopted from Bloch's theory [10] for the dynamic of the electron, the projection of the change of λ is required, with its acceleration, since both are in the same direction but in opposite directions, that is to say the potentials make a change in the speed of these electrons in the network, in some sections of the infinite structure accelerating it and in others slowing it down, thereby establishing that the movement of this electron is like that of a free particle[21].
Reorganizing the expression, to refer to each of the components, of the different wave numbers and summing up all possible values of this factor, the effective mass tensor is established [13]-[14].
The important context of this equation is that although the explanation of the dynamic behavior of the electron in Bloch/s theory is complex [15]-[16], a simplification can be made by explaining the electron as a quasi-free particle, in the lapse of time of the interactions a different mass. This is the simplification carried out from the perspective of the effective mass, in essence, this quantity is a tensor; however, for the specific problem, it is reduced to a constant[22].
3. Results and Discussion
3.1. HFR method applied to finding the effective mass
From the two perspectives that have been established for our particular problem, which are the dynamic behavior of an electron in an infinite and periodic crystalline conformation, and many-body quantum mechanics, we want to solve the dynamic behavior of this electron but using the HFR theory [17]-[18]. We will start with the way to establish the initial function, emphasizing that if the crystalline conformation possesses free loads and they are induced an electric field, these charges will be realigned with this field, in such a way that the net electric field will be zero internally, a simplification that will help in the same way as the solution type HFR. There- fore, in HFR theory, an initial or start function must be established, but not just any function adequately approximates the problem. Thus a specific amount is chosen, which must be maximized or minimized, depending on the case being searched for. This is the metric matrix arranged 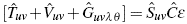 . The most-used types of functions are the Slater Type Orbital (STO) (exp-r) and the Gauss form (lsG) (exp-r2) or the superposition of both. For this, it is repeated a number of times for certain determined values[23-25]. This variable, is included just as an adjustment value, since the HFR method is approximate.
. The most-used types of functions are the Slater Type Orbital (STO) (exp-r) and the Gauss form (lsG) (exp-r2) or the superposition of both. For this, it is repeated a number of times for certain determined values[23-25]. This variable, is included just as an adjustment value, since the HFR method is approximate.
The carrying out of the corresponding calculations for the matrix of metric integrals and potential energy matrix, that were established from the initial functions, leads to the following results. In figure 1, the initial function used for the self-consistent calculation is shown, the values of α are chosen in such a way as to minimize this function. Under the considerations of the variational principle in quantum mechanics, by guaranteeing the minimum initial function (in this case with STO (3G) or STO) the probability G density will also be[26].
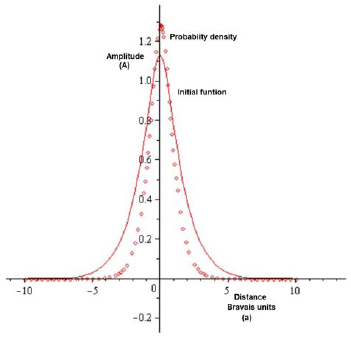
Figure 1 Initial function used for the treatment of the specific problem (continuous), and probability density (diamonds)
Table 1 From this it can be seen that the optimum value is between 4,0 and 5,0, after which the value of the integral falls abruptly, so by choosing the first exponent of the initial function, after performing this process three times to find the respective exponents, the startup function (type STO-3G, by the three coefficients found) is established. Here the variable is inserted as x, only by note, but this distance in essence is radial to the position of periodicity and α is the unit cell length of Bravaris lattice. The ? values are varied in the numerical metric integration S? to minimize its valuel and thus, guarantee a self-consistent result from the variational point of view. The α-values are varied in the numerical metric integration S to minimize its valuel and thus, guarantee a self-consistent result from the variational point of view.
| value | α | value | α |
| 1.33 | 0.1 | 5.95 | 2.0 |
| 1.88 | 0.2 | 7.29 | 3.0 |
| 2.66 | 0.3 | 8.42 | 4.0 |
| 2.99 | 0.5 | 9.41 | 5.0 |
| 4.22 | 1.0 | 1,0 χ 10-7 | 6.0 |
Obtaining:
Where Err(i;k), represents the function error, evaluated in the parameters (i, j). Establishing a similar process for the kinetic and potential energy matrix.
With the initial function established, we proceed to find the metric matrix, which for simplicity has been established a 2 χ 2. Each term of this matrix comprises an integral in a given range, which is determined by the Bravais parameter, assigning, a mathematical package that is used for the realization of this specific calculation[27].
Throwing for these integrals between 0 and 10nm (Bravais value)[28]. For the calculation of the effective mass, a functional form of all the parameters referring to k is necessary, so in the initial function a direct reference will be made to this parameter, leaving:
which are the respective values for the kinetic energy matrix and the potential energy matrix, which is operated together to obtain the Fock operator obtaining the following expression:.
The next step for the solution of the Fock operator, can be approached from two different perspectives, which differ only in their operative form[29], but in essence the value found is the same. Therefore, the operator’s solution is chosen by executing its characteristic polynomial, for which one must choose one of the appropriate solutions[30]. Since the matrix of this operator is 2x2, the polynomial will have the same order as the dimensions of the matrix, which is executed in the mathematical package, arriving at the following expression:
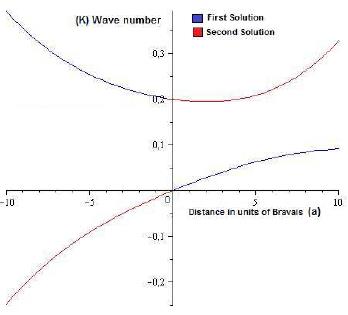
This is only one of two solutions, they differ only in some signs and some constants, but to get a better visualization of the respective behavior of these solutions as a function of k, they have been plotted, in order to more clearly establish the reason for the choice of some of them.
In Figure 2, we can observe the behavior of both solutions, one of which is always maintained in the positive range for the values of the Fock operator, while the other solution has negative values for its value, which is inadmissible from the mathematical perspective, since this indicates that the electronic integrals and the exchange integrals do not converge to positive values, and from the physical point of view the negative value of the mass is discarded. Since these are the eigenvalues for the Fock operator, which are the energy eigenvalues, which are given as a function of the wave number k. However, what is desired is not the energy values, but the terms of the mass that are related in function to the energy, according to expression [10] or which twice the expression that was found as a solution for the Fock operator with respect to the wave number is derived, and evaluating it, not in zero, but in a value so close to Zero as desired, since the use of an approximation function requires that its evaluation not be established at a particular point, but rather as close as desired to the point of evaluation, obviously with some restrictions, such as It is the value of Bravais, with this same procedure is the value of the effective mass for the particular problem. However, since the objective is to illustrate the problem in a more complete form, the same algorithm has been carried out with different functions, and they are listed in the following table, making reference to the accuracy of each of the functions used and the value obtained for the effective mass, in which the degree accuracy is compared with the experimental value found. The approximation quality of the functions used by the HFR method can be clearly seen, and as this method establishes solutions to problems that apparently do not agree with its area of application[20-23]. It should be clarified that STO-3G and STO-2G, refers to the initial function used, where the first is an overlap of a Gauss-like function composed of two terms and the next composed of three terms[25-27].
4. CONCLUSIONES Y RECOMENDACIONES
The study of quantum mechanics and its respective generalization to many bodies, in most cases is approached in the form of its historical or conceptual development, that is to say, from the analytical perspective, whereby the SCF development is seldom structured in the foregoing form, giving special emphasis to its operational form and its respective application to a particular problem. SCF methods are seldom treated in scientific problems solutions, in articles and specialized texts, but without emphasizing the way of proceeding and operating method.