Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
Tecné, Episteme y Didaxis: TED
versão impressa ISSN 0121-3814
Rev. Fac. Cienc. Tecnol. no.32 Bogotá jul./dez. 2012
La historia como recurso didáctico: el caso de los Elementos de Euclides*
History as a didactic resource: the case of Elements by Euclids
Clara Helena Sánchez B**
*Este trabajo está basado en el cursillo realizado el XX Encuentro de Geometría y sus Aplicaciones realizado en la Universidad Pedagógica Nacional, 23 al 25 de junio de 2011.
**Docente Universidad Nacional de Colombia. Bogotá, Colombia. chsanchezb@unal.edu.co
Recibido: 15/01/12, y aprobado: 15/11/12
Resumen
Con la introducción de la matemática moderna en la enseñanza básica y media en la segunda mitad del siglo XX se descuidó seriamente la enseñanza de la geometría para privilegiar el álgebra y la teoría de conjuntos. Este descuido ha traído graves consecuencias en la formación matemática de nuestros estudiantes, razón por la cual se está revaluando seriamente el papel de la geometría en la formación de nuestros niños y jóvenes. Son numerosos los artículos que se encuentran en la red en los cuales se analiza este hecho y se hacen propuestas de qué y cómo enseñar geometría en la enseñanza básica y media. Entre los recursos didácticos que se consideran hoy en día para el mejoramiento de la enseñanza de las matemáticas en todos los niveles de formación se encuentra la historia de la disciplina, pues ella nos per-mite apreciar el origen de los conceptos matemáticos y las vicisitudes que han tenido a través del tiempo para consolidarse como hoy los conocemos. En particular, se resalta la importancia de la obra Elementos de Euclides, en la cual se pueden encontrar herramientas didácticas para la enseñanza y aprendizaje de la geometría, el álgebra y la teoría de números. En este artículo se presentan algunos aspectos de esta obra que pueden ser útiles en la enseñanza de la geometría.
Palabras Clave Historia de las matemáticas, geometría, Elementos de Euclides, didáctica de las matemáticas.
Abstract
In mid- 20th century the introduction of modern Mathematics in primary and high-school curricula privileged Algebra and set theory over Geometry. This oversight has created deep consequences in the mathematical formation of our students. Nowadays this situation has seriously led to study the role Geometry plays in the education of our children and young people. Thus, many proposals have been offered to solve the problem of how to teach geometry at these levels. One of the proposals offered is the use of the history of mathematics to improve the teaching mathematics, since its history allows valuing and understanding of the origin of mathematical concepts and the vicissitudes they had undergone up to the consolidated form we know them today. In particular, I highlight the importance of the Opus Dei of Elements by Euclid, which we can find didactical tools to learn geometry, algebra and number theory. In this paper I present some tools about Elements useful for teaching and learning of geometry.
Keywords History of Mathematics, Geometry, Elements by Euclid, didactic of Mathematics.
Introducción
Con la introducción de la matemática moderna en la enseñanza básica y media en la segunda mitad del siglo XX se descuidó seriamente la enseñanza de la geometría para privilegiar el álgebra y la teoría de conjuntos1. Este descuido ha traído graves consecuencias en la formación matemática de nuestros estudiantes y, por esta razón, se está revaluando seriamente el papel de la geometría en la formación de nuestros niños y jóvenes. Son numerosos los artículos que se encuentran en la red en los cuales se analiza este hecho y se hacen propuestas de qué y cómo enseñar geometría en la enseñanza básica y media2.
En docentes de educación escolar se percibe un desconocimiento casi total de la historia de la geometría y particularmente del papel que ha tenido la obra Elementos, de Euclides, tanto en el desarrollo de la matemática como en otras ramas del conocimiento de gran impacto en la cultura occidental. En Elementos hay componentes didácticos para la geometría, el álgebra y la teoría de números; además, durante muchos siglos fue el gran paradigma para aprender a razonar correctamente. Un recorrido por esta obra, sus antecedentes, su contenido, su estructura, y el impacto causado ya sea por sus fortalezas o sus limitaciones, es un recorrido por la historia de la geometría y, como tal, un recurso didáctico valioso para ser tenido en cuenta en la enseñanza de las matemáticas.
Antes de continuar, se proponen algunas preguntas que el lector deberá responder con el propósito de orientar el contenido del presente artículo.
Sobre los Elementos de Euclides
¿De qué época es la obra? ¿Dónde fue escrita? ¿Para qué fue escrita? ¿Qué contiene? ¿Qué áreas de la matemática aborda? ¿Cómo está estructurada? ¿Por qué es tan importante en la historia de la matemática? ¿Por qué es tan importante en la historia de la cultura occidental? ¿Qué limitaciones tiene?
Sobre Euclides de Alejandría
¿Dónde y cuándo nació? ¿Fuera de los Elementos escribió algo más? ¿Qué tan original es Euclides en su obra los Elementos? ¿Cuál es el quinto postulado de Euclides? ¿Cuál es el gran aporte de Euclides a la matemática?
Sobre la enseñanza de la geometría
¿A qué se llama matemática moderna? ¿Por qué la enseñanza de la geometría se afectó por la enseñanza de la matemática moderna? ¿Qué se pretendía con la enseñanza de la geometría clásica? ¿Qué se pretende ahora con la enseñanza de la geometría?
Abordaremos cada una de esas preguntas y mostraremos que la obra de Euclides de alguna manera sigue vigente y que la historia de la geometría y la de su enseñanza está marcada por dicha obra trascendental de la historia de la humanidad.
Es prudente resaltar que, desde sus comienzos, la matemática ha tenido dos aspectos: a) prácticos, los que se refieren a la solución de problemas que le presenta el mundo exterior relacionados con contar, medir, pesar, trazar linderos, calcular impuestos, etcétera. Éstos requieren con frecuencia métodos empíricos, algoritmos, para solucionarlos. b) Teóricos, en los que una élite social, los nobles en la Antigüedad, se dedicaban a pensar en los conceptos abstractos de las matemáticas. Estos personajes no estaban interesados en la matemática práctica y dejaron en sus escritos sus aportes a la disciplina. Por el contrario, los matemáticos prácticos dejaron muy poco testimonio escrito, y, en consecuencia, es casi imposible saber cómo lograban resolver sus problemas. En la historia de la geometría encontramos claramente los dos aspectos mencionados.
Los orígenes de la geometría
Según el historiador Heródoto (484-425 a.C.) la geometría nace en Egipto debido a la necesidad de trazar los linderos de las tierras cada vez que el río Nilo las inundaba, pues a partir de esos linderos había que pagar los impuestos. Del trabajo de esos agrimensores quedan algunas recetas, métodos prácticos, para calcular longitudes, áreas y volúmenes que se encuentran en los Papiros de Ahmes y de Moscú. A los geómetras se les llamaba tensadores de cuerdas porque con cuerdas y estacas se hicieron construcciones y se reconstruyeron las fronteras de los terrenos alteradas por los desbordamientos del Nilo. Los tensadores de cuerdas podían construir ángulos rectos dividiendo una cuerda en 3, 4 y 5 partes de tal manera que formaran un triángulo rectángulo. Las impresionantes construcciones de los egipcios llevan a concluir que tenían conocimientos de geometría práctica sorprendentes.
Autores como Aristóteles (384-322 a.C.) y recientemente Seidenberg (1952), consideran que la geometría tiene un origen ritual. El primero sostenía que el ocio de la clase sacerdotal había desarrollado la geometría para construir templos y altares. El segundo encuentra en los Sulvasustras3, trabajos de los hindúes sobre construcción de altares, una fuente valiosa para sustentar su posición. Los altares, en los cuales se hacían sacrificios para los dioses, tenían diferentes formas, circulares, cuadrados, y cualesquiera otras dependiendo del ritual. Seidenberg brinda el ejemplo de un altar en forma de halcón compuesto de rectángulos, para el cual se usó el teorema de Pitágoras. Por otro lado, es bastante conocida la historia sobre el oráculo de Delfos, relacionada con el problema de la duplicación del cubo. El dios Apolo solicitaba que su altar en forma de cubo fuera duplicado, al ser doblado cada lado se obtuvo un altar ocho veces mayor con lo cual no se cumplieron las exigencias del dios. Los intentos por resolver el problema dieron lugar a interesantes soluciones geométricas, con instrumentos distintos a la regla y el compás euclidianos. Se destaca la de Hipócrates de Quios, que reduce el problema a encontrar dos medias proporcionales entre V y 2V, siendo V el volumen del cubo considerado. Esto es, hallar x y y tales que V:x::x:y:: y:2V, lo cual conduce a encontrar el punto de intersección entre dos parábolas o una parábola y una hipérbola como puede constatar el lector4.
Otros autores como Paulus Gerdes (2001) o Morris Kline (1959) destacan el hecho de que vivimos en un mundo lleno de objetos que tienen formas y tamaños. La luna, y el sol son objetos circulares y esféricos, las hojas de las plantas, las flores, nos muestran formas particulares, las celdas de una colmena de abejas o las telarañas son construcciones extraordinarias de la naturaleza para "apropiarse" del espacio de la mejor manera. Los caracoles tienen formas espirales; el horizonte es una línea recta. Basta pues observar el mundo que nos rodea para encontrar formas geométricas; el hombre tiene la capacidad de abstraer de esas formas de objetos concretos entes ideales que se convierten en objeto de estudio de la geometría.
Kline (1959) se preguntaba cómo los creadores de la geometría pensaron acerca de líneas perpendiculares, líneas paralelas, figuras similares o congruentes y cuestiones de este tipo; responde diciendo que "todas estas relaciones se hallan observando la naturaleza. Los árboles crecen perpendiculares al suelo, las riveras de un río pueden considerarse paralelas. Sin embargo el paso de lo concreto a lo abstracto debió darse en muchos años de evolución de la especie humana"(pp. 73-75). En las civilizaciones egipcia y babilonia hay un testimonio de este paso, lo cual justifica la historia tradicional de los orígenes de la geometría con los cuales comenzamos esta sección.
Geometría práctica y geometría especulativa
Los conocimientos, prácticos y concretos, que tenían los egipcios y babilonios sobre geometría pasaron a la cultura griega a través de Tales de Mileto y los pitagóricos. Los griegos de la época dorada, siglos VI a III a.C., quienes concibieron las matemáticas abstractas y deductivas estuvieron especialmente atraídos por las formas y los movimientos que observaban en los cielos; geometría y astronomía estaban íntimamente relacionadas. En el Quadrivium medieval la astronomía era la aplicación práctica de la geometría, como la música lo era de la aritmética para la escuela pitagórica.
El desarrollo de la geometría como disciplina tiene un punto culminante con los Elementos de Euclides, obra en la cual encontramos lo que en textos antiguos denominaban geometría especulativa, para distinguirla de la geometría práctica usada por los agrimensores o los ingenieros en sus prácticas profesionales5.
La enseñanza de la geometría
Nadie entra aquí si no sabe geometría.
Letrero a la entrada de la Academia de Platón
Dos anécdotas se cuentan en la historia de las matemáticas sobre la enseñanza de la geometría. La primera se refiere a que Menecmo, ante una pregunta de Alejandro Magno, le dijo que no había un camino especial de aprendizaje de la geometría para los reyes. La misma historia tiene como protagonistas a Euclides y Tolemeo. La otra anécdota se refiere a que algún alumno preguntó a Euclides sobre qué ganaba él con lo que le estaban enseñando, a lo que Euclides respondió: "Denle tres monedas a este alumno para que gane algo con lo que aprende". Las dos historias merecen reflexión; el que en geometría no haya camino especial para los reyes significa que todos podemos acceder a su estudio pero requiere esfuerzo; la segunda, que el conocimiento es valioso en sí mismo y no hay que buscarle una recompensa monetaria. Sin embargo, los que enseñamos o hacemos matemática constantemente tenemos que enfrentarnos a esa pregunta y debemos tener una respuesta distinta de la dada por Euclides para motivar a nuestros estudiantes.
Las preguntas sobre qué, cómo y para qué enseñar matemáticas, tienen mucho sentido y, por tanto, no podemos pasarlas por alto. Una cosa es la geometría del que se va a dedicar a las matemáticas y otra diferente la geometría que debe conocer todo el mundo. Desde los años 1970, cuando se vio rápidamente el fracaso de la enseñanza de la matemática moderna en los colegios, se viene intentando reposicionar la enseñanza de la geometría. Veamos:
La enseñanza de la geometría es una de las áreas de las matemáticas en las que hay más puntos de desencuentro entre matemáticos y educadores, no solo en relación con sus propósitos y contenidos sino también con la manera de enseñarla. Es probable que esto ocurra debido a los aspectos que abarca: por un lado la geometría es considerada como una herramienta para el entendimiento, tal vez la parte de las matemáticas más intuitiva, concreta y ligada a la realidad. Por otra parte, la geometría como disciplina se apoya en un proceso extenso de formalización, el cual se ha venido desarrollando por más de dos mil años en niveles crecientes de rigor, abstracción y generalidad (Schulmaister, 2008).
De hecho, por más de dos milenios, el texto Elementos de Euclides sirvió de guía para la enseñanza de la geometría prácticamente en todas las culturas que la conocieron. En Colombia, la traducción de la versión de Legendre (1866) fue el texto obligatorio en el siglo XIX y muchos estudiamos en el siglo XX con el texto de Bruño (s.f.; 1921), en sus diferentes ediciones, ambos adaptaciones escolares de los Elementos6.
Geometría como ciencia demostrativa
Los historiadores, por lo general, consideran a Tales de Mileto (siglo VI a.C.) como el primer matemático que demostró teoremas. Se cuenta que Tales midió la altura de las pirámides de Egipto teniendo en cuenta la longitud de las sombras en el momento en que estas, proyectadas por un palo vertical, eran iguales a sus alturas. Con ello estaba aplicando propiedades de los triángulos semejantes. A él se adjudican los siguientes teoremas de la geometría:
- Todo ángulo inscrito en una semicircunferencia es recto.
- Todo círculo queda dividido en dos partes iguales por su diámetro.
- Los ángulos de la base en un triángulo isósceles son iguales.
- Los ángulos opuestos por el vértice en dos rectas que se cortan son iguales.
- El teorema de congruencia de triángulos: ángulo, lado, ángulo.
No se sabe cómo hizo Tales las demostraciones, pero suponemos que usó un método empírico ya que todos ellos pueden ser aceptados fácilmente de manera intuitivao por observación directa.
El primer matemático al que se le reconoce una demostración, con el sentido que esta tiene en la actualidad, es Pitágoras o mejor la escuela pitagórica, al demostrar la inconmensurabilidad de la diagonal de un cuadrado con respecto a su lado por medio del método de reducción al absurdo. La posible demostración original, en términos geométricos, puede encontrarse en Vega (1990), la cual dio origen a los números irracionales, así en la época fueran rechazados como tales.
La demostración usual que hoy conocemos de "√2 es un número irracional" sigue el mismo tipo de razonamiento de los pitagóricos, pero traducido al lenguaje algebraico. Este descubrimiento ocasionó una "ruptura" entre aritmética y geometría, pues los pitagóricos consideraban que todo era número o relaciones entre números, entendiendo por número a los naturales mayores que dos, y la existencia de magnitudes a las cuales no se les podía asignar una razón numérica contradecía sus creencias. Este hallazgo hizo que la geometría se privilegiara sobre la aritmética y con ello en Grecia la geometría adquirió el estatus de ciencia por excelencia, por el rigor con que se hacían las demostraciones.
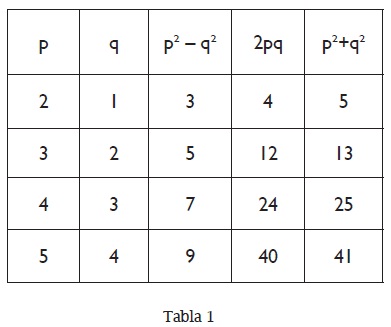
Igualmente, a los pitagóricos se debe la primera demostración del teorema de Pitágoras. Difícilmente una persona medianamente educada no ha oído hablar de este teorema, pero, ¿cuál es su historia? Los babilonios dejaron registradas en sus tablillas unas cuantas triplas pitagóricas, esto es, triplas de números enteros positivos (a, b, c) que cumplen la condición a² + b² = c². Pero el trabajo fue más de tipo algebraico que geométrico. En particular encontraron que dados dos números naturales cualesquiera, p y q, se podían formar triplas pitagóricas con los números p² - q², 2pq y p²+ q². Algunos casos los presentamos en el siguiente cuadro considerando a p y q números naturales y p mayor que q.
La pregunta que inmediatamente surge es si esas son las únicas posibilidades para poder establecer una generalización. El teorema de Pitágoras,"en un triángulo rectángulo el cuadrado sobre la hipotenusa es igual a la suma de los cuadrados sobre los catetos"7 establece esa generalización pero de manera geométrica: cuando a y b son las longitudes de los catetos y c es la hipotenusa de un triángulo rectángulo la ecuación a² + b² = c² vale. Pero, en este caso a, b, c muy posiblemente no son simultáneamente números enteros positivos.
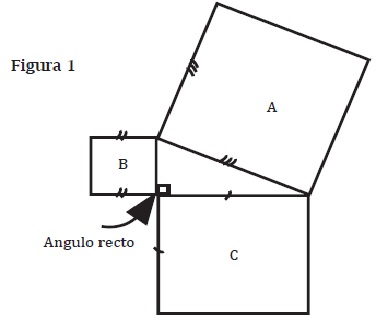
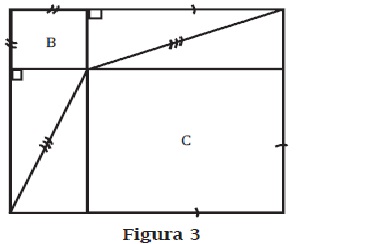
La demostración que presentamos a continuación, se supone es la original de Pitágoras, que aunque no tan rigurosa como la de Euclides merece estudiarse, precisamente por ser intuitivamente bastante clara y accesible a niños y jóvenes que apenas empiezan a formarse en lo que es una demostración matemática. En la figura 1 vemos un triángulo rectángulo sobre cuyos lados se han construido los respectivos cuadrados. Se trata de probar que el área del cuadrado A es igual a la suma de las áreas de los cuadrados B y C.
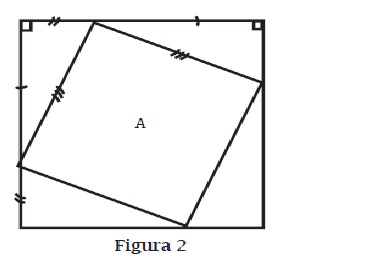
En la figura 2 vemos cuatro triángulos iguales al original y un cuadrado al centro, el formado por la hipotenusa. En la figura 3 vemos nuevamente los cuatro triángulos y dos cuadrados menores, los formados por los catetos. Ahora bien "si a cosas iguales le restamos cosas iguales, obtenemos cosas iguales". Y así, al restar los cuatro triángulos en los dos cuadrados, resulta que el cuadrado sobre la hipotenusa A es igual a (la suma de) los cuadrados sobre los catetos B y C. Esto es, las áreas que quedan son iguales. Obsérvese, sin embargo, que en ningún momento se mencionaron, y mucho me-nos se necesitó conocer, las longitudes de los lados para demostrar el teorema.
Creemos que la anterior es una excelente demostración del teorema para niveles muy elementales de matemática o para un trabajo de divulgación. En otras palabras es un buen argumento, teniendo en cuenta el tipo de público al cual estaría dirigido. Es un mal argumento para un público calificado de matemáticos, pues no es una demostración rigurosa del teorema8, esta requeriría presentar un sistema axiomático como el de Euclides que presentaremos más adelante. Podemos igualmente proceder de acuerdo con las leyes de la lógica como lo hace el libro de Moise (1963), muy popular entre nosotros, en el capítulo 13 titulado "Regiones poligonales y sus áreas".
Los Elementos de Euclides
La obra cumbre de la matemática griega la encontramos en Elementos de Euclides9; es sin duda la obra matemática más famosa de todos los tiempos. Con la Biblia y el Quijote tienen el récord de ser las obras más ampliamente usadas, estudiadas, y con más ediciones en todo el mundo. Fue escrita hacia 300 a.C, como un libro de texto para enseñar matemáticas en el Museo de Alejandría. Elementos ejerció una enorme influencia en el pensamiento científico y sirvió como texto de enseñanza de la geometría por más de 2000 años, como ya anotamos. Su importancia radica, no solo en la matemática que allí se encuentra sino en su estilo de razonamiento, el que se conoce como razonamiento al estilo geométrico. Este ha sido tomado como modelo ideal en otras ramas de la matemática y en otros campos del saber como la filosofía o la física. El valor de la obra radica fundamentalmente en la recopilación y sistematización que Euclides de Alejandría10 hizo de gran parte de la matemática de su época; es lo que se conoce con el nombre de método axiomático. A partir de unas cuantas definiciones, unos postulados y nociones comunes (o axiomas) se demuestran las proposiciones de la teoría.
La obra está compuesta de 13 libros sobre temas de geometría, aritmética y álgebra; contiene 467 teoremas sobre geometría plana (libros I a IV), teoría de la proporción (libros V a VI), teoría de números (libros VII a X) y geometría del espacio (libros XI a XIII). Cada libro tiene definiciones y teoremas salvo el primero que contiene además 5 postulados y 5 nociones comunes o axiomas. Los axiomas son elegidos como verdades evidentes en sí mismas y comunes a todas las ciencias. Los postulados son escogidos como verdades evidentes en sí mismas específicas de una ciencia en particular, en este caso la geometría.
Las nociones comunes
- Las cosas iguales a una misma cosa son también iguales entre sí.
- Y si se añaden cosas iguales a cosas iguales, los totales son iguales.
- Y si de dos cosas iguales se quitan cosas iguales, los restos son iguales.
- Y las cosas que coinciden entre sí son iguales entre sí.
- Y el todo es mayor que la parte.
Los postulados
- Postúlese el trazar una línea recta desde un punto cualquiera hasta un punto cualquiera.
- Y el prolongar continuamente una recta finita en línea recta.
- Y el describir un círculo con cualquier centro y distancia.
- Y el ser todos los ángulos rectos iguales entre sí.
- Y que si una recta al incidir sobre dos rectas hace ángulos internos del mismo lado menores que dos rectos, las dos rectas prolongadas indefinidamente se encontrarán en el lado en el que están los [ángulos] menores que dos rectos.
Los tres primeros postulados se conocen como herramientas euclidianas, ya que permiten las construcciones geométricas. El primero y segundo permiten trazar rectas, y el tercero trazar círculos; por eso se dice que en Elementos encontramos construcciones con regla y compás. Pero, una regla sin marcas y un compás que se cierra al levantar las puntas del papel. Estas son herramientas teóricas que no permiten las mediciones, como es el caso de la regla y el compás que generalmente usamos. La construcción de un objeto matemático garantizaba su existencia, no bastaba con definirlo, de ahí la importancia de las construcciones con regla y compás.
Aunque aparentemente Elementos es un libro de geometría plana y del espacio, y como tal se le conoce, hay que resaltar que allí encontramos también teoría de números y la llamada álgebra geométrica. La aparición de las magnitudes inconmensurables (léase números irracionales) hizo de la geometría, y no de la aritmética, como en el caso de la escuela pitagórica, el fundamento de la matemática. Los problemas de aplicación de áreas, como es el caso del teorema de Pitágoras, plantean problemas e igualdades algebraicos que hoy reconocemos en algunos casos como productos notables y que encontramos en los libros II y VI. Igualmente en el V encontramos la teoría de las proporciones y en los libros VII a X se presenta un tratamiento geométrico de la teoría de los números reales.
En la antigüedad se clasificaban las proposiciones a demostrar en problemas y teoremas. En las primeras se trataba de construir un objeto determinado, es el caso de la construcción de un triángulo equilátero o el trazado de perpendiculares o paralelas a una recta dada. En los teoremas se demuestran algunas propiedades de los objetos construidos, es el caso del teorema de Pitágoras que se presenta a continuación.
El teorema de Pitágoras en el libro I
El primer libro de Elementos tiene como objetivo central la demostración del teorema de Pitágoras (T.47) y su recíproco (T.48); contiene 23 definiciones y 48 teoremas. Todas las demostraciones siguen un patrón que resaltaremos en el caso del teorema de Pitágoras. Hemos tomado literalmente la versión que se encuentra en la traducción de Elementos de Gredos (1991), con el fin de estimular el uso de las fuentes primarias. Demostraciones del teorema se encuentran en múltiples fuentes secundarias y en los libros de texto. Animamos al lector a compararlas con la original.
Enunciado general: en los triángulos rectángulos el cuadrado del lado que subtiende al ángulo recto es igual a los cuadrados de los lados que comprenden el ángulo recto.
Enunciado particular: sea ABΓ el triángulo rectángulo que tiene el ángulo recto BAΓ. Digo que el cuadrado de BΓ es igual a los cuadrados de BA y AΓ.
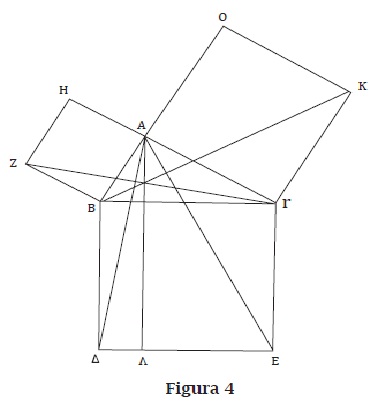
Construcción: trácese pues sobre BΓ el cuadrado BΔEΓ;, y a partir de BA, AΓ los cuadrados HB, ΘΓ[I, 46], y por el (punto) A, trácese AΔ una paralela a una de las dos (rectas) BΔ, Γ E [I, 31] y trácese AΔ, ZΓ, [P 1].
Demostración: Y dado que cada uno de los ángulos BAΓ y BAH es recto, entonces en una recta cualquiera BA y por un punto de ella, A, las dos rectas AΓ, AH no colocadas en el mismo lado hacen ángulos adyacentes iguales a dos rectos; por tanto, ΓA está en línea recta con AH.ΓI, 14Γ. Por la misma razón, BA también está en línea recta con AΓ. Y como el ángulo AB∧ es igual al (ángulo) ZBA - porque cada uno de ellos recto-añádase a ambos el (ángulo) AB∧; entonces el ángulo entero ΓBA es igual al (ángulo entero) entero ZBΓ ∧NC 2Γ; y como ΓB es igual a BΓ, y ZB a BA, los dos (lados) ΓB y BA, son iguales respectivamente a los dos (lados) ZB, BΓ; y el ángulo ΓBA es igual al ángulo ZBΓ; entonces la base ΓA es igual a la base ZΓ, y el triángulo AB∧ es igual al triángulo ZBΓ [I, 4] y el paralelogramo BΓ es el doble del triángulo AB∧: porque tienen la misma base BΓ y están entre las mismas paralelas BΓ, AΓ[I, 41]; pero el cuadrado HB es el doble del triángulo ZBΓ: porque tienen la misma base ZB y están entre las mismas paralelas ZB, HΓ [I, 41]; [pero los dobles de cosas iguales son iguales entre sí]; por tanto, el paralelogramo BΓ es también igual al cuadrado HB. De manera semejante, trazando las (rectas) AE, BK se demostraría que también el paralelogramo Γ∧es igual al cuadrado Γ∧; por tanto, el cuadrado entero BΓEΓ es igual a los cuadrados HB, ΓΓ∧NC 2Γ; Asimismo, el cuadrado BΓEΓ ha sido trazado a partir de BΓ, y los (cuadrados) HB, Γ∧ a partir de BA, AΓ. Por tanto el cuadrado de lado BΓ es igual a los cuadrados de los lados BA, AΓ.
Por consiguiente en los triángulos rectángulos el cuadrado del lado que subtiende al ángulo recto es igual a los cuadrados de los ángulos que comprenden al ángulo recto. Q.E.D.
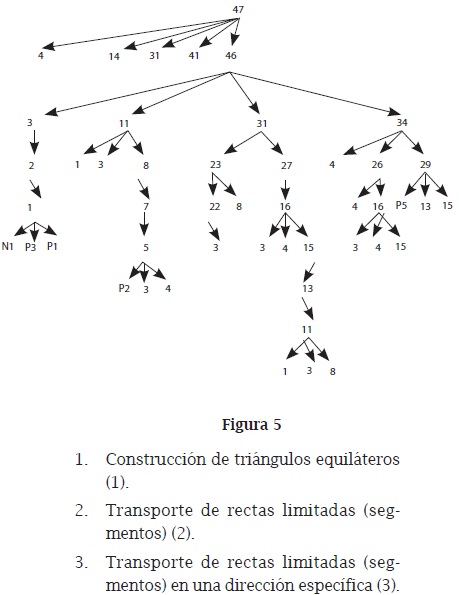
Uno de los primeros pasos en la demostración del teorema de Pitágoras es la construcción de cuadrados. Se trata de la proposición 46 en el libro I de los Elementos. En Sánchez (2006) se encuentra el análisis de la demostración y algunas reflexiones pedagógicas sobre la enseñanza de la geometría alrededor de este problema. En la figura 5 se encuentra un diagrama de ese análisis y a continuación una breve descripción del tema de cada uno de los teoremas involucrados. Obsérvese que todas las ramas del árbol terminan en los postulados y las nociones comunes o axiomas son los elementos de Elementos, son las raíces sobre las cuales está cimentado el árbol. Permite ver cómo funciona el sistema axiomático allí dado. A través del análisis (el razonamiento hacia atrás de la tesis a las hipótesis) que hemos hecho del teorema se puede apreciar el trabajo que debió hacer Euclides para encontrar los principios fundamentales, y entender por qué son esos y no otros.
- Construcción de triángulos equiláteros (1).
- Transporte de rectas limitadas (segmentos) (2).
- Transporte de rectas limitadas (segmentos) en una dirección específica (3).
- Primer caso de igualdad de triángulos (4).
- Teorema del triángulo isósceles (5).
- Unicidad en la construcción de un triángulo (7).
- Tercer caso de igualdad de triángulos (8).
- Bisección de un ángulo (9).
- Bisección de una recta limitada (10).
- Construcción de ángulos rectos (perpendiculares) (11).
- Una recta incidente sobre otra forma ángulos iguales a dos rectos (13).
- Dos rectas que con una misma recta dada determinan dos ángulos iguales a dos rectos, están sobre la misma línea recta (14).
- Ángulos opuestos por el vértice son iguales (15).
- Teorema del ángulo externo (16).
- En todo triángulo el lado mayor subtiende al ángulo mayor (18).
- En todo triángulo el ángulo mayor es subtendido por el lado mayor (19).
- Desigualdad triangular (20).
- Construcción de un triángulo cualquiera (22).
- Transporte de ángulos (23).
- Segundo caso de igualdad de triángulos (26).
- Existencia de paralelas (27).
- Propiedades de las paralelas (29).
- Trazado de paralelas (31).
- En un paralelogramo los lados y los ángulos opuestos son iguales, y, el diámetro divide en partes iguales al paralelogramo. (34).
- Los paralelogramos que están sobre la misma base y entre las mismas paralelas son iguales entre sí (35).
- Los triángulos que están sobre la misma base y entre las mismas paralelas son iguales entre sí (37).
- Si un paralelogramo y un triángulo están sobre la misma base y entre las mismas paralelas, el paralelogramo es doble del triángulo (41).
- Construcción de cuadrado (46).
Hemos resaltado el teorema 29 debido a que es el primero en que se usa el quinto postulado. Esto ha hecho pensar a los historiadores que Euclides era consciente de la importancia y dificultad de este postulado y por eso aplazó su uso lo máximo posible.
La estructura de Elementos. Sistema o método axiomático
La estructura anterior es lo que se conoce como sistema o método axiomático. Consiste en organizar una teoría de la siguiente manera:
- Se definen los objetos, o nociones a estudiar.
- Se fijan unos principios básicos de la teoría sobre los objetos
- o nociones básicas que se suponen evidentes y por eso se aceptan sin demostración.
- Se establecen unos principios lógicos, las nociones comunes o axiomas, que se suponen válidos para todas las ciencias.
- A partir de los elementos anteriores se deducen las proposiciones (propiedades de los objetos de estudio) de la teoría que se está axiomatizando.
Éste es el gran aporte de Euclides a las matemáticas y a la ciencia en general, la sistematización de unos conocimientos de tal manera que a partir de unos pocos principios se puedan deducir las proposiciones de la teoría; así, si los principios iníciales son verdaderos y se siguen cuidadosamente los pasos lógicos, las consecuencias de esos principios, los teoremas, resultan igualmente verdaderos.
El contenido de la obra Elementos
Este apartado por contenido se refiere a ciertos aspectos que podemos apreciar más allá de los contenidos explícitos encontrados en cada una de sus proposiciones.
Construcciones con regla y compás
En Elementos se encuntra la construcción de varios polígonos regulares: de tres y cuatro lados en el libro I; de cinco, seis y quince lados en el libro IV; la proposición I-11 dice cómo se trazan perpendiculares, y la I-27 cómo se trazan paralelas. Encontramos igualmente cómo inscribir y circunscribir polígonos en una circunferencia. Todas las construcciones requeridas para las demostraciones se hacen con la regla y el compás euclidianos (los tres primeros postulados)11.
Sin embargo, son muchas las figuras geométricas que no son construibles con regla y compás; es el caso de mayoría de los polígonos regulares12 o las cónicas. Por siglos se intentó demostrar con regla y compás los famosos problemas de la duplicación del cubo (construir un cubo de volumen doble de un cubo dado), la cuadratura del círculo (construir un cuadrado de área igual al de un círculo dado) y la trisección del ángulo (dividir un triángulo en tres partes iguales). Problemas de aparente simplicidad por su enunciado pero imposibles de resolver con la regla y el compás euclidianos como fue demostrado en el siglo XIX13. Los griegos se dieron cuenta que esas construcciones no eran posibles y por eso se inventaron otras herramientas curvas llamadas mecánicas, como la concoide, la cisoide, la espiral o la cuadratriz que sí permiten resolver los problemas14.
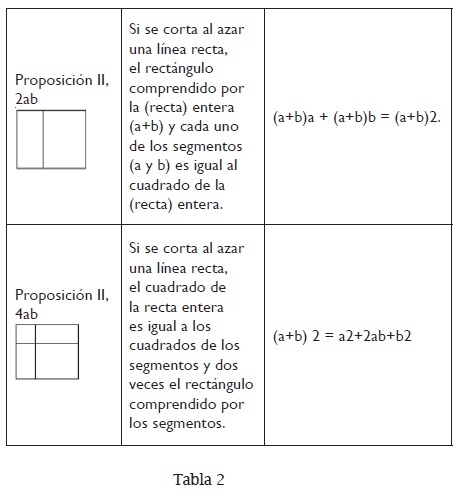
Álgebra geométrica
En el segundo libro de Elementos se presentan varios problemas y teoremas sobre la "aplicación de áreas", consistentes en hallar una figura con la misma área de otra dada. La aplicación de áreas recibió a partir de 1886 con Zeuthen15 el nombre de álgebra geométrica que aunque problemático, pues tiene más de una interpretación, busca establecer la traducción de los teoremas del libro II en expresiones algebraicas. Algunos ejemplos sencillos:
Teoría de las proporciones
El libro V contiene la teoría de las proporciones de Eudoxio; es uno de los libros más apreciados de Elementos, ya que aquí se tratan con el mismo rasero las magnitudes conmensurables y las inconmensurables por medio de las nociones de razón y de proporción. Inclusive los historiadores rastrean en este libro los fundamentos de las definiciones de Weierstrass y de Dedekind de número real16. La noción de proporción fue clave en la arquitectura y en general en el arte griego; como caso especial tenemos la proporción áurea en la cual se establece que el todo es a la parte mayor como la parte mayor es a la parte menor. Si suponemos que b es la parte mayor y a la parte menor de un segmento AB tendríamos que a+b:b::c:a; esta proporción nos lleva al número φ = (1+√5)/2, uno de los números más distinguidos de la matemática al lado de √2, π, e, 0, 1 y √-1.
Teoría de números
Los libros VII, VIII y IX tratan de teoría elemental de números. El libro VII comienza con la definición de número: "un número es una multiplicidad de unidades" y con lo que hoy conocemos como el algoritmo de Euclides. En el IX encontramos una proposición equivalente al teorema fundamental de la aritmética (proposición 14) y la demostración de la infinitud de los números primos (proposición 20). El X trata sobre los irracionales, y es llamado la cruz de los matemáticos por el nivel de dificultad que tiene para asimilarlo.
La geometría del espacio y los sólidos platónicos
Los libros XI, XII y XIII contienen la geometría del espacio; la construcción y algunas propiedades de los poliedros regulares llamados sólidos platónicos: tetraedro, cubo, octaedro, icosaedro y dodecaedro. Culmina el libro XIII y así Elementos con la demostración de la no existencia de ningún otro poliedro regular.
Las fortalezas y debilidades de Elementos y sus consecuencias
A continuación se muestra cómo algunas aparentes debilidades de Elementos se convirtieron en motivo para crear otras áreas de la matemática. Se trata de
- El quinto postulado y las geometrías no euclidianas.
- Las curvas no planas (las cónicas y las curvas lineales) y la geometría analítica.
- Las fallas lógicas y los Fundamentos de la Geometría, de Hilbert.
El quinto postulado y las geometrías no euclidianas
La complejidad del quinto postulado en relación con los otros cuatro es clara. Por ello desde la Antigüedad se le consideró menos evidente que los otros y se intentó probarlo a partir de ellos. La historia de los intentos por demostrar el quinto postulado a partir de los otros es una de las historias más interesantes de la matemática, entre otras razones por la cantidad de matemáticos y aficionados a ella que intentaron hacerlo. Muchos creyeron haberlo logrado; sin embargo, la demostración usaba de manera explícita o implícita otro teorema, o axioma, con lo cual la demostración dejaba de serlo; la proposición usada resultaba ser equivalente al quinto postulado, con lo cual había de alguna manera un círculo vicioso.
De todos los intentos realizados se destaca el de Gerolamo Saccheri (16671733), jesuita de la Universidad de Pavia, quien intentó hacer la demostración por reducción al absurdo. Su trabajo, titulado Euclides vindicado de toda culpa, muestra claramente los propósitos del autor. Pero sus creencias le impidieron ver lo que había encontrado, lo que hoy conocemos como geometrías no euclidianas.
John Play Fair (1748 -1819) propuso como axioma que por un punto exterior a una recta pasara una sola paralela. Este enunciado fácil de entender y aceptar por su evidencia se popularizó como el quinto postulado de Euclides. Su negación nos lleva a dos posibilidades: que por un punto exterior a una recta pasen más de una paralela o que por un punto exterior a una recta no pasen rectas paralelas, lo que llevó al estudio de geometrías en las que no se tenía el quinto postulado sino alguna de sus negaciones. Bolyai estudió la geometría que aceptaba la primera negación y un poco más tarde Riemann estudió la geometría que postulaba la segunda negación. Estas geometrías se conocen como geometrías no euclidianas.
Janos Bolyai (1802-1860) tituló su trabajo Ciencia absoluta del espacio y fue publicado hacia 1830. Fue conocido por Gauss y fuertemente elogiado por él, pues había tenido ideas parecidas. Nicolai Lobachevsky (1792-1856) denominó su trabajo geometría imaginaria y publicó entre 1829 y 1855 varios trabajos sobre el tema. Estos trabajos fueron aceptados apenas como especulaciones teóricas sin fundamento en la realidad. Dos trabajos, uno del italiano Eugenio Beltrami (18351899) y otro del alemán Felix Klein (18491925) dieron un modelo a esa geometría que mostró su consistencia. Con estos trabajos las reticencias de los matemáticos fueron superadas y el valor de los trabajos de Bolyai y de Lobachevsky ampliamente reconocido.
Por otro lado, Riemann (1826-1866), uno de los matemáticos más ilustres del siglo XIX, interpretó el segundo postulado en el sentido de que la recta no sea de longitud infinita sino ilimitada. Esta propiedad la cumple la circunferencia. Además observó que la experiencia no da evidencias sobre la existencia de paralelas; con estas ideas construyó la geometría esférica en la que por un punto exterior a una recta no pasan paralelas, en la cual la suma de los ángulos de un triángulo es mayor que dos rectos. Su modelo la superficie de la esfera.
La creación de las geometrías no euclidianas marcó un punto de corte epistemológico en la matemática, la ciencia en general y la filosofía. Estas teorías mostraron que no hay verdades absolutas en matemáticas y cuestionó, por tanto, el concepto de verdad17. Los matemáticos se preguntaron ¿qué es geometría? Y de esas reflexiones resultó el Programa de Erlangen liderado por Felix Klein, en el cual se dio una definición de geometría como el estudio de las propiedades que permanecen invariantes por un grupo de transformaciones. Bajo este criterio la geometría euclidiana es el estudio de las propiedades que permanecen invariantes por medio del grupo formado por traslaciones, rotaciones y reflexiones18.
Las curvas no planas (las cónicas y las curvas lineales) y la geometría analítica
Nos devolvemos al siglo XVII, para dar cuenta de la aparición de lo que hoy conocemos como geometría analítica. Habíamos anotado que en Elementos de Euclides se había sistematizado gran parte de la matemática de su época pero no toda. En particular queda por fuera toda la geometría que tiene que ver con las cónicas: parábolas, hipérbolas,
Los antiguos griegos clasificaron las curvas en tres grupos: planas las que se podían construir con regla y compás, sólidas las cónicas y lineales las demás. Cada una de ellas caracterizada por ciertas propiedades geométricas, expresadas en muchos casos en forma de proporciones. Apolonio de Perga (c. 262-169 a.C), en su obra Cónicas, estudió las curvas sólidas y es, junto con los Elementos de Euclides, uno de los grandes legados de la matemática griega.
En el siglo XVII la teoría heliocéntrica de Copérnico y de Kepler requería de un mejor conocimiento de la curvas, particularmente de las elipses. Por otro lado se requería no solo conocer la trayectoria que seguiría la bala de un cañón, sino la máxima altura que alcanzaría y la distancia a la que llegaría. El siglo XVII pedía información cuantitativa, numérica, de vital importancia para la práctica. Por otro lado, los famosos problemas de construcción de los griegos: la duplicación del cubo (construir con regla y compás un cubo de volumen doble de un cubo dado), la trisección del ángulo (dividir con regla y compás y ángulo en tres partes iguales) y la cuadratura del círculo (construir con regla y compás un cuadrado de área igual a la de un círculo dado) fueron resueltos en la Antigüedad por medio de curvas especiales como la cuadratriz de Hipias, la espiral de Arquímedes, o la concoide de Nicómaco. Curvas llamadas mecánicas por Platón, pues requerían aparatos distintos de la regla y el compás para ser construidas forman parte de las curvas lineales. Con la geometría analítica todas ellas pasarán a ser representadas por medio de ecuaciones algebraicas.
Se debe a René Descartes (1596-1650) y Pierre de Fermat (1601-1655) la creación de la geometría analítica. Aquí se tratará al aporte de Descartes quienen su famoso tratado Discurso del método, en 1637, añade al final un apéndice titulado "Géométrie", compuesto de tres capítulos:
- El primero trata de los "Problemas que pueden resolverse sin emplear más que círculos y líneas rectas".
- El segundo se titula "De la naturaleza de las líneas curvas". Trata especialmente de las curvas de grado superior a dos y, sobre todo, de la construcción y propiedades de tangentes y normales a las curvas.
- El tercero, "Sobre la construcción de problemas sólidos y super sólidos", trata del estudio de la resolución de ecuaciones de grado mayor a dos, discusión de sus raíces y relaciones entre los coeficientes.
En su "Geométrie", Descartes afirma que cualquier problema de geometría puede reducirse fácilmente a términos tales que el conocimiento de las longitudes de determinados segmentos es suficiente para su resolución.
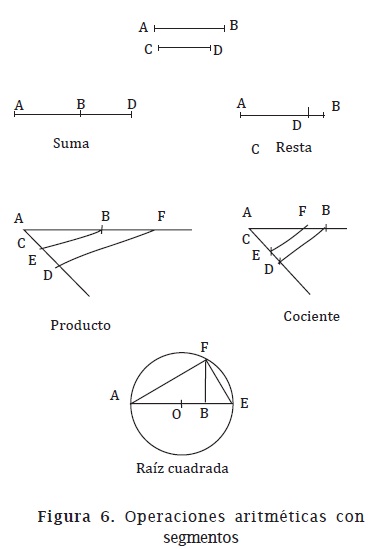
En Elementos se puede observar cómo el producto de dos longitudes resulta en un rectángulo. Descartes hará que tanto la suma, como la resta, la multiplicación o la división de dos segmentos sea un segmento y que la raíz cuadrada de un segmento también sea un segmento usando las herramientas euclidianas. De esta manera muestra que las operaciones de la aritmética pueden hacerse con regla y compás. Así, dado un segmento AB, el producto AB×AB no es un cuadrado sino un segmento y AB×AB×AB no es un cubo sino otro segmento. De ahí que a las expresiones x2 o x3 las llamemos x al cuadrado o x al cubo.
Sean AB y CD dos segmentos. En la figura 6 se razona usando la semejanza de triángulos. Para producto y cociente se toma como unidad de medida CE y para la raíz cuadrada, el segmento BE.
- Adición de segmentos (figura 6A): al extremo B del segmento AB se "traslada" el segmento CD. De esta manera se obtiene AD = AB + CD.
- Resta de segmentos (figura 6B): el segmento CD se "traslada" al segmento AB de tal manera que C coincida con A. De esta manera se obtiene BD = AD - CD.
- Producto de segmentos (figura 6C): se colocan los dos segmentos de tal manera que formen un ángulo. Sobre el lado CD se escoge la unidad CE y se une E con B. Luego se traza una paralela a EF por D, y se marca el punto F de corte de la paralela con la prolongación del segmento AB. Se obtienen dos triángulos semejantes y de allí se deduce que AB:CE = AF:CD. Luego AB × CD= AF.
- División de segmentos (figura 6D): como en el caso anterior se colocan los dos segmentos de tal manera que formen un ángulo. Sobre el lado CD se escoge la unidad CE y se une D con B. Luego se traza una paralela a DB por E, y se marca el punto F de corte de la paralela con el segmento AB. Se obtienen dos triángulos semejantes y de allí se deduce que AB:CD = AF:CE Luego AB/CD = AF.
- Raíz cuadrada de un segmento (figura 6E): dado el segmento AB se prolonga en una unidad BE. Luego se obtiene el punto medio O del segmento AE. Se traza una circunferencia con centro en O y radio OE. A partir de B se traza una perpendicular a AE que corta a la circunferencia en F. Se une F con A y F con E. Se obtienen tres triángulos rectángulos semejantes AFE, AFO y OFE. De la semejanzas de triángulos se deduce que AB:BF=BF:BE. Luego AB×BE = (BF)2. De donde BF = √AB.
Los números que se pueden construir con regla y compás se llaman números construibles. Estos incluyen a todos los naturales a partir del dos, los racionales positivos y todas las raíces cuadradas de los números ya construidos.
Para Descartes, el álgebra, que había avanzado en unos años atrás con los trabajos de Cardano (1501-1576), Tartaglia (1499-1557) y Viéte (1540-1603), mejoraba la eficiencia del razonamiento. Mientras la geometría contenía la verdad del universo, el álgebra ofrecía la ciencia del método. Su método lo llevará a afirmar que una ecuación puede tener tantas raíces como dimensiones tiene el grado de la ecuación. Esta es una primera formulación del teorema fundamental del álgebra. Como anotamos, Descartes se propuso analizar las curvas con líneas rectas. Procedía como se muestra en la figura 7.
Escogía unos puntos sobre la curva, P1, P2, ...Pn, trazaba un recta horizontal H y observaba cómo cambiaban las distancias de los puntos escogidos con la línea horizontal. Luego consideraba la distancia de los segmentos que se formaban con los puntos de la curva y la línea horizontal P1Q1, P2Q2, PnQn, con respecto a un punto fijo O.
De esta manera, la posición de los puntos de la curva quedaba especificada por los números de las longitudes de los dos segmentos determinados. Con lo anterior, hallaba la ecuación, la resolvía, la interpretaba geométricamente.
Las fallas lógicas y los fundamentos de la geometría de Hilbert
Son varias las fallas lógicas que se han encontrado en Elementos desde el primer teorema sobre la construcción de un triángulo equilátero en el cual no está justificado que la intersección de dos círculos sea un punto. O en la demostración del cuarto, el teorema LAL de congruencia de triángulos, en el que se usa que si se traslada un triángulo sobre otro de tal manera que coincidan dos lados y el ángulo comprendido deben coincidir los demás lados y ángulos del triángulo. Este teorema usa una estrategia no contemplada en los postulados de construcción y además supone la homogeneidad del espacio, no contemplada explícitamente por Euclides. Varias de sus definiciones no son adecuadas como las de punto y línea, y jamás son usadas en la obra. En Trudeau (1987) se presentan las fallas y una solución al estilo de Euclides. Hilbert, en cambio, dados los alcances de la matemática en el siglo XIX y, particularmente, de la geometría, propondrá su famoso sistema en los Fundamentos de la geometría (1996) que dará origen a lo que hoy conocemos como un sistema formal (Campos, 2008, pp. 239-364).
Aspectos lógicos y filosóficos de los Elementos
Para terminar nuestra reflexión sobre las bondades de hacer un recorrido histórico por la historia de la geometría como recurso didáctico, es importante revisar algunos de los aspectos lógicos y filosóficos que presenta la obra Elementos.
La noción de existencia
Resaltamos cómo la construcción de las figuras con regla y compás tiene como objetivo garantizar que los objetos definidos son efectivamente "realizables", existen. A partir de ahí podemos estudiar y demostrar sus propiedades y relacionarlos con otros "objetos" matemáticos.
La lógica en los Elementos
Si por algo se ha caracterizado la obra de Euclides es por su rigor lógico, aunque con el paso del tiempo se le hayan descubierto fallas significativas. Allí encontramos varios de los métodos tradicionales en matemáticas para hacer demostraciones como son el método por reducción al absurdo, el método de exhaución, y el método analítico-sintético. Su forma de hacer demostraciones usa de manera implícita lo que llamaríamos la regla de generalización universal, ya que aunque razona sobre una figura particular, esta es un caso arbitrario lo que le permite luego hacer la generalización requerida. Las fallas lógicas que se encuentran desde el primer teorema pueden ser subsanadas añadiendo nuevos postulados como lo ha hecho, por ejemplo, Trudeau (1987).
La noción de demostración en los Elementos
Un recorrido por Elementos nos muestra cómo sigue un patrón en sus demostraciones que resaltamos en el caso del teorema de Pitágoras. Enunciado general, figura, enunciado particular, construcción y demostración. En esta última parte se hace siempre referencia a proposiciones antes demostradas, o a los postulados dados desde el comienzo. Es esencialmente lo que hoy entendemos por una demostración matemática.
El primer sistema axiomático
En la actualidad se discute si en Elementos se halla, efectivamente, el primer sistema axiomático de la historia, por algunas de las deficiencias encontradas. Quienes dudan de que así sea tienen como modelo el sistema axiomático al estilo Hilbert (1986) en sus Fundamentos de geometría. Se dice que el de Euclides es un sistema axiomático material, pues las nociones básicas tienen contenido, mientras que la axiomática de Hilbert es formal, ya que las nociones primitivas o indefinidas en este último autor se presentan como sistemas de entes que se caracterizarán a través de los axiomas y podrían tener más de una interpretación.
El infinito
La presencia del infinito es clara en Elementos, así la palabra no aparezca de manera explícita. Veamos algunos ejemplos.
La definición 23 establece que son líneas paralelas las que estando en el mismo plano y siendo prolongadas indefinidamente por ambos lados no se encuentran una a otra en ningún punto. El segundo postulado establece que una recta puede prolongarse indefinidamente en línea recta y la proposición 20 del libro IX establece que hay más números primos que cualquier cantidad propuesta de números primos.
Espacio físico y espacio matemático
La aparición de las geometrías no euclidianas mostró que la creencia generalizada de que la geometría euclidiana era la teoría del espacio físico quedó completamente revaluada. El espacio matemático es una construcción teórica que, entre otras cosas, puede tener tantas dimensiones como se quiera.
El impacto de los Elementos en áreas diferentes a la matemática
Desde la introducción de este artículo resaltamos la importancia que la obra de Euclides ha tenido en la historia de nuestra civilización. Entre los grandes pensadores que la tuvieron como modelo están Kant y Spinoza. El primero la toma como modelo en su famosísima obra La crítica de la razón Pura. Por su parte, Spinoza organiza su Ética al estilo de los Elementos y Newton considera a Euclides como uno de los gigantes sobre los que está parado para realizar su trascendental obra. Hemos visto cómo, ya sea por sus fortalezas o debilidades, la historia de la matemática hace siempre referencia a la obra euclidiana. El carácter hipotético deductivo que ha caracterizado a la matemática hasta hoy viene esencialmente de esta obra.
Conclusiones
Al presentar la famosa obra de Euclides en los múltiples aspectos que entraña, el educador puede sacarle provecho didáctico desde múltiples aspectos como son:
Apreciación por parte del estudiante de lo que es una demostración matemática y lo que significa rigor en un razonamiento
Aunque, como vimos, Elementos tiene deficiencias lógicas, éstas se detectaron de manera sistemática a finales del siglo XIX cuando el rigor en las demostraciones era una prioridad para los matemáticos de la época. Se había comenzado a desarrollar la lógica matemática que permitía ese rigor y, entre otras cosas, la aparición de la escuela formalista de Hilbert. Pero, por siglos, fue modelo de rigor y al nivel elemental para empezar a entender lo que es una demostración, sin necesidad de un curso de lógica.
El álgebra geométrica
Se ha convertido en un recurso didáctico muy utilizado para la enseñanza de la resolución de ecuaciones de segundo grado y para visualizar la factorización de un polinomio de segundo grado. Profundizar en qué casos son visibles y cuáles no, y por qué permitirá al instructor igualmente entender el desarrollo del álgebra en los casos analizados por personajes de la historia como Cardano o Tartaglia. Usualmente se enseñan los casos factibles, los factorizables y visibles, y se dejan de lado los demás. ¿Por qué? Una reflexión con los estudiantes sobre este tópico les permitiría ver por qué factorizar no es un proceso algorítmico, requiere de entrenamiento y hay casos no factorizables.
Comprensión de lo que es un sistema axiomático
¿Por qué la matemática tiene como esencia los sistemas axiomáticos, como afirma Newton da Costa? Elementos nos permite aproximarnos a una respuesta. Las demostraciones no pueden ser infinitas, hay que parar en algún momento y esos son los principios básicos sobre los que se armará el sistema. Encontrarlos es toda una tarea de reflexión analítica. La pregunta sobre cómo se construye un cuadrado busca ilustrar este tipo de reflexión. El mismo ejercicio se puede hacer con cualquier teorema de la obra.
Aclaración de ideas erradas sobre la obra de Euclides
Existen múltiples prejuicios sobre la obra de Euclides que hay que considerar como son:
- En Elementos se recoge toda la matemática de su época. El saber que hay matemática por fuera de Elementos y buena matemática permite comprender muchos aspectos sobre las distintas áreas de la matemática de la época, y cómo los vacíos o prejuicios que habría sobre distintos aspectos permiten avanzar en el desarrollo de las matemáticas con el surgimiento de nuevas áreas.
- La geometría euclidiana, la de Elementos, es geometría plana.
- El quinto postulado de Euclides es: por un punto exterior a una recta pasa una paralela. Con esto se busca mostrar cómo se va transformando una teoría y cómo un enunciado intuitivamente más claro permite ver propiedades y abrir puertas para nuevos resultados.
Esperamos haber motivado suficientemente con este trabajo al lector en la historia de la geometría y en el estudio de la obra de Euclides y sus interesantes consecuencias en la historia de las matemáticas. En sus manos está sacarle buen provecho para su práctica docente.
Pie de página
1Es famosa la frase de Jean Dieudonné "Euclides debe irse" pronunciada en 1959 en el Seminario de Royamount, Francia, en el que se discutía sobre cómo mejorar la enseñanza de las matemáticas. En este seminario se acordó introducir la matemática moderna en la enseñanza de las matemáticas en los niveles básico y medio.
2Para ampliar, véase: Fletcher (1971), Gerdes (1988), Revuz(1986) y Chi Kai(2001).
3Los Sulbasutras, en los que se dan normas para la construcción de altares, es un apéndice de los textos sagrados del pueblo Védico que entró en la India alrededor del año 1500 a.C.
4Más detalles pueden consultarse en Sánchez (1994), Heath (1981) o Knorr (1986).
5En Colombia, por ejemplo, el ingeniero Manuel H. Peña publicó, en 1887, una Geometría práctica. Lecciones de agrimensura, topografía y nivelación.
6Bruño fue el pseudónimo de San Miguel Febres Cordero, un religioso de los Hermanos de La Salle canonizado por el papa Juan Pablo II en 1984. Sus textos fueron usados en América Latina en el siglo XX.
7Otra versión del teorema de Pitágoras es en un triángulo rectángulo cuyos lados tienen longitudes a, b, c donde c es la longitud de la hipotenusa se cumple que a2+b2=c2. Obsérvese que esta versión privilegia el aspecto algebraico del teorema sobre el geométrico que no se refiere a los valores numéricos de las magnitudes consideradas. Los estudiantes, usualmente, recuerdan la fórmula, que no es válida para cualesquiera valores de a,b y c, y no tienen claro el contexto en el cual sí vale.
8Requeriría justificar por qué los ocho triángulos en cuestión son iguales o congruentes, y por qué la figura del centro en la figura 2 es efectivamente un cuadrado.
9La historia de cómo se trasmitió la obra a través de los tiempos y las traducciones y ajustes que se le fueron haciendo por los transcriptores y traductores a las diferentes lenguas es bien interesante, sin embargo no es el caso detenernos en este punto. La primera traducción directamente del griego al español es la de Gredos (Euclides, 1991), y es la que usaremos de referencia en este artículo.
10No se tienen datos precisos sobre la vida de Euclides. Se sabe por autores antiguos que vivió en el siglo III a.C., y fue profesor de matemáticas en el Museo de Alejandría. Euclides escribió varias obras de las cuales quedan solamente Elementos y Datos; este último parece ser un texto auxiliar al primero.
11Actualmente existen programas adecuados de computador que permiten ver las construcciones con regla y compás, como son Ruler and Compas y Cabrí.
12En 1796 Gauss demostró que el polígono regular de 17 lados era construible con regla y compás. Cinco años más tarde en su libro Disquisitiones Arithmeticae formuló una condición suficiente para la constructibilidad de los polígonos regulares, y es que un polígono regular de N lados es construible con regla y compás si N = 2kp1p2...pn donde k≥1 y los pi son números primos de la forma 2m+1 distintos entre sí. Wantzel en 1837 demostró que la condición era además, necesaria.
13Con el desarrollo del álgebra en el siglo XIX se analizaron las ecuaciones que conllevan a los famosos problemas de construcción. La duplicación del cubo y la trisección del ángulo se formulan por medio de ecuaciones de tercer grado, a saber: x3= 2V y y33by2-3a2y+a2b = 0 ; la cuadratura del círculo plantea la ecuación x2 = 2 πr , pero π no es construible por ser un número trascendente.
14Puede consultarse Sánchez (1994), Heath (1981) y Knorr (1986).
15Hieronymus Zeuthen (1839-1920) matemático danés.
16En Grattan Guinness (1996) y Knorr (1992) se encuentran reflexiones interesantes sobre este tema.
17Un excelente artículo sobre este tema se encuentra en Kline (1992).
18Más detalles en Campos (2008, pp. 203-207). elipses. Son las figuras que se obtienen al cortar un cono recto de diferentes maneras, además del círculo.
Referencias
Bruño, G. (s.f.). Geometría superior. Paris: [s..e] [ Links ]
Bruño, G. (1921).Elementos de Geometría. México: Librería de la Vda. de C. Bouret. [ Links ]
Campos, A. (2008). Introducción a la historia y la filosofía de las matemáticas. Bogotá: Universidad Nacional de Colombia. [ Links ]
De Guzmán, M. (1993). Tendencias innovadoras en educación matemática. Organización de Estados Iberoamericanos para la Educación, la Ciencia y la Cultura - OEA. [ Links ]
Euclides (1991).Elementos. Barcelona: Gredos. [ Links ]
Eves, H. (1992). An Introduction to the History of Mathematics. 6a. ed. Filadelfia: The Saunders Series. [ Links ]
Fletcher, T. (1971). The Teaching of Geometry Present Problems and Future Aims. Educational Studies in Mathematics, 3(3-4), 395-412. [ Links ]
Gerdes, P. (1988). On Culture, Geometrical Thinking and Mathematics Education. Educational Stuidies in Mathematics, 19, 137-162. [ Links ]
Gerdes, P. (2001). Origins of Geometrical Thought in Human Labor. Nature, Society and Thought, 14,391-418. [ Links ]
Grattan Guinnes, I. (1996). Numbers, Magnitudes, Ratios, and Proportions in Euclid's Elements: How Did He Handle Them?Historia Mathematica, 23, 355-375. [ Links ]
Heath, S. (1981). A History of Greek Mathematics. Nueva York: Dover Publications Inc. [ Links ]
Hilbert, D. (1996). Fundamentos de la geometría. Madrid: CSIC. [ Links ]
Kline, M. (1959). Mathematics and the Physical World. Nueva York: Dover Publications Inc. [ Links ]
Kline, M. (1992). Matemáticas para estudiantes de humanidades. México: Fondo de Cultura Económica. [ Links ]
Knorr, W. (1986).The Ancient Tradition of Geometric Problems. Boston: Birkhauser. [ Links ]
Knorr, W. (1992). De exhausción a cortaduras: primeras etapas de la teoría griega de las proporciones. Mathesis, 8, 1-12. [ Links ]
Legendre, A. (1866). Elementos de geometría. Trad. Luis María Lleras. Bogotá Imprenta de Gaitán. [ Links ]
Loria, G. (1902). Sketch of the Origin and Development of Geometry Prior to 1850.The Monist, 13(1), 80-102. [ Links ]
Mitchellu, G. (1938). The Study and Teaching of the History of Mathematics. National Mathematics Magazine, 13(1), 22-29. [ Links ]
Moise, E. (1963). Elementary Geometry from an advanced stand point. Boston: Addison- Wesley. [ Links ]
Morris, K. (1981). Mathematics and the Physical World. Nueva York: Dover Publications. [ Links ]
Revuz, A. (1986). El lugar de la geometría en la enseñanza de las matemáticas. En: J. Piaget. La enseñanza de las matemáticas modernas (pp. 291-297). Madrid: Alianza Editorial. [ Links ]
Sánchez, C.H. (1994). Los famosos problemas de construcción de la geometría griega y su historia en Colombia. Bogotá: Universidad Nacional de Colombia. [ Links ]
Sánchez, C.H. (2006). ¿Cómo se construye un cuadrado? Lecturas Matemáticas, 27(1), 29-44. [ Links ]
Seidenberg, A. (1952). The Ritual Origin of Geometry. Archive of the History of Exact Sciences, 1(5), 488-527. [ Links ]
Schulmaister, M. (18 de diciembre de 2008). [Reseña del libro La enseñanza de la geometría por S. García Peña y O.L. López Escudero ]. Recuperado el 3 de marzo de 2011 de: http://www.oei.es/noticias/spip.php?article4073. [ Links ]
Toumassis, C. (1990). The EPOS of Euclidean Geometry in Greek Secondary Education (1836.1985): Pressure for Change and Resistance. Educactional Studies in Mathematics, 21(6), 491-508. [ Links ]
Trudeau, R. (1987). The Non-Euclidean Revolution. Boston: Birkhauser. [ Links ]
Vega, L. (1990). La trama de la demostración. Madrid: Alianza Editorial. [ Links ]