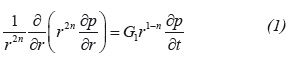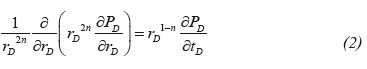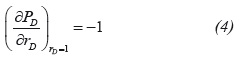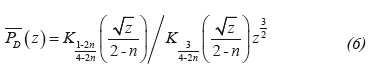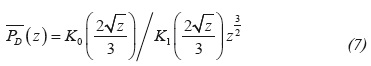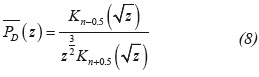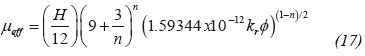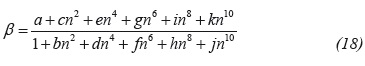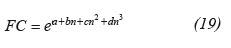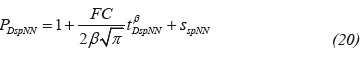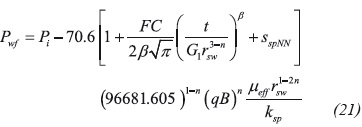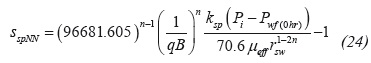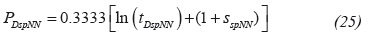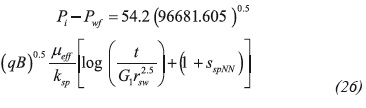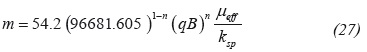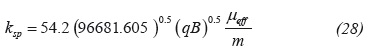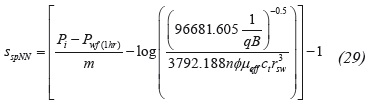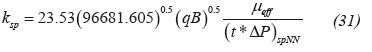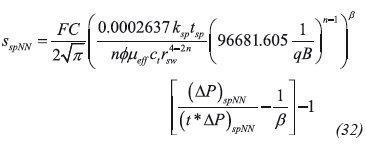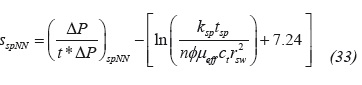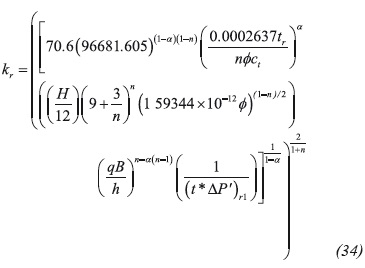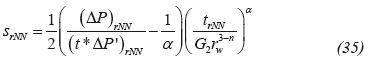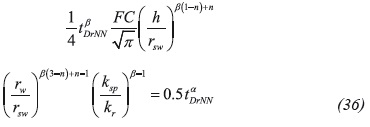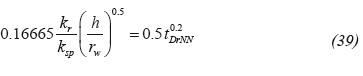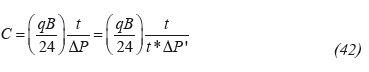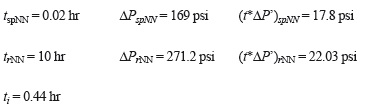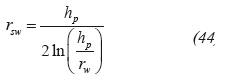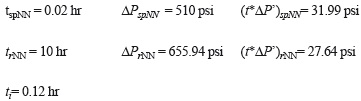TRANSIENT PRESSURE ANALYSIS FOR VERTICAL WELLS WITH SPHERICAL POWER-LAW FLOW

ANÁLISIS DE PRESIÓN TRANSITORIA PARA POZOS VERTICALES CON FLUJO ESFÉRICO LEY DE POTENCIA

Freddy-Humberto Escobar^1*, Javier-Andrés Martínez¹ and Luis-Fernando Bonilla¹

¹Universidad Surcolombiana, Neiva, Huila, Colombia

E-mail: fescobar@usco.edu.co jandres@usco.edu.co fbonilla@usco.edu.co

(Received Jun. 08, 2012; Accepted Oct. 31, 2012)

^*To whom correspondence should be addressed

ABSTRACT

Heavy oil is considered nowadays as one of the unconventional reservoirs of main interest in the oil industry. Some of them display non-Newtonian pseudoplastic behavior which mathematical modeling differs from the conventional case and, therefore, the flow regimes display some particular behaviors. Fracturing fluids, foams, some fluids for Enhanced Oil Recovery (EOR) and drilling muds can also fall into this category. The spherical/hemispherical flow mainly caused by partial completion/penetration deserves a particular treatment for pseudoplastic flow. A single research for this case was found in the literature to introduce only its mathematical model.

The pressure and pressure derivative behavior of spherical/hemispherical flow behavior of a slightly compressible, non-Newtonian power-law fluid (pseudoplastic) is studied in this work and conventional and Tiab's Direct Synthesis (TDS) methodologies are extended for well test interpretation purposes. For pseudoplastic spherical/ hemispherical flow, the slope of the pressure derivative is no longer -½, besides it changes with the value of flow behavior index n, which indicates that the interpretation of pressure data for the dealt systems through the use of traditional methods should not be accurate. New Equations are introduced to estimate spherical/ hemispherical permeability and spherical/hemispherical skin factor for the systems under consideration. The Equations were successfully verified by its application to synthetic cases.

Keywords: Pseudoplastic fluid, Consistency, Power-law, Radial flow, Partial completion, Partial penetration, Well tests, Transient pressure.

RESUMEN

Los crudo pesados son considerados actualmente como una clase de yacimientos no convencional de mayor interés para la industria petrolera. Algunos de ellos muestran un comportamiento no Newtoniano pseudoplástico cuyo modelo matemático difiere del caso convencional y por ende, los regímenes de flujo presentan algunos comportamientos particulares. Los fluidos de fracturamiento, las espumas, algunos fluidos usados en recobro mejorado y los lodos de perforación también caen en esta categoría. El flujo esférico/hemisférico causado por completamiento/penetración parcial merece un tratamiento especial para flujo pseudoplástico. Se encontró para este caso una sola investigación en la literatura que solo introduce el modelo matemático.

En este trabajo se estudia el comportamiento de la presión y la derivada de presión para flujo esférico/hemisférico de un fluido ligeramente compresible, no Newtoniano ley de potencia (pseudoplástico) y se extienden la metodologías convencional y Tiab's Direct Synthesis (TDS) para propósitos interpretativos de pruebas de pozos. En flujo esférico/hemisférico pseudoplástico, la pendiente de la curva de la derivada ya no es de -½, es más cambia con el valor del índice de comportamiento de flujo n, lo que indica que la interpretación de datos de presión para los sistemas en cuestión usando métodos tradicionales no sería exacto. Se introducen nuevas ecuaciones para estimar la permeabilidad esférica/hemisférica y el factor de daño esférico/hemisférico para tales sistemas. Las ecuaciones se verificaron satisfactoriamente con casos simulados.

Palabras clave: Fluido pseudoplástico, Consistencia, Ley de potencia, Flujo radial, Completamiento parcial, Penetración parcial, Análisis de presiones, Presiones transitorias.

RESUMO

Oscrus pesados são considerados atualmente como uma classe de jazidas não convencional de maior interesse para a indústria petroleira. Alguns deles mostram um comportamento não Newtoniano pseudoplástico cujo modelo matemático difere do caso convencional e, portanto, os regimes de fluxo apresentam alguns comportamentos particulares. Os fluídos de faturamento, as espumas, alguns fluí-dos usados em recuperação melhorada e os lodos de perfuração, também caem nesta categoria. O fluxo esférico/hemisférico causado por completamento/penetração parcial merece um tratamento especial para fluxo pseudoplástico. Encontrou-se para este caso somente uma pesquisa na literatura que só introduz o modelo matemático.

Neste trabalho se estuda o comportamento da pressão e a derivada de pressão para fluxo esférico/hemisférico de um fluído ligeiramente compreensível, não Newtoniano lei de potência (pseudoplástico) e estendem-se a metodologias convencional e Tiab's Direct Synthesis (TDS) para propósitos interpretativos de provas de poços. Em fluxo esférico/hemisférico pseudoplástico, a pendente da curva da derivada já não é de -½, é mais muda com o valor do índice de comportamento de fluxo n, o que indica que a interpretação de dados de pressão para os sistemas em questão usando métodos tradicionais não seria exato. São introduzidas novas equações para estimar a permeabilidade esférica/hemisférica e o fator de dano esférico/hemisférico para tais sistemas. As equações foram verificadas satisfatoriamente com casos simulados.

Palavras chave: Fluído pseudoplástico, Consistência, Lei de potência, Fluxo radial, Completamento parcial, Penetração parcial, Análises de pressões, Pressões transitórias.

1. INTRODUCTION

A well with either partial penetration or partial completion causes the development hemispherical or spherical flow before the radial flow regime takes place. Spherical flow can occur in horizontal wells when its effective horizontal length is about 5 times shorter than the bed thickness.

Chatas (1966) presented the first discussion of unsteady-state spherical flow. Culham (1974) presented equations suitable for pressure buildup analysis but the wellbore storage distortion was not included. Later, Joseph and Koederitz (1985) presented analytical solutions including wellbore storage and damage skin effects. They conducted the interpretation via conventional analysis and type-curve matching. Proett and Chin (1998) introduced new more accurate analytical solutions and provided pressure and pressure derivative type-curve matching solution to the problem of spherical flow. Using the model proposed by Joseph and Koederitz (1985), Recently, Moncada et al. (2005) include the TDS technique, Tiab (1993), for well test interpretation of spherical and hemispherical flow in vertical oil and gas wells.

There have been some applications of well test analysis to Non-Newtonian fluids for interfase power-law non-Newtonian/Newtonian fluids, double porosity systems and even Bingham fluids by, respectively, Escobar, Martínez and Montealegre (2010), Escobar, Zambrano, Giraldo and Cantillo (2011) and Martinez, Escobar and Montealegre (2011). However, none of them considers either spherical or hemispherical flow. Actually, the unique work available for non-Newtonian spherical flow was presented by Ci-qun (1988) to only introduce the solution for infinite-spherical flow regime. He derived a nonlinear parabolic partial differential equation and provided asymptotic and approximate solutions of the linearized parabolic equation.

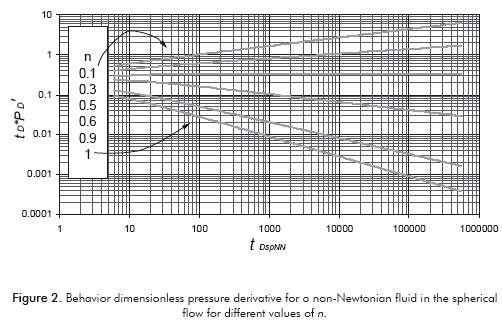
In this work, the solutions presented by Ci-qun (1988) were used to introduce the pressure behavior of transient spherical pseudoplastic. It is observed that the pressure derivative changes its slope from -½ (Newtonian case) to about 0.22 as the flow index varies from 1 to 0.1. Even, for n = 0.5 the pressure derivative becomes flat similar to radial Newtonian flow regime. Both the straight-line conventional method and the TDS technique were extended for well test interpretation.

The new equations were applied to simulated cases providing very low deviation errors with respect to the input simulation values. Since only one publication precedes this one, no field cases are presented, however, partial completion/penetration is everywhere and applicability of this work is valuable. Actually, our experience indicates that some wells with sand deposition easily develop hemispherical flow. If a well under these conditions is used for the injection of foams, fracturing fluids or tertiary recovery fluids and is then tested, the tools for interpretation are given here. This work is also very useful to understand the pressure and pressure derivative behavior of hemispherical/spherical non-Newtonian flow which is unknown until now. As observed in Figure 2, the pressure derivative displays a slope of -½ for the Newtonian case (n = 1) as expected. As the value of coefficient n decreases gradually until 0.1, the slope of the pressure derivative also increases gradually until a value of 0.22. An interesting fact occurs at an n value of 0.5 when the pressure derivative becomes flat which resembles the radial flow regime of a Newtonian fluid. This work also is very useful to understand the pressure and pressure derivative behavior of hemispherical/spherical non-Newtonian flow which was unknown until now.

2. MATHEMATICAL FORMULATION

Ci-qun (1988) presented a linearized form of the diffusivity equation for spherical non-Newtonian flow in porous media, as follows:

The Equation 1 in dimensionless form for transient spherical flow of Non-Newtonian power-law fluid is

The dimensionless initial and boundary conditions

He also presented the Laplace solutions for the case of infinite reservoir and constant-rate production. Notice that this equation becomes very particular according to the value of n. For n < 0.5 this is:

It is interesting to observe that for n = 0.5 Equation 6 reduces to the pseudo-radial flow case. It means that the pressure behavior of Non-Newtonian fluid in a spherical flow for n = 0.5 is the same as that of Newtonian fluid in radial flow.

For 0.5 < n≤ 1:

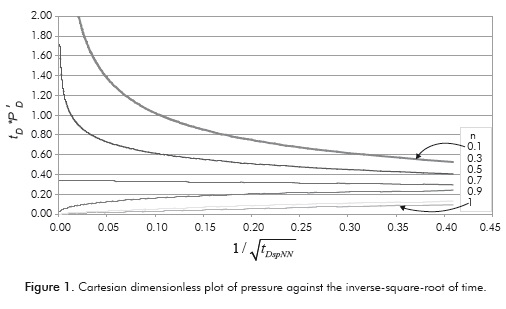
When n = 1, Equation 6 reduces to the spherical flow case of Newtonian fluids. The results of the simulations are reported in Figures 1 and 2. In conventional crude and gas, a plot of pressure versus the inverted value of the square root of time provides a straight line which slope and intercept are used to estimate the spherical (tridimensional) permeability and the spherical skin factor. Observe in Figure 1 that as n decreases its value the straight-line disappears and become more curved at later times. This means that the conventional analysis for Newtonian fluids should not be applied for non-Newtonian case. On the other hand, the pressure derivative, Figure 2, increases its slope from -½ to about 0.22 as n goes from 1 to 0.1. On one hand, for the Newtonian case, n = 1, the pressure derivative displays a slope of -½ as expected which validates the solution presented by Ci-qun (1988). On the other hand, the pressure derivative becomes flat (radial flow) for n=0.5. Therefore, new Equations for handling values of n less than one will be developed later on in this paper.

3. FUNDAMENTAL EQUATIONS

The dimensionless pressure, P_D, and the dimension-less time, t_D, for spherical and radial symmetry are:

Where:

And,

4. INTERPRETATION METHODOLOGIES

Conventional Analysis

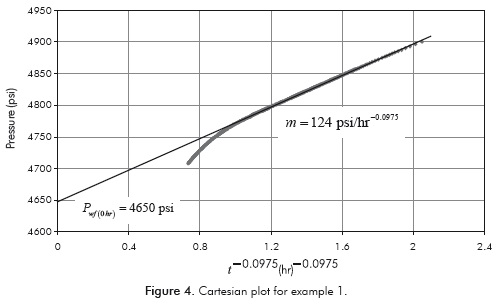
As seen in Figure 1, the Cartesian plot of P versus 1/t⁰-⁵ only works for n = 1. Therefore, a plot of pressure versus t^β is required; being β the slope of the Cartesian plot which depends upon the value of n.

1) The Cartesian spherical flow slope for a non-Newtonian fluid is given by:

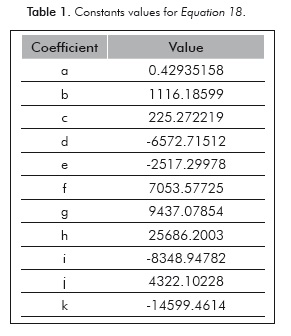
With a R² = 0.99999977. The values of the coefficients are given in Table 1.

Which involves a correction factor given by:

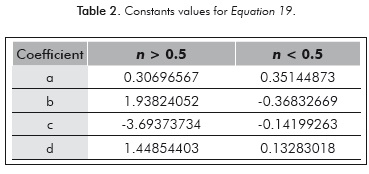
The values of coefficients are presented in Table 2.

2) The dimensionless pressure for spherical flow in a non-Newtonian fluid is expressed according to the value of n:

For n # 0.5 y n ≤ 1:

Replacing the dimensionless quantities given by Equations 9 and 11 into Equation 20 yields:

As indicated before, notice that Equation 21 suggests that a Cartesian plot of P_wf vs. t^β gives a linear trend which slope and intercept allow for the estimation of the spherical permeability and spherical skin factor, such as:

For buildup pressure tests a plot of P_WJ vs. (tp+Dt)β-(tp)β ought to be built instead. Equations 22 and 23 are used for similar purposes.

Ifβ>0.5, the slope is taken as positive and if β < 0.5, the slope is taken as negative.

For n = 0.5, the governing equation is given by:

Replacing the dimensionless quantities given by Equations 9 and 12 into Equation 25, we obtain:

Equation 26 suggests that a semilog plot of P vs. tβ or P_wftβ gives a linear trend which slope and intercept allow for the estimation of the spherical permeability and spherical skin factor, such as:

TDS Technique

Several characteristic behaviors are chosen from the pressure and pressure derivative log-log plot, as follows:

1) Replacing the dimensionless quantities given by Equations 10 and 11 into Equation A.1 will result:

Replacing the dimensionless quantity given by Equation 10 into Equation A.2 allows obtaining:

2) The spherical skin factor for a non-Newtonian fluid is derived from the ratio of the dimensionless pressure equation by the dimensionless pressure derivative equation and solving for S_spNN.

For n # 0.5 and n< 1 using Equations 20 and A.1 gives:

For n = 0.5 using Equations 24 and A.2 also gives:

3) Replacing the dimensionless quantities given by Equations 14 and 15 in Equation A.11 provides an expression to estimate reservoir permeability:

An erroneous version of the dimensionless pressure and skin factor were presented by Martínez, Escobar and Cantillo (2011) and Escobar et al. (2010). The corrected version for skin factor, which is invalid for n = 1 is:

4) The line corresponding to the spherical flow and the late radial flow line of the dimensionless pressure derivative in radial symmetry intersect according to:

Then, for n # 0.5 and n< 1, the intercept oí Equations A.8 with Equation A.11 gives:

Replacing the dimensionless time and solving for the time of intersection will result in:

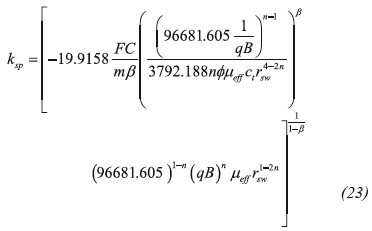
From which spherical permeability can be solved to obtain:

For n = 0.5, the intercept of Equation A.9 and A.11 yields:

After replacing the dimensionless time and solving for time of intersection will give:

Also solving for the spherical permeability allows obtaining:

This work did not considered wellbore storage effects. However, if given the case, the wellbore storage coefficient can be estimated using the same expression for the Newtonian fluids as presented in Equation 8 by Katime-Meindl and Tiab (2001):

As, it is well known, using the coordinates of a point in the early unit-slope region is used to estimate the wellbore storage coefficient.

5. EXAMPLES

Example 1

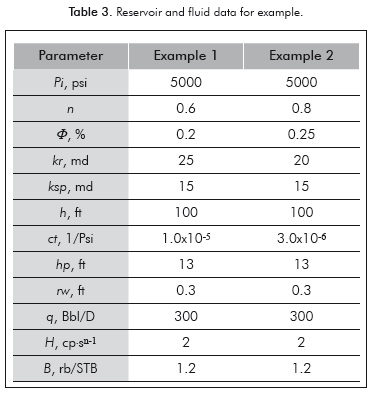
A synthetic pressure test of a well inside an infinite reservoir was generated with the data in Table 3. Use both TDS technique and conventional analysis to obtain permeability and spherical skin factor.

Solution

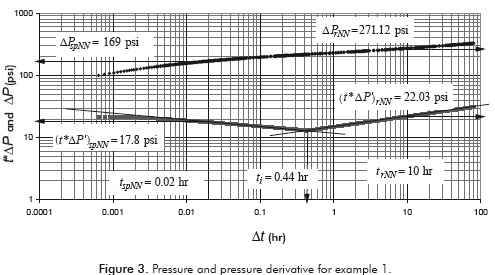
The log-log plot of pressure and pressure derivative against time is given in Figure 3. From that plot the following information was read:

First, an α value of 0.16667 is evaluated using an expression introduced by Escobar et al. (2010).

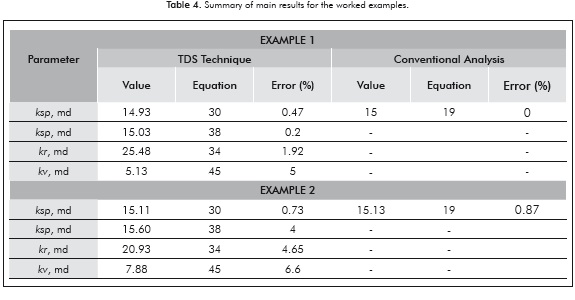
Equation 17 provides a value of µ_eff = 0.00491 cp(s/ ft)^n-1. Then, a radial permeability of 25.48 md is estimated with Equation 34 and a spherical permeability of 14.93 md is obtained with Equation 30. G₂ = 5.183 hr/ft^3-n is calculated with Equation 16 and a value of s_rNN of 38.83 is found using Equation 35.

Now, Equation 18 is to find a slope value of -0.0975 and Equation 19 is used to find a correction factor 1.573. The spherical permeability is again estimated using Equation 30. The equivalent wellbore radius is found to be 1.725 ft using an expression introduced by Chatas (1966):

A spherical skin factor of 4 is found with Equation 32 and a vertical permeability of 5.13 md is estimated with Equation 45.

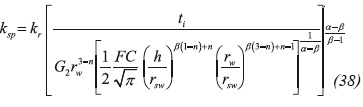
The spherical permeability is calculated again with Equation 38. It results to be 15.03 md.

Regarding the conventional method, Figure 4 shows a Cartesian plot of P versus t ^-0.0975 which slope provides a spherical permeability of 15 md by means of Equation 23 and a spherical skin factor of 4 with Equation 24. Main results are given in table 4 for comparison purposes.

Example 2

Another synthetic pressure test for a well in an infinite reservoir was generated with information from Table 3. Perform the same characterization of example 1.

Solution

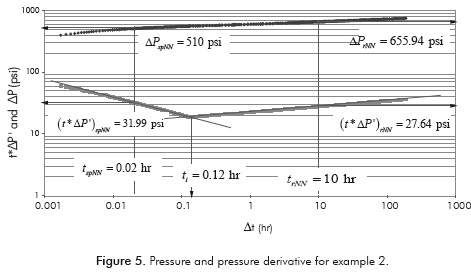
The log-log plot of pressure and pressure derivative against injection time is given in Figure 5. From that plot the following information was read:

As for the former example, an a value of 0.0909 is calculated with Equation 43 and the non-Newtonian radial permeability of 20.93 is estimated with Equation 34. A µ_eff value of 0.0996 cp(s/ft)^n-1 is found with Equation 17 and a G₂ = 8.324x10^-5 hr/ft³-n is calculated with Equation 16.

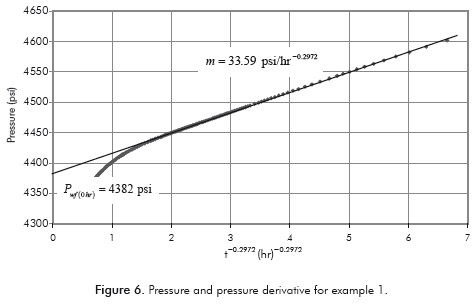
Equation 35 allows to obtain a spherical skin factor of 23.45. Equations 18 and 19 are used to obtain values of 0.2972 and 1.265 for slope and corrections factor, respectively. The apparent wellbore radius is equal to example 1.

Spherical permeability is calculated with Equation 30. Its value is 15.11 md.

Values of 0.67 and 7.88 md are found for spherical skin factor and vertical permeability, respectively, using Equations 32 and 45. Finally, a spherical permeability of 15.6 md is found with Equation 38.

The values of slope and intercept from the Cartesian plot shown in Figure 6 allows for the calculation of a spherical permeability of 15.13 md and skin factor of 0.674 using Equations 23 and 24, respectively. The main results for this exercise are also provided in Table 4.

6. DISCUSSION

Very low errors in the estimation of spherical permeability and radial permeability were found in all of the worked synthetic examples. Actually, for the presented examples the errors are lower than 4% for the spherical permeability and 7% for radial permeability as shown in Table 4. However, we believe that this is function of how well the interpreter reads the characteristic points for which purpose computer applications are recommended. This demonstrates that the developed expressions are accurate and can be trustily applied with any of the two provided methodologies presented in this work.

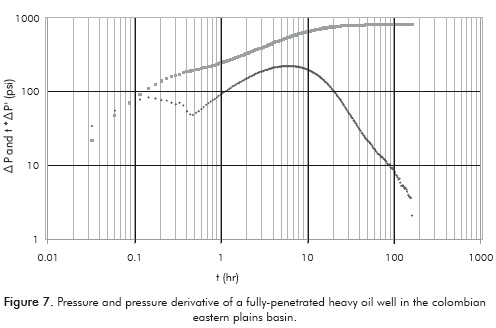
Even though, the worked examples are presented for synthetic cases, this work is considered to have a great potential in heavy oil fields in which bottom water influxes exist as the example provided in Figure 7 in which the pressure derivative goes down due to the aquifer influence. This leads to avoid the radial flow to be seen. For such cases is recommended to complete the well as partially penetrated to delay the influence of the aquifer and conduct a well test using a bottom-hole shut-in device so the hemispherical flow can be seen and analyzed.

7. CONCLUSIONS

• New expressions were introduced to estimate permeability and the skin factor for spherical fow in non-Newtonian fuids pseudoplastic fuid using both the TDS and straight-line conventional techniques. The presented Equations were successfully applied to synthetic cases providing acceptable margin of errors.
• Corrected expressions for the dimensionless pressure and mechanical skin factor (radial fow regime) for non-Newtonian fuid were introduced.

8. RECOMMENDATIONS FOR FUTURE WORK

This work is based upon the only one on the subject presented by Ci-qun (1988). Ci-qun's solution did consider neither skin nor wellbore storage effects. However, spherical/hemispherical skin factor expressions were included with the help of the development of approximate governing pressure Equations. Notice that both TDS and straight-line conventional analyses are introduced in this paper for characterizing both partial penetration or partial completion by well test analysis. Needless to say that the conventional analysis works perfectly as long as the flow regimes are well defined which may be supported on the pressure derivative curve. Thereby, a type-curve methodology needs an exact analytical solution handling both skin and wellbore storage which does not exist so far. It is recommended to generate the above mentioned solution to generate a type-curve matching methodology for the problem dealt with in this work. The analytical solution will also serve to study wellbore storage, skin effects and length of the completion interval on masking the spherical/hemispherical flow regime.

ACKNOWLEDGMENTS

The authors gratefully thank Universidad Surcolombiana for providing support to the completion of this work.

REFERENCES

Chatas, A.T. (1966). Unsteady spherical flow in petroleum reservoirs. SPE Journal, 6(2), 102-114        [ Links ]

Ci-qun, L. (1988). Transient spherical flow of non-newtonian power-law fluids in porous media. Applied Mathematics and Mechanics, 9(6), 521-525.         [ Links ]

Culham, W.E. (1974). Pressure buildup Equations for spherical flow regime problems. SPE Journal, 14(6), 545-555.         [ Links ]

Escobar, F. H., Martínez, J. A. & Montealegre-M., M. (2010). Pressure and pressure derivative analysis for a well in a radial composite reservoir with a non-newtonian/newtonian interface. CT&F-Ciencia, Tecnología y Futuro, 4(2), 33-42.         [ Links ]

Escobar, F.H., Zambrano, A.P, Giraldo, D.V. & Cantillo, J.H. (2011). Pressure and pressure derivative analysis for non-newtonian pseudoplastic fluids in double-porosity formations. CT&F-Ciencia, Tecnología y Futuro, 4(3), 47-59.         [ Links ]

Joseph, J.A. & Koederitz, L.F. (1985). Unsteady-state spherical flow with storage and skin. SPE Journal, 25(6), 804-822.         [ Links ]

Katime-Meindl, I. & Tiab, D. (2001). Analysis of pressure transient test of non-newtonian fluids in infinite reservoir and in the presence of a single linear boundary by the direct synthesis technique. SPE Annual Technical Conference and Exhibition. New Orleans, Louisiana. SPE 71587.         [ Links ]

Martínez, J.A., Escobar, F.H. & Cantillo, J.H. (2011). Application f the TDS technique to dilatant non-newtonian/ newtonian fluid composite reservoirs. Ingeniería e Investigación, 31(3), 130-134.         [ Links ]

Martínez, J.A., Escobar, F.H. & Montealegre-M., M. (2011). Vertical well pressure and pressure derivative analysis for Bingham fluids in a homogeneous reservoirs. Dyna, 78(166), 21-28.         [ Links ]

Moncada, K., Tiab, D., Escobar, F.H., Montealegre-M, M., Chacon, A., Zamora, R.A. & Nese, S.L. (2005). Determination of vertical and horizontal permeabilities for vertical oil and gas wells with partial completion and partial penetration using pressure and pressure derivative plots without type-curve matching. CT&F-Ciencia, Tecnología y Futuro, 3(1), 77-95.         [ Links ]

Proett, M.A. & Chin, W.C. (1998). New exact spherical flow solution with storage for early-time test interpretation with applications to early-evaluation drillstem and wireline formation testing. SPE Permian Basin Oil and Gas Recovery Conference. Midland, Texas, SPE 39768.         [ Links ]

Tiab, D. (1993). Analysis of pressure and pressure derivative without type-curve matching: 1- Skin and wellbore storage. Journal of Petroleum Science and Engineering, 12(3), 171-181.         [ Links ]