Ecuación del movimiento de un elemento finito lineal plano elástico dinámico con ocho grados de libertad

Equação do movimento de um elemento finito plano elástico dinâmico com oito graus de liberdade

Motion equation of a finite dynamic elastic plane lineal element with eight degrees of freedom

Américo G. Hossne¹

1 PhD, americohossne@cantv.net, Universidad de Oriente, Núcleo de Monagas, Maturín- Venezuela

(Recepción: 02-oct-2009. Modificación: 21-may-2010. Aceptación: 20-ago-2010)

---

Resumen

Un elemento finito lineal con sección transversal constante puede adoptar cualquier orientación en el plano y sus extremos o nodos lo ligan al resto de los elementos. La energía cinética (T) y potencial (V) de un elemento elástico dinámico son el basamento en la implementación del principio de Hamilton para la definición de un elemento finito. La definición de la energía cinética y potencial es el primer paso para la formulación variacional preliminar a la enunciación por elementos finitos que se utiliza para resolver, dígase, los problemas de mecanismos que se mueven en el plano utilizando la ecuación de Hamilton. El objetivo general consistió en definir la ecuación del movimiento de un elemento finito lineal plano elástico dinámico utilizando la ecuación de Hamilton, a partir de la lagrangiana (T-V) obtenida con el uso de un polinomio de quinto y uno de primer grados, con ocho grados de libertad, cuatro en cada nodo, que representaron las deformaciones: axial (u(x)), transversal (w(x)), pendiente ((dw(x)/dx)) y curvatura ((d²w(x)/dx²)). La deformación debido al cizalleo transversal, insignificante comparado con la deformación flexional y la axial, la inercia rotatoria y las fuerzas friccionales en las uniones, fueron desestimadas con el fin de producir un elemento amigo. Los objetivos específicos fueron producir: (a) la matriz de masa de traslación [M_D], (b) la matriz giroscópica de traslación [A_D], (c) la matriz de rigidez total de traslación [K_D], y (d) el vector de deformación (S). Como resultado se forjó la ecuación del movimiento de un elemento finito lineal plano elástico dinámico

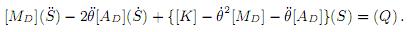
Se concluyó que la ecuación obtenida variacionalmente con la aplicación del principio de Hamilton es un modelo cuyo procedimiento puede ser utilizado cuando se requiera aumentar el número de grados de libertad del modelo.

Palabras claves: principio de Hamilton, elemento finito lineal plano elástico dinámico, mecanismos elásticos de cuatro barras, lagrangiana, matriz de masas, matriz de rigideces y matriz giroscópica.

---

Resumo

Um elemento finito linear com seção atravessada constante, pode adotar qualquer orientação em seu plano, e seus extremos os ligam aos restos dos elementos. A energía cinética (T) e potencial (V) de um elemento elástico dinâmico é o só é baseado do princípio de Hamilton para a definição de um elemento finito. A definição da energia cinética e potencial é o primeiro passo para a formulação variacional preliminar para a enunciação para elementos finitos que é usado para resolver, diga, os problemas de mecanismos que se mudam o usando plano a equação de Hamilton. O objetivo geral consistiu em definir a equação de movimento de um elemento plano elástico dinâmico linear finito que usa a equação de Hamilton a partir da grangiana (T − V) por meio de um quinto e primeiro polinômios de grau, com oito graus de liberdade, quatro em cada nodo que representou as deformações: axial (u(x)), atravesse (w(x)), rampa ((dw(x)/dx)) e dobra ((d²w(x)/dx²)). A deformação devido a tosquiar através, insignificante com respeito a flexional e deformações axiais, a inércia rotatória e as forças friccionais nos nodos, foram desestimadas com o fim da produção de um elemento amigável. Os objetivos específicos eram acontecer: (a) a matriz de mesma translação [M_D], (b) a matriz giroscópia de translação [A_D], (c) a matriz de rigidez total de translação [K_D], y (d) o vetor de deformação (S). Como resultado se forjou a equação do movimento d eum elemento finito linear plano elástico dinâmico

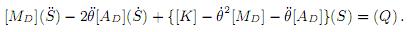
Se concluiu que a equação aplicável, cujo procedimento pode ser utilizado quando se requer aumentar o número de graus de liberdade.

Palavras chaves: principio de Hamilton, elemento finito lineal plano elástico dinâmico, mecanismos elásticos de quatro barras, grangiana, matriz de massas, matriz de rigidez e matriz giroscópica.

---

Abstract

A lineal finite element with constant traverse section, it can adopt any orientation in the plane, and their ends or nodes tie it to the rest of the elements. The kinetic energy (T) and potential (V) of a dynamic elastic element are the basement in the implementation of the Hamilton principle for the definition of a finite element. The definition of the kinetic energy and potential is the first step for the preliminary variational formulation to the enunciation for finite elements that it is used to solve, say, the problems of mechanisms that move in the plane using the Hamilton equation. The general objective consisted on defining the equation of the movement of a finite lineal dynamic elastic plane element using the equation of Hamilton, starting from the lagrangiana (T − V) obtained with the use of a polynomial of fifth and first degree, with eight degrees of freedom, four in each node that represented the deformations: axial (u(x)), traverse (w(x)), slope ((dw(x)/dx)) and bend ((d²w(x)/dx²)). The deformation due to traverse shearing, insignificant with respect to flexional and axial deformations, the rotational inertia and the frictional forces in the nodes, were underrated with the purpose of producing a friendly element. The specific objectives were to take place: (a) the translational mass matrix [M_D], (b) the translational gyroscopic matrix [A_D], (c) the translational total rigidity matrix [K_D], and (d) the deformation vector (S). As a result the movement equation of a finite lineal dynamic elastic plane element was forged

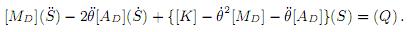
On concluded that the equation obtained variationally with the application of the Hamilton Principle is the state-of-the-art pattern, and that the procedure can be used when it is required to increase the number of the pattern freedom degrees.

Key words: Hamilton principle, elastic dynamic planar element, four bar planar mechanism, lagrangian, mass matrix, rigid matrix and gyroscopic matrix.

 

---

1 Introducción

Este método constituye un método numérico destinado a resolver, mediante ecuaciones matriciales, las ecuaciones diferenciales que se plantean en sistemas discretos. En el caso de sistemas continuos, el método consiste en discretizar el dominio de interés en elementos finitos y resolver, mediante un funcional de prueba o de aproximación, la ecuación que rige el sistema en cada elemento finito para luego sumar todas las soluciones. El método de elemento finito es un método numérico que surgió como tal en los años sesenta [1]. El método fue propuesto en 1943, pero no fue hasta 1956 que se presentaron los primeros resultados, y en 1960 se le llamó método de elemento finito [2]. A partir de la aparición del método del elemento finito en 1956, se utilizó la idea de aproximar a las funciones a través de subregiones en que se divide la región original previamente seleccionadas, denominadas elementos finitos. El concepto básico de este método es el de dividir el continuo en un número finito de elementos, es decir, discretizar el continuo y resolver sobre cada uno de los elementos las ecuaciones del sistema para después ensamblar la solución total[3]. Turner (1956), FR obtuvo las matrices de rigidez (armaduras y vigas). Clough (1960) FR fue el primero en utilizar el término elementos finitos. En 1970 se crean las bases formales del método.

El cálculo variacional es un área de la matemática clásica con aplicación en las ciencias e ingeniería. Los primeros trabajos sobre el cálculo variacional fueron un intento para extender los conceptos de Newton y Leibniz al problema de encontrar un mínimo de un funcional. Se observó que muchas de las leyes que gobiernan el fenómeno de la naturaleza emanan del principio de un recorrido mínimo de tiempo entre dos puntos. El principio de Hamilton (1805-1865) es uno de esos principios, el cual es considerado el punto de partida de los acercamientos variacionales de mecánica y establece la unión entre las matemáticas del cálculo variacional y la física de los sistemas naturales. El análisis y diseño de mecanismos con eslabones elásticos han sido investigados por variadas metodologías. Los autores de [4] utilizaron el principio de Hamilton con aplicación de la ecuación de Reissner [5] para obtener un elemento finito basado en deformaciones para el análisis dinámico de elementos elásticos planos. En [6, 7, 8, 9, 10, 11, 12, 13, 14] utilizaron tanto el método de fuerzas como el método de desplazamiento en la teoría de elementos finito para el análisis de estructuras y para modelar eslabones elásticos. El método por el acercamiento de los parámetros indicadores también fue utilizado mostrando ser un método útil [15]. En [16] describieron, por un acercamiento general, la derivación de la ecuación del movimiento de un mecanismo plano a altas velocidades; los autores se basaron en el trabajo de muchos investigadores y el método de elemento finito para desarrollar las matrices de masas y rigideces con la aplicación de la ecuación de Lagrange en un eslabón elástico con seis grados de libertad, tres por nodos representando la deformación de cada nodo: deformación axial, deformación transversal y rotación; utilizaron un polinomio de primer grado para la deformación axial y uno cúbico para describir la flexión y el desplazamiento transversal.

En la síntesis de mecanismos flexibles, en orden histórico, están los trabajos de Avilés, [10, 17, 18, 19]. Ellos generaron ecuaciones globales de mecanismos con miembros axialmente rígidos. El procedimiento fue ilustrado al emplear un mecanismo plano de cuatro barras con un elemento por barra; en el proceso algebraico utilizaron un polinomio de quinto grado para un total de tres grados de libertad por nodo: deformación transversal, pendiente o rotación y curvatura; generándose una matriz de 7×7 al considerar la deformación axial constante. Saggere y Kota [20] emplearon, en su modelo, polinomios de segundo y tercer grado para un elemento cortante para la síntesis de mecanismos con uniones flexibles o de segmentos flexibles relativamente largos aplicados a mecanismos de cuatro barras.

En este trabajo se consideraron cuatro grados de libertad por nodo con el uso de un polinomio de quinto grado y uno de primer grado, lo cual produjo matrices de 8 × 8 que, con uso del mismo procedimiento, podrían introducir más variables. Se desestimaron la deformación por cortante, inercia rotatoria y las fuerzas friccionales. Los objetivos fueron: (a) presentar, a partir de la energía cinética y potencial de un elemento plano elástico dinámico, por aplicación de la ecuación de William Hamilton, con técnicas de elemento finito, una ecuación de movimiento de un elemento finito lineal dinámico elástico con ocho grados de libertad conformados por dos polinomios, uno de quinto grado para representar las deformaciones transversales y uno de primer grado para representar las deformaciones axiales y (b) ilustrar el procedimiento de aplicación en un mecanismo de cuatro barras con uno y dos elementos por barra.

2 Metodología

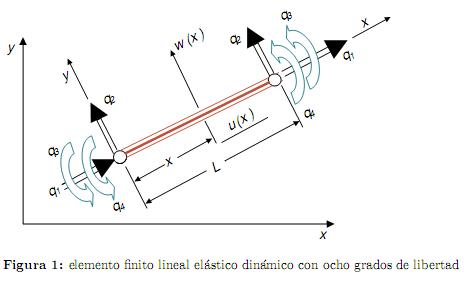
La figura 1 muestra la idealización del elemento finito lineal elástico dinámico utilizado, en donde q₁, q₂, q₃ y q₄ representan las deformaciones axial (u(x)), transversal (w(x)), pendiente ((dw(x)/dx)) y curvatura ((d₂w(x)/dx₂)), respectivamente.

El problema variacional fue expuesto por lo que es conocido en mecánica clásica como el principio de Hamilton. El sistema fue considerado conservador,

es decir, cada fuerza que actúa es derivable de un potencial. Permítase a T representar la energía cinética total y V la energía potencial. La lagrangiana LF = (T - V) de un elemento finito plano elástico dinámico con ocho grados de libertad fue definido por [21]. Los métodos variacionales transforman el problema de integración de una ecuación diferencial por el de calcular el valor extremal de un funcional. El funcional de la ecuación diferencial se construye de tal manera que al sustituir la función solución de la ecuación diferencial se obtiene un valor extremal. El principio de William R. Hamilton por el cálculo variacional [4, 22, 23] establece que el movimiento actual que conecta dos estados del sistema, dígase en tiempo t₁ y t₂, es el que minimiza la integral

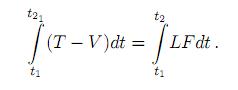
El tipo general de la lagrangiana tiene la forma de

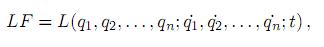
tiene un extremal

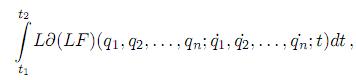
en donde ∂(LF) denota la variación en LF de su valor en el movimiento actual en el instante t a su valor en el mismo instante en el camino recorrido. Del trabajo de [21] se conoce a T y a V, entonces LF se obtiene por diferencia igual a

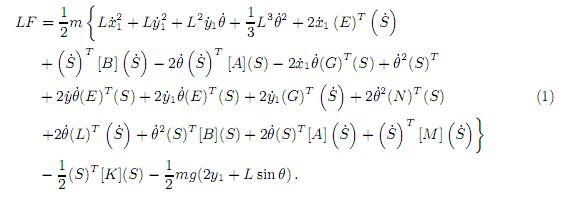
Para poder aplicar el principio de Hamilton se tomó variación (δ) a (1) con respecto a la deformacion (S), ecuación (9), obteniéndose

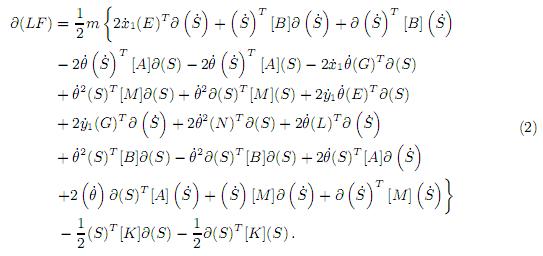
Al sumar términos iguales y arreglo en (2), se obtuvo

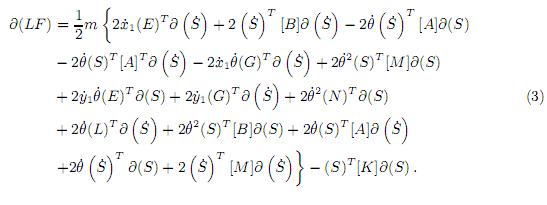
Para poder aplicar el principio de Hamilton, los términos de (3) con las variaciones del tipo ∂ (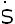) tuvieron que ser transformados a ∂(S). Para lograrlo se aplicó integración por partes [24, 25]; utilizando (4)

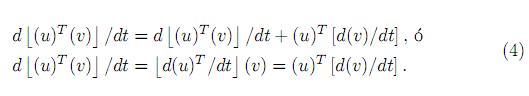
Que por integración se obtiene

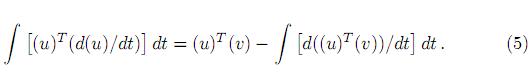
Se realizaron un total de siete trasformaciones, que no se añadieron, con (5) a los términos de (3) con ∂ (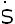), transformándolos a ∂(S). Luego, aplicando el principio de Hamilton se obtuvo:

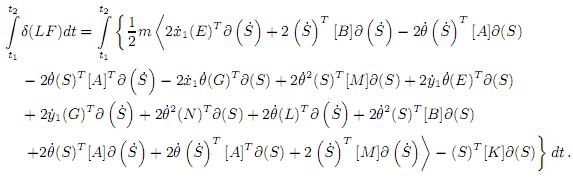
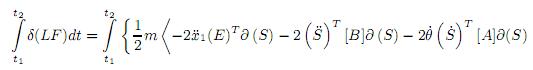
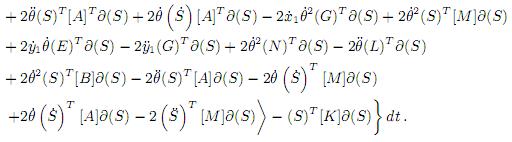
Ordenando

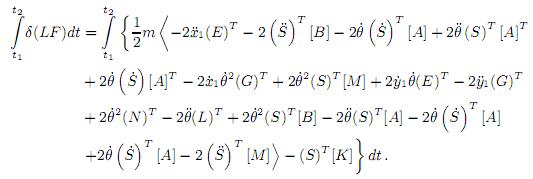
Aplicando la integral de Hamilton

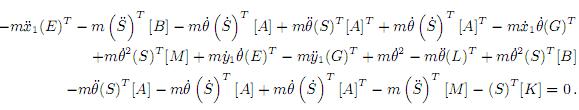
Primer ordenamiento

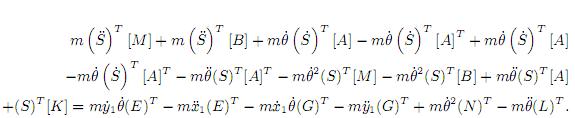
Segundo ordenamiento

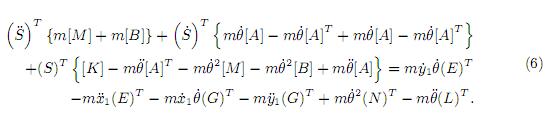
En el proceso matemático las transformaciones se hicieron considerando que las deformaciones son pequeñas y los cambios a coordenadas globales se llevaron a cabo, utilizando la matriz

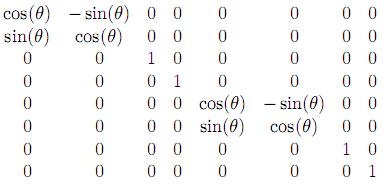
3 Resultados y discusiones

Introduciendo en (6) las substituciones:

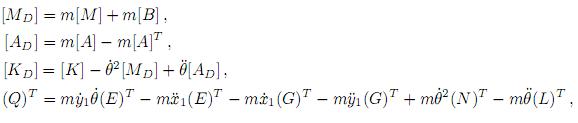
resultó

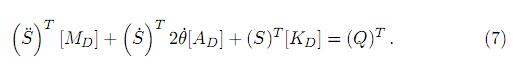
Finalmente, tomando transpuesta en (7), se forjó la ecuación del movimiento de un elemento finito lineal plano elástico dinámico

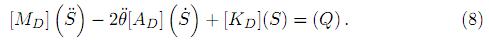
Al reemplazar 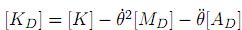en (8), se obtuvo

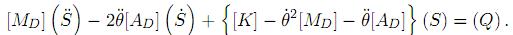
La matriz [M_D], anexo 5, se le definió como la matriz de masa de traslación; la matriz [A_D], anexo 5, como la matriz giroscópica de traslación; la matriz [K_D], anexo 5, como la matriz de rigidez total de traslación; y el vector (S), ver (9), representa el vector deformación. En el modelo presentado por[19] utilizaron un polinomio de quinto grado para un total de tres grados de libertad por nodo: deformación transversal, pendiente o rotación y curvatura; generándose una matriz de 6 × 6, y al introducir como constante la deformación axial generaron matrices de 7 × 7. El avance de este trabajo consistió en introducir la deformación axial como variable y para ello se utilizaron dos polinomios: uno de quinto grado para representar las deformaciones transversales y uno de primer grado para representar las deformaciones axiales, que generaron matrices de 8 × 8. Este procedimiento permitiría introducir otras variables al utilizar mayores o más polinomios.

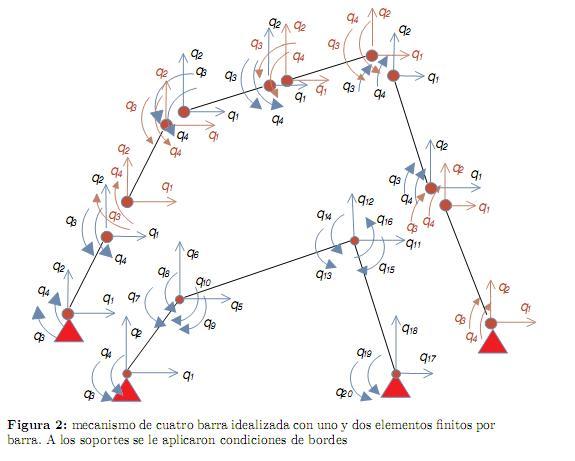
Por ejemplo, en la aplicación del elemento definido, la figura 2 muestra un mecanismo de cuatro barras idealizado con uno y dos elementos por barra. Un total de 20 y 48 incógnitas. Al mecanismo de dos elementos por eslabón se reducirían las incógnitas al aplicar las condiciones de bordes.

4 Conclusiones

Por vía geométrica y algebraica, a partir de la energía cinética y potencial producto de dos polinomios representando ocho grados de libertad, se definió variacionalmente, con la aplicación del principio de Hamilton, la ecuación de movimiento de un elemento finito lineal plano elástico dinámico. El modelo podría ser aplicado considerando uno o más elementos por eslabones de un mecanismo.

Con la metodología utilizada se podrían definir modelos con un mayor número de grados de libertad, representando así otras deformaciones y con la posibilidad de definir un elemento espacial para el análisis de mecanismos en tres dimensiones.

5 Anexos

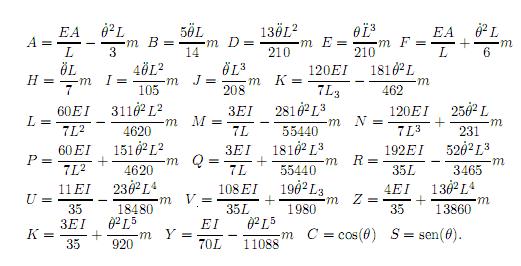
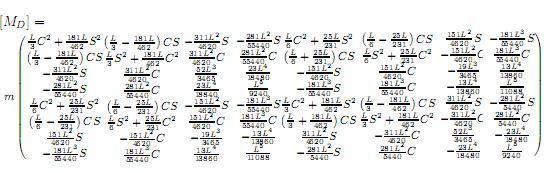
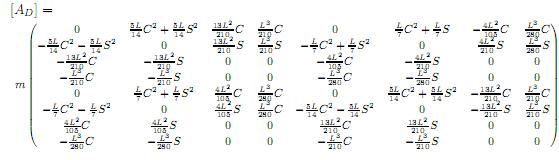
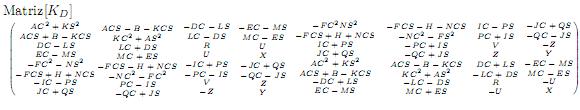
Referencias

1. KH. Huebner, EA. Thornton, TG. Byrom. The finite element method for engineers, 3rd Edition, ISBN 0471547425. John Wiley, 1995. Referenciado en 68         [ Links ]

2. S. Kobayashi, S-I Oh, T. Altan. Metal forming and the finite element method, ISBN 0195044029. Oxford University Press, 1989. Referenciado en 68         [ Links ]

3. SV. Patankar. Numerical heat transfer and fuid flow. ISBN 0891165223, Taylor & Francis, 1980. Referenciado en 68         [ Links ]

4. M. Gams, M. Saje, I. Srpeie, I. Planinc. Strain-base finite element for the dynamic analysis of elastic planar beams, http://www.scix.net/Files/aceptedpapers/Accepted/Gams.pdf, University of Ljubljana, Faculty of Civil and Geodetic Engineering, SI-1115 Ljubljana, Jamova 2, Slovenia, 2007. Referenciado en 68, 70         [ Links ]

5. E. Reissner. On one-dimensional finite-strain beam theory: the plane problem. Journal of Applied Mathematics and Physics (ZAMP), 23(5), 795-804 (1972). Referenciado en 68         [ Links ]

6. A. Midha. Dynamics of high speed linkages with elastic members. Doctoral dissertation, University of Minnesota, Minnesota, 1977. Referenciado en 68         [ Links ]

7. A. Midha, AG. Erdman, GN. Sandor, AG. Frohrib. An alternate computationally efficient and conservative method for kineto-elastodynamic analysis of mechanisms. Proc. 4th OSU appl. Mech. Conf. Chicago, Illinois, (1975). Referenciado en 68         [ Links ]

8. R. M. Alexander and K. L. Lawrence. An experimental investigation of the dynamic response of an elastic mechanism. Journal of Engineering for Industry, ISSN 0022-1817, 96(1), 268-274 (1974). Referenciado en 68        [ Links ]

9. U. Oktay. Finite element method-basic concepts and applications. Intext Educational Publishers, New York, 1973. Referenciado en 68         [ Links ]

10. IA. Iman. General method for kineto-elastodynamic analysis and design of high speed mechanisms. Doctoral dissertation, Rensselaer Polytechnic Institute, New York, 1973. Referenciado en 68, 69         [ Links ]

11. AG. Erdman. A general method for kineto-elastodynamic analysis and synthesis of mechanisms. Doctoral dissertation, Rensselaer Polytechnic Institute, New York, 1972. Referenciado en 68         [ Links ]

12. RC. Winfrey. Dynamics of mechanisms with elastic links. Doctor dissertation, UCLA, 1969. Referenciado en 68         [ Links ]

13. JS. Przemieniecki. Theory of matrix structural analysis. ISBN 0070509042. McGraw-Hill, New York, 1968. Referenciado en 68         [ Links ]

14. CH. Walter and F. R. Moshe. Dynamics of structures. ISBN 013222075X. Prentice-Hal, Englewood cliffs, New Jersey, 1964. Referenciado en 68         [ Links ]

15. JP. Sadler. A lumped parameter approach to kineto-elastodynamic analysis of mechanisms. Doctoral dissertation, Rensselaer Polytechnic Institute, New York, 1972. Referenciado en 68         [ Links ]

16. A. Midha, AG. Erdman, DA. Frohrib. Finite element approach to mathematical modeling of high-speed elastic linkages. Mechanism and Machine Theory, ISSN 0094-114X, 13(6), 603-618 (1978). Referenciado en 68         [ Links ]

17. R. Avilés, G. Ajuria, V. Gómez-Garay, S. Navalpotro. Comparison among nonlinear optimization methods for the static equilibrium analysis of multibody systems with rigid and elastic elements. Mechanisms and Machine Theory, ISSN 0094-114X, 35(8), 1151-1168 (2000). Referenciado en 69         [ Links ]

18. ZE. Boutaghou, AG. Erdman. A design methodology for system parameters synthesis of elastic planar linkages. Journal of Mechanical Design, ISSN 1050- 0472, 114(4), 542-546 (1993). 69         [ Links ]

19. WL. Cleghorn, RG. Fenton, B. Tabarrock. Optimum design of high-speed flexible mechanismsCalcul optimum de mecanismes flexibles de grande vitesse. Mechanisms and Machine Theory, ISSN 0094-114X, 16(4), 394-406 (1981). Referenciado en 69, 75        [ Links ]

20. L. Saggere, S. Kota. Synthesis of Planar, compliant four-bar mechanisms for compliant-segment motion generation. Journal of Mechanical Design, ISSN 1050-0472, 123(4), 535-541 (2001). Referenciado en 69        [ Links ]

21. AJ. Hossne. Lagrangiano de un elemento finito plano elástico dinámico con ocho grados de libertad. Ingeniería, ISSN 1665-529X, 11(1), 25-36 (2007). Referenciado en 70, 71         [ Links ]

22. D. Bel, M. Doblaré. Formulación de elementos finitos Lagrangianos y Hamiltonianos Bond-Graph para la simulación dinámica de sistemas multidisciplinares. Universidad de Zaragoza, IV Congreso de Métodos Numéricos en Ingeniería. Sevilla, 1-21 (1999). Referenciado en 70         [ Links ]

23. Dare A. Wells. Schaum's Outline of Lagrangian Dynamics: With a Treatment of Euler's Equations of Motion, Hamilton's Equations and Hamilton's Principle, ISBN 978-0070692589, Schaum's Outline, 1967. Referenciado en 70        [ Links ]

24. O. Brüls, G. Kerschen. Flexible multibody systems with finite elements. ULg-Department of Aerospace and Mechanical, 1-55 (2007). Referenciado en 72         [ Links ]

25. E. Bänsch, L. Tobiska, N. Walkington. Mini-Workshop: Interface problems in Computational fluid dynamics. Mathematisches Forschungsinstitut Oberwolfach, 2(1), 465-502 (2005). Referenciado en 72        [ Links ]