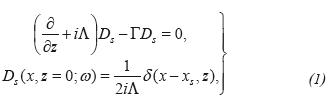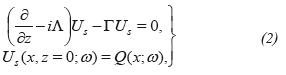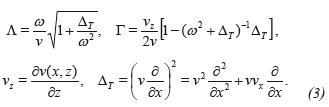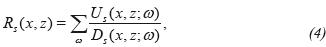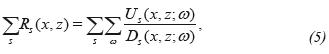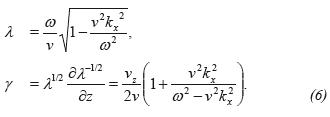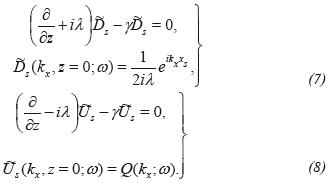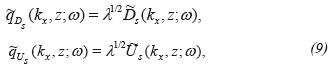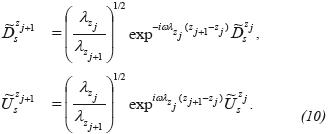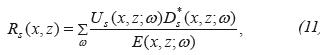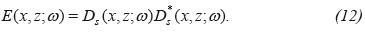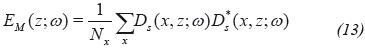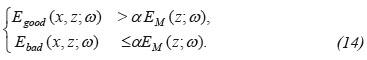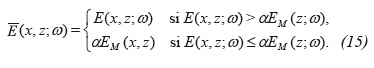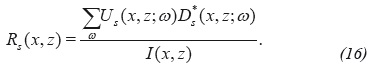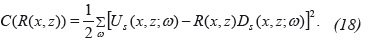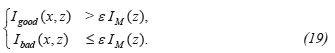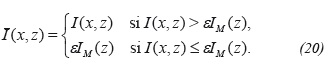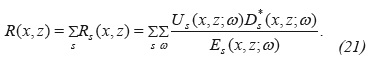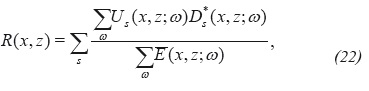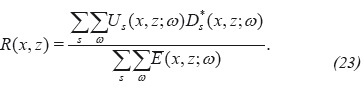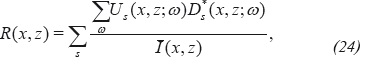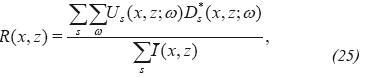DECONVOLUTION-TYPE IMAGING CONDITION EFFECTS ON SHOT-PROFILE MIGRATION AMPLITUDES

EFECTOS DE LA CONDICIÓN DE IMAGEN TIPO DECONVOLUCIÓN EN LAS AMPLITUDES DE LA IMAGEN MIGRADA EN EL DOMINIO DE DISPARO COMÚN

Flor A. Vivas-Mejía^1*, Herling González-Alvarez¹, Ligia E. Jaimes-Osorio² and Nancy Espindola-López¹

¹Ecopetrol S.A. - Instituto Colombiano del Petróleo (ICP), A.A. 4185 Bucaramanga, Santander, Colombia
²Unión Temporal UP Consultorías, Bucaramanga, Santander, Colombia

E-mail: flor.vivas@ecopetrol.com.co

(Received Dec. 01, 2011; Accepted Nov. 02, 2012)

*To whom correspondence should be addressed

ABSTRACT

Amplitude preservation in Pre-Stack Depth Migration (PSDM) processes that use wave field extrapolation must be ensured – first, in the operators used to continue the wavefield in time or depth, and second, in the imaging condition used to estimate the reflectivity function. In the later point, the conventional correlation-type imaging condition must be replaced by a deconvolution-type imaging condition. Migration performed in common-shot profile domain obtains the final migrated image as the superposition of images resulting of migrate each shot separately. The amplitude obtained in a point of the migrated image corresponds to the sum of the reflectivities for each shot which has illuminated such point, along the angles determined by the velocity model and the positions of the source and the receiver. The deeper the reflector, the lower the amplitude of the illumination field will be. As result, the correlation-type imaging condition produces images with an unbalanced amplitude decrease with depth. A deconvolution-type imaging condition scales the amplitudes through a correlation, using the weighting function dependent on the spectral density or the illumination of the downgoing wave field. In this article, two possible scaling functions have been used in the case of a single shot. In the case of data with multiple shots, five scaling possibilities are presented with the spectral density or the illumination function. The results of applying these imaging conditions to synthetic data with multiple shots show that the values of the amplitude in the migrated images are influenced by the coverage of the common midpoint, compensating this effect only in one of the imaging conditions described. Numerical experiments with synthetic data generated using Seismic Unix and the Sigsbee2a data are presented, highlighting that in velocity fields with strong vertical and lateral velocity variations, the balance of the amplitudes of the deep reflectors relative to the shallow reflectors is strongly influenced by the imaging condition applied.

Keywords: Imaging condition, Preserving amplitudes, Seismic migration, Seismic processing.

RESUMEN

La preservación de amplitudes en los procesos PreStack Depth Migration (de las siglas en inglés PSDM) que utilizan extrapolación de campos de onda, se debe garantizar tanto en los operadores que son utilizados para continuar los campos en tiempo o profundidad, como en la condición de imagen que es utilizada para estimar la función de reflectividad, para lo cual la convencional condición de imagen de correlación debe ser remplazada por una condición de imagen tipo deconvolución. La migración realizada en el dominio de disparo común, obtiene la imagen migrada final como la superposición de las imágenes obtenidas de migrar los disparos separadamente. La amplitud obtenida en un punto de la imagen migrada corresponde a la suma de las reflectividades obtenidas para cada disparo que alcanza a iluminar dicho punto, a un ángulo determinado por el modelo de velocidades y las posiciones de la fuente y el receptor. Cuanto más profundos los reflectores, menores serán las amplitudes del campo de iluminación y por lo tanto una condición de imagen tipo correlación siempre producirá imágenes con amplitudes desbalanceadas que disminuyen con la profundidad. La condición de imagen tipo deconvolución busca realizar un escalamiento de las amplitudes obtenidas a través de la correlación, utilizando una función peso dependiente de la densidad espectral o la iluminación del campo descendente. En el caso de un único disparo, dos posibilidades de escalamiento han sido utilizadas. En el caso de datos con múltiples disparos se presentan cinco posibilidades de escalamiento con la densidad espectral o la función iluminación. Los resultados de la aplicación de estas condiciones de imagen a datos sintéticos con múltiples disparos muestran que los valores de amplitud en las imágenes migradas están influenciados por la cobertura del punto medio común, siendo compensado este efecto solamente en una de las condiciones de imagen descritas. Experimentos numéricos con datos sintéticos generados en Seismic Unix y con el dato Sigsbee2a son presentados, resaltando que en modelos con campos de velocidades que incluyen fuertes variaciones verticales y laterales de velocidad, el balance de las amplitudes de los reflectores profundos en relación a los reflectores rasos es fuertemente dependiente de la condición de imagen aplicada.

Palabras clave: Condición de imagen, Preservación de amplitudes, Migración sísmica, Procesamiento sísmico.

RESUMO

A preservação de amplitudes nos processos PreStack Depth Migration (PSDM pelas suas siglas em inglês) que utilizam extrapolação de campos de onda, deve-se garantir tantonos operadores que são utilizados para continuar os campos em tempo ou profundidade, como na condição de imagem que é utilizada para estimar a função de refletividade, para o qual a convencional condição de imagem de correlação deve ser substituída por uma condição de imagem tipo deconvolução. A migração realizada no domínio de disparo comum obtém a imagem migrada final, como a superposição das imagens obtidas de migrar os disparos separadamente. A amplidão obtida em um ponto da imagem migrada corresponde à soma das refletividades obtidas para cada disparo, que alcança a iluminar dito ponto a um ângulo determinado pelo modelo de velocidades e as posições da fonte e o receptor. Quanto mais profundos os refletores, menores serão as amplitudes do campo de iluminação e, portanto, uma condição de imagem tipo correlação sempre produzirá imagens com amplitudes desbalanceadas que diminuem com a profundidade. A condição de imagem tipo deconvolução busca realizar um escalamento das amplitudes obtidas através da correlação, utilizando una função de peso dependente da densidade espectral ou a iluminação do campo descendente. No caso de um único disparo, duas possibilidades de escalamento foram utilizadas. No caso de dados com múltiplos disparos se apresentam cinco possibilidades de escalamento com a densidade espectral ou a função iluminação. Os resultados da aplicação destas condições de imagem a dados sintéticos com múltiplos disparos mostram que os valores de amplidão nas imagens migradas estão influenciados pela cobertura do ponto médio comum, sendo compensado este efeito somente em uma das condições de imagem descritas. Experimentos numéricos com dados sintéticos gerados em Seismic Unix e com o dado Sigsbee2a são apresentados, ressaltando que em modelos com campos de velocidades que incluem fortes variações verticais e laterais de velocidade, o balanço das amplitudes dos refletores profundos em relação aos refletores rasos é fortemente dependente da condição de imagem aplicada.

Palavras chave: Condição de imagem, Preservação de amplitudes, Migração sísmica, Processamento sísmico.

INTRODUCTION

Amplitude-preserved PSDM processes has been developed to ensure the reliability of the results of the pre- and post-stack inversions such as Amplitude Variation with offset (AVO) analysis, acoustic and elastic inversion, etc. For instance, for meaningful acoustic inversion results, it is necessary that the seismic image of the subsurface be kinematically correct (from a structural viewpoint) and dynamically correct; in other words, amplitude values on the reflectors must estimate at best the reflectivity function and its geometry.

Pre-stack migration methods based on wave field extrapolation work in two stages. In the first stage, the fields of the source and of the receivers are respectively propagated and back-propagated. In the second stage, an imaging condition is applied, so that high seismic event correlation is present wherever there is an impedance contrast (Claerbout, 1985). Pre-stack migration based on the wave field extrapolation in depth (OWWE, One Way Wave Equation) is widely used for its advantage in computational time relative to the migration by extrapolation in time (RTM, Reverse Time Migration). This paper aims to study the imaging conditions applied in time frequency domain for OWWE migration methods. However, an extension of the presented imaging conditions can be done to RTM migration.

The OWWE do not propagate the wave field amplitudes properly (Wapenaar, 1990; Godin, 1999) and must therefore, be modified by introducing in the equations a new operator which includes lateral and vertical gradients of the velocity field. The new resulting equations are known as One-Way Wave Equation with True Amplitude (OWWE -TA) (Zhang, 1993; Zhang, Zhang & Bleistein, 2003; Vivas & Pestana, 2010).

A deconvolution-type imaging condition is needed to ensure obtaining the correct value of the reflectivity in the migrated image (Claerbout, 1985; Valenciano & Biondi, 2003; Guitton, Valenciano, Bevc & Claerbout, 2007; Chattopadhyay & McMechan, 2008). The deconvolution-type imaging condition scale the amplitudes through a correlation, using a weight function dependent on the illumination field. In data with a single shot and receivers covering the whole velocity field, there are two illumination-field weighting possibilities (Schleicher, Costa & Novais, 2008) and its equivalence has been proved (Cazzola, Arienti, Bonomi & Cardone, 2002; Shin, Jang & Min, 2001; Valenciano & Biondi, 2003; Vivas, Pestana & Bjorn, 2009).

In shot-profile migration each shot is migrated separately and the images of all shots are stacked to produce the final migrated image. The amplitude obtained at a point in the migrated image corresponds to the sum of the reflectivities obtained for each shot at an angle determined by the velocity model and the source and receiver positions. A second summation appears in the imaging condition, associated with the sum of the shots, that allows five possibilities of applying a deconvolution-type imaging condition and creates the possibility of other forms of stabilization.

We perform numerical experiments on synthetic data generated in Seismic Unix (Cohen & Stockwell, 2006) using three velocity fields: one displaying only vertical, a second one displaying vertical and lateral lineal gradients, and a third one using the Sigsbee2a model (Paffenholz, Stefani, McLain & Bishop, 2002). Results show that only three of these five conditions properly compensate for geometrical spreading. For the other two cases, significantly underestimated values for the reflection coefficient were obtained in the deeper reflectors. Additionally, the influence of the common image point redundancy on the reflection coefficient value is analyzed. It is shown that only two of the five image conditions proposed is this effect properly corrected, resulting in images with better reflector continuity.

2. BASICS OF TRUE AMPLITUDE OWWE MIGRATION

One-way Equations with True Amplitude

Migration by extrapolation of the wave fields in the depth direction is performed in two stages. In the first stage, the equations which model the propagation of the downgoing and upgoing wave field are solved:

where D_s and U_s are the downgoing and upgoing wave fields, x, z are the coordinates on surface and at depth respectively, the pseudo-differential operators Λ and Γ are given by:

Once the wave fields are extrapolated from the level z_j to z_j+1, the migration process is completed by applying a deconvolution imaging condition. For a single shot data:

For data with multiple shots, appears a double summation:

Operator Phase Shift (PS) with True Amplitude (PS+TA)

For a media that depends only on depth v = v(z), we can apply the Fourier transform in x and write the operators and the in the wave number (kx, z;w) domain in the form

The Equations 1 and 2 writtten in the domain (k_x, z;w) are expressed as,

The term γ in the Equations 7 and 8, can be eliminated through the introduction of the new variables

making unnecessary the direct numerical calculation of the derivative of the vertical velocity field and reducing the field extrapolation from the level z_j to the level z_j+1 to the product of the two factors, one associated with the phase correction and the other associated with the amplitude correction, in the form:

Phase Shift Plus Interpolation with True Amplitud (PSPI+TA)

In media with lateral variation of the velocity, v=v(x,z), a Phase Shift Plus Interpolation (PSPI) migration scheme (Gazdag & Sguazzero, 1984) is used. This scheme performs extrapolation in depth of the 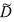and 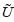wave fields from the level z_j to the level z_j+1 through a phase shift e^±iλ(zj)Δz in the (k_x; ω) domain. The operator λ(z_j) is calculated with n reference velocities, selected at each level z_j. The lateral variations of the velocity are introduced in the domain (x, ω) by interpolating the n wave fields, in accordance to the local velocity v(x).

To implement the PSPI migration based on the phase shift technique with true amplitude through Equation 10, it is necessary to apply the amplitude correction, so that m reference velocities at the z_j+1 level must be taken into account to evaluate λ_z+1 , thereby generating a set of N=m^*n fields to be interpolated.

A second alternative is to solve Equations 1 and 2 in two steps. Initially the PSPI scheme is used to obtain the wave fields 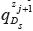and 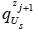, with a phase correction equivalent to the conventional algorithm. In a second step, the amplitude correction is applied on the fields 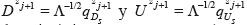in the (x, z, ω) domain (Vivas & Pestana, 2010).

3. DECONVOLUTION-TYPE IMAGING CONDITION

The correlation-type imaging conditions yield not accurate amplitudes and invalidate any further reflectivity inversion analysis. The deconvolution-type imaging conditions compensate the image correlation amplitudes through an illumination weighting function.

The deconvolution-type imaging condition for a single shot can be written in the following way:

where the term E within the sum corresponds to the spectral density of the downgoing wave field

The spectral density map E(x, z;ω) of going wave field, can reach very low or zero energy values in certain points, producing computational stability problems when performing division. Different techniques to solve this numerical instability, associated with rounding errors, have been proposed (Claerbout, 1971; Valenciano & Biondi, 2003; Vivas et al., 2009). In this work we use the stabilization technique of the imaging condition proposed by Vivas et al. (2009).

The stabilization of the image in Equation 11 is performed in the domain (x, z;ω), defining for each frequency an average value of the spectral density of the downgoing wave field

A cut-off criterion can be used to determine which points have good or bad spectral density E(x, z;ω)v=alDuess

Here, the imaging condition can be applied directly on the points with good spectral density, while on the points with bad spectral density the value is replaced by the average value. The value α is data dependent. Thus, a new map of spectral density E^-(x,z;ω)

A second stabilization option for the application of the imaging condition, consists in normalizing the correlation-type imaging condition by the illumination function of the shot I(x,z)=∑_ωE(X,Z;ω), obtaining:

The rationale for taking a separate sum over the frequency in the numerator and denominator in (Equation 16), is justified by the asymptotic approximation of the high frequencies in which E is independent of the frequency (Bleinstein, 2007) or from the point of view of the least squares inversion of the equation

where the reflectivity value given by Equation 16 minimizes the cost function

The imaging condition given by Equation 16 is more stable than that given by Equation 11 (Schleicher et al., 2008; Vivas et al., 2009), since in this case the stabilization involves the function I(x, z). Defining the median value of the illumination function at the level z as 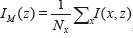, another cut-off criterion for determining the points with good or bad illumination could be established:

In the points with good illumination, the imaging codition might be applied directly, while in the points with bad illumination the value will be εI_M, forming a new illumination map:

The value of the constants α and ε must be less than one and are determined for each velocity field.

For data with multiple shots, the deconvolution-type imaging condition appears in the form

The presence of an additional sum over the shots in Equation 21, allows the formulation of the following two alternative imaging conditions:

The imaging condition in Equation 22 is equivalent to Equation 21 by the same arguments described in the imaging condition for a single shot. The imaging condition given by Equation 23 corresponds to a normalization of the correlation-type imaging condition through the total illumination function ∑_s ∑_ω^E(x,z;ω), so it is anticipated that it will suffer of the same drawbacks that the correlation-type imaging conditions, i.e. the amplitudes in the migrated image will not correspond to the expected values of the reflectivity function. However, the balance of the amplitudes recovered in the final image will be evaluated in the next section.

If the stabilization of the imaging condition is performed with the illumination function stabilization, two additional deconvolution-type imaging conditions will be obtained for data with multiple shots:

where the imaging condition in Equation 25 represents a normalization of the correlation-type imaging condition trough the modified total illumination function I = ∑_sI (x, z) and also is expected that does not properly correct the reflectivity function value.

From the imaging conditions given by Equations 22, 23, 24, and 25, is observed that the redundancy of the common image point influences the obtained reflectivity values. From Equation 22 and 24, is concluded that the points with less redundancy, i.e. lower total illumination, will have overestimated reflectivity values.

4. NUMERICAL EXPERIMENTS

With the goal of comparing the amplitudes obtained on reflectors in migrated images, it was used a synthetic data set composed of 250 shots and 49 geophones per shot in offsets ranging 40 m to 1.960 m. Data was generated using Seismic Unix (Cohen & Stockwell, 2006) through Kirchhoff modeling, where reflectors are introduced as a set of diffracting points within a media with velocity gradients.

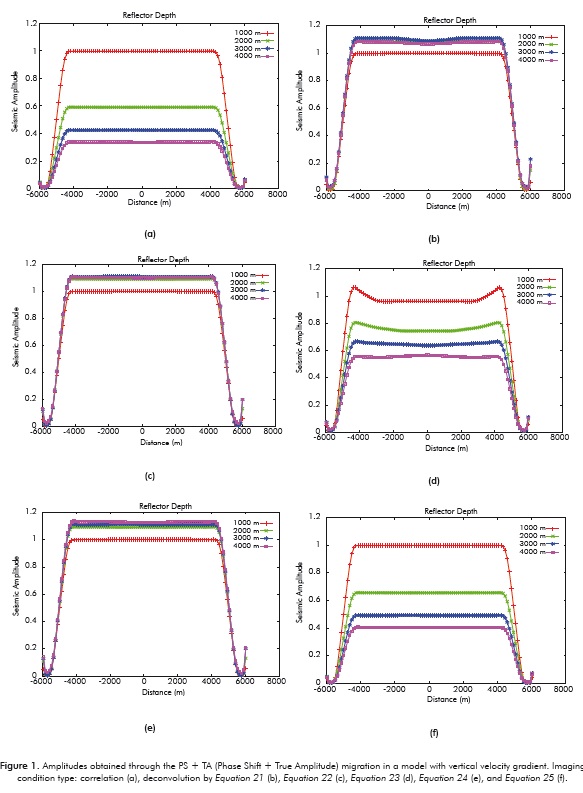
The first experiment was conducted in a velocity media that varies vertically as v(z) = 2000 + 0.3z. Four reflectors at depths 1000, 2000, 3000 and 4000 m and a predetermined reflectivity value equal to the unit were used. The PS + TA migration scheme described in section 2 (Pag. 7) was used. Figure 1 represents the amplitudes obtained on the reflectors applying the correlation-type imaging conditions (Figure 1a), and deconvolution-type imaging conditions (according to Equations 21-25, Figures 1b - f). It is observed that the amplitudes recovered through imaging conditions given by Equations 21, 22 and 24 are equivalent. Similarly, the equivalence of the correlation-type imaging condition with the total illumination normalization (Equation 25) is observed, where underestimation of reflectivity amplitudes is greater with depth.

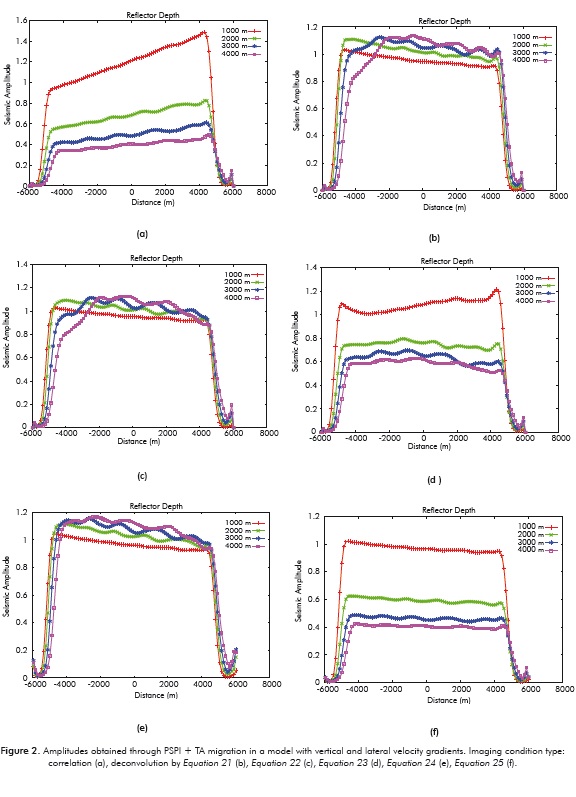
The second numerical experiment was conducted with the same acquisition geometry of the first experiment, in a velocity field with vertical and lateral gradient in the form v(x, z) = 2000 + 0.3z + 0.2x. The algorithm used for the migration was PSPI + TA.

It is observed in Figures 2d and 2f, that the deconvolution- type imaging conditions that compensate the amplitudes with a weight function for all the shots Equations 23 and 25) generate differences in amplitudes on the reflectors similar to those produced by the correlation-type imaging condition (Figure 2a). Figures 2b, 2c and 2e show once again that the imaging conditions given by Equations 21, 22 and 24, properly compensate the geometric spreading, as their amplitude values are close to unity on the reflectors. In the migrated image corresponding to the imaging condition given by Equation 24, Figure 2e, we can observe the correct compensation for the effect of the coverage on the reflection coefficient. This fact can improve the lateral continuity of the reflectors obtained on a migrated image from data with irregular coverage.

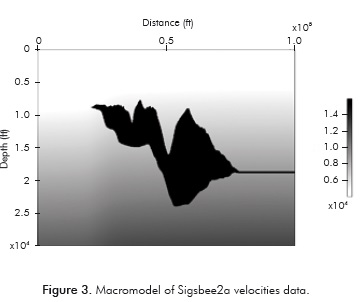
The third experiment corresponds to Sigsbee2a data migration (Paffenholz et al., 2002), generated synthetically from a geological model taken from the Sigsbee Escarpment Province in the Gulf of Mexico. Due to the complex shape of the salt body, there are problems of imaging formation and energy focalization in the deeper regions. This makes the data of great interest for testing of migration algorithms with offshore data.

The velocity model used for the migration is presented in Figure 3.

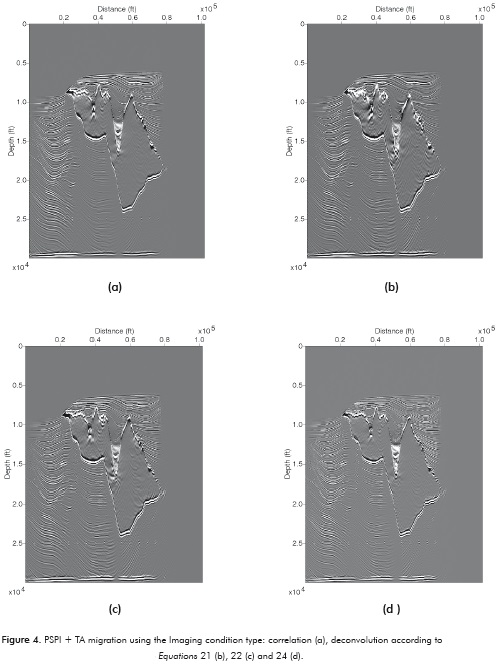
Figure 4a shows the image obtained by migration using correlation-type imaging conditions. Figures 4b, 4c, and 4d represent the images obtained through the application of the three deconvolution-type imaging conditions given by Equations 21, 22 and 24 respectively.

The four images obtained by migration (Figure 4) are significantly different in the amplitudes of the reflectors beneath the salt body. Notice the unbalance between shallow and deep reflectors in the image obtained by the correlation-type imaging condition (Figure 4a). The images obtained by a deconvolution-type imaging condition present better continuity and balance of the amplitudes in deep reflectors. However, in the image obtained through the application of a shot by shot deconvolution-type imaging condition (Equation 21, Figure 4b) lower image vertical resolution is observed, because the stabilization process modifies the spectral density of the downgoing field with a constant value that does not discriminate frequencies yielding a filter effect.

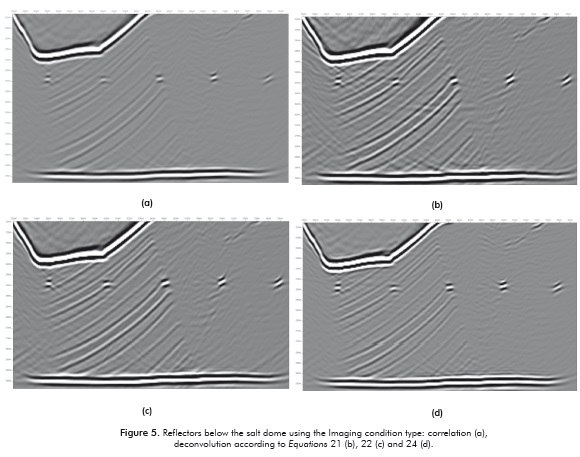
A zoom view of the reflectors in the deepest part of the model, beneath the salt body, is presented (Figure 5). Notice that the two deconvolution-type imaging conditions that best recover the amplitudes correspond to Equations 22 and 24, Figures 5c and 5d. This result confirms that for data with irregular coverage, the imaging condition of Equation 24 will produce the best results.

5. CONCLUSIONS

• Of the five deconvolution-type imaging conditions presented for application to the migration of data with multiple shots, it is shown that only three obtain reflectivity values near to the expected values, properly compensating for geometric spreading. The other two imaging conditions correspond to a scaling of the correlation-type imaging condition.
• For multiple shots, the amplitude values obtained for the reflection coefficients at a given point of the image are influenced by the redundancy of the common image point, and only one of the three imaging conditions that preserve the amplitude compensates this effect correctly. In real data with irregular redundancy of the common image point, this imaging condition should improve the lateral continuity of the reflectors.
• Applying a deconvolution-type imaging condition in real data will help to a better balance of the amplitudes, highlighting the deep reflectors located beneath complex velocity fields (i.e. salt bodies). In addition to this gain from a kinematic point of view, more reliable amplitude values for post-stack inversion processes must be obtained.

ACKNOWLEDGEMENTS

The authors thank Ecopetrol S.A. for its support in the development of this work, both its employees as well as the graduate student for fellowship and an anonymous referee for their constructive reviews.

REFERENCES

Bleistein, N. (2007). On stabilizing Kirchhoff-type inversion formulas. Making waves about seismics workshop, WIT Consortium (abstract).         [ Links ]

Cazzola, L., Arienti, M.T., Bonomi, E. & Cardone, G. (2002). Amplitude preserving Monte Carlo 3D pre-stack migration. 64th EAGE Conference & Exhibition, Pre-stack Time Imaging.         [ Links ]

Cohen, J. & Stockwell, Jr. (2006). Seismic Un^*x: a free package for seismic research and processing. Toulsa: Center for Wave Phenomena, Colorado School of Mines. Release No. 39- 2006.         [ Links ]

Chattopadhyay, S. & McMechan, A. (2008). Imaging conditions for prestack reserve time migration. Geophysics, 73(3), 581- 589.         [ Links ]

Claerbout, J. (1971). Toward a unified theory of reflector mapping. Geophysics, 36(3), 467-481.         [ Links ]

Claerbout, J. (1985). Imaging the earth's interior. New York: Blackwell Scientific Publications.         [ Links ]

Gazdag, J. & Sguazzero, P. (1984). Migration of seismic data by phase shift plus interpolation. Geophysics, 49(2), 124-131.         [ Links ]

Godin, O.A. (1999). Reciprocity and energy conservation within the parabolic approximation. Wave Motion, 29(2), 175-194.         [ Links ]

Guitton, A., Valenciano, A., Bevc, D. & Claerbout, J. (2007) Smoothing imaging condition for shot-profile migration. Geophysics, 72(3), S149-S154.         [ Links ]

Paffenholz, J., Stefani, J., McLain, B. & Bishop, K. (2002). SIGSBEE2a Synthetic subsalt dataset: image quality as function of migration algorithm and velocity model error. 64th EAGE Conference, Extended abstracts.         [ Links ]

Schleicher, J., Costa, J. & Novais, A. (2008). A comparison of imaging conditions for wave-equation shot-profile migration. Geophysics, 73(6), S219- S227.         [ Links ]

Shin, C., Jang, S. & Min, D. J. (2001). Improved amplitude preservation for pre-stack depth migration by inverse scattering theory. Geophysical Prospecting, 49(5), 592-606.         [ Links ]

Valenciano, A. & Biondi, B. (2003). 2D Deconvolution imaging condition for shot-profile migration. SEG Technical Program, 22(1).         [ Links ]

Vivas, F. & Pestana, R. (2010). True amplitude one-way wave equation migration in the mixed domain. Geophysics, 75(5), S199-S209.         [ Links ]

Vivas, F., Pestana, R. C. & Bjorn, U. (2009). A new stabilized least-squares imaging condition. J. of Geophysics and Eng., 6(3), 264-268.         [ Links ]

Wapenaar, C. (1990). Representation of seismic sources in the one-way wave equations. Geophysics, 55(6), 786-790.         [ Links ]

Zhang, G. (1993). System of coupled equations for up-going and down-going waves. Acta Math. Appl. Sinica, 16(2), 251-263.         [ Links ]

Zhang, Y., Zhang, G. & Bleistein, N. (2003). True amplitude wave equation migration arising from true amplitude oneway wave equations. Inverse Problems, 19(5), 1113-1138.         [ Links ]