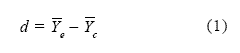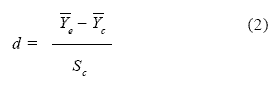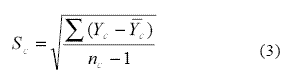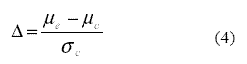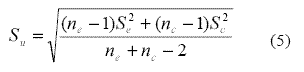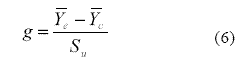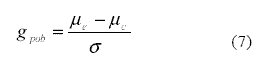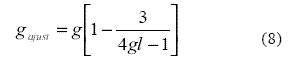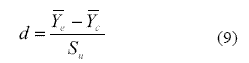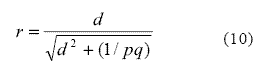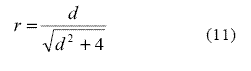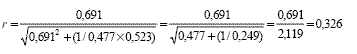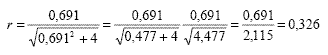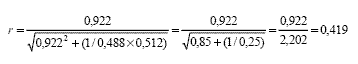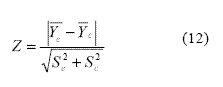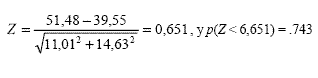Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista Latinoamericana de Psicología
Print version ISSN 0120-0534
rev.latinoam.psicol. vol.40 no.3 Bogotá Sept./Dec. 2008
TAMAÑO DEL EFECTO: REVISIÓN TEÓRICA Y APLICACIONES
CON EL SISTEMA ESTADÍSTICO ViSta
EFFECT SIZE: A CONCEPTUAL REVIEW AND APPLICATIONS WITH THE VISTA STATISTICAL SYSTEM
RUBÉN LEDESMA
CONICET/Universidad Nacional de Mar del Plata, Argentina
GUILLERMO MACBETH
CONICET/Instituto de Investigaciones Psicológicas de la Universidad del Salvador, Argentina y
NURIA CORTADA DE KOHAN1
Universidad de Buenos Aires, Argentina
1 Correspondencia: NURIA CORTADA DE KOHAN, Salguero 1692, 8-A, CP 1425, Buenos Aires, Argentina. Tel. 54-011 4824- 1753. Correo electrónico: ncortada@psi.uba.ar
ABSTRACT
Effect size (ES) is a necessary complement to the statistical hypothesis testing, however, researchers rarely report ES in their papers. This work provides a conceptual review of the ES estimates for the difference between two means, taking into account the most important algorithms and their interpretation. We also provide a guide to the freely available and easy-touse ViSta statistical software to compute ES. We hope this paper contributes to the diffusion of ES methods and encourages its use among researchers in Psychology.
Key words: effect size, mean, free software, ViSta.
RESUMEN
La estimación del tamaño del efecto (TE) se considera actualmente como un complemento necesario a las pruebas de hipótesis, no obstante, su uso se encuentra aún poco extendido entre los investigadores en Psicología. Este trabajo ofrece una revisión teórica de las estimaciones del TE para el caso de la diferencia entre dos medias, considerando los algoritmos más importantes y su interpretación. Complementariamente, se presenta y describe un nuevo programa para el cálculo del TE dentro del sistema ViSta. Este programa es simple de utilizar y se encuentra
disponible de forma gratuita. Se espera que el trabajo contribuya a difundir estos procedimientos y aliente su uso entre los investigadores en Psicología.
Palabras clave: tamaño del efecto, medias, software libre, ViSta.
INTRODUCCIÓN
El tamaño del efecto (TE): definición e importancia
La investigación psicológica se interesa por detectar la ocurrencia de ciertos fenómenos poblacionales mediante el análisis de una colección de datos muestrales (Cohen, 1988; citado por Kohan, 1994). Para lograr tal conocimiento se vale de un procedimiento lógico-estadístico que permite decidir, con cierto margen de error, si es posible sostener o no la ocurrencia poblacional del fenómeno bajo estudio. Lo que interesa saber es, por ejemplo, si un tratamiento novedoso A es mejor que un tratamiento clásico B para la recuperación de personas que padecen algún trastorno. Resulta pertinente estudiar si los pacientes tratados con A mejoran más que los tratados con B y la medida en que tal diferencia se presenta en la población, más allá de lo que se observa en la muestra que el investigador conoce.
El tamaño del efecto (TE) se define como el grado de generalidad que posee esa superioridad de A sobre B en la población de la que se obtuvo la muestra estudiada. De esta manera, el TE se refiere a la magnitud de un efecto que es, en este ejemplo, la diferencia entre un tratamiento nuevo A y otro clásico B. Si A es realmente mejor que B, interesa saber en qué medida se espera este fenómeno en la población (Cohen, 1992b). No es suficiente saber que la mejoría media lograda con A es mayor que la mejoría media lograda con B en un experimento particular. Se necesita saber, además, hasta dónde se puede generalizar este hallazgo cuando se tie nen en cuenta las limitaciones del experimento. La cantidad reducida de personas que participaron del estudio, el máximo riesgo que se acepta correr en la generalización y los errores de medición de la mejoría, entre otras, son las limitaciones del experimento que restringen la posibilidad de afirmar la superioridad de A sobre B para la población de la que se obtuvieron las personas que participaron del estudio.
En síntesis, no es suficiente con identificar la ocurrencia de cierto efecto, se requiere adicionalmente determinar su magnitud o tamaño (Cohen, 1990, 1992a). Con tal propósito se han desarrollado diversas técnicas formales que permiten cuantificar el TE para diversas pruebas estadísticas habituales en la investigación psicológica como son, por ejemplo, la prueba t, el análisis correlacional r, y el análisis de varianza, entre otras (Cohen, 1988). Estas técnicas de estimación del TE poseen interés práctico en Psicología, no sólo como complemento necesario a la pruebas de hipótesis, sino también porque ofrecen una métrica n sobre la cual integrar los resultados de la investigación en estudios de meta-análisis (Anderson, 1999; Macbeth, citado por Kohan & Razumiejczyk, en prensa). Este interés ha llevado a la American Psychological Associcomúation (APA) a alentar su uso entre los investigadores en Psicología (Thompson, 1998) y también a que las publicaciones periódicas soliciten, cada vez más, no solo estadísticas, sino también sus TE (Hunter & Schmidt, 2004).
No obstante el interés asociado con estas técnicas, en la práctica su uso sigue siendo poco habitual entre los investigadores, quienes se muestran más proclives a informar sólo los valores de significación de las pruebas estadísticas, es decir, el valor convencional de a fijado en 0,01 ó 0,05 (Cohen, 1990, 1994; citado por Kohan, 2006). Una cuestión añadida y que no contribuye a modificar esta práctica, es que los programas más populares no siempre incluyen la estimación del TE entre sus opciones de análisis. Así, resulta clara la conveniencia de insistir en la difusión de estas metodologías, tanto como facilitar el acceso a las tecnologías informáticas necesarias para su aplicación.
En este contexto, se presenta en lo que sigue una revisión teórica de las estimaciones del TE para el caso de la diferencia entre dos medias. Esta revisión incluye una presentación de los algoritmos más comunes, su cálculo y su interpretación. Luego, se introduce y describe un procedimiento para estimar el TE mediante el programa ViSta The Visual Statistics System (Young, 1996). Se espera que el trabajo contribuya a una mayor difusión de estas metodologías y aliente su uso entre los investigadores en Psicología.
ESTIMACIONES DEL TE: EL CASO DE LA DIFERENCIA ENTRE DOS MEDIAS
Para calcular el TE que surge de la diferencia entre dos medias, se emplean habitualmente tres procedimientos que se conocen como delta de Glass, d de Cohen y g de Hedges (Grissom & Kim, 2005). A estos algoritmos se agregan la conversión de d en r, que es la medida más común en la investigación psicológica actual y el estadístico CL (Common Language Effect Size Statistic), menos conocido pero que también puede resultar de utilidad. Mediante estos estimadores se calcula el grado de generalidad poblacional de un efecto, a partir de la diferencia que se observa entre dos medias muestrales. La preferencia por una u otra depende de ciertas condiciones vinculadas a los supuestos de las distribuciones y a las propiedades del diseño de investigación.
La delta de Glass
Pretende estudiar el efecto de la manipulación de la variable independiente X sobre la variable dependiente Y. Para ello se conforman dos grupos homogéneos de participantes. El grupo experimental recibe la manipulación de X mientras que el grupo control no la recibe. Se comparan la media de Y en el grupo experimental (Yc) con la media de Y en el grupo control (Ye) para saber si se generó entre ambas una diferencia d (Ecuación 1 ).
La diferencia d entre las medias de ambos grupos que genera la Ecuación 1 no es una medida estable y homogénea porque depende, entre otras condiciones, de la unidad de medida de la escala que se aplique para medir la variable dependiente. No es lo mismo una escala que puntúa de 1 a 10, que otra escala que puntúa, por ejemplo, de 1 a 100. Esta diferencia bruta d resulta demasiado libre como para obtener de ella alguna información útil, por lo que conviene uniformarla de algún modo que facilite su manejo. Su comportamiento se vuelve más informativo si se trata esta medida como un puntaje Z, es decir, cuando se la estandariza. La Ecuación 2 presenta la diferencia d estandarizada, lo que equivale a dividirla por el desvío estándar del grupo control (Sc).
El desvío estándar S de la Ecuación 2 se ajusta mejor con n - 1 en el denominador, tal como se indica en la Ecuación 3. El término n se refiere al tamaño del grupo control.
La diferencia estandarizada entre medias muestrales de la Ecuación 2 es un estimador del parámetro poblacional delta, atribuido a Gene Glass (Glass, McGaw & Smith, 1981), que se representa con la letra mayúscula griega ? en la Ecuación 4.Los valores de µe y µc se refieren a las respectivas medias poblacionales de la variable dependiente Y en los grupos experimental y control. La sigma con subíndice c (s c) se refiere al desvío estándar poblacional del grupo control. La ? poblacional de la Ecuación 4 es el parámetro que se pretende conocer mediante el cálculo del estadístico muestral de la Ecuación 2. La escala dentro de la que se mueve la ? es la de los puntajes Z, es decir, cada unidad es un desvío estándar. Su interpretación se refiere a la distancia estandarizada que la manipulación de la variable independiente X generó en la variable dependiente Y. Por ejemplo, si ? = 1, se interpreta que la media del grupo experimental (esto es, en condición de manipulación de X) se encuentra a 1 desvío estándar de la media del grupo control, es decir, la primera supera aproximadamente al 84% del grupo control (porque el área bajo la curva normal que corresponde a una Z = 1 de la distribución estandarizada de µc es de p = 0,84022).
La g de Hedges
La delta de Glass pondera la diferencia entre los grupos mediante el desvío estándar del grupo control Sc, como se indica en el denominador de la Ecuación 2. Sin embargo, la diferencia bruta entre las medias del numerador depende de la variabilidad de los dos grupos. De esta manera, la delta de Glass es poco sensible a las diferencias de variabilidad (por ejemplo, desvío estándar, varianza) entre los grupos experimental y control. Este conservadurismo puede generar sesgos en la estimación del TE cuando la variabilidad resulta heterogénea entre los grupos. Es por ello que Hedges propuso cambiar el desvío estándar del grupo experimental Sc que se presenta en el denominador de la Ecuación 2, por otro desvío estándar que mida la variabilidad conjunta de ambos grupos (Grissom & Kim, 2005). Esta medida de variabilidad unificada S es un nuevo desvío estándar que se obtiene de combinar los datos de los grupos experimental y control en una única medida que no asume la igualdad de varianzas. El desvío estándar unificado Su se obtiene mediante los cómputos de la Ecuación 5.
El desvío estándar unificado Su permite que tanto la variabilidad interna de cada grupo (S2e, S2c), como el tamaño de los grupos (ne, nc) participen en la estimación del TE. Esta medida resulta menos sesgada que la delta de Glass cuando no se asume la igualdad de varianzas. El empleo del desvío estándar unificado Su para el cálculo del TE, cuando se comparan dos grupos independientes, se conoce como la g de Hedges. Su cómputo se presenta en la Ecuación 6.
La g de Hedges es un estimador de la correspondiente g poblacional gpob que se indica en la Ecuación 7.
Tanto la delta de Glass, como la g de Hedges, presentan un sesgo positivo, es decir, una sobreestimación del TE que puede corregirse mediante un ajuste propuesto por el mismo Hedges. La g ajustada g ajust se obtiene mediante la Ecuación 8.
A mayor cantidad de grados de libertad gl, menor ajuste se necesita para lograr una estimación menos sesgada del TE, tal como se deduce de la ubicación de los gl en los cómputos de la Ecuación 8.
La d de Cohen
El estimador del TE propuesto por Cohen (1988, 1992a, 1994) es similar a la g de Hedges, aunque presenta un mayor sesgo cuando no se asume la igualdad de varianzas. El denominador de la g de Hedges que se presenta en la Ecuación 5, emplea el artificio de n - 1 (es decir, ne + nc 2) para lograr una mejor aproximación del valor muestral del desvío estándar unificado S u al valor poblacional del desvío estándar unificado s. Se ha demostrado que mediante este artificio se logra una mejor aproximación estadística a los valores poblacionales, que mediante el uso de n. Sin embargo, si las condiciones de variabilidad controlada que se proponen lograr los diseños experimentales son adecuadas, ambos artificios resultan equivalentes. Es por ello que bajo el supuesto del control ideal de todas las fuentes de variabilidad ajenas a la manipulación de la variable independiente X, se considera que el empleo de la n en el denominador del desvío estándar resulta pertinente. La d de Cohen, entonces, emplea este artificio para el cálculo del TE. El desvío estándar de la d de Cohen es, como ocurre con la g de Hedges que se presenta en las Ecuaciones 5 y 6, una medida que combina los desvíos estándar de los dos grupos, aunque la d no emplea el artificio de n - 1.
La d de Cohen (1988) es una de las medidas más empleadas en las publicaciones especializadas para el cálculo del TE y en los estudios meta-analíticos (Anderson, 1999; Hunter & Schmidt, 2004). Su cómputo se presenta en la Ecuación 9.
El desvío estándar unificado S u en la d de Cohen, sin embargo, no es idéntico al de la g de Hedges de la Ecuación 5, porque el primero emplea sólo la n, es decir, no incluye la corrección de n - 1.
La relación entre estas tres medidas del TE depende de la variabilidad interna de cada grupo. Cuanto más se aproximen los grupos experi mental y control a la normalidad y homogeneidad, más se acercarán al ideal de ? = gpob = g = d. Esta situación ideal resulta, sin embargo, poco posible debido a las variaciones que genera el error de muestreo, entendido como el conjunto de diferencias que se observan entre diversas muestras aleatorias obtenidas de una misma población (Hunter & Schmidt, 2004). Es poco probable que Se = Sc y, por lo tanto, que ambas medidas sean iguales a la sigma unificada poblacional s u.
Interpretación de las estimaciones del tamaño del efecto
El significado del TE no se obtiene mecánicamente (Cohen, 1990). Si bien su unidad de medida es la de los desvíos estándar, su interpretación depende de la manera en que se relaciona con otros criterios relevantes del razonamiento estadístico (Gigerenzer, 1993; Krueger, 2001; Thompson, 1998). Un mismo TE puede tener diferentes significados prácticos porque depende del problema específico que se esté evaluando. Uno de los aspectos más relevantes para la interpretación del TE es su relación con el poder estadístico (Cohen, 1988), entendido como la probabilidad que posee una prueba de obtener resultados significativos. Formalmente, el poder o potencia (power) se define como 1 - ß, siendo ß la probabilidad de aceptar erróneamente la hipótesis nula (Cohen, 1992a). A su vez, el poder estadístico es una función matemática que depende del tamaño de la muestra (n), del nivel de significación estadística a (p valor) y del TE. De esta manera, el TE ha sido entendido como un complemento necesario para el análisis de los datos empíricos en la prueba de hipótesis tradicional (Cortina & Dunlap, 1997).
En relación con este procedimiento clásico de la prueba de hipótesis, la hipótesis nula sostiene que el TE es igual a cero (Cohen, 1988, 1994). El alejamiento del TE de cero implica el rechazo de la hipótesis nula, por lo cual su magnitud crece junto con el poder de la prueba de significación estadística que se esté empleando. A mayor TE, mayor poder, es decir, menor probabilidad de cometer un error de tipo II. La consideración del TE en el contexto de la prueba de hipótesis es una manera de controlar tanto el valor de a (probabilidad de cometer un error de tipo I), como el valor de ß (probabilidad de cometer un error de tipo II). De esta manera, cuanto mayor sea el TE, menor resulta el tamaño de la muestra que se necesita para detectar la ocurrencia poblacional de un fenómeno.
El tamaño del efecto en términos de correlación
La forma más universal del TE es r, entendida como correlación biserial entre una variable independiente binaria X y una variable dependiente numérica o escalar Y (Cohen, 1988). La X adquiere sólo dos valores, por ejemplo 1 y 0, según la pertenencia del participante al grupo experimental (X = 1) o al grupo control (X = 0). Los valores de Y dependen, en cambio, de la escala de medición que se aplique. La estimación del TE mediante r tienen varias ventajas sobre los anteriores estimadores, entre las que se destaca su mayor facilidad de interpretación. Esta ventaja se debe a la condición acotada de la escala de r. La correlación es siempre un número decimal que fluctúa entre 0 y 1, a diferencia de las otras medidas del TE que se comportan como un puntaje Z. Por ello, es útil convertir estimadores como la d de Cohen a r. Esta conversión facilita, además, la posterior realización de estudios meta-analíticos. Cohen (1988) propone la fórmula de la Ecuación 10 para convertir la d en r.
Los valores de p y q corresponden a las proporciones de sujetos que pertenecen a los grupos experimental y control, respectivamente. Es decir que la proporción p es equivalente al cociente que surge de dividir la cantidad de sujetos que incluye el grupo experimental ne por la cantidad total de sujetos n (grupo experimental ne + grupo control nc). Es decir, p = ne / n. La proporción de sujetos que pertenecen al grupo control es q = nc / n. De esta manera, la proporción q es el complemento de p, por lo cual q = 1-p. Cuando el tamaño de ambos grupos es idéntico (ne = nc), el valor del término (1 / pq) resulta igual a 4, es decir 1 / (0,5 x 0,5) = 1/ 0,25 = 4. De esta manera, la Ecuación 10 puede abreviarse cuando los grupos experimental y control poseen el mismo tamaño. La Ecuación 11 propuesta por Cohen (1988) resume este caso.
Cuánto mayor sea la discrepancia entre p y q, es decir, entre el tamaño de los grupos experimental y control, mayor será el valor del denominador en la Ecuación 10, por lo cual menor será la correlación r.
Para interpretar el TE mediante r se debe considerar que a mayor TE, mayor r. Se infiere que cuanto mayor es el valor de r, mayor es la magnitud del efecto que la manipulación de la variable independiente X generó sobre la variable dependiente Y. A mayor valor de d (y mayor homogeneidad de tamaño entre los grupos), mayor correlación biserial entre X e Y. Supongamos el ejemplo que se reproduce con mayor detalle en el apartado de descripción del programa. En él, se realiza un experimento con dos grupos de similar tamaño, con 21 sujetos que recibieron una manipulación experimental y 23 sujetos que no recibieron ninguna manipulación y el TE obtenido para la diferencia estandarizada entre medias resulta de d = 0,691. Reemplazando los valores correspondientes en la Ecuación 10 obtenemos:
La Ecuación 11, que asume la homogeneidad del tamaño de los grupos, también arroja una r de 0,326 porque la diferencia de la n entre ambos es muy pequeña (p ˜ q ˜ 0,5).
Nótese que el término de mayor peso en estas fórmulas de conversión es el tamaño del efecto d. De esta manera, a mayor TE, mayor r, es decir mayor proximidad de r a 1. Si en el caso ilustrado elimináramos del grupo control un aparente outlier presente en los datos, la d ascendería de 0,691 a 0,922 y se obtendría una r aún mayor con la Ecuación 10:
La proporción p se obtiene de 21/43 = 0,488 y la proporción q se obtiene de 22/43 = 0,512, por lo cual el valor de pq resulta de 0,488 x 0,512 = 0,2498 ˜ 0,25. En este caso, la diferencia de tamaño entre los grupos experimental y control es tan pequeña que el valor de r resulta equivalente según las Ecuación 10 y Ecuación 11. El valor hallado de r = 0,419 indica una buena correlación entre la manipulación de X y las variaciones de Y. De esta manera, la conversión de d a r permite interpretar el TE en términos de correlación.
Tablas para la interpretación del tamaño del efecto
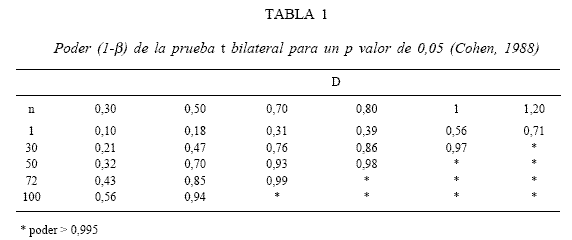
Cohen (1988) ha proporcionado una colección de tablas para la interpretación del TE en las pruebas estadísticas más usadas en la investigación psicológica, tales como t, r, ?2 , F, etc. Estas tablas presentan dos variedades: a) algunas sirven para calcular el poder de una prueba estadística en un análisis post hoc, es decir, luego de concluida la investigación; y b) otras se aplican para calcular el tamaño de muestra (n) necesario para detectar un TE determinado durante la planificación de un estudio, es decir, antes de la investigación (Citado por Kohan & Macbeth, 2008, en prensa). Las tablas que ofrece Cohen (1988) para el primer caso informan los valores aproximados del poder de la prueba para diferentes tamaños de la muestra n y diferentes valores del TE. En la Tabla 1 se resumen algunos valores del poder de la prueba t ofrecidos por Cohen para el caso de un criterio de significación de a = 0,05 en la comparación de dos grupos independientes. Los diversos TE (d) obtenidos se indican en las columnas y los diferentes tamaños de (n) se indican en las filas.
La Tabla 1 es una versión abreviada de la tabla ofrecida por Cohen (1988, pp. 36) para la estimación del poder de la prueba t bilateral con un p valor de 0,05 para la comparación de dos grupos independientes.
Para ilustrar el funcionamiento de esta tabla, Cohen propone un ejemplo en el que se comparan dos grupos de ratas en un experimento sobre aprendizaje. El grupo experimental fue sometido a una sesión de aprendizaje mientras que el grupo control no recibió ningún tratamiento. Se midió el número de ensayos necesarios para obtener éxito sostenido en una determinada tarea. Se encontró que las diferencias entre el grupo control y el grupo experimental arrojaron una estimación del TE equivalente a d = 0,50; con una n = 30 para cada grupo. El poder de la prueba estadística aplicada es, según la Tabla 1, equivalente a 0,47. Esto significa que la probabilidad de detectar un TE de 0,50 con un p valor de 0,05 mediante una prueba t bilateral es menor a 1/2. Si el tamaño del efecto resulta, en cambio, de mayor magnitud, entonces el poder aumenta.
Por ejemplo, si la d asciende de 0,50 a 0,70, manteniendo constante el resto de las condiciones, entonces el poder de la prueba corresponde a 0,76. Esto indicaría que la prueba t posee, en tal caso, una probabilidad bastante alta de detectar el TE especificado. El poder de la prueba aumenta junto con el tamaño de los grupos y, simultáneamente, a medida que aumenta la diferencia d entre el grupo experimental y el grupo control.
En general, a mayor TE y mayor tamaño de la muestra, mayor poder estadístico posee la prueba que se emplee para una hipótesis.
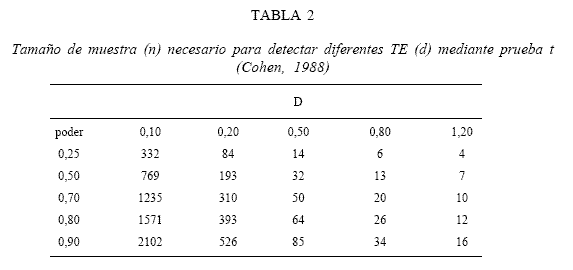
La segunda variedad de tablas ofrecidas por Cohen para interpretar el TE se relaciona con el cálculo del tamaño de la muestra que se necesita para detectar un determinado efecto. Estas tablas se emplean durante la planificación de un estudio. La Tabla 2 presenta una versión abreviada de la tabla ofrecida por Cohen (1988, pp. 55) para el cálculo del tamaño de la muestra que se necesita para detectar diferentes TE (d) según el poder estadístico de la prueba t bilateral con un p valor de 0,05. Por ejemplo, para detectar una diferencia estandarizada entre las medias del grupo experimental y control equivalente a una d = 0,50 con un poder de 0,80, se necesitan 64 casos por grupo. Si se espera que la diferencia entre los grupos resulte aún mayor, por ejemplo de d = 0,80, entonces se necesitarán menos casos, 26 por grupo según se indica en la Tabla 2. Con sólo 12 casos por grupo se podrá detectar una diferencia d = 1,20.
De la misma manera, en caso de anticipar una diferencia menor entre ambos grupos equivalente, por ejemplo, a una d = 0,20, se necesitarán 393 casos por grupo para que la prueba t bilateral (con un p valor 0,05) tenga un poder o probabilidad de 0,80 de detectarla. En general, a mayor poder, se necesita mayor cantidad de casos y, a mayor TE, menor cantidad.
El estadístico CL como una vía más simple de interpretación del TE
McGraw y Wong (1992) proponen otro método de estimación del TE para el caso de la diferencia entre dos medias provenientes de muestras independientes: el estadístico CL (Common Language Effect Size). Los autores argumentan que es un estadístico más simple de interpretar que los anteriores, ya que se expresa la magnitud de la diferencia en términos de un valor de probabilidad. En particular, estima la probabilidad de obtener un valor de diferencias entre medias mayor que cero en una distribución normal cuya media es la diferencia observada entre ambas medias (Valera-Espín & Sánchez-Meca, 1997). Para su cálculo, debe obtenerse primero:
Posteriormente se busca en la distribución normal tipificada la probabilidad de un valor menor al obtenido en la formula anterior. En el ejemplo supuesto y descrito en el próximo apartado del software, esto sería:
Que se interpretaría fácilmente como: el 74% de las veces un sujeto extraído al azar del grupo Experimental obtendrá un valor mayor que un sujeto extraído al azar del grupo Control. Esta conversión del TE a un valor de probabilidad podría aplicarse también a otras formas estandarizadas de estimación de TE, como el estadístico d de Cohen, para proporcionar una forma más universal de interpretación.
CÁLCULO DEL TE CON EL PROGRAMA ViSta
ViSta "The Visual Statistics System"
ViSta es un programa estadístico creado por el Profesor Forrest W. Young de la Universidad de Carolina del Norte en Chapel Hill (Young, 1996). Diseñado originalmente como entorno para desarrollar técnicas de visualización de datos, en la actualidad puede considerarse un sistema estadístico completo, ya que ofrece capacidades de edición, transformación y análisis de datos (Molina-Ibañez, Ledesma, Valero-Mora & Young, 2005). ViSta es un sistema escrito en lenguaje LispStat (Tierney, 1990) que ha sido pensado como software abierto y extensible, esto significa que proporciona acceso al código fuente y herramientas de programación para que los usuarios avanzados puedan expandir o modificar las capacidades de análisis del programa. Se presenta en este artículo la anexión de funciones básicas de estimación del TE a un módulo ya existente en ViSta para la comparación de medias.
Ejemplo de uso de ViSta
La Figura 1 muestra una imagen parcial de ViSta con un conjunto de datos apropiados para ilustrar el cálculo del TE. Este archivo de datos se encuentra en la librería de datos de ViSta y corresponde a un ejemplo tomado de Moore y McCabe (1993). Los datos pertenecen a un estudio que examina cómo una nueva tarea dirigida puede ayudar a los estudiantes a mejorar sus habilidades de lectura. Los dos grupos corresponden a estudiantes que han recibido la tarea (grupo experimental; ne = 21) y estudiantes que no la han recibido (grupo control; nc = 23). La variable dependiente en este caso es la puntación en un Test de Lectura, etiquetada en la imagen con el nombre Puntajes. Este tipo de archivo de datos puede crearse en ViSta usando el editor de datos o también importarse en formato texto.
En ViSta la estimación del TE se realiza automáticamente cuando se aplica el comando de contrastación de medias para muestras independientes. Por su naturaleza, este análisis solo admite datos de entrada con una variable independiente binaria -dos grupos de comparación- y una variable dependiente numérica, como los datos del ejemplo. Luego de ejecutar este comando, ViSta proporciona salidas numéricas en formato de texto (Reports) y salidas en formato gráfico para explorar visualmente los resultados del análisis.
La Tabla 3 muestra el informe con los resultados estadísticos básicos de la prueba de comparación de medias para los datos del ejemplo. La primera parte incluye información descriptiva (tamaño de los grupos, medias, desvíos estándar, etc.), mientras que la segunda parte muestra las diferentes formas de estimación del TE, incluyendo la d de Cohen (0,691), la g de Hedges (0,684), la delta de Glass (0,580), la conversión de d a r (0,326) y el estadístico CL (0,687). Por último, se presentan los resultados de la prueba t y de la prueba de homogeneidad de varianzas. Esta última parece indicar una diferencia significativa entre las varianzas de ambos grupos, y la consiguiente necesidad de una inspección más detallada y directa de los datos. Con este fin, puede ser conveniente utilizar los gráficos que ViSta proporciona para realizar un análisis exploratorio.
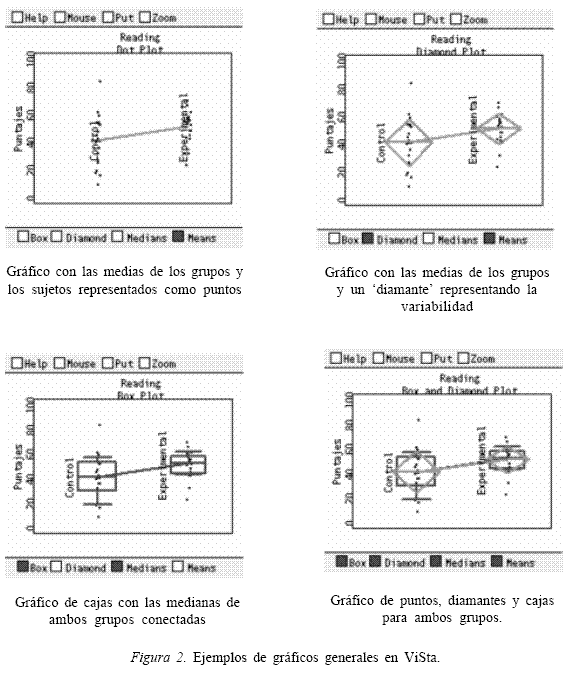
Para este caso, la Figura 2 muestra un ejemplo del tipo de gráficos que se pueden generar en ViSta y su posible utilidad como complemento en el cálculo del TE. Dicha figura presenta diferentes imágenes de un gráfico de puntos, diamantes y cajas (dot, diamond and box plot). La primera imagen (arriba a la izquierda) muestra el gráfico de puntos -representando los participantes de cada grupo- y las medias de ambos grupos unidas por una línea. Este gráfico permite apreciar la diferencia entre las medias y también visualizar un aparente outlier o caso atípico en el grupo control. El segundo gráfico (arriba a la derecha) es un esquema de las distribuciones basado en las medias y desvíos estándar de cada grupo. Se añaden al gráfico anterior dos diamantes como indicadores de la variabilidad de los grupos. Aquí, los extremos de cada diamante se fijan en un desvío por encima y por debajo de la media de cada grupo. El tercer gráfico (abajo a la izquierda) también es un esquema de las distribuciones, aunque éste se basa en medidas de posición. Se trata de un gráfico de cajas (box plot) donde la línea central corresponde a la mediana, las cajas están definidas por los cuartiles uno y tres, y las líneas de los extremos representan los percentiles 10 y 90, respectivamente. Por último, el gráfico ubicado abajo a la derecha es una superposición de todos los anteriores.
La información gráfica anterior sugiere la existencia de una diferencia entre las medias a favor del grupo experimental, pero también permite detectar cierta heterogeneidad en las varianzas y un aparente outlier en el grupo control, cuestiones que se deben tener en cuenta al momento de la comparación. Considerando que el outlier puede afectar la media del grupo control y contribuir a la heterogeneidad de las varianzas, el analista podría razonablemente estar interesado en realizar el análisis nuevamente, eliminando el outlier de los datos. La eliminación de casos atípicos se justifica, en ocasiones, por el incumplimiento de criterios de inclusión en el reclutamiento de los participantes que conforman la muestra, o bien por errores en el ingreso de datos (Miller, 1993). Este tipo de operaciones (selección, eliminación de participantes, etc.) puede realizarse de modo sencillo en ViSta utilizando un Panel de Selección. Así, la aplicación de los análisis, en este caso el cálculo del TE, resulta más dinámica e interactiva para el usuario.
La Tabla 4 muestra los resultados del análisis luego de proceder con dicha eliminación. Se observan cambios en las estimaciones del TE, así como un resultado más satisfactorio en el Test de homogeneidad de varianzas. En síntesis, el ejemplo permite ilustrar que el TE puede calcularse de modo sencillo en ViSta, con la ventaja añadida de que el usuario también pude interactuar con el resto de las opciones del programa, tales como obtener salidas gráficas, seleccionar o eliminar participantes, etc.
COMENTARIOS FINALES
El TE se ha planteado como un complemento necesario a las pruebas de hipótesis (Cohen, 1988). El TE permite una apreciación más directa de la magnitud de los fenómenos en estudio y ofrece una interpretación más adecuada de los resultados. Además, resulta un elemento necesario para la integración de diversos resultados mediante el Meta-Análisis (Hunter & Schmidt, 2004; Macbeth et al., en prensa). De ahí las recomendaciones de los expertos y de las normas editoriales de las revistas especializadas que promueven con un énfasis creciente el empleo de estas técnicas.
No obstante, su uso se encuentra aún poco extendido en la práctica, lo cual podría explicarse, en parte, por desconocimiento y, en parte, porque los programas estadísticos más populares no lo incluyen claramente entre sus opciones de análisis. Es curioso, por ejemplo, que muchos manuales de estadística en Psicología no incorporen este tema entre sus contenidos básicos siendo que su cálculo e interpretación resultan relativamente sencillos. Aquí puede verse, también el énfasis en las pruebas de hipótesis y los valores de significación tradicionales de 0,01 y 0,05.
En este contexto, el presente trabajo intenta contribuir a los esfuerzos realizados por instituciones como la APA por difundir y animar el uso del TE entre los investigadores en Psicología. Con tal propósito, se proporciona aquí una implementación informática simple de usar y de libre acceso, que se acopla al programa estadístico ViSta.
En cuanto a la disponibilidad y funcionamiento de esta implementación informática, el usuario interesado simplemente debe: a) Instalar la versión 6.4 de ViSta, y b) Instalar el programa ViSta-ES, que añade las opciones de estimación del TE en ViSta. Ambos programas pueden encontrarse en la dirección URL: http://www.mdp.edu.ar/psicologia/vista/Por último, quienes estén interesados en una revisión general de las capacidades y funcionamiento de ViSta pueden consultar a Molina-Ibañez, Ledesma, Valero-Mora y Young (2005).REFERENCIAS
Anderson, G. (1999). The Role of Meta-Analysis in the Significance Test Controversy. European Psychologist, 4(2), 75-82. [ Links ]
Cohen, J. (1988). Statistical Power Analysis for the Behavioral Sciences. Second Edition. Hillsdate, NJ: LEA. [ Links ]
Cohen, J. (1990). Things I Have Learned (So Far). American Psychologist, 45(12), 1304-1312. [ Links ]
Cohen, J. (1992a). A Power Primer. Psychological Bulletin, 112(1), 155-159. [ Links ]
Cohen, J. (1992b). Fuzzy Methodology. Psychological Bulletin, 112(3), 409-410. [ Links ]
Cohen, J. (1994). The Earth Is Round (p<.05). American Psychologist, 49(12), 997-1003. [ Links ]
Kohan, N. (1994). Diseño Estadístico. Buenos Aires: Eudeba. [ Links ]
Kohan, N. (2006). El Tamaño del Efecto en la Investigación Psicológica. Ponencia presentada en el Primer Encuentro de Evaluación Psicológica y Educativa. Córdoba: Universidad Nacional de Córdoba. [ Links ]
Kohan, N. & Macbeth, G. (en prensa). El Tamaño del Efecto en la Investigación Psicológica. Revista de Psicología UCA. [ Links ]
Cortina, J.M. & Dunlap, W.P. (1997). On the Logic and Purpose of Significance Testing. Psychological Methods, 2(2), 161-172. [ Links ]
Gigerenzer, G. (1993). The Superego, the Ego, and the Id in Statistical Reasoning. En G. Keren & C. Lewis (Eds.), A Handbook forData Analysis in the Behavioral Sciences: Methodological Issues (pp. 311-339). Hillsdale, NJ: LEA. [ Links ]
Glass, G.V., McGaw, B. & Smith, M.L. (1981). Meta-Analysis in Social Research. Thousand Oaks, CA: Sage. [ Links ]
Grissom, R.J. & Kim, J.J. (2005). Effect Sizes for Research. A Broad Practical Approach. Mahwah, NJ: LEA. [ Links ]
Hunter, J.E. & Schmidt, F.L. (2004). Methods of Meta-Analysis. Correcting Error and Bias in Research Findings. Second Edition. Thousand Oaks, CA: Sage. [ Links ]
Krueger, J. (2001). Null Hypothesis Significance Testing. On the Survival of a Flawed Method. American Psychologist, 56(1), 16-26. [ Links ]
Kohan, N. & Razumiejczyk, E. (en prensa). El Meta-Análisis: la Integración de los Resultados Científicos. Evaluar. [ Links ]
McGraw, K. y Wong, S. (1992). A common language effect size statistic. Psychological Bulletin, 111, 361-365. [ Links ]
Miller, J.N. (1993). Outliers in Experimental Data and Their Treatment. Analyst, 118, 455-46. [ Links ]
Molina-Ibañez, J.G., Ledesma, R., Valero-Mora, P. & Young, F.W. (2005). A Video Tour through ViSta 6.4, a Visual Statistical System based on Lisp-Stat. Journal of Statistical Software, 13(8), 1-10. [ Links ]
Moore, D.S. & McCabe, G.P. (1993). Introduction to the Practice of Statistics. Second Edition. New York: W.H. Freeman & Company. [ Links ]
Thompson, B. (1998). Statistical Significance and Effect Size Reporting: Portrait of a Possible Future. Research in the Schools, 5(2), 33-38. [ Links ]
Tierney, L. (1990). Lisp-Stat An Object-Oriented Environment for Statistical Computing and Dynamic Graphics. NY: John Wiley & Sons. [ Links ]
Valera-Espín, A. y Sánchez-Meca, J. (1997) Pruebas de significación y magnitud del efecto: Reflexiones y propuestas. Anales de psicología, 13, 1, 85-90 [ Links ]
Young, F.W. (1996). ViSta: The Visual Statistics System. UNC L.L. Thurstone Psychometric Laboratory, Research Memorandum 94-1. [ Links ]
Recibido: Abril de 2007
Aceptación final: Octubre de 2008