SELECCIONES

De Pearson a Spearman

From Pearson to Spearman


Luis F Restrepo B^1*, Estad, Esp estad bioma; Julián González L², Esp Est, Esp Bioma, MS.

¹ Grupo Grica, Facultad de Ciencias Agrarias Universidad de Antioquia, Medellín, Colombia. ² Profesor Titular Universidad de Caldas, Facultad de Ciencias Exactas y Naturales, Manizales, Colombia.
lusitano@agronica.udea.edu.co

(Recibido: 5 octubre, 2005; aceptado: 26 abril, 2007).


Resumen

Este artículo trata acerca de los coeficientes de correlación de Pearson y Spearman los cuales son ampliamente utilizados en las ciencias agropecuarias con el fin de establecer relaciones entre variables generalmente de índole cuantitativo. Además contiene los supuestos fundamentales en los que se basa el método de Pearson: normalidad bivariada, linealidad en la interacción de las variables y la forma de programación en el paquete estadístico SAS; adicionalmente, la manera de interpretar las salidas derivadas del paquete estadístico las cuales oscilan entre -1 ≤ ρ ≤ 1.

Palabras clave: coeficiente, correlación, supuestos.


Summary

This article is about the Pearson and Spearman correlation coefficients which are widely used in agricultural sciences in order to establish the relationships between generally quantitative variables. It also contains the fundamental assumptions in which the Pearson method is based: bivariated normality, variable interaction linearity, as well as the programming Schedule in SAS software; in addition, the way in which SAS exits must be interpreted which oscillate between -1 ≤ ρ ≤ 1.

Key words: assumptions, coefficient, correlation.

* Autor para el envío de la correspondencia y la solicitud de separatas. Facultad de Ciencias Agrarias, Universidad de Antioquia, AA 1226, Medellín, Colombia. E-mail: lusitano@agronica.udea.edu.co


Introducción

Los métodos de correlación de Pearson y la información derivadas de análisis matriciales Spearman son técnicas bivariadas que se emplean con propiedades del álgebra lineal, que permiten en el campo multivariado, en situaciones donde el establecer similaridades o disimilaridades entre las variables e individuos representados en dimensiones de menor valor, generalmente en planos o cubos (segunda y tercera dimensión) para esclarecer la variabilidad conjunta expresada en factores ortogonales que permiten tipificar lo que sucede con los datos. Un ejemplo particular es el referido al investigador en avicultura que podría mediante análisis de componentes principales por la técnica R proyectar todas las variables de índole cuantitativo relacionadas con el huevo, a fin de determinar la participación de cada variable dentro del factor abstracto que él debe discernir para poder comprender mejor lo que sucede con los aspectos morfométricos y de composición. También puede centrar su interés mediante análisis canónicos para evaluar las variables preponderantes en la morfometría del ave con relación a las variables tomadas en el huevo, y así conocer las incidencias particulares y colectivas de los factores sujetos en el estudio.

La técnica de correlación es fundamental en la explicación de muchos fenómenos relacionados con el campo animal y vegetal. A modo de ejemplo, se puede citar el interés que pueda tener el ganadero en relacionar la ganancia de peso con el consumo de alimento; la condición corporal con la incidencia de las variables climáticas; el intervalo entre partos con el número de partos, entre muchas otras variables.

En el campo de la ingeniería acuícola es de interés relacionar aspectos de la morfometría del pez asociada con las variables longitud estándar, ancho del cuerpo, longitud de la cabeza, altura de la cabeza, altura del opérculo, diámetro de los ojos, longitud cobertura ocular, apertura de la boca, grosor del labio, longitud base aleta dorsal, altura aleta dorsal, distancia aleta dorsal adiposa, longitud base aleta dorsal, longitud preanal, longitud aleta pélvica y la longitud aleta pectoral entre otras, con respecto a condiciones ambientales y de alimentación.

El experto en apicultura podría estar interesado en ver la asociación entre la producción de miel con respecto al tiempo que tarda la abeja en lograr extraer el polen de la flor, el tipo de flor y su edad vegetativa, las condiciones climáticas predominantes en el lugar de evaluación, la macro y micro fauna presentes.

El ingeniero agrónomo puede mediante las técnicas de correlación establecer patrones de asociación entre las variables del suelo representadas en elementos mayores o menores, con respecto al desarrollo de un cultivo. En el caso particular de pastos y forrajes, se podría evaluar la asociación entre las condiciones físico químicas del pasto y la producción de carne o leche de un hato en particular.

El experto en clínica veterinaria puede en un momento dado relacionar la cantidad suministrada de un fármaco para anestesiar a un animal y su correlación con el pulso cardiáco, la edad, la condición corporal y el peso del canino entre otras variables de interés.

En nutrición animal se puede asociar la cantidad de alimento suministrada cuando se elabora un bloque nutricional como suplemento con respecto a la conversión y ganancia de peso en las distintas etapas del proceso de desarrollo del animal.

Cuando se trabaja con fauna silvestre se mide la presencia o ausencia de determinada especie en relación a las variables ambientales presentes y dominantes en un ecosistema, además se evalúan las variables morfométricas y ambientales para establecer patrones que permitan evaluar la factibilidad de la especie para subsistir en el medio.

En avicultura se puede asociar el peso del huevo en relación a la cantidad de alimento suministrada, la edad del ave, la longitud del ovioducto, la cantidad de agua tomada por las aves, densidad del galpón, humedad relativa, temperaturas máxima y mínima.

En el cultivo del banano mediante las técnicas de correlación se puede medir la intensidad de la relación de las variables precipitación, temperatura, velocidad del viento, humedad relativa, con la altura de la planta, grosor del fruto, longitud del fruto, porcentaje de pérdida, calidad del fruto; además, se pueden asociar elementos del suelo como nitrógeno, fósforo, potasio y algunos elementos menores.

En general son múltiples los casos particulares donde las técnicas de correlación son ampliamente utilizadas, no sólo para evaluar el grado de dependencia entre ellas, sino también para ver la bondad de ajuste de los modelos de serie de tiempo en la evaluación de las auto correlaciones y en la convalidación de algunos supuestos.

Coeficiente de correlación

Un coeficiente de correlación, mide el grado de relación o asociación existente generalmente entre dos variables aleatorias. No es conveniente identificar correlación con dependencia causal, ya que, si hay una semejanza formal entre ambos conceptos, no puede deducirse de esto que sean análogos (9, 15); en efecto es posible que haya una alta correlación entre dos acontecimientos y que sin embargo, no exista entre ellos relación de causa o efecto; por ejemplo cuando dos acontecimientos tienen alguna causa común, pueden resultar altamente asociados y no son el uno causa del otro. Cabe recordar que el coeficiente fluctúa entre -1 ≤ ρ ≤ 1.

En un estudio médico se estableció que al comparar el consumo de carbón con la mortalidad, en periodos análogos, se encontró alta correlación. Esto no quiere decir que el consumo de carbón sea la causa de las muertes, sino que tanto el aumento de consumo de carbón, como el aumento de la mortalidad se producen en las épocas de frío más intenso. En conclusión, un coeficiente de correlación por sí mismo no puede probar ni desmentir una relación causal entre variables. La relación causa – efecto es posible definirla sólo a través de la comprensión de la relación natural que exista entre las variable y esto no debe manifestarse sólo por la existencia de una fuerte asociación. El análisis de correlación es técnicamente neutral (7, 12, 13).

Coeficiente de correlación de Pearson

Tiene como objetivo medir la fuerza o grado de asociación entre dos variables aleatorias cuantitativas que poseen una distribución normal bivariada conjunta. El coeficiente se define por la siguiente fórmula (14):

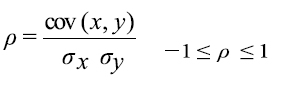
Cuando ρ=+ la relación es directa entre las variables. Si ρ=- la relación es inversa y si ρ= 0 son independientes. Dicho coeficiente se puede expresar en términos de su estadístico como (8):




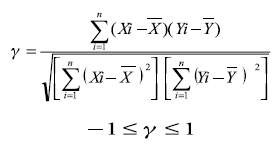
El coeficiente de correlación de Pearson es la media geométrica entre las pendientes de los modelos de regresión lineal simple Y/X, X/Y así:
y _i = β _o + β₁ X_i + ε_i


Donde:

βo = intercepto del modelo.
^β1= pendiente del modelo, cambio esperado en y por unidad de cambio en x.



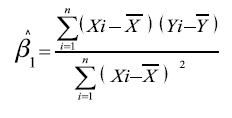
Por el método de los mínimos cuadrados ordinarios



Supuestos que fundamentan al coeficiente de correlación:

1. La distribución conjunta de las variables (X, Y) debe ser normal bivariada (8), y corresponde a:



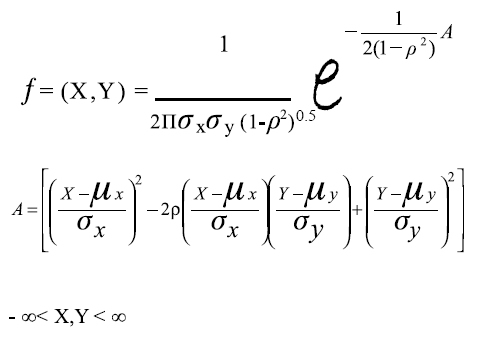
2. En términos prácticos para validar dicho supuesto se debe observar que cada variable se distribuya en forma normal (11, 15), si una sola de las variables se desvía de la normalidad, tampoco es normal la distribución conjunta.
3. Debe existir una relación de tipo lineal entre las variables (X, Y).
4. Para cada valor de X, hay una subpoblación de valores de Y normalmente distribuidas.
5. Las subpoblaciones de valores Y tienen varianza constante.
6. Los promedios de las subpoblaciones de Y tienen ubicación en la misma línea recta.
7. Las subpoblaciones de X tienen varianza constante.
8. Las medias de las subpoblaciones de X se encuentran en la misma línea recta.
9. Para cada valor de Y hay una subpoblación de valores X que están normalmente distribuidas (18).

Prueba de hipótesis

Bajo la hipótesis Ho: ρ =0



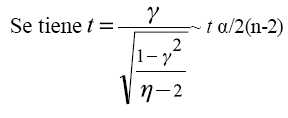
Si se desea contrastar

Ho: ρ = ρo hipótesis nula,
H₁: ρ ≠ ρo hipótesis alternativa

Se debe aplicar la estadística:




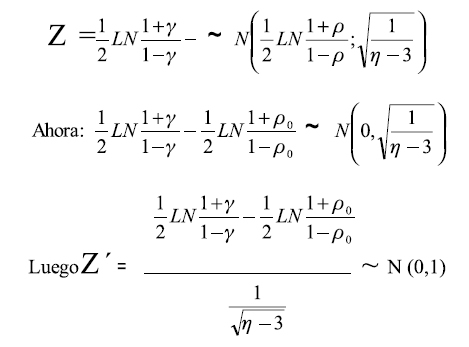
Si 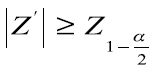se rechaza Ho, se acepta H_1,hay relación estadística entre las variable. Si se acepta Ho las variables son independientes.

Cabe anotar que el coeficiente de correlación de pearson puede ser empleado utilizando un factor de ponderación Wi, el cual efectúa un ajuste a la media aritmética y por ende al coeficiente de asociación. Esta ponderación se debe aplicar, cuando el investigador quiera darle un peso específico a cada individuo que interviene en el estudio.

Cuando una variable es dicotómica y la otra continua, el coeficiente de correlación de pearson es igual al biseral puntual, si ambas variables son dicotómicas, Pearson es igual al coeficiente phi (φ).

El coeficiente de correlación de pearson no se debe extrapolar más allá del rango de los valores observados cuando se efectúa inferencia. Para construir el intervalo de confianza asociado con Pearson, ambas variables se deben distribuir en forma normal y para predecir se utiliza la técnica propuesta por Rubens (16).


Aplicación

Se evaluaron 44 ejemplares de trucha en un estudio de índole acuícola, con el fin de relacionar la longitud del cuerpo y su ancho. En la salida de la figura 1, se muestra el coeficiente de correlación de los datos fueron suministrados por un docente del Pearson y los supuestos asociados a la técnica, donde área.



Interpretación

Al observar el valor p de prueba asociado con el estadístico de Pearson se aprecia relación entre la longitud y ancho dado que p<0.05; cabe anotar que el supuesto de normalidad bivariada no se cumplió debido a que la variable ancho no se ajusta a la distribución gaussiana o normal como se aprecia en las pruebas de normalidad de Shapiro-Wilk, Kolmogorov-Smirnov, Cramer-von Mises, Anderson- Darling donde el p<0.05. La figura 2 muestra una tendencia lineal.





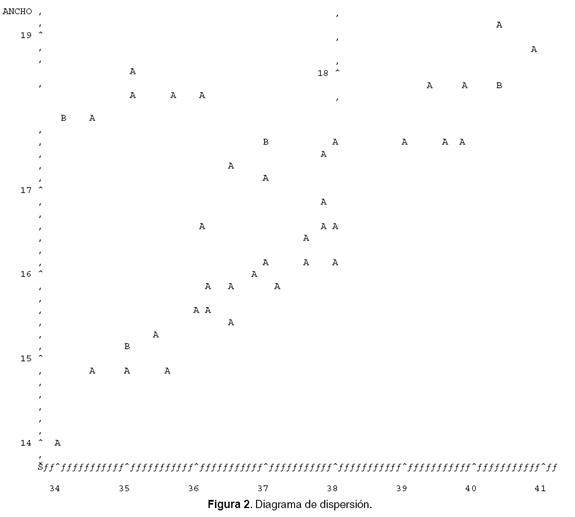
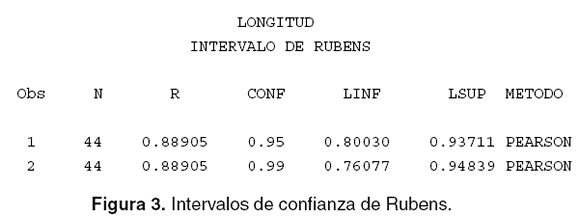
Lo anterior indica que con un 95% de confiabilidad el coeficiente de correlación fluctúa entre 0.80030 y 0.93711

Coeficiente de correlación de Spearman es un coeficiente no paramétrico alternativo al coeficiente de correlación de Pearson cuando este no cumple los supuestos (3, 4, 19). Charles Spearman contribuyó al análisis del factor, a la teoría de la inteligencia, elaboró una prueba de la teoría mental (17).

Se define el coeficiente de correlación de rangos de Spearman como el coeficiente de correlación lineal entre los rangos Ri (x) y Ri (y), en la fórmula de Pearson se reemplaza Xi por Ri(x) y Yi por Ri (y) quedando:


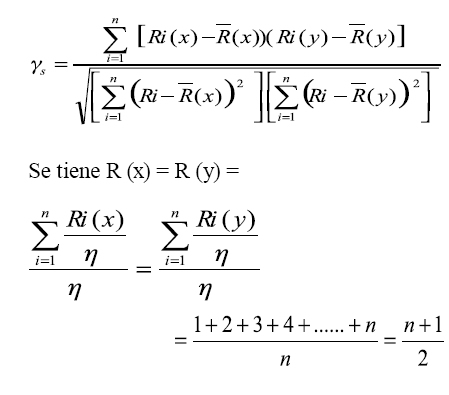
Por la propiedad telescópica

Ahora:



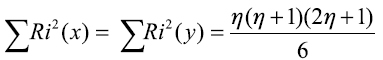
por la misma propiedad citada anteriormente.



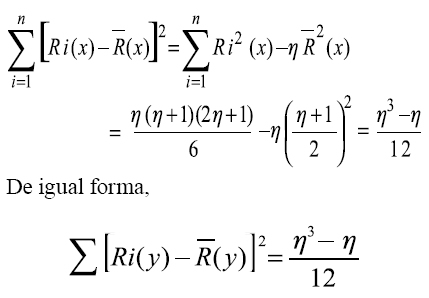
Definamos di = Ri(x)- Ri(y) esto es la diferencia de rangos entre las variables.


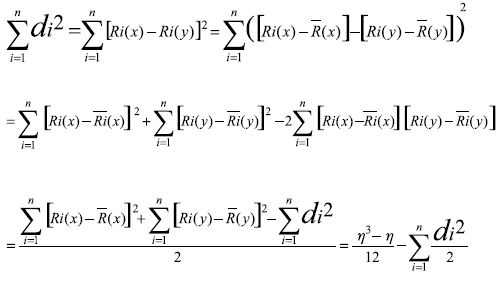
Por lo tanto el coeficiente de correlación de Spearman resulta como:



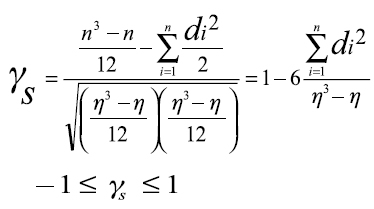
La asociación crítica del contraste la formarán valores de Y_S próximos a 1 o a –1 determinándose a partir de la relación:



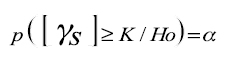
Cuando n ≥ 10 se debe emplear la distribución asintótica propuesta por Kendall dada a través de la variable aleatoria




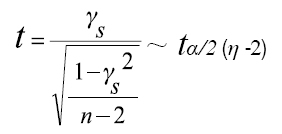
Cuando aparecen datos repetidos en la variable aleatoria X o Y se recomienda aplicar la fórmula:



Tx′ se define como el número de veces que se repite un valor en la variable X, igual definición para Y

Y_s mide la tendencia de X, Y a relacionarse en forma monótona creciente o decreciente. Al medir el grado de asociación de forma monótona entre las variables X, Y, Y_s no se encuentra restringido a descubrir sólo una asociación lineal entre las variables.

Ventajas del coeficiente de Spearman

1. Al ser Spearman una técnica no paramétrica es libre de distribución probabilística (2, 5, 9).

2. Los supuestos son menos estrictos. Es robusto a la presencia de outliers (es decir permite ciertos desvíos del patrón normal). La manifestación de una relación causa-efecto es posible sólo a través de la comprensión de la relación natural que existe entre las variable y no debe manifestarse sólo por la existencia de una fuerte correlación (1, 5).

Ejemplo

Con base en la información de las 44 truchas y ante el no cumplimiento de los supuestos del coeficiente de correlación de Pearson se aplicó la técnica no paramétrica de Spearman dando como resultado la siguiente salida (véase Figura 4).




Se encontró relación directa entre la longitud y el ancho del pez ya que el p<0.05




Con un 95% se estima que el coeficiente oscila entre 0.81378 y 0.94167

Procedimiento SAS para establecer los coeficientes de correlación de pearson validando supuestos:



La correlación fue utilizada por primera vez por Francis Galton, aunque su discípulo Karl Pearson fue quien estudió en profundidad sus propiedades. La correlación de rangos fue introducida por el psicólogo Charles Edward Spearman al intentar construir una teoría de la inteligencia (10, 14, 17).

Los coeficientes de correlación de Pearson y Spearman

Estos coeficientes también son apropiados para evaluar la relación entre variables ordinales representadas en tablas de contingencia.

El coeficiente de correlación de Pearson se define:





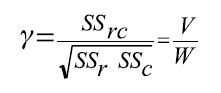
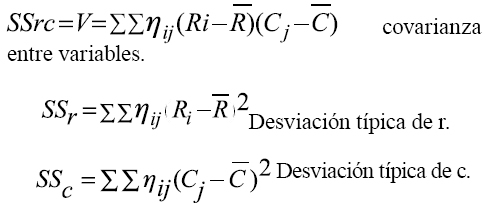
Ri , C_j representan los valores referidos a las filas y a la columna

Para probar el coeficiente de correlación de Pearson asintóticamente, se elabora una prueba estadística estandarizada Y^* bajo la hipótesis nula de que el coeficiente de correlación es igual a cero.




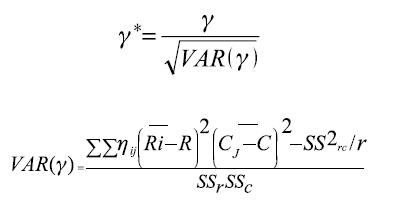
La varianza asintótica es derivada de una muestra con distribución multinomial representada en una tabla de contingencia.

El coeficiente de correlación de Spearman se define:



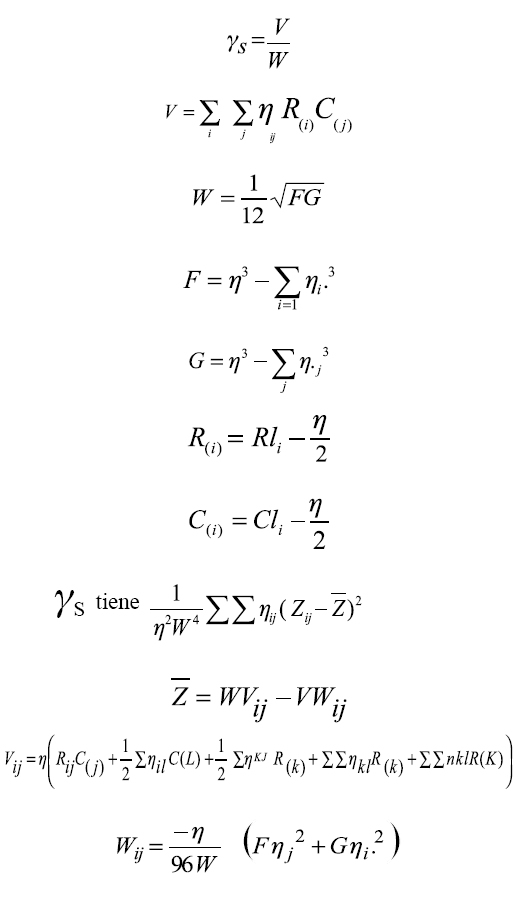
Para efectuar la prueba asintótica para el coeficiente de correlación de Spearman se usa γs* el cual se define:



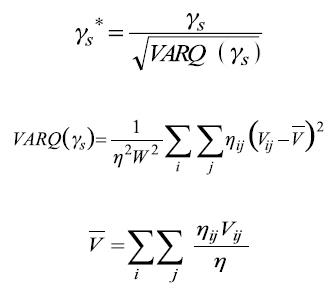
La varianza es derivada de una distribución multinomial referida a una tabla de contingencia.

El procedimiento SAS para encontrar el coeficiente de correlación de Pearson y Spearman referido a tablas de contingencia es:




Referencias

1. Altman DG. Practical statistics for medical research, C and Hall London, 1991. 611p.         [ Links ]

2. Bartholomew DJ. Spearman and the origin and developmend of test theory. British J Mat Stat Psychol 1995; 48:211-220.         [ Links ]

3. Burt C. Experimental test of general Inteligence. British J Psychol 1909; 3:94-177.         [ Links ]

4. Cattell R B, Spearman CE. International encyclopedia of the social sciences , D.E Sills ed New York, 1968; 15:108-111.         [ Links ]

5. Conover WJ, Practical nonparametric statistical 3ra ed New York, John Wiley, 1998. 578p.         [ Links ]

6. Dallas E. Métodos multivariados aplicados al análisis de datos. International Thomson Editores. Mexico, D.F. 2000. 566p.         [ Links ]

7. Dawin-Saunders B, Trapp RG. Bioestadística Medica. 2da ed México, el Manual Moderno, 1996. 86p.         [ Links ]

8. Fanavos C. Probabilidad y Estadística Aplicaciones y Métodos. Editorial MCgraw-Hill. Mexico, D.F. 1988. 651p.         [ Links ]

9. Joe H. Multivariate models and dependence concepsts. Chapman and Hall/CRC, Boca Ralton. New York, 1997. 395p.         [ Links ]

10. Levy P, Spearman`s C. Contribution to Test Theory. J Roy Statl Soc 1995; 48:221-235.         [ Links ]

11. Looney SW, TR Jr . Use of the correlation coefficient with normal probability plots. J Roy Stat Soc 1985; 39:75-79.         [ Links ]

12. Martín AA, Luna JD. Bioestadística para las ciencias de la salud, 4ta ed Madrid, Norma, 1993. 114p.         [ Links ]

13. Milton JS, Toscos JO. Estadística para biología y ciencias de la salud, interamericana Mcgraw- Hill Madrid, 2001. 186p.         [ Links ]

14. Ostle B. Estadística aplicada, editorial científico técnica. Mexico D.F, 1980. 629p.         [ Links ]

15. Pita FS. Correlación frente a la Causalidad. JANO 1996; 4:59-260.         [ Links ]

16. Ruben H. Some new results on the distribution of the sample correlation coefficients. J Roy Stat Soc 1966.         [ Links ]

17. Spearman CE. General inteligence objetictively determined and measured. Am J Psicol 1909; 15:201-293.         [ Links ]

18. Wayne WD, Estadística con aplicaciones a las ciencias sociales y a la educación, Mcgraw-Hill. Mexico, D.F, 1990. 504p.         [ Links ]

19. Zimymerman DW, Williams RH. Properties of the Spearman correction for attnuation for normal and realistic non-normal distributions. Appl Psychol Measurm 1997; 21:253-270.         [ Links ]