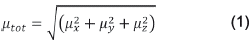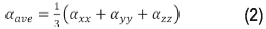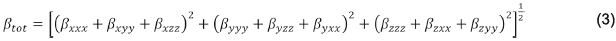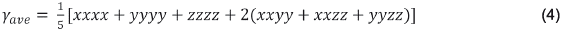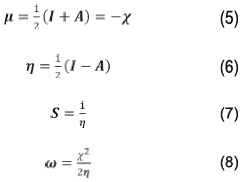Introducción
En los últimos años, parte de la investigación química ha mostrado gran interés en el desarrollo de nuevos materiales con aplicaciones electrónicas y ópticas, desde transistores moleculares hasta celdas solares [1,2]. Los compuestos orgánicos con gran número de insaturaciones conjugadas y sistemas aromáticos han llamado la atención en el diseño de moléculas candidatas para materiales en estos dispositivos. Los métodos de la química computacional han demostrado ser una herramienta poderosa y eficiente para la evaluación de las propiedades moleculares y electrónicas de los posibles candidatos a materiales para optoelectrónica [3-5]. La comparación de la fuerza donadora y aceptora de densidad electrónica de los sustituyentes, grado de conjugación, propiedades espectroscópicas y de óptica no lineal permiten el establecimiento de relaciones de estructura-propiedad que facilitan la exploración virtual de muchas moléculas [6,7]. Este enfoque es importante en el campo tecnológico y ambiental, debido al ahorro de tiempo y recursos en la exploración en la diversidad molecular, además de los retos que puede representar la síntesis de esos candidatos.
Los derivados de pirazol se han destacado en este campo, por ejemplo, Gondek reportó el uso de un derivado de pirazol como aceptor en la heteroestructura de una celda solar [8]. Asimismo, Amudha et al. observaron un incremento en la conductividad y eficiencia en la conversión de energía en una celda solar de polimetilmetracrilato y fluoruro de polivinilideno al doparla con pirazol [9]. A pesar de estos hallazgos, hasta donde se tiene conocimiento, no existen trabajos que describan las propiedades moleculares, espectroscópicas (IR, RMN, UV-vis) y electrónicas para este tipo de compuestos. Sobre esta base, en este trabajo se presenta la descripción y caracterización de la estructura molecular y electrónica de 1,3,5-trifenilpirazol. La discusión consiste en una evaluación detallada de los orbitales moleculares de frontera (HOMO, HOMO-1, LUMO y LUMO+1), las propiedades de óptica no lineal (ONL), electronegatividad (χ), dureza (η), suavidad (S), análisis de población natural (NPA), el mapa de potencial electrostático (MEP) y los descriptores de reactividad global y local (funciones de Fukui).
Teoría
El mapa de potencial electrostático (MEP) es un método de cartografía del potencial electrostático, es decir, muestra la distribución de carga del sistema. Con esta superficie es posible determinar la forma, el tamaño y la orientación del momento dipolar de la molécula, representando un método visual para comprender la polaridad relativa [10-12]. Adicionalmente, es posible dilucidar cómo las moléculas interactúan entre sí. Los orbitales de frontera, HOMO y LUMO, según la teoría de Fukui, determinan la reactividad de una molécula frente a otra especie [13]. Los orbitales HOMO-1 y LUMO+1 se denominan donante y aceptor, son niveles de energía que se encuentran por debajo y por encima de los niveles principales, respectivamente [14].
La polarización molecular obtenida por la perturbación de un campo electromagnético (F) se expresa como una serie de Taylor en potencias de F. Cada uno de los coeficientes de la serie representa una respuesta particular del sistema. Truncando la serie en el tercer término, definimos el primero como el momento dipolar (μ), el segundo se denomina polarizabilidad molecular (α) y el tercero se conoce como primera hiperpolarizabilidad (β). Cada uno de estos se representa como un tensor; sin embargo, es posible obtener propiedades que son invariantes al sistema de coordenadas partiendo de los elementos de cada tensor. Estas propiedades son susceptibles de ser comparadas un tercio de la traza del tensor de polarizabilidad: con los diferentes experimentos. En este sentido, el momento dipolar total se define como el módulo a del vector momento dipolar:
La polarizabilidad promedio α ave , se define como un tercio de la traza del tensor de polarizabilidad:
En el caso de la primera hiperpolarizabilidad β, se (1) define un vector β (βv), donde cada componente de este vector se calcula como β i=β iii+β ijj+β ikk , ∀ i,j,k ={x,y,z}. En consecuencia, el βtot, o módulo βv, es:
Esta última propiedad está asociada con la transferencia de carga resultante del movimiento de la nube de electrones a través de la estructura conjugada π, la cual va en dirección del grupo donante de electrones al grupo aceptor de electrones 15]. La segunda hiperpolarizabilidad responsable de efectos ONL de tercer orden se calcula utilizando la siguiente expresión:
Las moléculas con un gran momento dipolar y un medio para cambiar la densidad electrónica tendrán hiperpolarizabilidades grandes. En general se puede afirmar que dicha propiedad depende de la fuerza de los grupos dador y aceptor, así como de la longitud de la conjugación en el sistema que los une, por otra parte, en sistemas con anillos aromáticos sustituidos la planaridad afecta e influye en el tamaño del sistema de electrones n y en la movilidad de electrones [16,17].
Por otro lado, propiedades como el potencial químico (μ) y la dureza (η) son expresadas sobre las bases de la aproximación de diferencias Anitas en términos de I y A [18]. La suavidad (S) es un parámetro recíproco de la dureza, (X) corresponde a la electronegatividad (ω), equivale al índice de electrofilicidad; dichos parámetros se expresan en las siguientes ecuaciones:
La función de Fukui se interpreta como el cambio de potencial químico dada una perturbación externa o la variación de la densidad electrónica, y se da al cambiar su número de electrones, ya que cuando el sistema en estudio recibe o cede electrones se define la capacidad electrofílica o nucleofílica de la especie química. La función de Fukui refleja entonces la reactividad de diferentes sitios dentro de una molécula, es decir, la selectividad, en donde la dirección de ataque preferida por un reactivo será aquella donde la función de Fukui presente los valores más altos (19). Por otro lado, la suavidad local se conoce como un indicador para las secuencias de reactividad intermolecular, dado que la suavidad local es una cantidad producto de un descriptor de reactividad global [19].
Metodología
Se utilizó el software Gaussian09 revisión A02 [20] para llevar a cabo los cálculos químico-cuánticos y GaussView 5.08 [21] como visualizador. La optimización de la geometría se realizó al nivel DFT/cam-B-3LYP/6-311++G(d,p) [22] sin restricciones de simetría, y se confirmó la ausencia de autovalores negativos de la matriz hessiana mediante el análisis vibracional. La frecuencia de las vibraciones del espectro IR teórico se corrigieron con un factor de escala de 0,9461 [23-25]. Con esta estructura se realizaron cálculos de energía en conjunto con un análisis de población natural (NPA) para la molécula neutra e ionizada (positiva y negativa) para determinar los centros nucleofílicos, electrofílicos y radicalarios, y obtener posteriormente los descriptores de la reactividad local y las funciones de Fukui nucleofílica y electrofílica condensadas. El espectro UV-Vis y los orbitales de frontera HOMO-1, HOMO, LUMO y LUMO+1 se obtuvieron a partir del cálculo DFT dependiente del tiempo (TDDFT). Las propiedades ópticas lineales y no lineales estáticas, momentos dipolares (μ), polarizabilidad (α), hiperpolarizabilidad de primer orden (β) e hiperpolarizabilidad de segundo orden (γ) se obtuvieron mediante DFT con perturbaciones acopladas (CPDFT). Las ecuaciones (1), (2), (3) y (4) se emplearon para el cálculo de estos parámetros. Los espectros de RMN de 1H y 13C se obtuvieron mediante GIAO, sin considerar acoplamientos spin-spin. Adicionalmente, los desplazamientos se calcularon también con los programas ChemBioDraw [26] y MestReNova [27].
Resultados y discusión
Geometría molecular
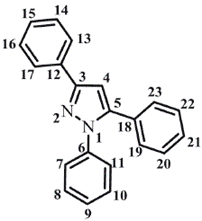
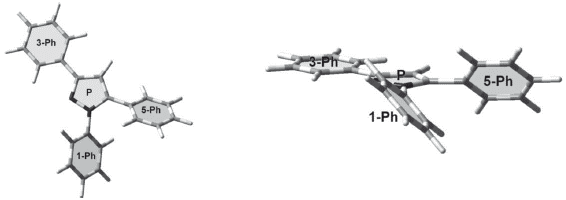
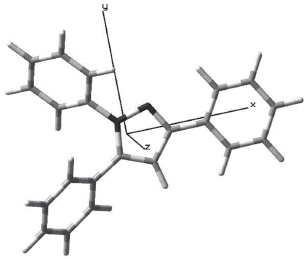
La numeración de los átomos diferentes a hidrógeno usada en la estructura modelada se muestra en la figura 1.
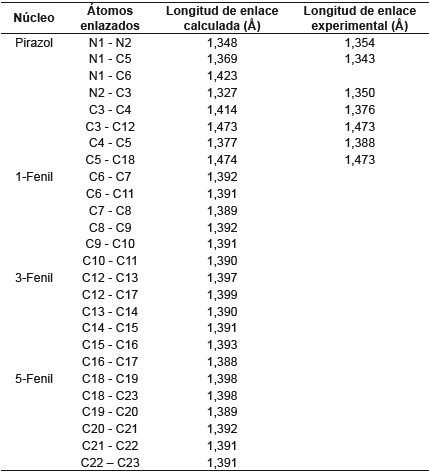
Se conoce que las longitudes de enlace C-C y C-H en el benceno son 1,40 y 1,08, respectivamente [28]. Tomando estos valores como referencia se observa en la tabla 1 que los tres fenilos sustituyentes conservan sus distancias de enlace sin verse modificadas por el anillo de pirazol. Asimismo, se esperaría una modificación en los enlaces de los fenilos sustituyentes en las posiciones 1 y 5 del pirazol, debido a su gran cercanía, pero esto no se presenta, ya que la molécula, al adquirir su geometría de mínima energía, mantiene los parámetros de las longitudes de enlaces.
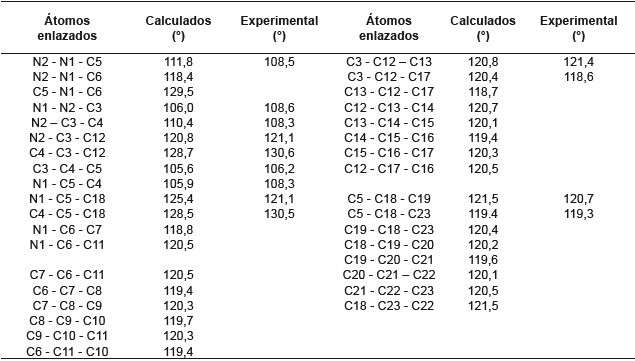
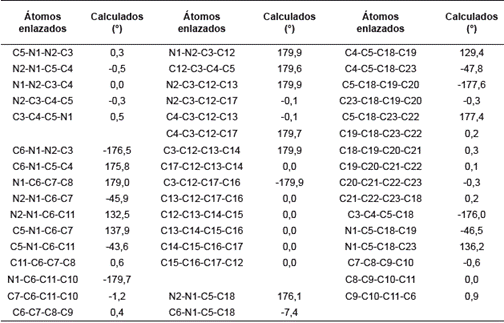
El anillo de pirazol debería ser un pentágono regular con ángulos de 108°, pero debido a la presencia de los dos nitrógenos esta geometría se modifica muy levemente en el ángulo C3-C4-C5 y toma un valor de 106,2°, que es menor al esperado. Comparando los valores experimentales con los calculados se observa que estos últimos presentan mayor distorsión de un pentágono regular, pero aún son muy cercanos. Con respecto a los ángulos de los fenilos sustituyentes y su relación con el anillo de pirazol se observan valores muy cercanos a los esperados de 120° para un hexágono regular. Esto se respalda con los valores experimentales que son muy cercanos a los calculados.
Los valores de los ángulos diedros del pirazol cercanos a cero grados demuestran la planaridad del anillo. Este comportamiento también lo presentan internamente los fenilos que sustituyen el pirazol. La disposición espacial de los fenilos con respecto al pirazol no es coplanar para los 1-Ph (C5-N1-C6-C7= 137,8° y 5-Ph (C4-C5-C18-C19=129,4°. Sólo el 3-Ph (N2-C3-C12-C13= 179,9° presenta coplanaridad con el pirazol (ver figura 2).
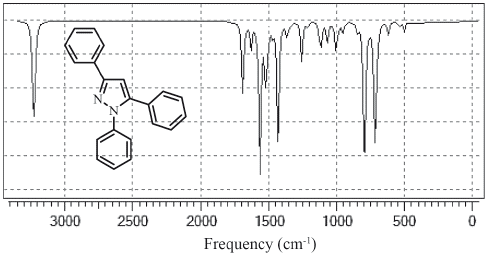
Espectroscopia vibracional
El espectro de IR se presenta en la figura 3. Las vibraciones de C-H para benceno se observan normalmente en el rango de 3000 a 3100 cm-1 [29] con una intensidad media. Las vibraciones calculadas que se muestran en la tabla 4 se correlacionaron bien con los datos experimentales (r2=0,9985). Los estiramientos C=C del benceno generalmente aparecen entre 1400 a 1600 cm-1 [30,31]. En la Tabla 4 se observa que todos los estiramientos experimentales y calculados presentan buena correlación y se encuentran en la región esperada, a excepción de las frecuencias 1363 (1353), 1214 (1283) y 1175 (1190) y 921 (934) que no corresponden a estiramientos en los fenilos y que se atribuyen a las deformaciones y estiramientos del núcleo de pirazol.
Tabla 4 Análisis comparativo de las vibraciones calculadas y experimentales del espectro IR de 1,3,5-trifenilpirazol.
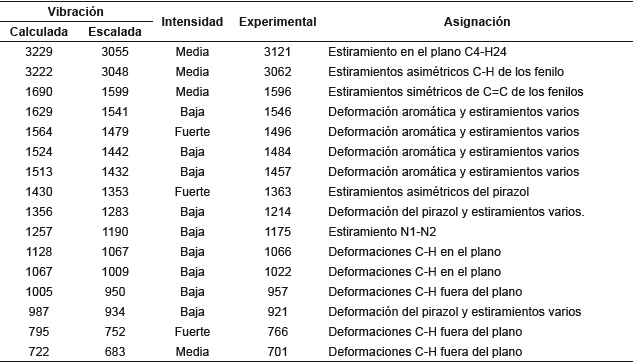
Las deformaciones C-H en el plano se observan entre 1000 a 1300 cm-1 como bandas débiles [30], por lo cual las dos primeras bandas de la tabla 4 muestran estas vibraciones en los anillos de fenilo. A diferencia de esto, las vibraciones C-H fuera del plano se presentan entre 800 a 1000 cm-1 [28], por esto la banda de 957 (950) cm-1 representa este tipo de estiramiento en el fenilo de la posición 3. Asimismo, se presentan dos bandas de 766 (752) y 701 (683) cm-1 que están por debajo de esta región, lo que se atribuye a la cercanía de los fenilos en las posiciones 1 y 5 con los nitrógenos del pirazol. Por último, se observa una banda en 921 (934) cm-1 que se atribuye a la deformación en el plano del pirazol, debido a los estiramientos C3=N2 y C3=C4, los cuales producen que la frecuencia de vibración disminuya y no se observe en la región esperada de 1400 a 3100 cm-1 (31].
Resonancia magnética nuclear (RMN)
Los desplazamientos químicos teóricos de RMN 1H de y RMN 13C de 1,3,5-trifenilpirazol junto con los valores experimentales se presentan en las tablas 5 y 6 [32].
Tabla 5 Comparación de los desplazamientos químicos calculados y experimentales de RMN 1H del compuesto [33,34].
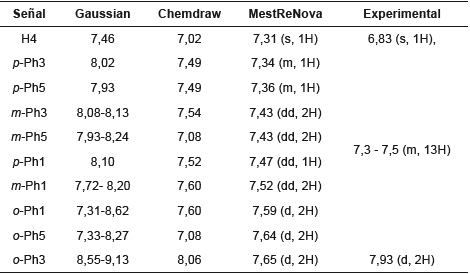
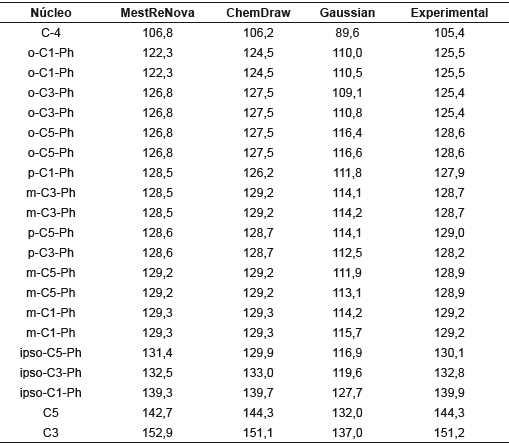
Se observa que los valores de δcal y δexp son cercanos entre sí, especialmente con los programas MestReNova y Chemdraw. Un estudio de correlación lineal mostró que δexp=0,7649δcal+1,3525 con un coeficiente de determinación (r2) igual a 1. El menor valor de δ lo presenta H4, lo cual es coherente con el hecho de que se encuentra rodeado de una gran densidad electrónica proveniente de los fenilos en posiciones 3 y 5. Además, el anillo de pirazol; por ende, necesitará mayor campo para que su spin entre en resonancia. Caso contrario sucede con H30 y H31, que se encuentran más alejados de las nubes electrónicas de los fenilos 1 y 5, por lo que necesita menor campo magnético para entrar en resonancia. En cuanto a los hidrógenos H25 a H29 y H32 a H39, al tener desplazamientos químicos muy cercanos, producen un acoplamiento fuerte que genera un multiplete que integra para 13 hidrógenos, en el cual no se pueden distinguir las señales de cada hidrógeno. La regresión lineal para los desplazamientos químicos calculados y experimentales de RMN 13C muestra una buena correlación entre estos valores (R 2 = 0,966).
C3 y C5 presentan los mayores valores de . Esto es de esperarse, debido a que cada uno está enlazado a un átomo de nitrógeno, el cual, al ser más electronegativo que el carbono, atrae su densidad electrónica, y crea una desprotección y en consecuencia el campo aplicado debe ser menor. Caso contrario sucede con C4, que al estar rodeado por 2 fenilos y la densidad electrónica del pirazol, se necesita un campo aplicado mayor, lo que genera un desplazamiento químico menor.
Espectroscopia electrónica (UV-vis)
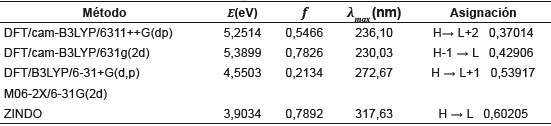
La naturaleza de las transiciones electrónicas, la energía de las transiciones (E), las longitudes de onda de máxima absorción (λ max) y la fuerza oscilatoria (f) para los estados excitados de la molécula fueron calculadas por varios métodos.
A continuación, se presentan la discusión de los resultados obtenidos (tabla 7) para 1,3,5-trifenilpirazol, comparándolos con el dato experimental de 252 nm [37]. En la tabla 8 se presentan los resultados de un estudio comparativo con otros niveles de cálculo.
Tabla 7 Energía, banda de absorción, fuerza del oscilador y transición electrónica de 1,3,5-trifenilpirazol al nivel TD-DFT/cam-B3LYP/6311++G(dp).

Superficie de energía potencial (MEP)
En la figura 4 se ilustran los sitios reactivos de la molécula sobre el anillo 3-Ph y los nitrógenos del pirazol con distribución de carga con los valores de potencial de -5.101 x 10-2 a 5.101 x 10-2. En el resto de la molécula se muestra un color gris tenue que indica que la distribución de electrones en esta zona es neutra o intermedia, es decir, que existe un balance de la densidad electrónica, el cual se da por la presencia de enlaces.
Orbitales de frontera
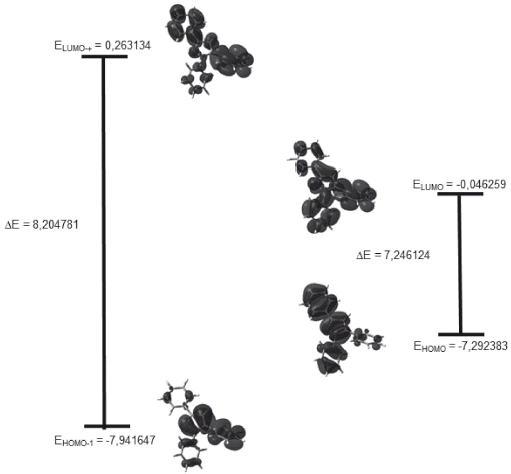
Los valores calculados de energía de los orbitales frontera HOMO-1, HOMO, LUMO y LUMO+1 y band-gap se encuentran tabulados en la tabla 9. La figura 5 muestra que la mayor densidad electrónica de los orbitales HOMO se concentra en la región del anillo de pirazol y el fenilo en posición 3, es decir, en los anillos coplanares, ya que se carece de sustituyentes. Por otro lado, en el orbital LUMO la densidad electrónica está distribuida sobre todo el sistema, pero en especial en la región del pirazol, los fenilos en posiciones 1 y 5, siendo así el orbital HOMO el dador y el orbital LUMO el aceptor. En el HOMO -1 la densidad electrónica se centra en la parte derecha de todo el sistema, es decir, dicha densidad se encuentra concentrada sobre el fenilo en posición 5, por otra parte, en el LUMO +1 la densidad electrónica se encuentra totalmente concentrada en los fragmentos fenilo 3 y 5.
Tabla 9 Valores calculados para los orbitales de frontera y su respectivo band-gap de 1,3,5-trifenilpirazol al nivel de cálculo DFT/cam-B-3LYP/6-311++G(d,p).
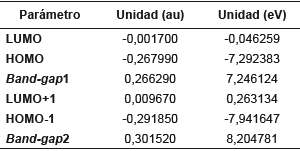
Un band-gap de 7,246124 eV indica claramente que la molécula es muy estable, es decir, la transferencia de la carga está ocurriendo dentro de la molécula mediante el sistema espaciador. El compuesto en estudio no sería un buen candidato para ser utilizado como semiconductor, debido a este alto valor y posiblemente actuaria mejor como resistor 10]. En general los materiales semiconductores orgánicos incluyen hidrocarburos aromáticos policíclicos (HAP) donde las propiedades conductoras dependen de la brecha energética y está establecido que la energía de banda de separación de los aislantes es grande (> 4 eV), pero inferior para semiconductores (< 3 eV) [11]. En el diagrama también se muestra el band-gap entre los orbitales HOMO-1 y LUMO+1 de 8,204781 eV, lo cual indica para que se lleve a cabo una transición de electrones necesitaría mucha energía, al tener este un valor mayor que el bang-gap de los orbitales HOMO-LUMO.
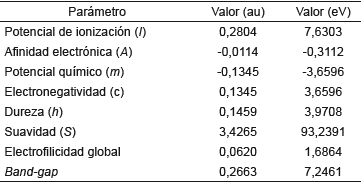
A partir de las energías de los orbitales HOMO y se pueden determinar propiedades como potencial químico, electronegatividad, dureza y suavidad que describen la reactividad global de la molécula [38,39]. El potencial químico está relacionado con la electronegatividad, el cual indica que la densidad electrónica del sistema puede variar y los electrones pueden fluir de una región de alto potencial o mayor electronegatividad a uno de menor potencial o menor electronegatividad. El resultado obtenido para la molécula neutra (-3,6596 eV) nos indica que la densidad electrónica del sistema puede variar espontáneamente, al tener este un valor negativo [40]. Por otro lado, el valor de electronegatividad de 3,6596 eV indica que la molécula tiende a atraer electrones sin cambiar su densidad electrónica. La dureza (η) corresponde a la separación entre el HOMO y LUMO, cuanto mayor es la brecha de energía orbital HOMO-LUMO, más dura es la molécula, lo que indica claramente que si la brecha de energía es mayor, la molécula será más dura, es decir, mide la resistencia impuesta por este al cambio en su distribución electrónica o polarizarse. Por tanto, el sistema, al tener un valor de dureza de 3,9708 eV tendrá poca tendencia a dar o recibir electrones, es decir, la dureza se ha asociado con la estabilidad del sistema químico. En ese orden de ideas y aplicando la teoría de ácidos y bases de Parr y Pearson [41,42], se tiene que el sistema en estudio posee un comportamiento de base dura, caracterizándose por su baja polarizabilidad, alta electronegatividad y por ser una especie donadora de electrones, por tanto, preferirá reaccionar con sistemas que presenten el comportamiento de un ácido duro. La suavidad puede medir el grado de reactividad química del compuesto y esta tiene un valor de 93,2391 eV y es el recíproco de la dureza [43].
Propiedades de óptica no lineal (ONL)
Las componentes vectoriales del momento dipolar calculado fueron μx = -2,5736 D, μy = -0,8183 D y μz = 0,0823 D y el módulo es 2,702 D. La componente tiene la mayor contribución, debido a que ese es el eje que contiene los nitrógenos del anillo de pirazol. La polarizabilidad del sistema de electrones π se logra uniendo grupos electro donadores y electro aceptores al principio y al final de los anillos o sistemas de anillos, con esto se crea un eje de transferencia de carga, por tanto, la polarizabilidad de una molécula es la medida de la capacidad de responder a un campo eléctrico y adquirir un momento eléctrico dipolar. Una sustitución en el fenilo en posición 5 permitiría lograr esta polarización.
Tabla 11 Momento dipolar (μ), polarizabilidad (α) e hiperpolarizabilidad (β) de 1,3,5-trifenilpirazol, urea y p-nitroanilina al nivel de cálculo cam-B3LYP/6-311++G(d,p).
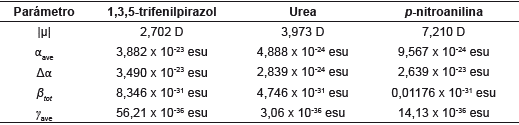
Los valores obtenidos para las polarizabilidades promedios se muestran en la Tabla 11, al igual que el valor de la anisotropía de la polarizabilidad (dependencia de la orientación molecular respecto a un campo eléctrico aplicado) en función de sus tensores (fuerza ejercida sobre una superficie de la molécula) sobre los ejes x, y, z. Los resultados de la polarizabilidad promedio muestran el comportamiento esperado en comparación con la urea y la p-nitroanilina. Se espera que por ser de mayor tamaño, sea mayor su valor. El valor de hiperpolarizabilidad (β) (8,346 x 10-31 esu), 0,746 veces el valor para la urea y 709,6 el de la p-nitroanilina, muestra que el pirazol sería un material con buena respuesta óptica no lineal y posibles aplicaciones optoelectrónicas. Se sugiere que la deslocalización de electrones a lo largo del esqueleto conjugado y la asimetría de la molécula conducen a un aumento de la hiperpolarizabilidad molecular.
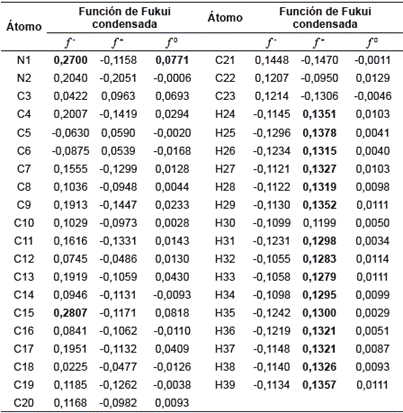
Descriptores locales de reactividad
Las funciones condensadas de Fukui para los estados aniónico (f A -), catiónico (f A +) y radicalario (f A 0) se muestran en la tabla 12. Los valores de las funciones de Fukui negativos no se tendrán en cuenta, ya que no tienen significado físico, puesto que los valores de estas funciones están relacionados con la probabilidad de encontrar un electrón en un orbital, lo que corresponde al cuadrado de la función de onda del sistema, por tanto, nunca se obtendrán valores negativos. Observando los valores de f + en la tabla 12 se tiene que los valores más altos (0,1378-0,1319), los cuales corresponden a los hidrógenos de los fenilos, y les provocan características electrofílicas, lo que los hace susceptibles a un ataque nucleofílico. De igual forma, se puede analizar que el valor más alto de f - lo posee el átomo de C15, con un valor de 0,2807, lo que indica que este es el átomo más susceptible para el ataque de un electrófilo, debido a la alta densidad electrónica del fenilo al cual pertenece. El segundo valor más alto de f corresponde al N1 del pirazol (0,2700), como consecuencia al par electrónico solitario que posee. Siguiendo se tiene que el tercer valor más alto de f - es el C7 con un valor de 0,2777 debido a la alta densidad electrónica del sistema fenil, que hace parte de este anillo, podrían experimentar reacciones de sustitución electrofílica aromática que llevarían a activar la posición para. Otro de los valores más altos de corresponde a N3, con un valor de 0,1975, este nitrógeno había presentado propiedades electrofílicas, pero comparando su f + y f - se encuentra que este último es mucho mayor, lo que indica que este nitrógeno tendrá mayor tendencia a reaccionar con electrófilos, ya que predomina la densidad del carga del sistema π sobre el efecto inductivo.
Debido a que el sistema en estudio es grande, las funciones de Fukui tienden a diluirse entre los átomos y en muchos de los casos su diferencia presenta valores pequeños. Para estos casos se hace uso de otros descriptores locales de reactividad, llamados suavidades locales, los cuales complementan el estudio sobre los puntos más reactivos en la molécula. La suavidad local es directamente proporcional a la función de Fukui, por tanto, en este caso los valores más altos en los tres parámetros los poseen los mismos átomos.
Conclusiones
En el presente trabajo, la estructura molecular optimizada del conformador estable, las propiedades vibratorias y electrónicas del 1,3,5-trifenilpirazol han sido calculadas por el método DFT/cam-B3LYP/6-311++G(d,p). Los parámetros geométricos optimizados (longitudes de enlace y ángulos de enlace) se determinan teóricamente y se comparan con los resultados experimentales. Las propiedades espectroscópicas de la presente molécula se examinaron mediante cálculos de frecuencia al mismo nivel y se compararon con los datos experimentales. Las asignaciones vibratorias de los números de onda se realizaron usando GausView 5. Las propiedades electrónicas también se calcularon con diferentes métodos para determinar el espectro UV-Vis. Las energías de MO y la λ max del compuesto también se evalúan con el método TD-DFT/cam-B3LYP/6-311++G(d,p). Las energías HOMO y LUMO se calculan así como los valores de brecha de energía de los orbitales de frontera para una mejor comprensión de la transferencia de carga que podría ocurrir dentro de la molécula. El valor de hiperpolarizabilidad de primer orden del compuesto estudiado es 0,746 veces mayor que el valor de urea pero 709,6 veces mayor que para p-nitroanilina. Las funciones de Fukui mostraron que el anillo de fenilo en posición 1 y los átomos de nitrógeno son los sitios más probables para los ataques nucleofílicos y electrofílicos. El mapa MEP muestra que los sitios con potencial negativo son el átomo de nitrógeno en posición 2 y el fenilo en posición 3.