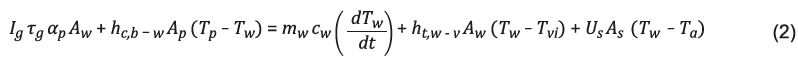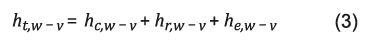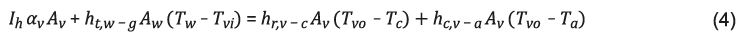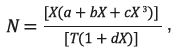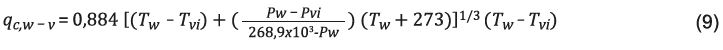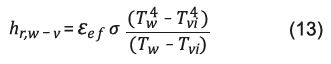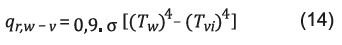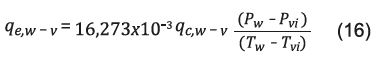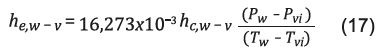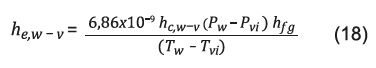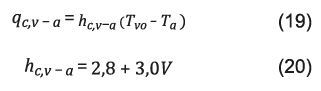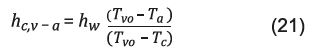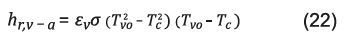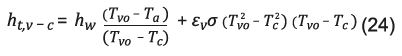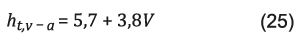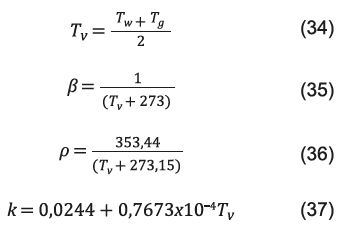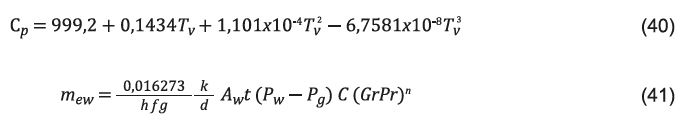Introducción
La desalinización del agua de mar se conoce desde la antigüedad 1),(2, se ha reseñado 1),(3),(4 que Tales de Mileto y Aristóteles lo mencionan en sus escritos y describen cómo se habrían utilizado dispositivos primitivos basados en hervir el agua en vasijas de barro o calderos y recogerla en esponjas en los barcos para conseguir agua dulce durante viajes largos. Desde entonces se han estudiado y desarrollado varios métodos y sistemas de desalinización que han pasado de los prototipos a instalaciones de gran capacidad y esto ha permitido conocer costos y eficiencias de las etapas en cada proceso 5),(6),(7), (8),(9.
Entre los sistemas de desalinización empleados actualmente, se estudia con mucho interés aquellos basados en energías renovables por sobre aquellos que emplean energía de combustibles fósiles 10), (11), (12), (13), (14), (15), (16. La desalinización solar o SD consiste en colocar agua de mar en un recipiente donde a través de una película transparente, generalmente vidrio, se emplea la radiación solar para calentar la solución salina y evaporar una parte del agua que pasa al aire de la cámara y posteriormente condensa al entrar en contacto con una superficie más fría desde donde se colecta 17),(18. Estos equipos no emplean otra fuente de energía y por lo tanto su rendimiento está en función de la radiación solar que se pueda captar, y de la eficiencia de los procesos al interior del equipo.
Por la forma de operación de los desalinizadores solares pasivos, todas las etapas de transferencia de masa y energía tienen límites, los cuales se analizan en este trabajo y se comparan con datos reportados, con el fin de determinar la productividad máxima teórica esperada.
Marco teórico
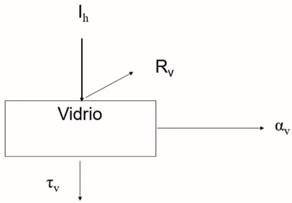
Los desalinizadores solares pasivos reciben toda la energía para su operación a partir de la radiación solar incidente, ésta se transfiere desde la cubierta de vidrio hacia el fondo del destilador y desde ahí, transformada en energía térmica, hacia el agua, las paredes, el fondo y la cubierta del equipo. Una parte de esa energía evapora agua y la restante se pierde al ambiente. Para su análisis se emplean varios modelos de transferencia de calor y masa 19),(20, así como correlaciones para las propiedades termodinámicas y de transporte del agua y del vapor 21. Los modelos matemáticos se usan para analizar el comportamiento del desalinizador en las mejores condiciones de operación para la temperatura del agua, del vidrio y la radiación solar y se comparan los resultados. Para el desarrollo del presente trabajo se considera un destilador solar pasivo de una sola cubierta representado mediante el esquema de la Figura 1.
En el destilador, se considera que no hay pérdidas de masa por fugas del equipo, que no hay gradientes de temperatura en el vidrio, el agua o el material aislante y que las variaciones debidas a la temperatura en la capacidad calorífica de la base del destilador del vidrio y del aislante son despreciables 21), (22.
Radiación solar
La radiación solar que alcanza la superficie de la tierra no es monocromática 23, abarca una gama de longitudes de onda que van del infrarrojo hasta el ultravioleta, pasando por el espectro visible. En los desalinizadores solares esta radiación Ih llega hasta la superficie del vidrio donde una fracción αb es absorbida, una fracción τv es transmitida y una fracción Rv es reflejada. La fracción transmitida atraviesa el aire húmedo con pérdidas despreciables y alcanza el agua en el fondo del destilador, donde nuevamente la radiación total se divide entre lo absorbido αw, reflejado Rw y transmitido τw. Un esquema de este proceso para el vidrio se muestra en la Figura 2, la fracción transmitida tiene el mismo compartimiento en el aire, aunque con pérdidas despreciables, al igual que en el agua del fondo del destilador.
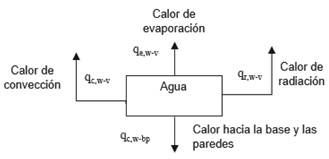
La fracción transmitida por el agua, llega hasta el fondo del destilador, generalmente pintado de color negro, donde la mayor parte se absorbe, una pequeña fracción se refleja y prácticamente nada se transmite; allí calienta la superficie del fondo del destilador, y este calor empieza a transmitirse hacia el agua y hacia el material aislante en el fondo y en las paredes del destilador. El agua es calentada y del total de la energía térmica generada que se transfiere al vidrio, una parte lo hace por convección natural, otra parte por radiación y otra parte evapora el agua de la solución salina y se transfiere en forma de calor de evaporación; esta es la única fracción de todo calor involucrado en el proceso que sirve para obtener destilado, se transfiere al vidrio donde se condensa el vapor por la diferencia de temperatura, y de allí se disipa al ambiente 24. Este proceso se muestra en la Figura 3.
La radiación solar varía de un lugar a otro dependiendo de factores como la ubicación geográfica, la época del año, la nubosidad y la hora del día. Los valores se pueden obtener por medición directa o a través de publicaciones de instituciones como el Banco Mundial. Es posible encontrar datos útiles para la mayoría de regiones 25.
En el proceso de absorción de la radiación solar, Cooper 18 y otros autores 26 han determinado que solamente entre el 85 y el 95% de la radiación Ih incidente alcanza el fondo del destilador.
Balance de energía
De acuerdo con el diagrama de la Figura 1 se plantean los balances de energía así 22:
Para el recipiente que contiene el agua en el fondo del destilador:
Donde:
I h = radiación incidente en el vidrio (W/m2),
τ v = transmisividad del vidrio, adimensional
τ w = transmisividad del agua, adimensional
α b = absortividad del recipiente o fondo del destilador, adimensional
A b = área de la base del destilador (m2),
A f = área del fondo del destilador (m2),
h c,b-w = coeficiente de transferencia de calor por convección del fondo del destilador al agua (W/ m2°C),
Tp = temperatura de la base del destilador (°C),
Tf = temperatura del fondo del destilador (°C),
Tw = temperatura del agua (°C),
Uf = coeficiente total de transferencia de calor del fondo del destilador al ambiente (W/m2°C), y
Ta = temperatura ambiente (°C).
Balance de Energía para el agua en el recipiente del destilador:
Donde:
A = área del agua del destilador (m)
m w = masa del agua en el destilador (kg),
c w = capacidad calorífica del agua (J/kg°C), dT w /dt = variación de la temperatura del agua respecto del tiempo (°C/s),
h t,w-v = coeficiente total de transferencia de calor desde el agua al vidrio (W/m2°C), y
T vi = temperatura de la cara interna del vidrio (°C).
El coeficiente total de transferencia de calor del agua al vidrio, definido por Sampathkumar 27 es
Donde:
h c,w-v = coeficiente de transferencia de calor por convección del agua al vidrio (W/m2°C),
h r,w-v = coeficiente de transferencia de calor por radiación del agua al vidrio (W/m2°C),
h e,w-v = coeficiente de transferencia de calor por evaporación del agua al vidrio (W/m2°C).
Balance de Energía para el vidrio de la cubierta
Donde:
α v = absorbancia del vidrio, adimensional A v = área del vidrio (m2), h r,v-c = coeficiente de transferencia de calor por radiación del vidrio al cielo (W/m2°C),
T vo = temperatura de la cara externa del vidrio (°C), T c = temperatura del cielo (°C), h c,v-a = coeficiente de transferencia de calor por convección del vidrio al ambiente (W/m2°C).
Correlaciones para las propiedades del agua y del aire
Para evaluar los coeficientes es necesario conocer las propiedades del agua y el aire en las condiciones de operación. Estas propiedades como densidad, viscosidad y presión de saturación de vapor, varían en función de la temperatura, por lo que se emplean correlaciones para su cálculo.
Presión de saturación o vapor del agua. Existen varias ecuaciones que relacionan la presión de vapor del agua con la temperatura, de las cuales se evalúan tres. La correlación de Dunkle 28, válida para temperaturas inferiores a 70°C, permite calcular la presión de vapor P del agua en Pa a la temperatura T (en °C) y se expresa en la Ecuación 5.
La ecuación de Antoine 29 también correlaciona presiones de vapor con temperatura para substancias en un intervalo mayor. En el caso del agua, la ecuación que es válida entre 0 y 200°C es:
Sharma y Mullic (21) presentan una ecuación de Keenan y Keyes (1936) para calcular la presión de vapor del agua, la cual es válida entre 10 y 150°C, mediante:
Donde:
X = 647,27 - T,
T = temperatura (°C),
a = 3,2437814,
b = 5,86826x10-3, c = 1,1702379x10-8, y
d = 2,1878462 x10-3.
Transferencia de calor interna
Comprende la energía transferida desde la superficie del agua hacia la superficie interna del vidrio que ocurre principalmente por radiación, convección y evaporación 27.
Calor transferido por convección. Se define el calor de convección q c,w-v en W/m2 transferido desde la superficie del agua hacia el vidrio (30) por la Ecuación 8.
Cooper 18, Sharma y Mullick 21 y Sampathkumar 27 establecen el flujo de calor desde la superficie del agua hacia el vidrio usando las ecuaciones de Dunkle:
Según Sampathkumar 27, el coeficiente de transferencia de calor de convección se puede expresar por:
Donde
P w = presión de vapor del agua a la temperatura
T w , (Pa), y
P vi = presión de vapor del agua a la temperatura de la pared interna del vidrio, (Pa).
Estas correlaciones son válidas para temperaturas de operación alrededor de 50°C y un valor de ΔT’ alrededor de 17°C, además son independientes del volumen de la cámara y válidas solamente para el flujo de calor hacia arriba en el espacio cerrado entre las superficies de evaporación y condensación.
Calor transferido por radiación. La Ecuación 12 define el calor transferido por radiación entre la superficie del agua y la superficie interna del vidrio 30:
Donde:
q r,w-v = calor transferido por radiación, (W/m2),
El coeficiente de transferencia de calor por radiación se define en la Ecuación 13 empleando la constante de Stefan-Woltzman σ:
Donde:
ԑef = emisividad efectiva, adimensional, y σ = 5,67x10-8 (W/m2K4).
Cooper 18 y Sharma-Mullick 21 establecen como un valor estimado de 0,9; reemplazándolo en la ecuación 13 y ésta en la 12 se obtiene:
Para obtener datos más exactos o casos particulares, la emisividad efectiva se calcula a partir de las emisividades del vidrio ԑ v y del agua ԑ w , mediante la Ecuación 15 (27).
Calor transferido por evaporación. El calor q e,w-v en W/m2 transferido por evaporación desde el agua hacia el vidrio, como función del calor de convección, según Cooper 18 es:
Los valores de los coeficientes están relacionados de acuerdo con Setoodeh (31) mediante la Ecuación 17, donde se asume que el calor de vaporización del agua es constante.
El coeficiente de transferencia de calor por evaporación según Sharma y Mullick (21) es definido por la Ecuación 18. Esta ecuación incluye las variaciones del calor de vaporización del agua con la temperatura.
Coeficiente total de transferencia entre el agua y el vidrio. De acuerdo con el balance expresado en la Ecuación 2, el coeficiente total de transferencia se puede calcular por la Ecuación 3 27.
Transferencia de calor externa. El calor se pierde en el destilador solar desde la superficie del vidrio hacia el ambiente por convección natural y radiación, y por las paredes y el fondo del destilador solar, que tienen un material aislante, por radiación y convección (27). Se analizará únicamente el calor perdido por el vidrio al ambiente por convección natural, y por radiación; asumiendo que en comparación con aquellos, el calor perdido por las paredes y el fondo es despreciable.
Calor transferido por convección. Las pérdidas de calor por convección q c,v-a en W/m2 del destilador se pueden expresar en función de la velocidad del viento. Aboul-Einein 22, Shukla 32) y Sampathkumar 27 emplean para el calor perdido y el coeficiente de transferencia entre el vidrio y el ambiente una correlación propuesta por Duffie and Beckman (1980):
Donde:
V = velocidad del viento (m/s).
El coeficiente de transferencia de calor por convección perdido por el destilador solar desde el vidrio hacia la atmósfera, o hacia el cielo, según Sharma y Mullic 21 se define en la Ecuación 21:
Donde
h c,v-c = coeficiente de transferencia de calor por convección (W/m2), y
h w = coeficiente de transferencia de calor debido al viento (W/m2).
Coeficiente de transferencia de calor por radiación entre el vidrio y el ambiente. El coeficiente de transferencia de calor de radiación transferido entre el vidrio y el ambiente definido por Mullick 21 es:
Donde:
ε g = emisividad del vidrio, adimensional T c = temperatura del cielo, (K).
Coeficiente de pérdidas totales de calor entre el vidrio y el ambiente. Este coeficiente comprende la suma de las pérdidas por convección y por radiación, y se expresa mediante la Ecuación 23:
Donde:
h t,g s = coeficiente total de transferencia de calor entre el vidrio y el ambiente, (W/m2K), Reemplazando las definiciones de la ecuación 21 y 22 en la ecuación 23 se obtiene:
Algunos autores (1, 27, 33) emplean para el cálculo del coeficiente de pérdidas totales desde el vidrio al ambiente en función de la velocidad del viento una correlación que se muestra en la Ecuación 25.
Indicadores de rendimiento
Productividad empleando el calor de evaporación. La tasa de evaporación de agua instantánea mew en kg/s, de acuerdo con Mowla 34, está dada por:
La evaporación M ew para un período de tiempo t es:
Si el período de tiempo es una hora, en segundos, se tiene 20), (22), (32:
Para Setoodeh 31 y Sampathkumar 27 la masa de agua evaporada m ew en un período de tiempo t se puede calcular por la Ecuación 29.
Sampathkumar 27 define la producción diaria, incluyendo las horas de la noche, como:
Productividad empleando los números adimensionales Pr y Gr. Este método 19),(27, emplea los números adimensionales de Prandtl y Grashoff, como se muestra en la Ecuación 31.
Donde: k = conductividad térmica del aire húmedo
(W/ m°C), y
d = longitud media característica entre las superficies de evaporación y de condensación (m), C = constante, adimensional Gr = número de Grashoff, adimensional y Pr = número de Prandtl, adimensional.
Los números adimensionales de Grashoff y Prandtl son:
Donde:
β = factor del coeficiente volumétrico de expansión
térmica del aire (K-1), ρ = densidad del vapor (kg/m3), y μ = viscosidad del aire húmedo (Pa.s).
Setoodeh 31 también presenta una correlación para ciertas propiedades que se evalúan a T v que es la temperatura promedio entre T w y T g :
Donde para T < 70°C el calor latente de vaporización del agua h f g es:
Para la viscosidad:
La capacidad calorífica del aire:
Reemplazando las definiciones y despejando , se establece 19 que la productividad m ew se puede calcular empleando los números de Grashoff y Pandtl mediante la Ecuación 41:
Los valores de C y n se calculan, como propone de cada destilador solar y del intervalo de temperatura Tiwari 33, mediante regresiones a partir de datos del agua en que operan, por lo que se deben experimentales; en su trabajo, Sampathkumar 27 determinar en cada caso particular. En la Tabla 1 se establece que C y n dependen del diseño específico presentan algunos valores reportados para C y n.
Productividad empleando la radiación solar incidente. P. I. Cooper 18 en su trabajo presenta una correlación lineal, válida para niveles de radiación Ih entre 0,4 y 1,39 kW/m2 y para una temperatura ambiente de 30°C, para calcular la productividad instantánea la cual se muestra en la Ecuación 42.
Eficiencia
A partir del agua evaporada. Para calcular la eficiencia η t de un destilador solar pasivo a partir del calor de vaporización la masa de agua condensada y la radiación incidente medida, se emplea la Ecuación 43 20:
Donde:
A s = superficie de la base del destilador, (m), y ∆t = período de tiempo, (s).
Eficiencia máxima teórica a partir de la radiación solar. Cooper 18 presenta una ecuación para hallar la eficiencia máxima teórica diaria que se muestra en la Ecuación 45. Empleando esta ecuación se obtienen datos más altos que los hallados empleando la ecuación 44 para el mismo caso.
Donde:
η o = eficiencia máxima teórica diaria, adimensional, θ s = horas de luz de un día medidas desde la salida del sol hasta el ocaso, (h).
Para los cálculos se consideran los datos 35 de un destilador solar con los valores presentados en la Tabla 2 22:
Donde xa y xv son el espesor del agua y del vidrio respectivamente y kv la conductividad térmica del vidrio.
Resultados
Desviaciones de las correlaciones para estimar la presión de saturación de vapor del agua. La presión de vapor del agua entre 0 y 100°C calculada mediante las correlaciones de Antoine, Sharma y Dunkle difieren entre sí y con respecto a los datos de Lemmon, McLinden y Friend reportados en Perry 36; su desviación se muestra en la Figura 4.
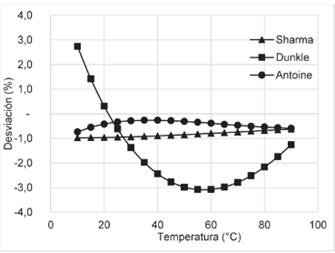
Figura 4 Desviación porcentual de la presión de vapor del agua calculada según las correlaciones de Dunkle, Antoine y Sharma-Mullick (Keenan-Keyes).
Se aprecia que la correlación de Dunkle es la que presenta mayores desviaciones, entre +2,7 y -3,1%, mientras que los menores valores son para la de Antoine con -0,4 y 0,7%.
Transferencia de calor interna
Calor de convección
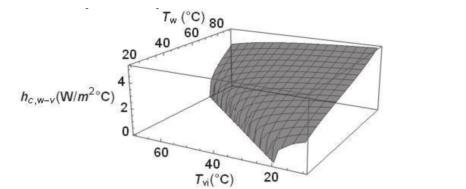
En la Figura 5 se muestra el comportamiento del coeficiente de transferencia de calor por convección en función de la temperatura del agua Tw y la temperatura de la cara interna del vidrio Tvi. Se aprecia que se incrementa a medida que aumenta Tw y disminuye Tvi.
Calor transferido por radiación
El comportamiento del coeficiente de transferencia de calor por radiación con respecto a las temperaturas del agua T w y del vidrio T se aprecia en la Figura 6. El coeficiente puede alcanzar 9,0 W/m 2 v °C cuando la diferencia de temperatura es de 50°C, valores superiores, cuando ambas temperaturas son iguales o la temperatura del vidrio es mayor que la del agua, carecen de sentido físico. La magnitud del coeficiente aumenta a medida que se incrementa la temperatura del agua y disminuye la temperatura del vidrio.
Calor de evaporación
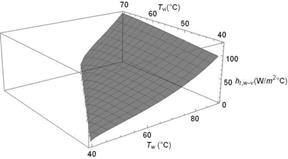
El comportamiento del coeficiente de transferencia de calor de evaporación calculado a partir de la ecuación 17 en función de las temperaturas del agua y del vidrio se muestra en la Figura 7. El valor que alcanza este coeficiente es mucho mayor en magnitud que el calor de convección y el calor de radiación, alrededor de 120 W/m2°C para diferencias de temperatura de 60°C, el segmento donde la temperatura del vidrio es mayor que la del agua, carece de sentido físico.
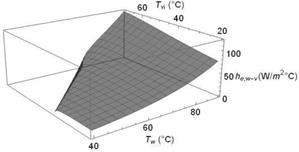
Figura 7 Coeficiente de transporte de calor por evaporación propuesto por Mowla y Tiwari h e,w-v en función de las temperaturas del agua T w y la cara interna del vidrio T vi .
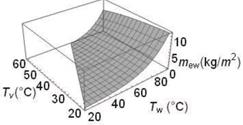
Los valores calculados con las Ecuaciones 17 y 18 varían muy poco. El comportamiento del coeficiente de transferencia de calor por evaporación entre el agua y la superficie interna del vidrio calculado mediante la Ecuación 18 se muestra en la Figura 8.
Coeficiente total de transferencia entre el agua y el vidrio
Corresponde a la suma del calor transferido por radiación, convección y evaporación, se calcula con la ecuación 3 y se muestra en la Figura 9. Este coeficiente puede alcanzar hasta 135 W/m2°C para diferencias de temperatura de 50 °C.
Indicadores de rendimiento
Productividad empleando el calor de evaporación
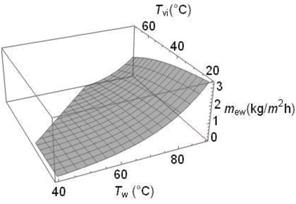
El comportamiento de la productividad diaria calculada a partir de los coeficientes de transferencia por convección y por evaporación, por la Ecuación 30, se observa en la Figura 10 en función de T w y T vi.
Productividad empleando números adimensionales
En la Figura 11 se observa el comportamiento de la productividad en función de las temperaturas del agua y del vidrio, donde se han empleado 0,0112 y 0,4088 para C y n respectivamente. Se debe notar que en este caso, los valores de productividad son menores que aquellos mostrados en la Figura 10 en las mismas condiciones de temperatura calculadas empleando el calor de evaporación. Los valores máximos reportados en la práctica alcanzados para la productividad son alrededor de 0,550 kg/m2h 33. Se aprecia que la productividad aumenta con el incremento de la temperatura del agua y la disminución de la temperatura del vidrio.
Magnitudes de los coeficientes de transferencia
Empleando los modelos de transferencia descritos, se puede calcular un rango que pueden alcanzar los valores de los coeficientes de transferencia de calor, que se muestra en la Tabla 3.
Tabla 3 Valores que alcanzan los coeficientes de transferencia de calor en los destiladores solares pasivos
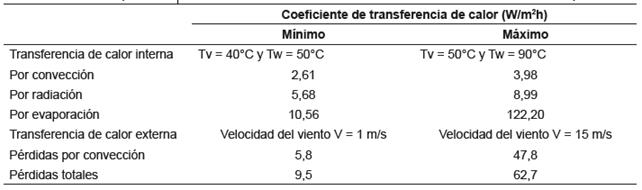
En la tabla 3 se aprecia que en condiciones de bajas temperaturas y con una baja velocidad del viento, el total de energía incidente solamente se puede aprovechar en un 37 % sin considerar las pérdidas por reflexión del material transparente que varían entre 10 y 15 % de la radiación incidente 18, y en condiciones de alta temperatura y alta velocidad de viento este calor evaporativo puede alcanzar hasta un 62 % del total. Esto es en condiciones ideales, considerando por ejemplo que todo el tiempo el cristal del evaporador está en posición perpendicular respecto a la radiación incidente, lo cual no se cumple en los evaporadores solares pasivos. La velocidad del viento afecta de dos maneras el proceso; enfriando la cara externa del vidrio del evaporador y ayudando en la condensación, y al mismo tiempo enfriando el resto del equipo, por lo que una alta velocidad incrementa las pérdidas por convección.
Productividades teóricas y experimentales
Se ha calculado la productividad máxima teórica a partir de la radiación solar mediante la ecuación 44 y se muestra junto con los datos obtenidos experimentalmente en varios ensayos en la Figura 12.
Las máximas productividades teóricas se ubican entre 0,42 y 0,75 kg/h mientras que las experimentales alcanzan máximos entre 0,15 y 0,30 kg/h. De acuerdo con el atlas publicado por el Banco Mundial 25, hay zonas de alta radiación solar que alcanzan un promedio anual entre 7,2 y 7,4 kW.h/m2, empleando este modelo 18, el valor de productividad de 6,7 a 6,9 kg/m2día representa un máximo teórico en condiciones ideales.
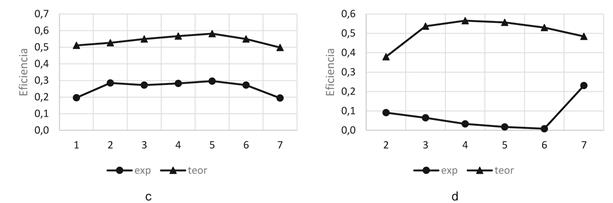
Se ha calculado la eficiencia máxima teórica empleando la Ecuación 43 del modelo de radiación solar y se presenta en la Figura 13 junto con la eficiencia obtenida experimentalmente en varios ensayos.
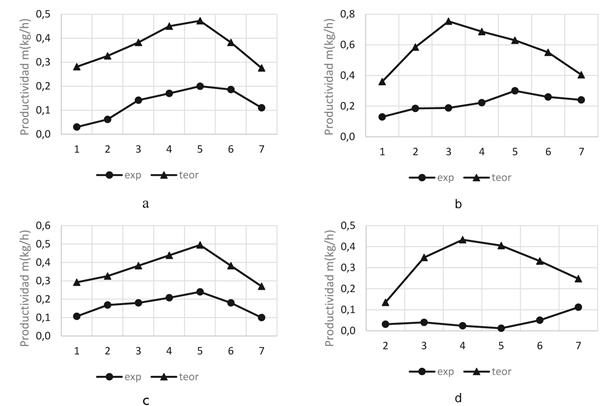
Figura 12 Comparación de productividades máxima teórica y experimental para cuatro casos. a) Shukla 32),(32, c) 32 y d) Dev 37.
Conclusiones
En un destilador solar pasivo siempre estarán presentes los mecanismos de transferencia por convección y radiación al interior, así como las pérdidas por reflexión y convección al exterior, por lo tanto el calor aprovechable máximo teórico para evaporar el agua oscilará entre 33 y 56 % de la radiación solar total en condiciones ideales.
El rendimiento del destilador solar calculado mediante el modelo de los coeficientes de transferencia de calor, y el calculado empleando las correlaciones de los números adimensionales proporcionan datos que representan con precisión el fenómeno, mientras que las correlaciones basadas en la radiación solar presentan los máximos teóricos para productividad y eficiencia, que son coherentemente superiores a los medidos en todos los casos.
La productividad de los destiladores solares pasivos en función de la irradiación solar disponible, tiene límites termodinámicos definidos para su productividad entre 6,7 y 6,9 kg/m2día, los cuales están determinados por la intensidad de la radiación solar incidente, los materiales de construcción, las condiciones locales de temperatura y la velocidad del viento.