Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Ingeniería e Investigación
Print version ISSN 0120-5609
Ing. Investig. vol.30 no.3 Bogotá Sept./Dec. 2010
Andrés Pantoja1 , Eduardo Mojica Nava2 y Nicanor Quijano3
1 Electronic Engineering, Universidad Nacional de Colombia Sede Manizales. M.Sc., in Electronic Engineering, Universidad de los Andes. Ph. D., Student, Universidad de los Andes. Universidad de Nariño, Pasto. ad.pantoja24@uniandes.edu.co
2Electronic Engineering, Universidad Industrial de Santander. M.Sc., in Electronic Engineering, Universidad de los Andes. Ph.D., in Engineering, Universidad de los Andes y Ecole Centrale Nantes, Francia. Universidad Católica, Bogotá, Colombia. ea.mojica70@uniandes.edu.co
3Electrical Engineer, Pontificia Universidad Javeriana, Bogotá, Colombia. M.Sc.,and Ph.D., in Electronic Engineering, Ohio State University, Columbus, OH,USA. Universidad de los Andes, Bogotá, Colombia. nquijano@uniandes.edu.co
ABSTRACT
The sum of squares (SOS) decomposition technique allows numerical methods such as semidefinite programming to be used for proving the positivity of multivariable polynomial functions. It is well known that it is not an easy task to find Lyapunov functions for stability analysis of nonlinear systems. An algorithmic tool is used in this work for solving this problem. This approach is presented as SOS programming and solutions were obtained with a Matlab toolbox. Simple examples of SOS concepts, stability analysis for nonlinear polynomial and rational systems with uncertainties in parameters are presented to show the use of this tool. Besides these approaches, an alternative stability analysis for switched systems using a polynomial approach is also presented.
Keywords: sum of squares (SOS), stability analysis, nonlinear systems, switched systems.
Received: april 30th 2009
Accepted: november 15th 2010
Introduction
The theory of sum of squares (SOS) decomposition of polynomial functions has achieved significant progress during the last ten years since its introduction (Parrilo, 2000). This development has resulted from possible relaxations of NP-hard problems (e.g., non-negativity proofs of multivariable polynomials) (Papadimitriou, 1994) for solvable problems in computational polynomial time. The basic problem consists of finding conditions to verify. The possible classes of F functions must be limited to study this problem from an algorithmic approach and, at the same time, to keep the problem general enough to guarantee the applicability of the results. A tradeoff is achieved when the class of F functions is restricted to polynomial functions (Parrilo, 2000)
F(x1,...,xn)≥0, ∀x1,...,xn∈Rn (1)Definition 1.1. A polynomial function f in x1, . . . , xn, with coefficients in a field k, is a finite lineal combination of monomials:
f= ∑αcαxα=∑αcαx1α1...xnαn cα>k (2)
where the sum is given over a finite number of n -− tuples
α = (α1, ..., αn), con αi∈ N0.
It is possible to show that proving polynomial function global positivit is in fact an NP-hard problem too (when the degree of the function is at least four). Therefore, a method guaranteeing the solution of this problem for any polynomial function could have unacceptable computational performance for a function having a high number of variables. This is the main disadvantage of theoretical methods so that the quantifiers are eliminated (Parrilo, 2000).
A question arises when inherent computational complexity problems must be avoided. Do some conditions guarantee the positivity of a multivariable function so that the method can be executed in polynomial time? The next section shows that SOS descomposition techniques fulfil complexity reduction conditions.
Some SOS technique applications are global, boolean and constrained optimization problems (Prajna et al., 2004). Moreover, some general control problems, such as Lyapunov's function construction for stability analysis of nonlinear systems (Topcu et al.,2008) and parameter uncertainty limitation in dynamic system analysis (Topcu and Packard, 2009) have been solved using the SOS approach. Other specific control applications are stability analysis of nonlinear systems with time delay (Papachristodoulou, 2004) and the synthesis and design of nonlinear controllers (Franze et al., 2009; Ebenbauer and Allg¨ower, 2006).
SOS techniques solve a convex optimisation problem by means of semidefinite programming (SDP) (Parrilo, 2003). This method is a generalisation of linear programming (LP) where non-negativity constraints in decision variables are replaced by positive semidefinite matrix inequalities. The methods for solving SDP are given by algorithmic techniques such as linear matrix inequalities (LMI) and numerical programmes for SDP such as SeDuMi and SPDT3 (Anjos and Burer, 2007).
Solving an SOS problem implies SDP problem construction, finding the numerical solution, and interpreting the result of the SDP problem in initial variable formulation. The Matlab toolbox SOSTOOLS (Prajna et al.,) was used for defining SOS variables,functions and constraints needed for resolving the optimisation problem in a symbolic environment.
This tutorial presents and reviews the basic concepts of SOS techniques and some control applications such as Lyapunov function construction for stability analysis of nonlinear systems, parameter uncertainty analysis in systems having rational vector fields, application in stability analysis of switching systems and the use of SOSTOOLS for solving some problems and examples.
Sum of squares (SOS)
The main concepts and basic examples of SOS techniques are presented in this section. As stated, these concepts were originally introduced by P. Parrilo (Parrilo, 2000). The examples start with SOS decomposition of a multivariable polynomial function to introduce some control applications.
The Matlab toolbox SOSTOOLS is introduced as a computational method used in the numerical solution of SOS problems introduced in this tutorial.
Basic concepts
Definition 2.1. A multivariable polynomial p(x) having degree 2d in x ∈ Rn, is a sum of squares (SOS) if there exists M polynomials fi(x) so that
p(x)= ∑i=1M f12(x) (3)
SOS decomposition can be expressed as shown by Parrilo (2003) if there is a positive semidefinite matrix Q ∈ Rn×n, so that
p(x)=Z(x)T QZ(x) (4)
where Z(x) is a vector of monomials in x with a degree less than or equal to d. Given that Q = Q,T _ 0 can be written as Q = HHT, where H ∈ Rn×r with r = rank(Q), and if h1, h2, . . . , hr, are the columns of H, then equation (4) can be expressed as
p(x)= ∑i=1 (hT1Z(x))2 (5)
Therefore, SOS decomposition can be relaxed to find matrix Q _ 0 and the resulting problem becomes a semidefinite programming issue as defined by Parrilo (2000).
The next example presents the representation of a polynomial function in an SOS form expressed as in equations (4) and (5).
Example 2.1. Find SOS decomposition of the polynomial function given by
p(x) = 13x41+14x31x2-18x21+14x21x22...
...6x1x2+9x42-30x32x1+9With a vector
Z(x) = [1 x22 x1x2 x12]T
a matrix QT≥ 0 is found so that
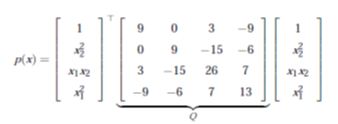
Then, with factorisation Q =HHT given by
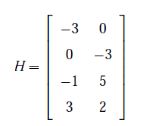
The resulting SOS decomposition is
p(x)= (3x12-x1x2-3)2 + (2x21-3x22+5x1x2)2
Clearly an SOS function is globally positive, but not all positive functions are SOS.
An example of these functions would be the Motzkin polynomial M(x) = x41 x22+x21x42+x63−3x21x22x23. To prove positivity in this class of functions using SOS techniques, Reznick (2000) has shown that if p(x) > 0, for all x ∈ Rn, then there exists a positive integer r so that
p(x)(∑ni=1x21)r is SOS
The non-negativity problem is relaxed for testing different values of r until SOS representation is possible.
SOSTOOLS computational tool
SOSTOOLS (Prajna et al.,) is a Matlab toolbox which is used to solve SOS problems with an algorithm for semidefinite programming(e.g., SeDuMi or SDPT3).This tool turns the SOS problem into an SDP problem, uses the solving algorithm and expresses the solution in the initial variables and polynomials. The general procedure for obtaining SOS problem solution using SOSTOOLS is summaryzed as follows:
- Define SOS variables, polynomials and constants using the symbolic toolbox, or in Matlab polynomial format;
- Define the problem's constraints as SOS inequalities; and
- Use the SOSTOOLS functions for solving the problem and for expressing the solution in the problem's initial variables.
The next section presents some control applications which use SOS techniques to obtain a Lyapunov function which can be used for the stability analysis of the equilibrium point for nonlinear and switched systems
Control applications
Finding a Lyapunov function to prove the stability of an equilibrium point in a nonlinear system is a difficult task, except for systems having few variables and special vector fields (e.g., energy functions and gradient systems), where specific methods (e.g., Krasovskii) could be used (Khalil, 2002).
For more general systems, SOS techniques facilitate finding an appropriate Lyapunov function using a computational tool and fixed algorithm. The conditions for verifying the stability of an equilibrium point in systems having polynomial and rational vector fields rely on non-negative functions which could result in NPHard problems. Therefore, by turning these conditions into SOS functions, the problem can be solved using the SOSTOOLS computational tool.The tool is applied to polynomial and rational systems having parameter uncertainties in the next examples using variations of the simple original algorithms and extensions of the fundamental theorems in Lyapunov analysis.
Systems having polynomial and rational vector fields
The Lyapunov stability theorem is applied to the general autonomous system given by
x.=f(x) (6)
where f : D →Rn is a continuous map from D ⊂ Rnen Rn, and without loss of generality (Khalil, 2002), the origin is an equilibrium point of (6) (i.e., f (0) = 0). If a continuously differentiable function V(x) (so-called Lyapunov function) is found, the system's stability conditions are defined by: i) if V(x) is positive definite, and ii) V(x) is negative semidefinite, the origin of (6) is stable; and ii) if V(x) is negative definite, the origin is asymptotically stable.
This theorem's conditions must be relaxed to apply the SOS techniques for proving stability in nonlinear systems to express non-negativity as SOS. In polynomial systems having state variables x = [x1, x2, . . . , xn], a function V(x) with degree 2d is defined using an auxiliary function φ(x) given by
φ(x)= ∑i=1n ∑nj=1εijx12j (7)
where e ε ≥ 0, for all i and j, and ∑aj=1εij> 0, for alli = 1,2, . . . ,n. With these conditions, j(x) is positive definite. Therefore, if V(x)−φ(x) can be expressed as SOS, it is guaranteed that V(x) is positive definite too. Stability conditions can then be expressed as:
V(x)−φ(x) es SOS (8)
- δV/δx f(x) es SOS (9)
Hence, the SOS algorithm for finding a Lyapunov function using SOSTOOLS is stated as follows:
- Define a general polynomial function V(x) with degree 2d and monomials in x with degree d;
- Create the auxiliary function φ(x) as defined in (7);
- Define the expression V(x)−φ(x) as SOS. Inequality;
- Define - δV/δx f (x) as SOS inequality; and
- Solve the SOSTOOLS programme and obtain the resulting V(x).
Example 3.1. (Khalil, 2002). Find a Lyapunov function to show asymptotical stability of the origin in the system:
x.1= x2(1-x21)
x.2= -(x1+x2)(1-x21) (10)The system has an equilibrium point in x = 0. This equilibrium is not the only one, given that in x1 = 1 y en x1=−1, x1=0 and x2=0. Then, finding a Lyapunov function that satisfies conditions (8) and (9) is not an easy task for analysing the origin's characterristics. Moreover, a region of attraction can be determined using the contour lines of the function V(x) so obtained.
Using SOSTOOLS, a function having 42 terms and degree 8 is found. Figure 1 shows the system's phase plane and the contour lines of V(x). It is shown that the biggest region of attraction is obtained when the contour lines approximate to x1 = −1, which is thelimit where the isoclines of the Lyapunov function are closed.

In a system having a rational vector field f (x), condition (9) is modified to apply the SOSTOOLS algorithm. In this case, a function w(x) > 0 must be found so that
-w(x)- δV/δx f(x) sea SOS and polynomial (11)
If w(x) > 0, the second condition of the general stability theorem is satisfied, and if (11) is a polynomial function, the SOS techniques can be applied as shown in the next example.
Example 3.2. (Khalil, 2002). Find a polynomial Lyapunov function to show stability of the origin of the system given by
p>x.1= -6x1/(1+x21)2 +2x2x.2= -2(x1+x2)/(1+x12)2 (12)
Choosing w(x) = (1+x21)2 ≥ 0, and given that V(x) is a polynomial function, the algorithm for finding the Lyapunov function must include −(1+x12)2 δV/δx f (x) as SOS inequality to satisfy the second condition of the stability theorem.
The result of this SOSTOOLS programme is a function V(x) with 62 terms and degree 10. The phase plane and some contour lines of V(x) (i.e., regions of attraction of the origin) are shown in Figure 2.
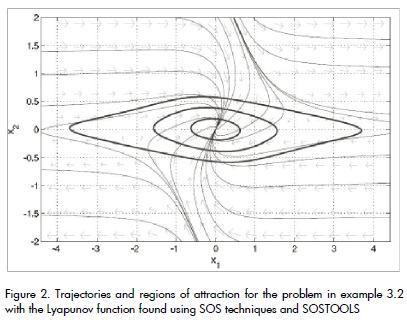
The system in (12) has a unique equilibrium point in x = 0, and the Lyapunov function obtained leads to establishing regions of attraction for the origin.
Although the Lyapunov functions found in examples 3.1 and 3.2 have a high number of terms, these functions are in the Matlab symbolic environment which facilitates plotting and verifying stability conditions.
Besides, the examples presented here have given a glimpse of the use of SOS techniques for analysing more complex and higher order systems.
Systems with parameter uncertainties
Consider the general nonlinear system given by equation (6) with parameter uncertainties expressed as
ci(x,u)≤0 para i=1,...,N1 (13)
where u ∈Rm is the set of uncertain parameters, and N1 is the number of required constraints.
Assume that functions ci can be expressed as polynomial functions in (x,u), and that f (x,u) is a rational or polynomial vector field in (x,u) without singularities in D ⊂ Rn×m, where D = {(x,u) ∈ Rn×m|ci(x,u) ≤ 0, for all i. Without loss of generality, it is assumed that f (x,u)= 0 for x = 0 and u ∈ D0 u , donde D0 u = {u ∈ Rm|(0,u) ∈ D}.The following theorem taken from Papachristodoulou and Prajna (2002) gives us the conditions for local stability of the origin of the system (6) constrained by (13).
Theorem 3.1. Suppose that for the system described above, there are polynomial functions V(x), w(x,u), and pi(x,u) so that: V(x) is positive definite in a neighbourhood of the origin, w(x,u) > 0 and pi(x,u) ≥ 0 in W Then, if
it guarantees that the origin of the state space is a stable equilibrium of the system (6). In the case where f (x,u) is a rational vector field, a function w(x,u) > 0 must be chosen so that −w(x,u)δV/δx f(x,u) is a polynomial function, and SOS algorithm can be applied without additional modifications. These conditions can be relaxed to SOS definitions according to the following proposition taken from Papachristodoulou and Prajna (2002).
Proposition 3.2. For a polynomial function φ(x) ≥ 0 (or SOS) defined as in equation (7), the local stability of the origin of (6) can be guaranteed if:
V(x)−φ(x) is SOS (i.e., V(x) is positive definite). Z(x,u) is SOS.
pi(x,u), is SOS, for i = 1, . . . , N1.
Using this proposition, the algorithm to find the Lyapunov function preserves the first three steps used in systems without constraints. The differences for systems with parameter uncertainties are defined for the condition given by (14). The next steps are required for this definition:
- Define a number of SOS functions pi(x,u) equal to the number of inequality constraints in the problem;
- Choose a function w(x,u) > 0 if necessary for a rational vector field f (x,u);
- Define −w(x,u)δV/δx f(x,u) + ∑ pi(x,u)ci(x,u) as SOS inequality; and
- Solve the SOSTOOLS problem and obtain V(x).
The next example applies the previously described procedure for evaluating the stability of the equilibrium point in a multi-zone thermal system with a controller based on evolutionary game theory (Pantoja and Quijano, 2008).
Example 3.3. A system with multiple disjoint temperature zones can be modelled by
Ti=-aiTi+bixi+aiTa
where Ti is the temperature in the ith zone (i = 1, . . . ,N), ai,bi are positive constants, Ta is ambient temperature and xi is control input for zone i. Assuming that B is a temperature limit so that B >> Ta, and with variable change qi = B−Ti the system can be expressed by:
qi.= -aiqi-bixi+ai(B-Ta) (15)
The control signal dynamics are designed so that the temperature in all zones achieves an equilibrium point equal to the maximum uniform temperature that can be obtained with a limited amount of power resources. The control strategy is given by the replicator dynamics concept (Pantoja and Quijano, 2008):
x1.= x1 (q1-1/P∑j=1Nxjqj) (16)
where P > 0 is the total available amount of resources for heating all zones. Then ∑j=1Nxi= P. The equilibrium point of the complete system composed by equations(15) and (16) is:
x*1=aj/bjP/∑j=1N aj/bj
q*1= (B-Ta)- P/∑j=1N aj/bj
The final temperature in each zone is given by:
T1*= Ta+P/∑j=1N aj/bj, para i =1, ...,N
which is clearly constant and depends on the system's parameters and on the available resources.
The proposed problem is to analyze the stability of the equilibrium point, given limited variations in the parameters of each zone ai and bi for a two-zone system (i.e., N = 2).
To express the system in "error coordinates" so that the equilibrium point is displaced to the origin, the displacement variables are eqi = qi−q*iy exi= xi−x*i. Taking into account that x1 + x2 = P, x*2 = P−x*1,, then ex2 = −ex1. With these conditions, the system is given by:
e.1= (ex1+Pa1b2/a1b2+a2b1)(eq2-eq1)...
(a1b2/a1b2+a2b1 + ex1/P -1)
e.q1=-a1eq1-b1ex1e.q2= -a2eq2+b2ex1
and the origin is the unique equilibrium point.
Appropriate estimated ranges for the parameters' variations are:
0 < ai< 2 para i = 1,2
0 < bi < 0,01 para i = 1,2
These inequalities must be expressed in polynomial form to be included in the SOS algorithm. For this purpose, if we assume that a and a are the lower and higher limits for a, respectively, inequality a < a < a is expressed as (a−a) (a−a) < 0. Defining polynomials pi(x,u), for i = 1,2 as SOS variables, and w(x,u) = (a1b2+a2b1)2 > 0, condition (14) is implemented as SOS inequality in the SOSTOOLS algorithm.
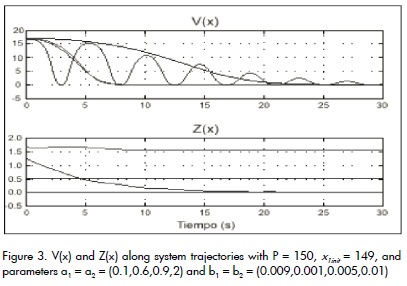
The resulting V(x) is a Lyapunov function with 32 terms and 4 degrees whose trajectories throughout the system's solutions are shown in Figure 3 for different parameter values within the specified ranges, with P = 150, and initial condition x1 = 149. Moreover, this Figure presents the trajectories of Z(x,u) for the same conditions.
It is interesting to notice that V(x) and Z(x,u) just need to be positive to satisfy the conditions in Theorem 3.1. Near the fixed limits of uncertainty, the functions are close to zero, showing the activation of the constraints and the need for finding another Lyapunov function for a wide range of uncertainties.
With the results presented in Figure 3, the equilibrium point of the controlled multi-zone temperature system is asymptotically stableas shown in Pantoja and Quijano (2008).
Switched systems
This section deals with switched systems' stability analysis (i.e. continuous systems having switching signals) using dissipation inequalities under arbitrary switching.
This method leads to finding a common Lyapunov function for switched systems.
An efficient numerical method is presented using the simple stability result for stability analysis of polynomial differential-algebraic equations (Mojica- Nava et al., 2010).
Polynomial approach for switched systems: A switched system is a system that consists of several continuous-time systems with discrete switching events. A switched system may be obtained from a hybrid system by neglecting the details of discrete behaviour and instead considering all possible switching patterns from a certain class. The mathematical model can be described by
x.(t)=fσ(t)(x,u,t) (17)
where fi : Rn×Rm×R+→Rn are vector fields, exogenous input u ∈ Rm and σ [0, tf ] → Q ∈ {0,1,2,...,q} is a piecewise constant function of time. Every mode of operation corresponds to a specific subsystem ˙ x(t) = fi(x,u, t), for some i ∈ , and the switching signals determine which subsystem is followed at each point in time, into interval of time [0, tf], with tf as final time. The control inputs, σ and u, are both measurable functions.
This general definition of switched systems leads to obtaining a polynomial expression that is able to mimic switched system behaviour which is developed using a new variable s, which works as a ontrol variable or a parameter. The starting point is to rewrite (17)
as a continuous non-switched control system in its more general case.
First, a drift vector field F(x,u) : Rn×Rm →Rn
F(x,u)=[f0(x,u)f1(x,u)...fq(x,u) (18)
is defined where fi(x,u), i ∈Q is the function for each subsystem of the switched systems given in (17). Now, to find a polynomial expression, we need for each i ∈ Q = {0,1,. . . ,q}, a quotient lk with the property that lk(i) = 0 when i ≠ k, and lk(k) = 1. Let L be the vector of Lagrange polynomial interpolation quotients (Burden and Faires, 1985) defined with the new variable s, i.e.
L(s)=[l0(s),l1(s),...,lq(s)]T (19)
Where
lk(s)= Πqi=0,l=/k(20)
On the other hand, a complementary polynomial can be used to constrain s to take only integer values. Let Q(s) be the constraint polynomial so that
Q(s)=Πqk=0 (s-k) =0 (21)
A related continuous polynomial system of the switched system(17) is constructed in the following proposition taken from Mojica- Nava et al. (2010).
Proposition 3.3. Consider a switched system of the form given in(17) with a drift vector field which are in the form given in (19). Then, there exists a unique polynomial P of order q+1 with property f. This polynomial is given by
P(x,u,s)= F(x,u)L(s)
= ∑qk=0 fk(x,u)lk(s) (22)
where s ∈ R, and lk(s) is given by (21). Now, the system (17)takes the constrained continuous form of a non-linear differential algebraic equation
x.=P(x,u,s)
0=Q(s) (23)
for each i ∈ Q = {0,1,...,q} subject to the constraint polynomial Q(s) given in (21).
Polynomial representation means that the approach presented recently for constrained polynomial control systems based on dissipation inequality can now be applied. Notice that this polynomial representation can also be used for finding a common Lyapunov function using traditional methods, but dissipation inequalities are used to provide possibilities for future work in analysing energy dissipation in switched systems, a topic which has not been widely studied (Zhao and Hill, 2008).
The next section presents the main results obtained for stability analysis of switched systems using dissipation inequalities.
Results in stability analysis using dissipation inequalities
The following theorem taken from Ebenbauer and Allgower (2004)gives a simple stability result for the general differential-algebraic systems of type (23).
Theorem 3.4. Equilibrium point x = 0 from the differential-algebraic system (23) is stable for any admissible input s = s(t), if there exists a Lyapunov function candidate V : Rn → R, a function ρ: R(μ+2)(n+q) → R, and an integer number μ so that dissipation inequality
∀ V(x)x.≤ //Gμ(ξ,ς) (24)
is satisfied for some x-neighbourhood Ωx((ξ ,ς) = 0).
The main idea behind inequality (24) is just to check negative emidefiniteness of ˙V regarding the constraint set.
It is very difficult to search for a Lyapunov function V and a function r for practical problems. However, recently established methods based on semidefinite programming and SOS decomposition allow very efficiently verifying Lyapunov inequalities of form (24)in the case where G, V, r are assumed to be polynomials(Ebenbauer and Allg¨ower, 2004). Certainly, in our case, functions G, V, and r are all polynomial. In this case, the differentiation index of the differential-algebraic system is known, therefore it is reasonable to choose m to be equal to the differentiation index (i.e., µ = 1) (Mojica-Nava et al., 2010). Therefore, µ = 1 may be chosen and if we try to prove global stability of the system (22), the following polynomial inequalities must be satisfied,
V(x) > 0
∀ V (x) P(x,s) ≤ //Q(s)//2ρ(x,s)
which implies that
for all x = (x, ˙ x, s) ∈ R2n. Note that if V is polynomial and positive definite, it implies that V is radially unbounded.
For illustration and clarity of exposition, consider the case when q = 1. Dissipation inequality is
∀ V (x)(f0(x)(1-s)+f1(x)s≤//s(1-s)//2ρ(x,s) (26)
Using SOS concepts, inequality (26) can be posed as follows. Find polynomial V(x) so that
V(x)-φ(x)≥0 es SOS
-∀ V (x)(∑qk=0fk(x,u)lk(s))+...
//Πqk=0 (s-k)//2ρ(x,s)≥0 es SOS (27)
polynomials V(x), r (x, s) and positive definite function j(x) can be computed using SOSTOOLS (Prajna et al.,).
Numerical example: switched system: Consider the switched system described by ˙ x = fi(x), x = [x1 x2]T , with
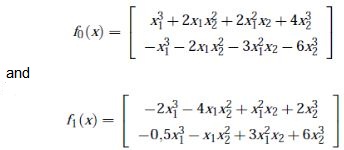
This system is considered to be a homogeneous switched system presented in stability analysis (Zhang et al., 2007). Polynomial equivalent representation is used to prove stability under arbitrary switching:
x.(t)=f0(1-s)+f1s
s∈Γ ={s∈R/Q(s)=s(s-1)=0
Using these polynomial matrices and equation (27), the following is obtained:
-δV/δxf0(1-s)+f1(s)+(s4-2s3+s2)λ(x,s)≥0
Using SOSTOOLS, a Lyapunov function of degree six is found, i.e.
V(x)= -0,0364x21+0,02x41-0,0082x42+0,0476x22...
-0,056x1x2+0,0113x21x22-0,064x1x32-0,0457x61
...-0,016x41x42+0,0034x62
which, through theorem 3.4, proves that the homogeneous nonlinear switched system reformulated as a polynomial DAE is stable.
Conclusions
This tutorial has presented SOS techniques as effective criteria for proving the non-negativity of multivariable polynomial functions. Although determining non-negativity of a function could be an NPhard problem, using SOS decomposition is an efficient method for solving this problem. Moreover, by means of the SOSTOOLS computational tool the problem can be simplified to (appropriately) use the SOS algorithm, taking into account the inherent numerical errors and high computational cost of this tool for relatively high order systems. Some SOS conditions are given for analysing rational systems with nonlinear controllers and switched systems using a polynomial approach based on stability analysis of nonlinear polynomial systems. The SOS techniques were used to consider the parameters' variations and possible uncertainties as inequality constraints on the original systems. Moreover, from the methods used to solve the presented examples it can be seen that SOS techniques are a useful method for dealing with high order and complex systems.
Anjos, M., Burer, S., On handling free variables in interior-point methods for conic linear optimization., SIAM Journal on Optimization, 18(4), 2007, pp.1310-1325. [ Links ]
Burden, R., Faires, J. D., Numerical Analysis PWS, Boston, 1985. [ Links ]
Ebenbauer, C., Allgöwer, F., Computer-Aided Stability Analysis of Differential-Algebraic Equations., In Proceedings of the NOLCOS, 2004, pp. 1025-1030. [ Links ]
Ebenbauer, C., Allgöwer, F., Analysis and Design of Polynomial Control Systems Using Dissipation Inequalities and Sum of Squares., Computers & Chemical Engineering, 30 (10-12), 2006, pp. 1590- 1602. [ Links ]
Franze, G., Casavola, A., Famularo, D., Garone, E., An off-line MPC Strategy for Nonlinear Systems Based on SOS Programming., Nonlinear Model Predictive Control, LNCIS 384, 2009, pp. 491-499. [ Links ]
Khalil, H., Nonlinear Systems., Prentice Hall Upper Saddle River, NJ, 2002. [ Links ]
Mojica-Nava, E., Quijano, N., Rakoto- Ravalontsalama, N., Gauthier, A., A Polynomial Approach to Stability Analysis of Switched Systems., Systems and Control Letters, 59(2), 2010, pp. 98-104. [ Links ]
Pantoja, A., Quijano, N., Modeling and Analysis for a Temperature System Based on Resource Dynamics and the Ideal Free Distribution., In Proceedings of the American Control Conference, 2008, pp. 3390-3395. [ Links ]
Papachristodoulou, A., Analysis of Nonlinear Time- Delay Systems Using the Sum of Squares Decomposition., In Proceedings of the American Control Conference, 2004, pp. 4153-4158. [ Links ]
Papachristodoulou, A., Prajna, S., On the Construction of Lyapunov Functions Using the Sum of Squares Decomposition., In Proceedings of the 41st IEEE Conference on Decision and Control, 2002, pp. 3482-3487. [ Links ]
Parrilo, P., Structured Semidefinite Programs and Semialgebraic Geometry Methods in Robustness and Optimization., Ph.D. thesis, California Institute of Technology, 2000. [ Links ]
Parrilo, P., Semidefinite Programming Relaxations for Semialgebraic Problems., Mathematical Programming, 96(2), 2003, pp. 293-320. [ Links ]
Prajna, S., Papachristodoulou, A., Parrilo, P., SOSTOOLS: Sum of Squares Optimization Toolbox for MATLAB-User Guide., Control and Dynamical Systems, California Institute of Technology, Pasadena, CA, 91125. Available on http://www.cds.caltech.edu/sostools. [ Links ]
Prajna, S., Papachristodoulou, A., Seiler, P., Parrilo, P., SOSTOOLS: Control Applications and New Developments., In Proceedings of the IEEE International Symposium on Computer Aided Control Systems Design, 2004, pp. 315-320. [ Links ]
Reznick, B., Some Concrete Aspects of Hilberts 17th Problem., Contemporary Mathematics, 253, 2000, pp. 251-272. [ Links ]
Topcu, U., Packard, A., Local Stability Analysis for Uncertain Nonlinear Systems., IEEE Transactions on Automatic Control, 54(5), 2009, pp. 1042-1047. [ Links ]
Topcu, U., Packard, A., Seiler, P., Local Stability Analysis Using Simulations and Sum-of-SquaresProgramming,, Automatica, 44(10), 2008, pp. 2669- 2675. [ Links ]
Zhang, L., Liu, S., Lan, H., On Stability of Switched Homogeneous Nonlinear Systems., J. Math. Anal. Appl, 334, 2007, pp. 414-430. [ Links ]
Zhao, J., Hill, D., Passivity and Stability of Switched Systems: A Multiple Storage Function Method., Systems & Control Letters, 57, 2008, pp. 158- 164. [ Links ]











 text in
text in 


