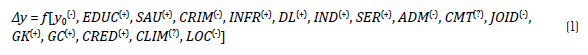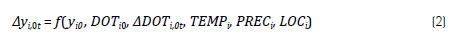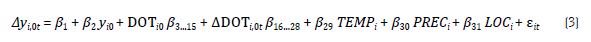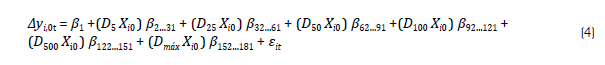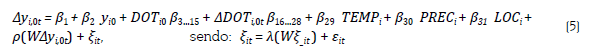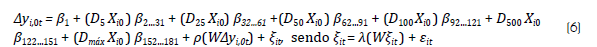1. INTRODUÇÃO
Na teoria econômica é comum encontrar estudos sobre a acumulação da atividade produtiva em certas áreas. A princípio, a produção se concentraria em locais com mais recursos naturais (condição inicial) e seria impulsionada pela atração de trabalhadores (Ottaviano e Thisse, 2004). No entanto, a consolidação desses "centros produtivos e populacionais" dependeria dos ganhos de escala (externalidades Marshallianas), da especialização (knowledge spillovers), dos encadeamentos produtivos (backward e forward-linkages) e dos menores custos de transporte decorrentes da própria aglomeração (Marshall, 1890; Prébisch, 1949; Perroux, 1950; Isard, 1956; Myrdal, 1957; Hirschman, 1958; Boudeville, 1966; Fujita, Krugman e Venables, 1999).
Embora a heterogeneidade na dotação de recursos naturais seja o ponto de partida dessas aglomerações econômico-populacionais (Starret, 1978), elas também dependeriam da ação humana (Gallo e Ertur, 2003; Ottaviano e Thisse, 2004), que poderia criar (ou não) as condições para que essas vantagens locais se destacassem (Thirlwall e Pacheco-López, 2017). Na verdade, List (1841) já havia mencionado que as vantagens absolutas e relativas de cada região poderiam ser construídas ao longo do tempo, ou seja, não seriam apenas herdadas do acaso.
O problema é que, além de originar os "grandes centros", a heterogeneidade espacial - isto é, as diferentes dotações de clima, relevo e recursos - também pode afetar os efeitos das políticas econômicas (Almeida, 2012). Além disso, Almeida e Firme (2023) demonstram que os efeitos dos fatores associados ao crescimento econômico tornam-se instáveis devido à heterogeneidade entre os municípios brasileiros. Como as disparidades locais podem tanto estimular quanto inibir estas aglomerações econômico-populacionais, é razoável supor que há maior heterogeneidade entre áreas com diferentes portes populacionais. Assim, localidades com populações semelhantes seriam mais homogêneas entre si e demandariam políticas próprias a este grupo (que, não necessariamente, funcionariam em locais cuja população é maior ou menor).
A pesar da extensa literatura sobre os condicionantes do crescimento econômico (seção 2), e dos indícios de que tanto os salários quanto o próprio crescimento variam conforme o tamanho da população local (Resende, 2014; Almeida e Firme, 2023), não foram encontrados estudos que analisem os efeitos desses condicionantes em economias com diferentes faixas populacionais. Com o objetivo de preencher essa lacuna, esta pesquisa utiliza um painel espacial com variáveis de controle e dummies interativas, contemplando dados de 5505 municípios brasileiros entre os anos 2000, 2010 e 2020, para identificar as ações mais adequadas a cada porte populacional. Os resultados indicam que cada município demandaria ações específicas para os problemas da faixa populacional à qual pertence, inviabilizando o uso de políticas universais, válidas/efetivas para localidades marcadamente heterogêneas.
O restante do trabalho está organizado da seguinte forma: a segunda seção mostra a relação entre o porte populacional e o nível de renda dos municípios brasileiros, bem como os demais fatores associados ao crescimento econômico. A terceira seção descreve a metodologia e a base de dados; Em seguida, apresentam-se os resultados, as considerações finais e as referências.
2. PORTE POPULACIONAL, NÍVEL DE RENDA E OUTROS INDUTORES DO CRESCIMENTO ECONÔMICO
Para Figueiredo (2008), o fato de não haver uma classificação oficial sobre o tamanho dos municípios brasileiros gera diferentes categorizações sobre o tema (Amorim Filho e Serra, 2001; Calvo et al, 2016; Willemann et al, 2019; Almeida e Firme, 2023). Logo, visando realçar a heterogeneidade econômica em municípios com diferentes portes populacionais, considerou-se seis possíveis faixas (Tabela 1), conforme Calvo et al (2016).1
Corroborando a hipótese de aglomeração econômico-populacional (Ottaviano e Thisse, 2004), a Tabela 1 revela que o PIB per capita médio dos municípios brasileiros mais populosos (faixa 6) é sempre superior ao das faixas inferiores. Embora a renda per capita das localidades de menor porte (faixa 1) seja reduzida, ela não é a menor entre as faixas. É possível que essa dificuldade em atingir níveis mais elevados decorra, em parte, da forte dependência desse grupo do setor público.
Tabela 1 Média do PIB per capita municipal em diferentes faixas populacionais (R$ milhar, valores constantes de 2010)
| Faixa | (2) | (3) | (4) | (5) | (6) | |
|---|---|---|---|---|---|---|
| População | Até 5mil | 5-25mil | 25-50mil | 50-100mil | 100-500mil | Mais de 500mil |
| N°. Municípios (%) | 1300 (23.4) | 2976 (53.5) | 685 (12.3) | 324 (5.8) | 242 (4.3) | 38 (0.7) |
| PIB 2000 | 11.11 | 9.55 | 11.57 | 13.90 | 18.39 | 23.20 |
| PIB 2010 | 12.79 | 11.08 | 13.37 | 15.58 | 21.96 | 26.31 |
| PIB 2020 | 16.25 | 13.34 | 15.43 | 16.76 | 20.63 | 22.15 |
| Cresc. 2000-2020 | 46.3% | 39.6% | 33.3% | 20.5% | 12.2% | -4.5% |
Fonte: Elaboração própria com base nas contas regionais do IBGE (IPEADATA, 2023).
Segundo as contas regionais do IBGE (IPEADATA, 2023), a participação do setor público no PIB per capita municipal de 2020 nas seis faixas apresentadas (Tabela 1), foi de 22.6%, 21.2%, 17.1°%, 15.4%, 13.1°% e 13.5%, respectivamente. Assim, a transição para faixas superiores exigiria menor dependência pública. Apesar disso, o crescimento econômico dos municípios menores tem sido mais acentuado que o dos grandes centros, sugerindo um processo de convergência da renda per capita entre os mais ricos e os mais pobres.2
Logo, assumindo que os municípios mais ricos possuem maior porte populacional (Tabela 1) e que as economias dos municípios mais pobres demandam estímulos distintos das mais ricas (Veríssimo e Saiani, 2019), é razoável supor que os fatores associados ao crescimento econômico municipal, bem como seus impactos, variem de acordo o porte populacional considerado.
Dentre os fatores supracitados, a literatura indica que o crescimento econômico (Δy) dependeria da própria renda inicial (y 0 ), cujo sinal negativo indicaria convergência entre ricos e pobres (Mankiw, Romer e Weil, 1992), das demais dotações prévias de recursos e de suas respectivas melhorias (Sokoloff e Engerman, 2000; Ferreira e Cruz, 2010).
Estas dotações incluem: a) qualidade da educação (EDUC) e da saúde (SAU), que podem aumentar a produtividade laboral e reduzir o absenteísmo (Mankiw, Romer e Weil, 1992; Andrade e Serra 1998; Miller e Upadhyay, 2000; Firme e Simão Filho, 2014); b) criminalidade (CRIM), cujo aumento tende a inibir empreendimentos locais (Divino e Silva Junior 2012; Diallo, 2018; Cox, North e Weingast, 2019); c) infraestrutura (INFR), que pode minimizar certos custos de produção (Andrade e Serra 1998; Esfahani e Ramírez, 2003); d) demanda local (DL), que tende a atrair empresas interessadas na mão-de-obra e no consumo potencial, e pessoas, em busca de emprego (Andrade e Serra 1998; Fujita, Krugman e Mori,1999); e) viés produtivo (Kaldor, 1966; Andrade e Serra 1998), onde sustenta-se que a indústria (IND) seria crucial às cidades mais pobres, enquanto o setor de serviços (SER) promoveria o crescimento das mais ricas (Veríssimo e Saiani, 2019). A dependência da administração pública (ADM), que supõe-se um entrave, também foi avaliada; f) concentração do mercado de trabalho (CMT) (Fochezatto e Valentini 2010; Sarmento e Nunes, 2015), que pode elevar os ganhos de escala (Madiedo et al, 2012) ou reduzir os encadeamentos produtivos (Miller e Blair, 2009); g) fatores demográficos, segundos os quais populações mais jovens (JOID) seriam menos experientes/produtivas e mais propensas à rotatividade no emprego (Crenshaw, Ameen, e Christenson, 1997; Mankiw, 2010).
A atividade econômica também poderia ser estimulada por meio da demanda, via gastos públicos correntes (GC) e de capital (GK) (Barro, 1990; Lin, 1994; Andrade e Serra 1998; Divino e Silva Junior 2012; Taylor et al, 2012) e/ou crédito bancário (CRED) (Kroth e Dias, 2006; Galeano e Feijó, 2012). Ademais, seria influenciada tanto pelo clima (CLIM), que "could have helped determine where industrialization would first take place, facilitating the accumulation of human capital and savings from agriculture" (Masters e Mcmillan, 2001, p.182), quanto pela localização em relação aos grandes centros (LOC) (Divino e Silva Junior 2012; Firme, 2022), onde acredita-se que o aumento da distância seria prejudicial, pois minimizaria as externalidades positivas provenientes dos grandes centros (Perroux, 1950; Hirschman; 1958).
Com base nos autores mencionados nesta seção, infere-se que o crescimento econômico (Δy) depende das seguintes variáveis, cujos efeitos esperados estão indicados em sobrescrito:3
Na prática, alguns destes propulsores e inibidores do crescimento distribuem-se de forma heterogênea. As cidades pequenas, devido à baixa diversificação produtiva, tendem a ser mais suscetíveis a choques externos (Penrose, 1979), dependentes de cargos públicos (Carvalho, 2009) e da oferta de bens e serviços provenientes de cidades maiores (França). Embora careçam de incentivos públicos (Thirlwall e Pacheco-López, 2017), Juanico (1977) e Fernandes e Correia (2018) sustentam que essas localidades não são atrativas ao Estado. Apesar de as cidades grandes apresentarem maiores desafios de governança (Reis et al 2013), Sousa e Ramos (1999) revelam que os gastos públicos nos municípios menores tendem a ser menos eficientes, reforçando a acumulação circular proposta por Myrdal (1957). Ainda assim, as cidades pequenas costumam ser mais seguras, menos poluídas e podem apresentar melhores níveis de saúde e bem-estar (Jerrett et al, 2009; Oliveira et al, 2017; Pinheiro e Firme, 2022).
3. METODOLOGIA E BASE DE DADOS
A seção anterior mostrou que o crescimento econômico, entre os períodos analisados (0 e t), de um município i qualquer [Δy i0t = ln(y it /y i0 )], depende de sua renda inicial (yi0), das dotações prévias de recursos (DOT i0 ), das alterações nessas dotações (ΔDOT m ), bem como de fatores invariantes no tempo, como a temperatura (TEMP i ), a precipitação (PREC i ) e a localização relativa (LOCi). Portanto:
Onde DOT i0 é uma matriz com i-observações por k-variáveis, sendo elas: EDUC 0 = nível educacional; SAU 0 = nível de saúde; CRIM 0 = criminalidade; INFR 0 = infraes-trutura; DL 0 = demanda local; IND0, SER 0 e ADM 0 = peso da indústria, serviços e setor público na produção; CMT 0 = concentração do mercado de trabalho; JOID 0 = proporção de jovens/idosos; GK 0 = gasto em capital; GC 0 = gasto corrente; CRED0 = uso de crédito bancário. Ademais, ADOT i,0t = ln(DOT it /DOT i0 ).4 Operacionalmente, a equação 2 torna-se:
Sendo ß i ,, k , os coeficientes de impacto global associados às k variáveis explicativas e e it é um termo de erro aleatório. Logo, visando analisar os ß impactos, descritos na Equação 3, em locais com diferentes portes populacionais, inseriu-se termos interativos (Greene, 2002), que consistem na multiplicação das variáveis explicativas por dummies (binárias), referentes às 6 faixas populacionais da Tabela 1.5 Assim, incluindo todas as variáveis explicativas em uma matriz X i,0t , de dimensão ,=11010 por k =30 variáveis (exceto a constante), e criando 6 dummies de faixa populacional (i.e.: D5, D25, D50, D100, D 500 e Dmáx),6 o modelo para diferentes portes se torna:
Na equação 4, os coeficientes ß2...31 medem o efeito específico de cada variável X
i,0
(inserida em X,0), sobre o crescimento (Δy) dos municípios com até 5 mil habitantes (análise análoga aos demais portes populacionais). As equações 3 e 4 podem ser estimadas pelo método Pooled Ordinary Least Squares (POLS), aplicando-se o teste de Breusch-Pagan (1980) para verificar se existe algum efeito não observado,
c
i
,
constante no tempo (como cultura, preferências ou clima.), afetando os resíduos. Se
H
0
:σ
2
c
=0,
o POLS é o mais indicado. Caso contrário (
σ
2
c# 0), estima-se os modelos de efeitos fixos (EF) e aleatórios (EA) usando o teste de Hausman (1978) para definir se
c
t
causa viés nos
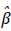 parâmetros.7 Aceitando-se
parâmetros.7 Aceitando-se
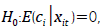 , EF e EA serão consistentes, porém EA será mais eficiente. Do contrário, apenas EF será consistente (Wooldridge, 2010b). Optou-se por estimar os modelos EF e EA antes do POLS. Assim, se o teste de Hausman (1978) indicar que apenas EF é consistente, não haveria a necessidade do POLS. Em todos os casos, usou-se a matriz robusta de White (1980), para contornar problemas de heterocedasticidade.
, EF e EA serão consistentes, porém EA será mais eficiente. Do contrário, apenas EF será consistente (Wooldridge, 2010b). Optou-se por estimar os modelos EF e EA antes do POLS. Assim, se o teste de Hausman (1978) indicar que apenas EF é consistente, não haveria a necessidade do POLS. Em todos os casos, usou-se a matriz robusta de White (1980), para contornar problemas de heterocedasticidade.
Como o crescimento de um município brasileiro pode influenciar o de seus vizinhos e vice-versa (Firme, 2022), buscou-se controlar a dependência espacial associada às Equações 3 e 4 (Elhorst, 2014).8 Para tanto, foi utilizada uma matriz de contiguidade espacial "rainha" (W)9 para estimar o modelo Spatial Autoregressive Confused (SAC), que mede o efeito espacial na variável dependente (WΔy i,0t ) e no termo de erro (W ξit ).10 Formalmente:
a) Modelo SAC com efeitos globais é representado por:
b) Modelo SAC com efeitos por porte municipal introduz termos específicos para cada faixa populacional:
As equações 5 e 6 foram estimadas por Quasi Máxima-Verossimilhança (QMV), com base no método de efeitos fixos espacial (EFE), de Lee e Yu (2010), e no modelo de efeitos aleatórios espacial (EAE), proposto por Kapoor, Kelejian e Prucha (2007). Em ambos os casos, o efeito total de
x
k
depende do seu impacto inicial
(ß
k
)
e do efeito multiplicador gerado pela vizinhança. Assim, com base na matriz de efeitos parciais
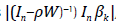 , onde
I
n
é uma matriz identidade, obtém-se o efeito direto
(ED
= média da diagonal principal), indireto
(EI
= média dos demais elementos) e total, ET=
ED+EI,
oriundo de
x
k
(Lesage e Pace, 2009). Novamente, usou-se o teste de Hausman (1978) para definir entre EFE ou EAE.
, onde
I
n
é uma matriz identidade, obtém-se o efeito direto
(ED
= média da diagonal principal), indireto
(EI
= média dos demais elementos) e total, ET=
ED+EI,
oriundo de
x
k
(Lesage e Pace, 2009). Novamente, usou-se o teste de Hausman (1978) para definir entre EFE ou EAE.
3.1. Base de Dados
Com objetivo de mensurar os efeitos de fatores associados ao crescimento econômico em municípios com diferentes portes populacionais, este estudo utilizou um painel espacial balanceado com dados de 5.505 municípios brasileiros, referente aos períodos de 2000-2010 e 2010-2020. As estimativas contaram com , = (5505 * 2] = 11010 observações e incluiu as seguintes variáveis:
● Crescimento econômico (Δy i,0t } (variável dependente): utilizou-se o PIB per capita municipal, em R$ milhar (preços de 2010), do Instituto Brasileiro de Geografia e estatística - IBGE (IPEADATA, 2023). Formalmente: Δ yi,0t = ln(y i,t /y i,0 )..
● Renda inicial (y0}: trata-se do PIB per capita, em R$ milhar/2010, do ano inicial ao crescimento econômico. Logo, Y 0= Y 2000 se Δy 2000-2010 e Y 0 = Y 2010 quando Δy 2010-2020 (IPEADATA, 2023).
● Educação inicial (EDUC 0 } e suas alterações (ΔEDUC}: usou-se o percentual de trabalhadores, registrados na Relação Anual de Informações Sociais - RAIS (2023), com ensino médio completo.
● Condição de saúde (SAU0 e Δ SAU): trata-se da mortalidade por causas evitáveis, em indivíduos de 5-74 anos, a cada 100 mil habitantes (DATASUS, 2023). Segundo o Ministério da Saúde - MS (2023a), tais óbitos seriam passíveis de prevenção e refletiriam um sistema de saúde incapaz de atender às necessidades locais. A fim de evitar valores faltantes (missing values), usou-se a média dos óbitos entre 1996-2000, 2006-2010 e 2016-2020.11
● Criminalidade (CRIM 0 e Δ ACRIM ): trata-se do número médio de homicídios, a cada 100 mil habitantes, nos últimos 10 anos (IPEADATA, 2023).
● Infraestrutura (INFR 0 e Δ INFR): usou-se a mortalidade (a cada 100 mil habitantes) ocasionada por doenças típicas da falta de saneamento básico (Habitat Brasil, 2023), referentes às categorias AA00 a AA09 da CID-10 (DATASUS, 2023).
● Demanda Local (DL0 e ΔDL): refere-se à divisão da população municipal (POP it ), mensurada via estimativas do IBGE (IPEADATA, 2023), pela média de sua respectiva vizinhança ( WPOPit). Para obter WPOP it , usou-se o software GEODA (Almeida, 2012) e uma matriz espacial rainha (W). Assim, DLt= 0 = (POPit=0/WPOPit=0}.
● Viés produtivo (IND0, SER0 e ADM0) e suas alterações (AIND, Δ SER e ΔADM): usou-se a participação (%) da indústria (IND), dos serviços (SER) e da administração pública (ADM) no PIB municipal, disponibilizados nas contas regionais do IBGE (IPEADATA, 2023).
● Concentração do mercado de trabalho
(CMT
0
e
Δ
CMT):
trata-se do índice Herfindahl-Hirschman -
IHH
it
(Sarmento e Nunes, 2015), que usa a distribuição dos trabalhadores (RAIS, 2023), entre os
n
= 25 subsetores do IBGE e o total de empregados no município (i) no ano (t), ou seja,
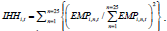 . Logo,
IHH
i,t
= 1, se só 1 setor empregar, e
IHH
it
= 0.04, se todos empregarem a mesma quantidade.
. Logo,
IHH
i,t
= 1, se só 1 setor empregar, e
IHH
it
= 0.04, se todos empregarem a mesma quantidade.
● Relação jovens/idosos (JOID 0 e Δ JOID): trata-se da proporção de jovens (0-14 anos) frente aos idosos (65 anos ou mais), ou seja, JOID 0 =(total jovens 0 /total ,dosos 0 ). A população, por faixa etária, é calculada pelo Ministério da Saúde (DATASUS, 2023).
● Incentivos públicos (GK 0 e GC0) e suas oscilações (AGK e ΔGC): refere-se ao valor per capita municipal alocado em gasto corrente (GC) e de capital (GK), ambos convertidos em R$/2010 via INPC. Para evitar missing values, usou-se a média dos valores disponíveis nos últimos 5 anos (Ministério da Fazenda - IPEADATA, 2023).
● Fatores invariantes no tempo: considerou-se a média anual de temperatura -TEMP (em graus centígrados, °C) e precipitação - PREC (em milímetros por mês, mm/mês), 12 bem como a localização relativa à capital estadual -LOC (distância em quilômetros, Km), disponíveis no IPEADATA (2023).
A Tabela 2 contém os sinais esperados e as estatísticas descritivas dos dados utilizados.
Tabela 2 Sinais esperados e estatísticas descritivas dos dados
| SIGLA | Medida | Sinal. Esp. | Média | Des. Pad. | Mínimo│Máximo |
|---|---|---|---|---|---|
| ∆y | % | n.a. | 13.10% | 32.78% | -166.77%│326.49% |
| y 0 | R$ milhar (2010) | - | 11.65 | 12.84 | 2.13│282.69 |
| EDUC 0 | % | + | 31.27% | 15.75% | 0.00%│100.00% |
| ∆EDUC | % | + | 11.71% | 15.03% | -90.43│90.33% |
| SAU 0 | p/ cada 100 mil hab. | - | 297.94 | 108.34 | 9.7│717.90 |
| ∆SAU | % | - | 18.59% | 31.35% | -93.73%│276.46% |
| CRIM 0 | p/ cada 100 mil hab. | - | 22.80 | 15.26 | 0.00│197.55 |
| ∆CRIM | % | - | 17.00% | 44.33% | -190.87%│207.77% |
| ∆y | % | n.a. | 13.10% | 32.78% | -166.77%│326.49% |
| INFR 0 | p/ cada 100 mil hab. | - | 13.08 | 12.28 | 0.00│124.61 |
| ∆INFR | % | - | -12.06% | 38.45% | -245.41%│182.04% |
| DL 0 | índice | + | 1.12 | 2.58 | 0.01│55.63 |
| ∆DL | % | + | -1.47% | 11.08% | -124.75%│92.84% |
| IND 0 | % | + | 13.81% | 13.97% | 1.07%│89.71% |
| ∆IND | % | + | 0.33% | 9.81% | -75.31%│88.29% |
| SER 0 | % | + | 38.34% | 13.72% | 6.41%│89.21% |
| ∆SER | % | + | -6.74% | 12.65% | -68.10%│41.70% |
| ADM 0 | % | - | 27.44% | 15.22% | 1.41%│44.08% |
| ∆ADM | % | - | 5.76% | 12.00% | -65.52%│50.27% |
| CMT 0 | índice | +/- | 0.40 | 0.26 | 0.06│1.00 |
| ∆CMT | % | +/- | -9.79% | 29.50% | -173.77%│168.50% |
| JOID 0 | índice | - | 4.70 | 3.02 | 1.10│59.96 |
| ∆JOID | % | - | -47.63% | 15.07% | -170.34%│33.33% |
| GK 0 | R$ (2010) | + | 164.10 | 164.84 | 0.00│6654.11 |
| ∆GK | % | + | 33.63% | 82.58% | -557.70%│842.53% |
| GC 0 | R$ (2010) | + | 788.70 | 705.71 | 0.00│48889.63 |
| ∆GC | % | + | 47.02% | 57.17% | -1699.19%│796.00% |
| CRED 0 | R$ (2010) / mil hab. | + | 451.74 | 1214.46 | 0.00│68448.68 |
| ∆CRED | % | + | 38.45% | 206.70% | -1005.73%│1251.36% |
| TEMP | Graus Celsius (°C) | ? | 22.83 | 3.02 | 14.00│28.04 |
| PREC | Milímetros/mês | ? | 115.90 | 36.91 | 28.87│282.43 |
| LOC | Quilômetros | - | 253.19 | 163.62 | 0.00│1476.28 |
Fonte: elaboração própria a partir dos dados da pesquisa (2023).
4. ANÁLISE DOS RESULTADOS
Os modelos de efeitos aleatórios (EA) e fixos (EF), estimados sem controles espaciais e associados às Equações 3 (efeito global) e 4 (efeito por porte populacional), embora não reportados,13 obtiveram R2 Within de 0.78 (EA-Global), 0.80 (EA-Porte), 0.88 (EF-Global) e 0.89 (EF-Porte), o que indica que as variáveis selecionadas explicam grande parte do crescimento econômico dos municípios brasileiros entre 2000-2020. Em todos os casos, o teste de Hausman (1978) apontou a superioridade do modelo de EF em relação ao de EA. Após incluir a dependência espacial na variável dependente (W_ε) e no termo de erro (W_ΔY), conforme as Equações 5 e 6, verificou-se que ambos os efeitos espaciais são estatisticamente significativos, até mesmo a 1%. Além disso, o modelo com termos interativos (cujo AIC é menor que o da especificação global), estimado via EF, revelou-se superior (Tabela 3).
Tabela 3 Impactos associados ao crescimento econômico em diferentes faixas populacionais: com controles espaciais
| Modelo>a) | EA b) EF | c) Modelo de Efeitos Aleatórios (EA) | d) Modelo de Efeitos Fixos (EF) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Faixas > | Todas | até 5 | 5-25 | 25-50 | 50-100 | 100-500 | 500+ | até 5 | 5-25 | 25-50 | 50-100 | 100-500 | 500+ | |
| y 0 | -0.36*** | -1.15*** | -0.42*** | -0.37*** | -0.32*** | -0.34*** | -0.32*** | -0.55*** | -1.15*** | -1.19*** | -1.05*** | -1.09*** | -1.29*** | -1.24*** |
| EDUC 0 | 0.03* | 0.11*** | 0.12*** | 0.03 | -0.04 | -0.21*** | -0.32*** | 0.22 | 0.18*** | 0.08** | 0.20** | 0.00 | -0.06 | 0.62 |
| ∆EDUC | 0.06*** | 0.08*** | 0.10*** | 0.05*** | -0.01 | 0.08 | -0.01 | 0.26 | 0.13*** | 0.07*** | 0.06 | 0.17 | 0.03 | 0.87 |
| SAU 0 | -0.02** | 0.12*** | -0.01 | -0.01 | 0.02 | 0.08** | -0.04 | 0.37 | 0.09*** | 0.11*** | 0.10* | 0.19** | 0.21 | -0.13 |
| ∆SAU | 0.01 | 0.07*** | 0.01 | 0.02* | 0.03 | 0.01 | -0.07 | -0.46 | 0.04** | 0.08*** | 0.07 | 0.08 | 0.19 | -0.47 |
| CRIM 0 | 0.01*** | 0.01 | 0.01 | 0.01** | -0.01 | -0.04*** | -0.00 | -0.21** | -0.00 | 0.04*** | -0.00 | -0.04 | 0.03 | -0.03 |
| ∆CRIM | -0.01 | 0.01 | 0.01 | -0.01 | -0.02 | -0.03** | 0.04* | -0.07 | 0.00 | 0.02** | -0.01 | -0.03 | 0.02 | 0.03 |
| INFR 0 | 0.00 | -0.01 | -0.00 | 0.01*** | -0.00 | -0.01 | 0.02 | -0.05 | -0.06 | -0.01 | -0.03* | -0.02 | -0.06* | 0.13 |
| ∆INFR | 0.01** | -0.01 | 0.01 | 0.01 | 0.01 | 0.01 | 0.00 | -0.05 | -0.07* | -0.01 | -0.01 | -0.00 | -0.04* | 0.09 |
| DL 0 | -0.00 | -0.19*** | -0.01*** | 0.01* | -0.01 | -0.00 | 0.00 | -0.02 | -0.34*** | -0.15*** | 0.21** | -0.07 | 0.32 | -0.01 |
| ∆DL | -0.19*** | -0.25*** | -0.20*** | -0.21*** | -0.03 | -0.15** | -0.10 | -0.05 | -0.30*** | -0.24*** | 0.33** | 0.22 | 0.58 | 0.49 |
| IND 0 | 0.27*** | 0.98*** | 0.37*** | 0.24*** | 0.22*** | 0.03 | 0.21 | -1.34 | 1.04*** | 0.92*** | 1.27*** | 1.17*** | 3.22*** | 4.98 |
| ∆IND | 0.85*** | 0.83*** | 0.89*** | 0.83*** | 0.85*** | 0.61*** | 1.26*** | -5.66 | 0.81*** | 0.78*** | 1.12*** | 1.03*** | 2.38*** | -1.99 |
| SER 0 | 0.15*** | -0.12** | 0.05 | 0.11*** | 0.17*** | 0.11 | 0.30 | -1.86 | -0.07 | -0.14** | 0.45*** | 0.68*** | 2.39*** | 4.17 |
| ∆SER | -0.15*** | 0.06 | -0.19*** | -0.21*** | -0.01 | 0.16 | 0.77*** | -6.12 | 0.16** | -0.02 | 0.43*** | 0.64*** | 1.82*** | -2.19 |
| ADM 0 | -1.20*** | -3.40*** | -1.38*** | -1.25*** | -1.26*** | -1.40*** | -1.14*** | -3.32 | -3.40*** | -3.47*** | -3.44*** | -4.15*** | -3.88*** | 0.60 |
| ∆ADM | -2.66*** | -2.88*** | -2.66*** | -2.65*** | -2.88*** | -3.35*** | -3.60*** | -9.43 | -2.90*** | -2.82*** | -2.96*** | -3.57*** | -3.08*** | -5.01 |
| CMT 0 | 0.06*** | 0.05*** | 0.07*** | 0.04*** | 0.05*** | 0.05** | 0.02 | 0.24 | 0.02 | 0.07*** | 0.02 | 0.16*** | 0.15 | 0.68 |
| ∆CMT | 0.08*** | 0.06*** | 0.07*** | 0.08*** | 0.07*** | 0.07*** | 0.10** | 0.52 | 0.04*** | 0.06*** | 0.08*** | 0.12*** | 0.10 | 0.78 |
| JOID 0 | 0.04*** | -0.20*** | 0.02*** | 0.05*** | 0.04*** | 0.08*** | 0.06** | 0.34*** | -0.22*** | -0.21*** | -0.08** | -0.01 | -0.01 | 0.20 |
| ∆JOID | 0.02 | -0.07*** | 0.02 | 0.02 | 0.10** | -0.00 | 0.21** | 0.53 | -0.14*** | -0.06* | 0.10 | -0.00 | 0.16 | 0.02 |
| GK 0 | 0.05*** | 0.03*** | 0.05*** | 0.04*** | 0.04*** | 0.02 | 0.06*** | -0.02 | 0.05*** | 0.00 | 0.04** | -0.00 | 0.02 | -0.02 |
| ∆GK | 0.04*** | 0.02*** | 0.04*** | 0.03*** | 0.05*** | 0.02 | 0.08*** | -0.01 | 0.03*** | 0.00 | 0.04*** | 0.00 | 0.01 | -0.02 |
| GC 0 | 0.05*** | 0.11*** | 0.03*** | 0.07*** | 0.04** | 0.06* | 0.09*** | 0.20 | 0.04*** | 0.17*** | 0.18*** | 0.27*** | 0.23*** | 0.44 |
| ∆GC | 0.06*** | 0.07*** | 0.03*** | 0.09*** | 0.04*** | 0.10*** | 0.09*** | 0.07 | 0.02*** | 0.12*** | 0.10*** | 0.24*** | 0.15*** | 0.15 |
| CRED 0 | -0.00*** | -0.00 | -0.00 | 0.00 | -0.01*** | -0.01 | -0.02 | 0.02 | 0.00 | -0.00 | 0.00 | 0.06*** | 0.08** | 0.02 |
| ∆CRED | 0.00 | -0.00 | 0.00 | 0.00* | -0.00 | 0.02 | 0.03 | 0.02* | 0.00 | -0.00 | 0.00 | 0.05*** | 0.05 | 0.01 |
| TEMP | 0.15*** | EXC. | 0.23*** | 0.12*** | 0.14*** | 0.17*** | 0.09 | 0.09 | EXC. | EXC. | EXC. | EXC. | EXC. | EXC. |
| PREC | -0.02* | EXC. | -0.01 | -0.01 | 0.01 | -0.04* | 0.04 | -0.07 | EXC. | EXC. | EXC. | EXC. | EXC. | EXC. |
| LOC | 0.01** | EXC. | 0.00 | -0.00 | 0.00 | -0.01 | 0.01 | -0.02 | EXC. | EXC. | EXC. | EXC. | EXC. | EXC. |
| CTE | 0.11 | EXC. | 0.13 | EXC. | ||||||||||
| W_∆Y | -0.02*** | -0.01*** | -0.02*** | -0.01*** | ||||||||||
| W_ε | 0.10*** | 0.10*** | 0.10*** | 0.10*** | ||||||||||
| AIC | -9377.5 | -8440.9 | -9734.6 | -8715.7 | ||||||||||
Notas: a) p-valor. *<0.10; **<0.05; ***<0.01; b) faixas populacionais em milhar; c) os efeitos das demais variáveis dependem do efeito multiplicador gerado por W_ΔY (ver Tabela 4).
Fonte: elaboração própria com base no software STATA e nos dados coletados (2023).
Como o estimador EF elimina as variáveis fixas no tempo, os efeitos de tais variáveis só podem ser avaliados via EA, conforme a Tabela 3. Nesse caso, municípios localizados em regiões mais quentes (TEMP), com menor precipitação (PREC) e mais afastados das capitais estaduais (LOC), apresentaram maior crescimento econômico (modelo "a"). Para Masters e Mcmillan (2001), climas temperados - caracterizados por invernos frios e úmidos e verões quentes e secos - favorecem a lavoura e a acumulação de capital físico e humano, o que explicaria a concentração de renda nas regiões Sul e Sudeste do Brasil (IBGE/Clima, 2023). Considerando a existência de convergência de renda (confirmada na Tabela 4) e o fato de que os municípios mais pobres, com crescimento mais acelerado, se concentram nas áreas mais quentes, como o Nordeste, é esperado um sinal positivo associado à TEMP e negativo em PREC. As estimativas com termos interativos (modelo c) indicam que temperaturas elevadas podem favorecer o crescimento de municípios com até 100 mil habitantes, enquanto a precipitação tem efeito apenas em cidades com 50-100 mil habitantes.14 Contrariando Perroux (1950) e Hirschman (1958), mas corroborando Pinheiro e Firme (2022), observou-se que a proximidade em relação às capitais estaduais tende a prejudicar o crescimento econômico (modelo "a"). Contudo, esse efeito não foi estatisticamente relevante em nenhuma das faixas populacionais testadas.
Após o cálculo dos efeitos diretos (ED) e totais (ET) do modelo EF com termos interativos (Tabela 4), verificou-se que, das 27 variáveis analisadas, 20 apresentaram impactos significativos em municípios com até 25 mil habitantes, 18 nas cidades com 25 a 50 mil habitantes, 14 nas de 50 a100 mil, 12 nas de 100 a 500 mil, e apenas uma variável afetaria localidades com mais de 500 mil habitantes. Portanto, a efetividadedas políticas voltadas ao crescimento econômico parece diminuir à medida que o porte populacional aumenta.
Em consonância com Mankiw, Romer e Weil, 1992, os resultados confirmam a existência de convergência de renda (i.e.: redução das desigualdades) entre as faixas populacionais (sinal negativo/significativo de y0). Ademais, tanto níveis educacionais mais elevados (EDUC 0 ) quanto melhorias na educação local (ΔEDUC) mostraram-se relevantes para municípios com até 50 mil habitantes. No caso da saúde (SAU 0 e ΔSAU), notou-se uma relação positiva entre a mortalidade por causas evitáveis e o crescimento econômico (Δy) nas cidades com até 100 mil habitantes. Como as cidades menores e/ou mais pobres possuem elevada subnotificação de óbitos (Miranda et al, 2023), é possível que melhorias na saúde destes locais, ao reduzir tais subnotificações, estimulem Ay ao mesmo tempo em que aumentam as taxas de mortalidade (subestimadas, até então).
Tabela 4 Impactos diretos populacionais e totais associados ao crescimento econômico em diferentes faixas
| População | Efeitos Diretos│Totais | |||||
|---|---|---|---|---|---|---|
| Variáveis | até 5 mil | 5-25 mil | 25-50 mil | 50-100 mil | 100-500 mil | + de 500 mil |
| y 0 | -1.15***│-1.09*** | -1.19***│-1.14*** | -1.06***│-1.00** | -1.09***│-1.04*** | -1.29***│-1.23*** | -1.24***│-1.18*** |
| EDUC 0 | 0.18***│0.17*** | 0.08**│0.07** | 0.20**│0.19** | 0.00│0.00 | -0.06│-0.05 | 0.62│0.59 |
| ∆EDUC | 0.13***│0.12*** | 0.07***│0.06*** | 0.06│0.05 | 0.17│0.16 | 0.03│0.02 | 0.87│0.83 |
| SAU 0 | 0.09***│0.08*** | 0.11***│0.11*** | 0.10*│0.09* | 0.19**│0.18** | 0.21│0.20 | -0.13│-0.13 |
| ∆SAU | 0.04**│0.04** | 0.08***│0.08*** | 0.07│0.07 | 0.08│0.08 | 0.19│0.18 | -0.47│-0.45 |
| CRIM 0 | 0.00│0.00 | 0.04***│0.04*** | 0.00│0.00 | -0.04│-0.04 | 0.03│0.03 | -0.03│-0.03 |
| ∆CRIM | 0.00│0.00 | 0.02**│0.02** | -0.01│-0.01 | -0.03│-0.03 | 0.02│0.02 | 0.03│0.03 |
| INFR 0 | -0.06│-0.05 | -0.01│-0.01 | -0.03*│-0.03* | -0.02│-0.02 | -0.06*│-0.06* | 0.13│0.12 |
| ∆INFR | -0.07*│-0.06* | -0.01│-0.01 | -0.01│-0.01 | 0.00│0.00 | -0.04*│-0.04* | 0.09│0.08 |
| DL 0 | -0.34***│-0.33*** | -0.15***│-0.14*** | 0.21**│0.20** | -0.07│-0.06 | 0.32│0.31 | -0.01│-0.01 |
| ∆DL | -0.30***│-0.29*** | -0.24***│-0.22*** | 0.33**│0.31** | 0.23│0.21 | 0.58│0.56 | 0.49│0.47 |
| IND 0 | 1.04***│0.99*** | 0.92***│0.88*** | 1.27***│1.21*** | 1.17***│1.11*** | 3.22***│3.07*** | 4.98│4.74 |
| ∆IND | 0.81***│0.77*** | 0.78***│0.74*** | 1.12***│1.07*** | 1.03***│0.98*** | 2.38***│2.27*** | -1.99│-1.89 |
| SER 0 | -0.07│-0.07 | -0.14**│-0.14** | 0.45***│0.43*** | 0.68***│0.65*** | 2.39***│2.28*** | 4.17│3.97 |
| ∆SER | 0.16**│0.15** | -0.02│-0.02 | 0.43***│0.41*** | 0.64***│0.61*** | 1.82***│1.73*** | -2.19│-2.09 |
| ADM 0 | -3.40***│-3.24*** | -3.48***│-3.31*** | -3.44***│-3.27*** | -4.15***│-3.95*** | -3.88***│-3.69*** | 0.60│0.57 |
| ∆ADM | -2.90***│-2.76*** | -2.83***│-2.69*** | -2.96***│-2.82*** | -3.57***│-3.40*** | -3.09***│-2.94*** | -5.02│-4.78 |
| CMT 0 | 0.02│0.02 | 0.07***│0.06*** | 0.02│0.02 | 0.16***│0.15*** | 0.15│0.15 | 0.68│0.65 |
| ΔCMT | 0.05***│0.04*** | 0.06***│0.06*** | 0.08***│0.07*** | 0.12***│0.12*** | 0.10│0.10 | 0.78│0.74 |
| JOID 0 | -0.22***│-0.21*** | -0.21***│-0.20*** | -0.08**│-0.07** | -0.01│-0.01 | -0.01│-0.01 | 0.20│0.19 |
| ∆JOID | -0.14***│-0.13*** | -0.06*│-0.05* | 0.10│0.10 | 0.00│0.00 | 0.16│0.15 | 0.02│0.02 |
| GK 0 | 0.05***│0.05*** | 0.00│0.00 | 0.04**│0.03** | 0.00│0.00 | 0.02│0.02 | -0.02│-0.02 |
| ∆GK | 0.03***│0.03*** | 0.00│0.00 | 0.04***│0.04*** | 0.00│0.00 | 0.01│0.01 | -0.02│-0.02 |
| GC 0 | 0.04***│0.03*** | 0.17***│0.16*** | 0.18***│0.17*** | 0.27***│0.26*** | 0.23***│0.22*** | 0.44│0.42 |
| ∆GC | 0.02***│0.02*** | 0.12***│0.12*** | 0.10***│0.10*** | 0.24***│0.23*** | 0.15***│0.15*** | 0.15│0.14 |
| CRED 0 | 0.00│0.00 | 0.00│0.00 | 0.00│0.00 | 0.06***│0.06*** | 0.08**│0.08** | 0.02│0.02 |
| ∆CRED | 0.00│0.00 | 0.00│0.00 | 0.00│0.00 | 0.05***│0.05*** | 0.05│0.04 | 0.01│0.01 |
Fonte: elaboração própria com base no software STATA e nos dados coletados (2023).
A criminalidade (CRIM 0 e Δ CRIM) apresentou significância estatística apenas nos municípios com 5 a 25 mil habitantes, exibindo sinal contrário ao esperado. Para Oliveira (2008), a relação entre crime e crescimento econômico (Δy) tende a ser negativa somente se o crescimento for capaz de reduzir as desigualdades, ou seja, quando a economia é impulsionada, principalmente, pelos segmentos mais pobres. Além disso, como apontado na Seção 2, a falta de infraestrutura (INFR 0 e Δ INFR), especialmente relacionada ao saneamento básico, constitui um obstáculo ao crescimento econômico, afetando municípios com até 5 mil, 25 a 50 mil e entre 100 e 500 mil habitantes (Tabela 4).
Em municípios com até 25 mil habitantes, ter vizinhos de menor porte populacional pode prejudicar o crescimento econômico (sinais negativos de DL 0 e ADL). Conforme Penrose (1979), cidades pequenas costumam apresentar baixa diversificação produtiva e maior dependência de locais mais populosos (França, 2021); assim, a ausência de grandes centros, nas proximidades, limita o dinamismo econômico local. Essa dependência se inverte nos municípios de 25 a 50 mil habitantes, que passam a atuar como fornecedores de bens e serviços às localidades menores, e perde significância nas faixas populacionais mais elevadas (Tabela 4).
Como exceção dos municípios com mais de 500 mil habitantes, o viés produtivo manteve-se estatisticamente significativo entre todas as faixas populacionais. Assim, em consonância com Veríssimo e Saiani, (2019), nota-se que o crescimento econômico (Δy) tende a ser maior em localidades com estrutura produtiva voltada à indústria (IND0 e Δ IND) e, em menor escala, ao setor de serviços (5ER0 e ASER). Já a dependência da administração pública ( Δ DM 0 e ΔADM), como discutido na Seção 2, mostra-se nociva ao desempenho econômico. Ademais, a concentração de trabalhadores (CMT0 e Δ CMT) em poucos setores revela-se vantajosa para municípios com até 100 mil habitantes (Tabela 4), possivelmente por estimular a especialização produtiva local (Madiedo et al, 2020).
Conforme sugerido na Seção 2, populações mais jovens (JOID 0 e Δ JOID), talvez por demandarem muitos serviços públicos e contribuírem pouco para a atividade econômica (Mincer, 1984), inibiriam o crescimento econômico.15 Este problema seria relevante em municípios com até 50 mil habitantes. Já os gastos públicos em bens de capital (GK0 e Δ GK) mostraram-se promissores às estes locais. Os gastos correntes (GC 0 e Δ GC), por sua vez, estimulariam o crescimento de todas as faixas populacionais.16 Este efeito positivo dos gastos públicos, independente do déficit e/ou da pressão sobre os juros, também foi obtido por Taylor et al (2012). Assim como Galeano e Feijó (2012), o crédito bancário (CRED 0 e Δ CRED) também revelou-se importante, especialmente em locais com população entre 50-500 mil habitantes (Tabela 4).
5. CONCLUSÃO
A essência da economia, como ciência, consiste em gerenciar recursos escassos a fim de maximizar o bem-estar geral. Assim, assumindo-se que locais com populações semelhantes seriam mais homogêneos entre si e demandariam políticas próprias, esta pesquisa usou um painel-espacial, com dummies interativas (contendo dados de 5505 municípios brasileiros, entre as décadas de 2000-2010 e 2010-2020), para avaliar quais ações seriam mais adequadas ao crescimento econômico de localidades com diferentes portes populacionais.
Os resultados indicam que a efetividade das políticas econômicas diminui à medida que aumenta o porte populacional. Portanto, há mais espaço para intervenções nos municípios de menor porte. Além disso, cada localidade parece demandar ações específicas para mitigar os problemas da faixa populacional à qual pertence, o que inviabiliza o uso de políticas universais, válidas e efetivas para localidades marcadamente heterogêneas.
Dentre estas ações, nota-se que populações mais educadas favoreceriam o crescimento dos municípios com até 50 mil habitantes. Já a falta de saneamento básico, possivelmente por comprometer a saúde dos trabalhadores, seria nociva aos municípios de pequeno e médio porte. Em locais com até 500 mil habitantes, a concentração industrial e/ou no setor de serviços revelou-se benéfica. Por outro lado, depender excessivamente da administração pública constitui um entrave. A concentração de trabalhadores em poucos setores parece gerar ganhos de escala e de especialização, mostrando-se vantajosa aos municípios com até 100 mil habitantes. Já populações mais jovens - geralmente com menor experiência e maior rotatividade no emprego - inibem o crescimento dos locais com até 50 mil habitantes. Apesar do risco associado ao déficit fiscal, os gastos públicos de capital mostraram-se promissores para os municípios com até 50 mil habitantes, enquanto os gastos correntes estimulam o crescimento em todas as faixas populacionais. Ademais, o acesso ao crédito bancário revelou-se importante para os municípios com 50 a 500 mil habitantes. Nas cidades com até 25 mil habitantes, devido à baixa diversificação produtiva, a proximidade de vizinhos de maior porte pode acelerar o crescimento. Todavia, essa relação se inverte entre os municípios de 25 a 50 mil habitantes e perde significância nas faixas populacionais mais elevadas.
Ao indicar quais fatores associados ao crescimento econômico municipal seriam mais adequados a cada porte populacional, acredita-se que os resultados deste estudo possam contribuir para a elaboração de políticas econômicas mais eficazes, que considerem as heterogeneidades existentes entre municípios com diferentes faixas populacionais. Ainda assim, destaca-se que a escassez de variáveis socioe-conômicas na esfera municipal, previamente descritas por Firme e Simão Filho (2014, p.687-689), impõe uma séria limitação a esta pesquisa. Ademais, o uso de apenas dois períodos de analise (i.e.: 2000-2010 e 2010-2020) restringe a possibilidade de implementação de certos ajustes econométricos. No painel dinâmico, por exemplo, o controle da endogeneidade via difference GMM (Arelano e Bond, 1991) requer ""instrument the right-hand-side variables in the first-differenced equations using levels of lagged two periods or more" (Bond, Hoeffler e Temple, 2001, p.2-3). Portanto, recomenda-se que futuras pesquisas sejam conduzidas com métodos estatísticos alternativos, bem como diferentes recortes temporais e territoriais, a fim de reforçar ou refutar os resultados aqui obtidos.