Del análisis y la representación de situaciones espaciales hacia el pensamiento teórico en geometría: una ruta de tercero a noveno grado^*

From analysis and representation of space situations, to theoretical thinking in Geometry: A grade 3 - grade 9 pathway

Paolo Boero^**

^*Este artículo fue presentado a la revista en Inglés inicialmente, y fue traducido por Carmen Inés Samper y Patricia Perry, docentes de la Universidad Pedagógica Nacional.
^**Departamento de Matemáticas. Universidad de Génova (Italia). Genova, Italia. boero@pitagora.dima.unige.it

Recibido: 15/01/12, aprobado: 15/11/12

Resumen

A partir de ejemplos provenientes de un proyecto que inició a finales de los años 1970, y que ha sido ampliamente experimentado en la escuela primaria y los primeros cursos de secundaria, me propongo ilustrar cómo es posible moverse desde la construcción argumentativa de conceptos geométricos en campos de experiencia adecuados (en particular, en el campo de experiencia de las sombras solares) hacia el desarrollo de las competencias argumentativas necesarias para validar conjeturas en geometría y para aproximarse a teoremas de la geometría tridimensional. La producción y validación argumentativa de hipótesis relacionadas con ciertos fenómenos y situaciones espaciales proveen oportunidades a los estudiantes tanto para desarrollar la conceptualización en el campo de la geometría como para tener un acercamiento al razonamiento hipotético ("si... entonces..."), al encadenamiento deductivo de proposiciones, etcétera. La mayoría de los ejemplos tienen que ver con situaciones tridimensionales de sombras producidas por el sol.

Palabras Clave Geometría de las sombras solares, argumentación, conceptualización, aproximación a la prueba.

Abstract

The aim of this paper is to illustrate, through examples taken from a Project widely experimented in primary and lower secondary school since the end of the seventieths, how it is possible to move from the argumentative construction of geometrical concepts in suitable fields of experience (in particular, the field of experience of sun shadows) to the development of students' argumentative skills that are needed to validate conjectures in geometry, and to their approach to 3-D geometry theorems. Production and argumentative validation of hypotheses concerning suitable space situations and phenomena provide students with the opportunity of both developing conceptualization in the field of geometry, and approaching hypothetical reasoning ("if... then..."), deductive enchaining of propositions, etc. Most examples will deal with 3D-situations concerning sun shadows

Keywords Geometry of sun shadows; argumentation; conceptualization; approach to proof.

Introducción

Académicos, entre quienes cabe citar a Balacheff, Duval, Dreyfus, Harel y Hoyles, han realizado varias investigaciones, en particular en las dos últimas décadas del siglo pasado, con el propósito de identificar e interpretar las dificultades que enfrentan los estudiantes al aproximarse a la demostración y a los aspectos teóricos de las matemáticas. Varias causas se han considerado: desarrollo deficiente de las habilidades argumentativas, manejo insuficiente de los conceptos involucrados en los teoremas que se han de demostrar, falta de motivación para validar mediante razonamiento deductivo enunciados cuya veracidad es evidente, necesidad de pasar de la validación empírica a la teórica, y falta de comprensión de lo que significa demostrar en matemáticas (una visión panorámica se puede encontrar en Boero, Douek y Ferrari, 2008).

Desde comienzos de los años 1990, y bajo la perspectiva del paradigma italiano de "investigar para innovar", el Genoa Research Team, grupo de investigación en educación matemática, se involucró en actividades de investigación y desarrollo concernientes a la mejora de las habilidades argumentativas de los estudiantes de la escuela elemental (grados primero a quinto) y al acercamiento de los estudiantes a la actividad demostrativa y a los aspectos teóricos de las matemáticas, en los primeros años de la escuela secundaria (grados sexto a octavo) (véase Arzarello y Bartolini Bussi, 1998). El contexto de la investigación lo constituyeron los dos proyectos desarrollados desde finales de los años 1970 para la enseñanza integrada de las matemáticas y las ciencias en grados sexto a octavo, y para la enseñanza de las disciplinas más importantes (en particular, la lengua italiana y las matemáticas) en los grados primero a quinto. Contaron con dos circunstancias importantes: por una parte, al comienzo de la década de 1990, los proyectos desarrollados por el equipo ya estaban maduros y esto posibilitó ampliar las metas; por otra parte, un grupo de treinta profesores e investigadores universitarios habían aprendido a colaborar de manera eficaz en la elección de preguntas de investigación de interés común y en la planeación y análisis de experimentos de enseñanza. De manera gradual, se fueron conectando los dos propósitos -mejorar las habilidades argumentativas de los estudiantes en los primeros grados y aproximar a los estudiantes a la demostración y los aspectos teóricos en los grados sextos a octavo- entre sí y con el compromiso previo relativo al desarrollo del conocimiento matemático de los estudiantes. El hecho de que en ambos proyectos se persiguiera la construcción de conceptos mediante actividades de resolución de problemas contextualizadas en "campos de experiencia" (Boero et al., 1995; Dapueto y Parenti, 1999; Douek, 1999) relacionados con la vida cotidiana de los estudiantes, nos sugirió la posibilidad de abordar la demostración matemática en situaciones de modelación matemática (véase Boero y Garuti, 1994; Boero, Garuti, Lemut y Mariotti, 1996; Boero, Garuti y Lemut, 2007).

En este artículo se presentan (a través de algunas situaciones problema que representan pasos cruciales en la ruta de grados primero a octavo) cómo se desarrolla la argumentación en estricta conexión con la conceptualización y cómo resulta en habilidades y conocimiento que pueden permitir una aproximación suave para realizar actividades de conjeturación y demostración. Por lo regular, los profesores eligen y agregan otras situaciones problema para consolidar y ampliar los resultados de aprendizaje -espero que las instantáneas que presento aquí le permitan al lector capturar algunas características relevantes de la ruta-.

La ruta que se reporta aquí es resultado de una tarea colectiva de profesores e investigadores, que tomó varios años; algunos de sus nombres se indican como autores en los artículos citados, pero muchos otros, no mencionados, contribuyeron en la elaboración de ideas y en actividades experimentales.

Este texto no trata directamente con posiciones teóricas y constructos que subyacen en la planeación, el manejo y el análisis de situaciones didácticas; sin embargo, en algunos puntos se indican de manera breve algunos elementos teóricos o se alude a ellos. Para obtener referencias más precisas relativas al marco teórico, véase: Bishop (1988) (en lo que tiene que ver con las bases antropológicas e históricas); Boero (1989), Boeroet al. (1995), Dapueto y Parenti (1999), Douek (2003), Boero y Douek (2008) (en lo que concierne al desarrollo del conocimiento matemático de los estudiantes "en contextos cotidianos" -por ejemplo, campos de experiencia- y a las elecciones didácticas relacionadas); Dapueto y Parenti (1999) (en lo relacionado con la modelación matemáticas); Douek (1999) y Douek y Scali (2000) (en lo relativo a la argumentación y la conceptualización); Boero, Douek y Ferrari (2008) (en lo relativo a asuntos lingüísticos y relaciones entre argumentación y demostración); Boero, Garuti, Lemut y Mariotti (1996), Garuti, Boero y Lemut (1998) y Pedemonte (2005, 2007) (en cuanto a la unidad cognitiva de teoremas y desarrollos investigativos posteriores); Boero, Douek, Morselli y Pedemonte (2010) (en lo relacionado con el encuadramiento teórico de la aproximación de los estudiantes a la "cultura de los teoremas" y la integración del comportamiento racional, constructo de Habermas, con la teoría de la argumentación de Toulmin).

Concepciones de los estudiantes y modelación geométrica de sombras solares (grados tercero y cuarto)

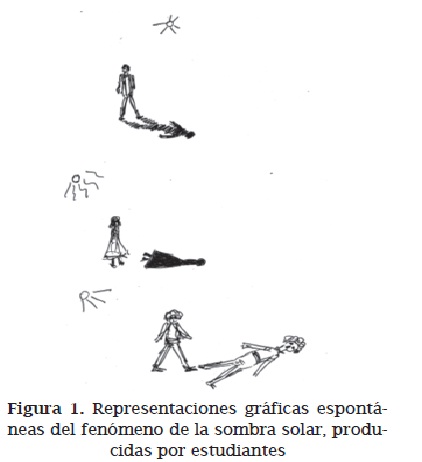
La mayoría de los dibujos de sombras solares que producen los estudiantes (en grado tercero, pero también en grado sexto) parecen derivarse de una concepción no geométrica del fenómeno de la sombra solar. En el caso de la sombra del cuerpo humano, la variedad de dibujos es muy extensa:

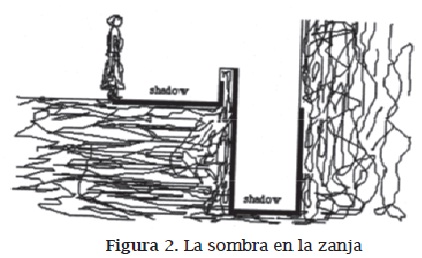
Aun después de una actividad de larga duración en torno al modelo geométrico de sombras solares, continúan surgiendo algunas concepciones de índole no geométrica (las muy relacionadas con la percepción: concepción de alfombra y reflexión) cuando se propone una tarea exigente y compleja como la siguiente (Boero et al., 1995):

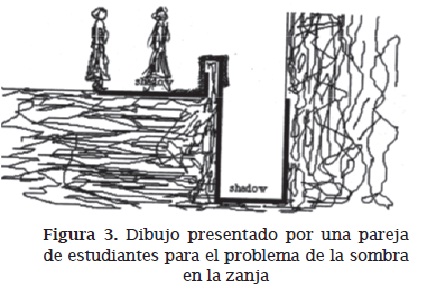
El dibujo representa una vista lateral de una situación de sombras producidas por el sol. Una persona se está acercando a la pared bajita y se representa su sombra. Del otro lado de la pared bajita, hay una zanja profunda y en seguida una pared alta. El dibujo muestra el área de la zanja que se mantiene en la sombra. Tarea: Dibuje la persona representada en el dibujo y el lugar donde estará su sombra si ella se mueve hacia adelante unos tres pasos".

Algunos adultos (incluso algunos profesores de ciencia) producen dibujos parecidos.

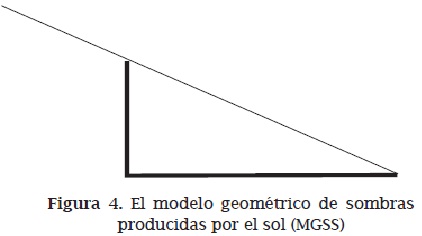
En la historia y la epistemología de la ciencia, el modelo geométrico de sombras solares (MGSS) se considera la primera entidad geométrica que no se deriva de la abstracción de algo concreto, de cosas visibles (Serres, 1993). Realmente no podemos ver el rayo de sol que conecta el sol, la parte superior del objeto y el extremo de la sombra producida.

Tratar con el MGSS no es tarea fácil para los profesores, si quieren que los estudiantes se acerquen a dicho mode-lo de forma constructiva. Es necesario guiar a los estudiantes a través de observaciones y situaciones problema adecuadas (véase Scali, 1999 -para una presentación comprensiva de este tema- y Boero, 2002). Como resultado, los estudiantes pueden aprender mucha geometría, además del modelo mismo.

Se presentan a continuación dos ejemplos de situaciones problema para grado tercero, que tienen un doble propósito; por un lado, preparar las bases para la introducción del GMSS y, por otro, desarrollar competencias geométricas y argumentativas.

El juego del sol y la sombra

Un estudiante camina alrededor del patio del colegio con una banda sobre sus ojos; debe decir cuándo está en la sombra y cuándo en la parte soleada. Los demás estudiantes se dan cuenta de que la sombra en el piso corresponde a un espacio de sombra (de hecho, es la sección del cilindro sombra con el piso). Comienzan a notar que existen algunas relaciones de "paralelismo", en el espacio, entre las líneas que conectan la parte superior de los objetos, que producen las sombras, y los extremos de las sombras.

¿Cómo medir su propia sombra?

Esta situación problema refuerza la intuición que se tiene sobre la línea recta que conecta la cabeza del estudiante y el extremo de su sombra, y saca a relucir (de acuerdo con las estrategias adoptadas por los estudiantes) algunas propiedades importantes de la medida de longitudes (como su invariancia por traslación o su aditividad). Más aún, cuando los estudiantes comparan sus estrategias y discuten sobre ellas, guiados por el profesor, necesitan for-mas argumentativas importantes para explicar "por qué esa estrategia no funciona" o "por qué es lo mismo hacer esto o lo otro".

"La estrategia de Michela puede no funcionar si ella no encuentra señales apropiadas en el piso para sus pies y el extremo de su sombra; cuando se mueve para medir su sombra no tiene longitud por medir".

En cuanto al desarrollo de competencias argumentativas, parece que el MGSS modifica tanto las formas de pensar sobre la relación entre la altura del sol y la longitud de las sombras producidas, como las formas de expresar tal relación (véase Boero, 2002):

Muchos estudiantes de grados tercero y cuarto, que en su primer "informe de observación" escribieron: "en la mañana el sol está bajito en el horizonte y las sombras son largas", tras experimentar el MGSS, usaron expresiones diferentes: "en la mañana las sombras son largas porque el sol está bajito en el horizonte", e incluso, "si el sol está bajito en el horizonte, las sombras son largas".

Como ya se mencionó, la construcción del MGSS no es fácil para los estudiantes: requiere una fuerte mediación de parte del profesor. El peligro está en que el profesor imponga ese modelo como la única verdad y descalifique las concepciones y representaciones de los estudiantes. En realidad, un asunto importante para nosotros concierne al valor cultural de algunas concepciones no geométricas de las sombras solares: es cierto que para la mayoría de nuestros niños (italianos, pero también españoles o húngaros), algunas concepciones (particularmente aquellas que persisten en la adultez) parecen tener como causa la espontánea y personal adaptación piagetiana a estímulos visuales. Otras concepciones que no persisten en la adultez parecen reflejar ideas religiosas (el alma). Pero en otros países (en Eritrea, de acuerdo con nuestras observaciones directas, y también en la China, según estudios antropológicos (véase Cheng, 1997) se pueden detectar importantes concepciones no geométricas que están relacionadas con formas más generales de pensar los fenómenos naturales.

En los casos descritos, la imposición brusca del modelo geométrico puede constituir una pérdida cultural importante (¡aún en una perspectiva occidental, científica!). Por ejemplo, consideremos la concepción de sombras solares como un equilibrio dinámico y cíclico entre la luz y la oscuridad, que hemos identificado en Eritrea (concepción de la mayoría de los estudiantes de Eritrea del colegio italiano en Asmara) y que parece persistir en China. Se suma que en la cultura dialéctica-holística china, luz y oscuridad no pueden concebirse de manera separada (uno existe gracias al otro). ¡Esta forma de pensar las sombras solares cuadra perfectamente con el dinámico y cíclico equilibrio entre depredador y presa, y las limitaciones mutuas para la existencia de poblaciones de depredadores y de presas -usualmente un asunto ¡difícil para nuestra matemática occidental y para estudiantes universitarios de ciencias!-. También tendrían que considerarse otros fenómenos complejos en ecología, ciencias naturales y economía en la misma perspectiva dialécticaholística, tan rara para nuestras formas occidentales analíticas de pensamiento científico.

Modelo geométrico de sombras solares y construcción de conceptos geométricos mediante la argumentación (grados cuarto a sexto)

Este es el aspecto central de la ruta que permitirá que los estudiantes aborden tareas teóricas exigentes de geometría.

Una vez que los estudiantes se familiarizan con el MGSS, es hora de realizar observaciones gradualmente más precisas y tratar con problemas cada vez más complejos.

Construcción de la herramienta para observar

Una situación problema muy enriquecedora es:

"¿Cómo colocar una mesa de madera y una puntilla larga, para estudiar el comportamiento de sus sombras durante el día y en diferentes días durante el año?".

En el patio del colegio, tratando de encontrar posiciones convenientes para la mesa y la puntilla, los estudiantes experimentan la necesidad de darle una posición convencional tanto a la mesa como a la puntilla. Mediante el debate "en situación", guiado por el profesor, se llega a la solución de poner la mesa "horizontal", "en posición común" y a la puntilla "parada en posición derecha". Pero, ¿cómo lograr esas posiciones? Algunos estudiantes evocan el nivel usado por los adultos para comprobar la posición horizontal de una nevera o lavadora (experiencias familiares para ellos). Para encontrar la posición vertical de la puntilla, otros estudiantes sugieren otra experiencia familiar -una pita con una pesa-.

Los informes individuales escritos de los estudiantes sobre las actividades y las discusiones en el patio contienen mucha argumentación: "Hemos visto que si movíamos la puntilla, la longitud de la sombra cambiaba; por tanto teníamos que encontrar una posición que pudiera mantenerse igual durante todo el tiempo". Además, lleva muchos gérmenes de conceptos (conceptos-enacción) (Vergnaud, 1990) y relaciones geométricos:

"No era suficiente mantener la mesa horizontal en una dirección; era necesario comprobar la posición horizontal según dos direcciones diferentes".

En seguida, la tarea del profesor consiste en seleccionar unos pocos textos representativos y "ricos" de los estudiantes para dar una copia de éstos a cada estudiante y organizar una discusión grupal en torno a ellos.

La discusión debe ser guiada por el profesor, quien debe poner en evidencia, en los momentos oportunos, los conceptos y relaciones geométricos; por ejemplo:

"Se necesitan dos rectas horizontales orientadas de forma distinta (es decir, no paralelas) en la mesa para asegurar que la mesa esté horizontal."

Una síntesis individual escrita sobre "qué hemos aprendido durante la discusión" debe permitir al profesor evaluar los resultados de la actividad y promover más discusión grupal para reorientar, consolidar o favorecer la conceptualización de los estudiantes (según las necesidades individuales).

Podemos destacar la organización cíclica típica de la actividad (para más detalles, véase Boero y Douek, 2008), a partir de las experiencias de los estudiantes, ya sean estas de su vida extraescolar, o previamente organizadas por el profesor:

• Producción individual de textos escritos (con el apoyo individual del profesor para los aprendices lentos).
• Discusión grupal, guiada por el profesor en su papel de mediador (Bartolini Bussi, 1996), de unos pocos textos representativos, seleccionados por el profesor.
• Síntesis individuales escritas de las discusiones.
• Discusión grupal, guiada por el profesor en su papel de mediador, de algunas de las síntesis de los estudiantes.
• Síntesis final registrada por los estudiantes en sus cuadernos (como una conclusión temporal del ciclo de actividades), como un punto de inicio para posteriores desarrollos en ciclos posteriores.

La escala de reducción del abanico de sombra

Una vez instrumentalizado (Rabardel, 1995, 1999) el sistema mesa/puntilla (que, por ejemplo, se haya convertido en una herramienta científica clara en sus principios y que puede usarse con un propósito) se puede proponer otra situación problema importante: "¿Cómo dibujar el abanico de sombra grande que se ve en la mesa del patio, de manera que quepa en una hoja del cuaderno?".

El profesor escoge algunas de las respuestas de los estudiantes, posteriormente, éstas se discuten en clase.

En cuanto a los resultados conceptuales esperados, éstos son: la reducción de escalas bidimensionales (los estudiantes ya habían trabajado la reducción de escalas unidimensionales con sus alturas y las alturas de plantas cultivadas en clase), y la invariancia del ángulo por la reducción de sus lados.

La argumentación de los estudiantes respecto al problema del dibujo a escala del abanico de sombra es usualmente muy rica, tanto en formas de argumentación como en términos de contenido conceptual: "Debo dividir todas las longitudes de las sombras por cuatro, porque si divido las longitudes más cortas por dos la forma del abanico cambia".

Debo mantener igual la abertura del ángulo, porque si la reduzco por cuatro (como lo hice con las longitudes de las sombras) no respeto el movimiento de las sombras durante el día: al mediodía la dirección de la sombra no sería sur-norte, como lo es en la realidad".

Nótese cómo la referencia a la realidad guía la escogencia del criterio para la construcción, especialmente en el segundo caso. La geometría funciona como "una representación espacial", de acuerdo con lo que exigen los programas italianos de 1985 para la escuela primaria.

A continuación se presentan tres situaciones que tienen que ver con las representaciones mental y gráfica del fenómeno de las sombras.

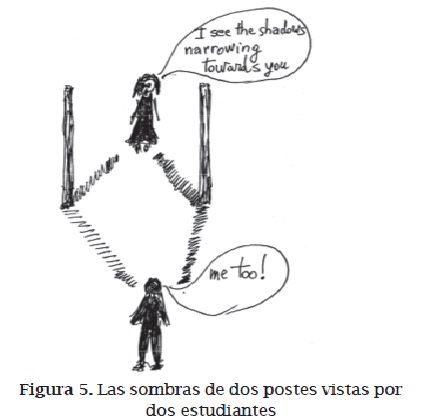
Las sombras de dos postes

Dos niños están parados en posiciones opuestas con respecto a dos postes altos. Ellos describen en voz alta lo que ven; ambos dicen: "Veo las sombras de los postes, que convergen hacia usted". Esta contradicción destaca la relación real entre las sombras en el piso ("como los rieles de tren", "paralelos", con "igual distancia entre ellos"), y el hecho de que, en la mayoría de los casos, las rectas paralelas se ven como rectas que convergen.

La mesa en otro patio

Al ejercicio "Si ponemos la mesa con la puntilla en el patio del preescolar que queda cerca, ¿qué le sucede a la longitud de la sombra a la misma hora del mismo día?" se producen diferentes soluciones:

• La misma longitud, porque el día y la hora son las mismas.
• La misma longitud, porque el sol ilumina la mesa de la misma forma (nótese que el paralelismo de los rayos provenientes del sol no intervienen) (figura 6).

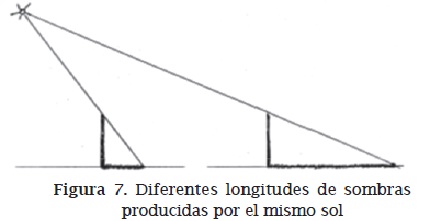
• Diferentes longitudes (figura 7)

Por medio de la comparación y la discusión de las hipótesis, se relaciona el paralelismo de los rayos solares con la distancia real del Sol a la Tierra. Es importante anotar que, por lo regular, la discusión que conduce a la solución correcta no inicia a partir del análisis de la respuesta "la misma longitud" relacionada con la figura 6, sino del análisis de la respuesta incorrecta respaldada por la figura 7. Esta es una ocasión importante para que los estudiantes experimenten cómo una hipótesis incorrecta puede llevar a desarrollos productivos, mientras que una respuesta correcta puede descansar en justificaciones que no conducen a nada distinto.

La altura del sol

Una última tarea, muy exigente para la argumentación (y la conceptualización relacionada) (véase Douek, 1999) es:

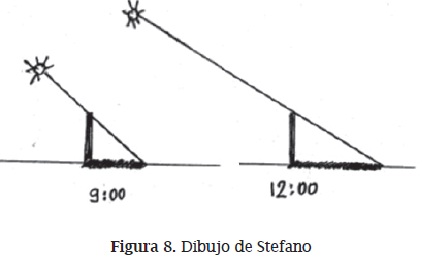
"Al comienzo del trabajo en clase sobre sombras solares, Stefano (un estudiante de grado sexto) cree que las sombras son más largas cuando el sol está más alto y fuerte. Otros estudiantes creen lo contrario. Para explicar su hipótesis, Stefano produce el siguiente

"Y escribe: ‘Como podemos ver en el dibujo, el sol produce una sombra más larga cuando está más alto, eso es al mediodía, cuando también es más fuerte'.

Sabemos muy bien que las sombras son más largas cuando el sol está más bajo (temprano en la mañana y tarde en la tarde). Por tanto, en el razonamiento de Stefano hay algo que no funciona. ¿Qué está mal en el razonamiento de Stefano y, particularmente, en su dibujo? Trate de explicarse claramente para que Stefano pueda entender".

La argumentación debe cumplir el papel de aclarar la distinción entre la altura como una distancia medible y la altura angular en el espacio; durante la discusión de los textos individuales de los estudiantes (seleccionados, como siempre, por el profesor) aparecen otros conceptos geométricos y habilidades importantes:

• Paralelismo y perpendicularidad.
• La posición ficticia, evocativa del sol en el dibujo.
• El ángulo como la inclinación de una línea recta con respecto a otra (definición de Euclides).

La complejidad de la argumentación (en términos de la tríada data/conclusión/garantía de Toulmin, 1958/1974) refleja la complejidad de la situación problema:

"Stefano no tiene razón porque en el dibujo no se representa la posición real del sol; basta dibujar al sol en otra posición del rayo solar y la altura del sol cambia; por tanto, la distancia desde el piso no es lo importante".

Argumentación respecto a las sombras solares y la aproximación a conjeturar y demostrar (grados séptimo y octavo)

Imagínese que los estudiantes de grado séptimo hayan seguido la ruta sugerida para los grados tercero a sexto, algunos de cuyos pasos se han descrito anteriormente (o que han seguido una ruta similar condensada en la que han invertido entre 80 y 100 horas en grado sexto); están listos para aproximarse a la conjeturación y la demostración para situaciones espaciales en grados séptimo y octavo, porque:

• Manejan conceptos geométricos cruciales del espacio.
• Han desarrollado habilidad es argumentativas en términos de suficiente "complejidad, según Toulmin", y de una variedad de formas de argumentación (el constructo "si... entonces...", "las implicaciones...","por tan-to..."y "... porque..., la oposición... "mientras que...").
• Están acostumbrados al patrón cíclico del trabajo en clase, descrito anteriormente.

¿Por qué situaciones espaciales?

Muchas situaciones geométricas 2D son adecuadas para la conjeturación, pero en general las más sencillas (aquellas accesibles para estudiantes primíparos en la demostración) son visualmente triviales

o fáciles de demostrar, tomando medidas de la figura. ¡No hay necesidad intelectual para demostrar mediante el razonamiento general! Además, la producción de conjeturas no necesita elaboración sustancial -es suficiente mirar algunos dibujos-.

Algunas situaciones espaciales proveen a los estudiantes dos tipos de oportunidades:

• Para conjeturar es necesario imaginar y ver desde diferentes puntos de vista y, por tanto, es una elaboración compleja; los argumentos producidos durante la fase de conjeturación (de la plausibilidad de la conjetura, los estudiantes están acostumbrados a producir soluciones motivadas) pueden reorganizarse bajo la guía del profesor, para obtener una demostración (unidad cognitiva de teoremas). (Véase Garuti, Boero y Lemut, 1998; Pedemonte, 2005; 2007; 2008).
• Las conjeturas no son visualmente triviales, y no es posible demostrar por medidas en las situaciones 3D; por tanto, se motiva la demostración por razonamiento general como única forma de asegurar la verdad de la conjetura.

La situación problema de los dos palos

Según nuestras experiencias, la mejor situación espacial para aproximarse a la conjeturación y la demostración en grado octavo es la siguiente; ha sido replicada en varios cursos, siempre con éxito (se necesitan de diez a doce horas de trabajo en clase):

1. Proponer el problema y producir conjeturas escritas de manera individual:
2. "En años pasados, observamos que las sombras de dos palos verticales en el piso horizontal siempre son paralelas. ¿Qué puede decirse del paralelismo en el caso de un palo vertical y uno oblicuo? ¿Pueden ser paralelas las sombras? ¿En ocasiones? ¿Cuándo? ¿Siempre? ¿Nunca? Justifique su respuesta".
(No hay rayos solares en el aula pero están disponibles unos palos largos y delgados y tres o cuatro plataformas de icopor).
3. Discutir conjeturas: se discuten, con la ayuda del profesor, algunas conjeturas seleccionadas, hasta obtener colectivamente afirmaciones de conjeturas correctas, que reflejen las diferentes aproximaciones de los estudiantes al problema.
4. Organizar las afirmaciones: a través de diferentes discusiones, guiados por el profesor, pueden obtenerse colectivamente los siguientes tipos de afirmaciones limpias de metáforas y más precisas, desde un punto de vista lingüístico, que aquellas producidas inicialmente por los estudiantes:

• "Si los rayos del sol pertenecen al plano vertical del palo oblicuo, las sombras son paralelas".
• "Si el palo oblicuo se mueve en un plano vertical que contiene a los rayos del sol, entonces las sombras son paralelas".
• "Las sombras de los dos palos serán paralelas solo si el plano vertical del palo oblicuo contiene rayos del sol".

Las dos primeras afirmaciones muestran dos formas diferentes de acercarse al problema por parte de los alumnos: el movimiento del sol y el movimiento de los palos; la tercera afirmación hace explícita la unicidad de la situación en la que las sombras son paralelas. Después de más discusión, debe obtenerse la construcción colectiva de las siguientes afirmaciones:

"Si los rayos del sol pertenecen al plano vertical del palo oblicuo, las sombras son paralelas. Las sombras son paralelas solo si los rayos del sol pertenecen al plano vertical del palo oblicuo".

"Si el palo oblicuo está en un plano vertical que contiene los rayos del sol, las sombras son paralelas. Las sombras son paralelas solo si el palo oblicuo está en un plano vertical que contiene los rayos del sol".

d. Preparar la demostración: se llevan a cabo las siguientes actividades:

• Búsqueda individual de semejanzas y diferencias entre la conjetura inicial propia y las tres afirmaciones limpias consideradas durante la etapa
• Tarea individual: "¿Qué cree acerca de la posibilidad de comprobar nuestras conjeturas con un experimento?".
• Discusión de las respuestas de los estudiantes a la pregunta previa.

Durante la discusión, los estudiantes deben darse cuenta gradualmente de que una comprobación experimental es "muy difícil" porque uno debe examinar lo que sucede "en todas las infinitas posiciones del sol y en todas las infinitas posiciones de los palos".

Esta etapa larga de la actividad (alrededor de tres horas) se planea para propiciar que los estudiantes, de manera crítica, tomen distancia con respecto a las afirmaciones, motivarlos a demostrar, y aclarar que desde ese momento el trabajo de la clase tiene que ver con la validez de la afirmación "en general".

e. Demostrar la parte "si" de la afirmación (por ejemplo, la condición es suficiente).

f. Demostrar la parte "solo si" de la afirmación (por ejemplo, la condición es necesaria).

g. Hacer una discusión final, seguida por un informe individual sobre la actividad completa (en la clase, se necesitan alrededor de dos horas; o en la casa).

Comentarios acerca del potencial del software de geometría dinámica para conjeturar y demostrar

Aceptar que las situaciones espaciales son adecuadas para aproximarse de manera suave a las actividades de conjeturar y demostrar no significa desconocer el debate actual del potencial del software de geometría dinámica (SGD) para el mismo propósito (Mariotti et al., 1997). Creo que sería necesario proveer evidencia experimental para las siguientes hipótesis:

• Las situaciones en dos dimensiones que se pueden trabajar con el apoyo del software son mejores que las situaciones espaciales en lo que concierne a la creación de la necesidad intelectual de demostrar.
• A pesar de la facilidad de explorar situaciones de dos dimensiones, los SGD no inhiben la imaginación (por ejemplo, exploración virtual con los ojos de la mente).

Según mi conocimiento, tal evidencia aún hace falta.

Pero alguien podría decir: "situaciones espaciales como la de los dos palos son seguramente eficientes para el acercamiento a actividades de conjeturar y demostrar; sin embargo, se deben preparar a través de actividades de largo plazo con otras situaciones espaciales [...]".

Mi respuesta sería: "Cierto, pero esas situaciones espaciales también propician las competencias argumentativas de los estudiantes y promueven su dominio de conceptos geométricos importantes del espacio, una meta importante para la educación geométrica de ahora".

Geometría de sombras solares, geometría de representaciones 2D del espacio visual: el acercamiento a la cultura de teoremas (grados octavo y noveno)

Con la expresión cultura de teoremas, implicamos la capacidad de conjeturar y demostrar junto con notar los aspectos sobresalientes de un teorema como una tríada (Mariotti et al., 1997): el enunciado, la teoría de referencia y la demostración de un enunciado, realizada dentro de la teoría de referencia (enunciados de referencia y reglas de inferencia).

En nuestro grupo de investigación tenemos un interés especial en una aproximación temprana a la cultura de teoremas; en este momento, Nadia Douek y Francesca Morselli están particularmente comprometidas con elaboraciones teóricas y actividades experimentales sobre el desarrollo de la conciencia lograda por los estudiantes, en cuanto a la organización general de una demostración dentro de una teoría (en grados octavo y noveno: véase Boero, Douek, Morselli y Pedemonte, 2010). Hace unos años, Laura Parenti y un grupo de tres profesores replicaron en nueve cursos de grado octavo un experimento de enseñanza cuyo propósito era que los estudiantes adquirieran la conciencia del hecho de que la verdad de una afirmación depende de los presupuestos considerados como verdaderos en un sistema de referencia. Presentaré acá un esquema del trabajo liderado por Parenti (2007).

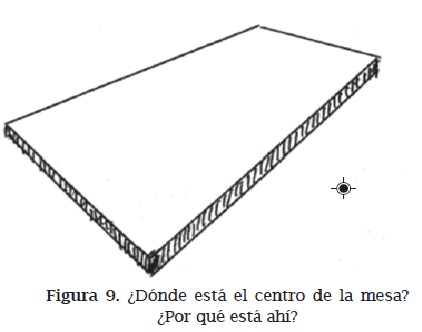
Los alumnos de los nueve cursos experimentales habían seguido, en los grados sexto a octavo, la ruta de sombras solares descrita anteriormente (incluyendo el problema de los dos palos); también habían trabajado algunos problemas relacionados con representaciones 2D de situaciones espaciales visuales, en particular, cómo encontrar el centro de una mesa rectangular representada en perspectiva -una situación problema experimentada en clases de primaria por el grupo de investigación dirigido por Mariolina Bartolini Bussi (1996)-.

En ambos casos, los estudiantes pasaron de un campo de experiencia familiar (por ejemplo, sombras solares) a la geometría de ese campo de experiencia y a algunas de sus propiedades evidentes. Por ejemplo, en el caso de la geometría de sombras solares (la geometría de las sombras producidas por el sol en una superficie plana):

• Líneas rectas producidas por el sol se transforman en líneas rectas o puntos de la superficie del plano.
• Líneas rectas paralelas producidas por el sol se transforman en líneas rectas paralelas (o que coinciden) o puntos en la superficie del plano.

En ambos casos, los estudiantes aprendieron a inferir afirmaciones a partir de las propiedades que parecían obvias para ellos y a moverse progresivamente hacia el formato usual de las demostraciones.

Al final del experimento de enseñanza, en grado octavo, los estudiantes se dieron cuenta de que la afirmación "Un rectángulo se puede transformar en un paralelogramo o segmento" se puede validar en la geometría de las sombras solares, pero, en cambio, la misma afirmación no es generalmente cierta en la geometría de la representación de situaciones espaciales visuales. También descubrieron que la demostración en la geometría de las sombras solares se basa en una propiedad obvia (rectas paralelas no se transforman necesariamente en rectas paralelas), pero, en cambio, esta propiedad no es aceptable como una "propiedad obvia" en la geometría de la representación de situaciones espaciales visuales porque las rectas paralelas no se transforman necesariamente en rectas paralelas. De esta forma, los estudiantes aprendieron que las situaciones espaciales pueden considerarse desde más de un punto de vista: el de un observador y el del sol, que se considera está a una distancia infinita, lo que resulta en propiedades obvias diferentes y en distintas conclusiones obtenidas válidamente.

En resumen, considerar sistemas de postulados como propiedades obvias de representaciones espaciales, de acuerdo con las formas específicas de pensarlas, no solo recuerda el origen del descubrimiento de las geometrías no-euclidianas (en particular, Lobachevski) sino también coincide con algunas posiciones epistemológicas recientes concernientes a las conexiones cercanas entre axiomáticas geométricas y formas relacionadas de ver y pensar sobre el espacio (véase Berthoz, 1998 o Longo, 2009).

Comentarios finales

A menudo, cuando presentamos la ruta nos preguntan: "¿por qué involucrar tan tempranamente (antes de finalizar la educación obligatoria, en Italia y Francia) a profesores y estudiantes en la cultura de los teoremas?". Vemos dos razones importantes para ello:

Una, como reacción a la "escuela global de competencias" consideradas como piezas técnicas de un desarrollo intelectual subalterno, sin una perspectiva cultural amplia, y en consecuencia, incapaces de dar como resultado una personalidad autónoma. Y tanto estudiantes como profesores se mantienen alejados de sus raíces históricas (Bishop, 1988), sus cimientos epistemológicos y el significado del conocimiento matemático en culturas contemporáneas.

Otra, como una posibilidad de desarrollar en profesores (en la perspectiva de escuelas venideras) y estudiantes el conocimiento y la conciencia de una "racionalidad" (Habermas, 1999; véase Boero, Douek, Morselli y Pedemonte, 2010 para una adaptación del caso de la demostración,) que es una de las piedras angulares de la cultura científica occidental, para que puedan reconocerla y compararla con otras "racionalidades" pasadas y contemporáneas concebidas para satisfacer diferentes necesidades.

Referencias

Arzarello, F. y Bartolini Bussi, M. (1998). Italian trends in research in mathematics education: A national case study in the international perspective. En: A. Sierpinska y J. Kilpatrick (eds.) (1997). Mathematics education as a research domain: A search for identity (vol. 2, pp. 243-262). Boston: Kluwer Academic Publishers.         [ Links ]

Bartolini Bussi, M.G. (1996). Mathematical discussion and perspective drawing in primary school. Educational Studies in Mathematics, 31(1-2), 11-41.         [ Links ]

Berthoz, A. (1998). Le sens du mouvement. París: Ed. Odile Jacob.         [ Links ]

Bishop, A. (1988). Mathematical enculturation. Dordrecht: Kluwer Academic Publishers.         [ Links ]

Boero, P. (1989). Mathematics literacy for all. En Proceedings of PME-XIII (vol. 1, pp. 62-76 ). París.         [ Links ]

Boero, P. (2002). Geometric signs and students' verbal reports: The case of the geometric model of sunshadows. En Proceedings of PME-XXVI (vol. 2, pp. 129-136). Norwich: PME.         [ Links ]

Boero, P.; Dapueto, C.; Ferrari, P.; Ferrero, E.; Garuti, R.; Lemut, E.; Parenti, L. y Scali, E. (1995). Aspects of the mathematics-culture relationship in mathematics teaching-learning in compulsory school. Proceedings of PME-XIX, (vol. 1, pp. 151-166). Recife: PME.         [ Links ]

Boero, P. y Douek, N. (2008). La didactique des domainesd'expérience. Carrefours de l'Education, 26, 103-119.         [ Links ]

Boero, P.; Douek, N.; Morselli F. y Pedemonte, B.(2010). Argumentation and proof: A contribution to theoretical perspectives and their classroom implementation. En Proceedings of PME-XXXIV (vol. 1, pp. 179-205). Belo Horizonte: PME.         [ Links ]

Boero, P.; Douek, N. y Ferrari, P.L. (2008). Developing mastery of natural language: approach to theoretical aspects of mathematics. En: L. English (ed.). Handbook of international research in mathematics education (pp. 262-295). Nueva York y Londres: Routledge.         [ Links ]

Boero, P. y Garuti, R. (1994). Approaching rational geometry: From physical relationships to conditional statements. En Proceedings of PME-XVIII (vol. 2, pp. 96-103). Lisboa: PME.         [ Links ]

Boero, P.; Garuti, R. y Lemut, E.(2007). Approaching theorems in grade VIII: Some mental processes underlying producing and proving conjectures, and conditions suitable to enhance them. En: P. Boero (ed.), Theorems in school: From history, epistemology and cognition to classroom practice (pp. 249-264). Rotterdam, The Netherlands: Sense Publishers.         [ Links ]

Boero, P.; Garuti, R.; Lemut, E. y Mariotti, M.A. (1996). Challenging the traditional school approach to theorems: A hypothesis about the cognitive unity of theorems. En Proceedings of PMEXX (vol. 2, pp. 113-120). Valencia: Universidad de Valencia- PME.         [ Links ]

Boero, P.; Garuti, R.; Lemut, E., Gazzolo, T. y Llado', C. (1995). Some aspects of the construction of the geometrical conception of the phenomenon of sunshadows. En Proceedings of PMEXIX (vol. 3, pp. 3-10). Recife: PME .         [ Links ]

Cheng, A. (1997). Histoire de la penséechinoise. París: Editions du Seuil.         [ Links ]

Dapueto, C. y Parenti, L. (1999). Contributions and obstacles of contexts in the development of mathematical knowledge. Educational Studies in Mathematics, 39, 1-21.         [ Links ]

Douek, N. (1999). Argumentation and conceptualisation in context. Educational Studies in Mathematics, 39, 89-110.         [ Links ]

Douek, N. y Scali, E. (2000). About argumentation and conceptualisation. En Proceedings of PME-XXIV (vol. 2, pp. 249-256). Hiroshima.         [ Links ]

Garuti, R., Boero, P. y Lemut, E. (1998). Cognitive unity of theorems and difficulty of proof. En Proceedings of PME-XXII (vol.2, 345-352). Stellenbosch: PME.         [ Links ]

Habermas, J. (1999). Warheit und Rechtfertigung. Frankfurt: SuhrkampVerlag.         [ Links ]

Longo, G. (2009). Theorems as constructive visions.En Proceedings of the ICMI-Study 19 (vol. 1, pp. 13-25). Taipei: ICMI.         [ Links ]

Mariotti, M.A.; BartoliniBussi, M.; Boero, P.; Ferri, F. y Garuti, R.(1997). Approaching geometry theorems in contexts. En Proceedings of PME-XXI (vol. 1, pp. 180-195). Lahti (FI): PME.         [ Links ]

Parenti, L.; Barberis, M.T.; Pastorino, M. y Viglienzone, P. (2007). From dynamic exploration to "theory" and "theorems" (from 6th to 8th grades). En P. Boero (Ed.), Theorems in school: From history, epistemology and cognition to classroom practice (pp. 265-284). Rotterdam, The Netherlands: Sense Publishers.         [ Links ]

Pedemonte, B. (2007). How can the relationship between argumentation and proof be analysed? Educational studies in mathematics, 66, 23-41.         [ Links ]

Pedemonte B. (2005). Le modèle de Toulmin: unoutil pour l'analyse de l'unité cognitive. Recherches en didactique des mathématiques, 25(3), 313-348.         [ Links ]

Rabardel, P. (1995). Les hommeset les technologies, approche cognitive des instruments contemporains.París: Armand Colin.         [ Links ]

Rabardel P. (1999) Eléments pour une approche instrumentale en didactique des mathématiques. En Actes de la XIème Ecole de Didactique des Mathématiques, (vol. 1, pp. 203-213). Houlgate.         [ Links ]

Scali, E. (1999). Choix des tachesetorganisation des intéractionsdans la classepourl'appropriation des signes de la géométriedans les activités de modélisation. En Actes de la CIEAEM-49 (pp. 87-94). Setubal.         [ Links ]

Serres, M. (1993). Les origines de la géométrie. París: Flammarion.         [ Links ]

Toulmin, S. (1974). The uses of argument. Cambridge: Cambridge University Press.         [ Links ]

Vergnaud, G. (1990). La théorie des champs conceptuels. Recherches en Didactique des Mathématiques, 10, 133-170.         [ Links ]