Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Cuadernos de Economía
Print version ISSN 0121-4772On-line version ISSN 2248-4337
Cuad. Econ. vol.27 no.48 Bogotá Jan./June 2008
LA CURVA DE RENDIMIENTOS: UNA REVISIÓN METODOLÓGICA Y NUEVAS APROXIMACIONES DE ESTIMACIÓN
Juan Camilo Santana*
* Magíster en Estadística y Jefe de Riesgo de Mercado en Stanford Bolsa & Banca- Comisionista de Bolsa S.A. (Bogotá, Colombia). E-mail: camilosant@gmail.com . Este artículo fue recibido el 20 de diciembre de 2006 y su publicación aprobada el 15 de abril de 2008.
Resumen
La curva de rendimientos es una herramienta utilizada ampliamente, por quienes toman las decisiones de política monetaria o planifican sus inversiones, de acuerdo con la valoración, negociación o cobertura sobre instrumentos financieros. Debido a su importancia, el interés del artículo es evaluar el desempeño de un conjunto de modelos econométricos en el ajuste de la estructura a plazos de las tasas de interés (en el escenario del mercado de deuda pública en Colombia y en Estados Unidos), y en las distintas formas que pueden tomar las curvas de rendimientos. Los resultados revelan las bondades en el ajuste de las redes neuronales artificiales (RNA), la curva de Svensson, la curva de Nelson-Siegel y los polinomios locales. No obstante, se recomienda utilizar la curva de Svensson en la estimación de las tasas de interés, debido a la interpretabilidad de sus parámetros y a su superioridad sobre la Curva de Nelson-Siegel.
Palabras clave: curva de rendimientos, Nelson-Siegel, Svensson, regresión Kernel, splines suavizados, polinomios locales, supersuavizador de Friedmann, polinomios trigonométricos, redes neuronales. JEL: C29, C51, C45, C53
Abstract
The yield curve is a tool widely used by those who make monetary policy decisions or plan their investments according to valuation, negotiation, or coverage on financial instruments. Because of its importance, our interest is focused on evaluating the performance of a set of econometric models for adjustments in the term structure of interest rates (in the context of the public debt market bond rates in Colombia and United States) and on the possible forms that the yield curves can take. The results reveal the goodness-of-fit of the artificial neural networks (ANN), the Svensson curve, the Nelson-Siegel curve, and local polynomials. Nevertheless, we strongly recommended the use the Svensson curve in the estimation of interest rates, due to the interpretability of its parameters and its superiority over the Nelson-Siegel Curve.
Key words: yield curves, Nelson-Siegel, Svensson, Kernel regression, smooth splines, local polynomials, Friedmann supersmoother, trigonometric polynomials, artificial neuronal networks. JEL: C29, C51, C45, C53.
Résumé
La courbe de rendements est un outil utilisé amplement, par ceux qui prennent les décisions de politique monétaire ou planifient leur investissement, par le biais de l'évaluation, la négociation ou la couverture des instruments financiers. Étant donné son importance, l´intérêt de l´article est d´évaluer la performance de l'ensemble de modèles économétriques dans l'ajustement de la structure des échéances des taux d'intérêt (dans le cas du marché de dette publique en Colombie et aux États-Unis), et dans les différents formes qui peuvent prendre les courbes de rendements. Les résultats révèlent les bontés dans l'ajustement des réseaux neuronaux artificiels (RNA), la courbe de Svensson, la courbe de Nelson-Siegel et les polynômes locaux. Néanmoins, il est conseillé d'utiliser la courbe de Svensson dans l'estimation des taux d'intérêt, compte tenu de la facilité d´interprétation de ses paramètres et sa supériorité par rapport à la courbe de Nelson-Siegel.
Mot clés : courbe de rendements, Nelson-Siegel, Svensson, régression Kernel, polynômes locaux, super-lisseur de Friedmann, polynômes trigonométriques, réseaux neuronaux. JEL : C29, C51, C45, C53.
Las investigaciones en el contexto macroeconómico incorporan el estudio de la inflación, el crecimiento, el empleo, la tasa de cambio, la balanza comercial, la tasa de interés, entre otros. Se destaca esta última debido a que es usual asociar el término en singular (tasa de interés), a un tema que lejos de ser un precio unitario, constituye un elemento fundamental, con un contenido de información económica y financiera relevante para la toma de decisiones.
Por ejemplo, después de los trabajos seminales de Estrella y Hardouvelis (1989) se ha comprobado que la geometría de la curva de rendimientos en los mercados desarrollados incorpora información relevante para la predicción de las recesiones económicas. De igual manera, en finanzas la curva de rendimientos se convierte en un vector de precios de referencia importante para la fijación de las tasas de interés a diferentes plazos y por riesgo de crédito para bancos, prestamistas, colocadores de bonos y, en general, para todos los participantes del mercado de dinero.
En consecuencia, la curva de rendimientos tiene una importancia capital para el mundo académico y práctico desde el punto de vista económico y financiero, al reflejar el precio intertemporal del dinero. No obstante, a pesar de su importancia, la curva de rendimientos presenta empíricamente una serie de dificultades, debido a que se construye a través de una serie de precios (tasas) de instrumentos financieros discontinuos en el tiempo que, por lo general, están lejos de ser una "curva" suave. Por ejemplo, en el mercado local, el gobierno colombiano emite títulos de deuda de la Tesorería General de la Nación (TES); este mercado se compone de bonos con cupón a vencimientos que van desde 2 meses hasta 15 años. Es así que, se denomina curva en realidad a una nube de puntos que relaciona plazos con tasas de interés. Una descripción extensa referente a las teorías económicas que explican las formas asumidas por las curvas de rendimientos y su importancia en el contexto colombiano es presentada por Cámaro, Casas y Jiménez (2006).
Al graficar la curva obtenemos una figura discontinua, sin embargo, los contratos así como las transacciones económicas no se realizan de forma estandarizada. Es poco probable que una empresa o agente necesite o esté dispuesto a prestar capital a plazos equivalentes a los del gobierno nacional, por lo que se requieren instrumentos matemáticos para estimar curvas suaves que proyecten las tasas de interés en diferentes momentos del tiempo.
Aunque los TES o los bonos gubernamentales de cada país pueden proporcionar precios de referencia, existen otros campos en los que es necesario disponer de métodos matemáticos precisos que ajusten a través de una curva, las tasas de interés con relación al tiempo. Es el caso de la valoración de inversiones como bonos (por ejemplo, la Curva de Nelson y Siegel de la Bolsa de Valores de Colombia -BVC-) o la valoración de derivados de tasas de interés, siendo este último un mercado que hasta el momento no existe en Colombia, pero que seguramente será una senda hacia la cual converja el desarrollo del mercado local de capitales en el mediano y largo plazo.
Conscientes de lo anterior, el artículo tiene por objeto presentar, aplicar y discutir diferentes metodologías para la estimación de curvas de rendimientos, resaltando las bondades de cada una. El documento se compone de cinco partes, iniciando con la presente introducción; en la segunda y tercera sección se discuten las metodologías paramétricas y no paramétricas a ser utilizadas en este artículo; en la cuarta sección se realizan las simulaciones en el contexto de los bonos de deuda pública colombiana y estadounidense. Las gráficas de cada análisis fueron ubicadas en los anexos, con el objetivo de facilitar la lectura del documento. Finalmente, en la quinta sección se concluye con los modelos que se consideran apropiados para el ajuste de la curva de rendimientos, según algunos criterios de bondad de ajuste.
METODOLOGÍAS PARAMÉTRICAS
Estadísticamente, un modelo paramétrico es una familia funcional que obedece al comportamiento de alguna distribución de probabilidad, sobre la cual suponemos que las características de la población de interés pueden ser descritas. Es así como, los modelos diseñados en este contexto, basados en regresión, buscan describir el comportamiento de una variable de interés con otras llamadas exógenas, a través de funciones de vínculo lineales o no lineales.
La curva de Nelson-Siegel
Nelson y Siegel (1987) introducen un modelo paramétrico para el ajuste de los rendimientos hasta la madurez de los bonos del tesoro de Estados Unidos que se caracteriza por ser parsimonioso y flexible en modelar cualquier forma típica asociada con las curvas de rendimientos. La estructura paramétrica asociada a este modelo permite analizar el comportamiento a corto y a largo plazo de los rendimientos y ajustar -sin esfuerzos adicionales-, curvas monótonas, unimodales o del tipo S.
Una clase de funciones que genera fácilmente las formas usuales de las curvas de rendimientos es la asociada con la solución de ecuaciones en diferencia. La teoría de expectativas sobre la estructura de las tasas de interés promueve la investigación en este sentido, dado que si las tasas spot son producidas por medio de una ecuación diferencial, entonces las tasas forward -siendo pronósticos-, serán la solución de las ecuaciones diferenciales. La expresión paramétrica propuesta por Nelson y Siegel (1987) que describe las tasas forward es exhibida a continuación:
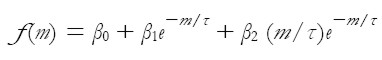 | [1] |
donde m denota la madurez del activo y β0, β1, β2 y τ los parámetros a ser estimados. Puesto que las tasas spot pueden ser obtenidas a través de tasas forward por medio de la expresión:
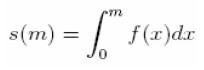 |
la ecuación que determina las tasas spot s(m) de activos con madurez m es dada por:
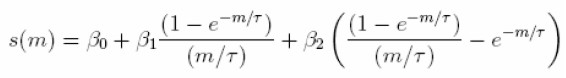 | [2] |
cuya ecuación es lineal si conocemos τ.
El valor límite del rendimiento es β0 cuando el plazo al vencimiento m es grande, mientras que, cuando el plazo al vencimiento m es pequeño el rendimiento en el límite es β0 + β1. Igualmente, los coeficientes del modelo de tasas forward pueden ser interpretados como medidas de fortaleza al corto, mediano y largo plazo. La contribución al largo plazo es determinada por β0, β1 lo hace al corto plazo ponderado por la función monótona creciente (decreciente)e-m/τ cuando β1 es negativo (positivo) y β2 lo hace al mediano plazo ponderado por la función monótona creciente (decreciente) (m/τ )e-m/τ cuando β2 es negativo (positivo). Una de las principales utilidades de la curva ha sido para propósitos de control de la política monetaria.
Consecuentemente, s(m) será la ecuación utilizada para captar la relación subyacente entre los rendimientos y los plazos al vencimiento o madurez, sin recurrir a modelos más complejos que involucren un mayor número de parámetros. Adicionalmente, dado que la curva de Nelson-Siegel proporciona tasas spot compuestas continuas, estas deben transformarse en cantidades discretas, a través de la función de descuento.
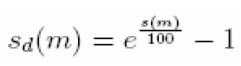 |
La curva de Svensson
En la curva de Nelson-Siegel se destaca que cada coeficiente del modelo contribuye en el comportamiento de las tasas forward en el corto, mediano y largo plazo; no obstante, Svensson (1994) propone una nueva versión de la curva de Nelson-Siegel donde un cuarto término es incluido para producir un efecto adicional y semejante al proporcionado por β2: β3(m/τ2)e-m/τ2.
En este caso, la función para describir la dinámica de las tasas forward es
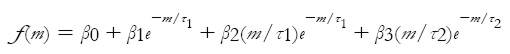 | [3] |
La curva spot de Svensson puede ser derivada a partir de la curva forward en forma semejante a la descrita para el modelo de Nelson-Siegel, obteniendo la siguiente expresión:
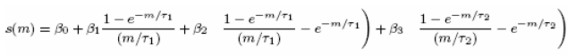 | [4] |
La función de descuento tiene que ser utilizada con el fin de obtener las tasas estimadas para cada día de negociación o trading. Svensson (1994) propone estimar los parámetros de la curva cero cupón (curva spot), minimizando una medida de ajuste tal como la suma de cuadrados del error sobre los precios spot; sin embargo, enfatiza en que los precios pueden llegar a ser mal ajustados para los activos de madurez corta. En lugar de llevar el análisis por este camino, propone estimar los rendimientos fundamentado, principalmente, en que las decisiones de la política económica se basan en el comportamiento de las tasas y que obteniendo las tasas a través de la curva, los precios pueden ser calculados una vez la función de descuento es evaluada. De esta manera, los parámetros son escogidos minimizando la suma de cuadrados de la diferencia entre los rendimientos observados y estimados por la curva.
La estimación es realizada por medio de máxima verosimilitud, mínimos cuadrados no lineales o el método de momentos generalizados. En muchos casos, como afirma Svensson (1994), el modelo de Nelson-Siegel proporciona ajustes satisfactorios, aunque en algunos casos cuando la estructura de las tasas de interés es más compleja, el ajuste del modelo de Nelson-Siegel es poco satisfactorio y el modelo de Svensson logra desempeñarse mejor.
Polinomios de componentes principales
Hunt y Terry (1998) propone un ajuste de la curva de rendimientos utilizando polinomios. Si frecuentemente la curva es especificada como:
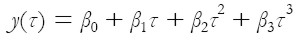 | [5] |
La cual puede captar todas la formas que puede asumir la curva, su principal problema recae en el ajuste para aquellas tasas con períodos de vencimiento bastante largos. Aunque los autores conocen sobre las propiedades de parsimonia y de ajuste asociados con la curva de Nelson-Siegel, critican los problemas que acarrea la estimación de sus parámetros, proponiendo el ajuste de la curva de polinomios, bajo algunas modificaciones.
Una transformación sobre el término de plazos (τ) que remueve la inestabilidad asociada con las tasas a largo plazo del polinomio (5) es sugerida. El modelo recomendado, siguiendo la notación de Hunt y Terry (1998) es:
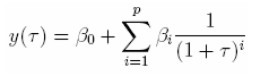 | [6] |
donde
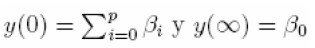 |
Investigaciones relacionadas con curvas de rendimientos, han llegado a la conclusión que modelos con tres o cuatro parámetros son suficientes para obtener un buen ajuste de los datos (Hunt 1995). Por tal motivo, Hunt y Terry (1998) proponen restringir p a tres o cuatro. Aunque este número de parámetros no necesariamente determina si realmente la bondad de ajuste pueda llegar a ser satisfactoria, los autores proponen utilizar componentes principales sobre los primeros p términos polinomiales 1/(1 + τ), con el fin de seleccionar k < p variables, a ser incluidas en la ecuación (6). Utilizar las componentes principales proporcionará un menor error de ajuste en comparación con (5), debido a su capacidad para captar variabilidad. Una descripción detallada respecto al cálculo de las componentes principales en el esquema polinomial es dada por Hunt y Terry (1998).
Polinomios trigonométricos
Las funciones trigonométricas pueden ser utilizadas para capturar de forma satisfactoria las distintas configuraciones que pueden asumir las curvas de rendimientos. En este caso, el modelo puede ser descrito como y(τ ) = β0 + β1cos(γ1 τ ) + β2sen(γ2 τ); donde τ representa la duración o la madurez del papel, en tanto que β0, β1, β2, γ1 y γ2 son los parámetros objeto de interés. Cualquier metodología de optimización no lineal puede ser utilizada para estimar los parámetros del modelo (Nocedal y Wright 1999). Aunque podría asumirse un parámetro de fase en el modelo, este no es considerado por motivos de parsimonia.
METODOLOGÍA NO-PARAMÉTRICA
La regresión no paramétrica se ha convertido en los últimos años en un área de excesivo estudio, debido a sus ventajas relativas respecto a los modelos de regresión basado en funciones. Entre las características más importantes de estos modelos tenemos, la flexibilidad en los supuestos y el ajuste dirigido específicamente a través de los datos.
Dentro de un marco estadístico supondremos que tenemos un conjunto de n observaciones (xi, yi), i= 1, 2,..., n, independientes, donde se intenta establecer las relaciones existentes entre una respuesta y un conjunto de variables explicativas de forma semejante a los modelos de regresión clásica.
El modelo que relaciona este conjunto de variables es dado por:
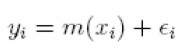 |
donde la función m(.) no específica una relación paramétrica, sino permitir que los datos determinen la relación funcional apropiada. Bajo estas condiciones la idea es que la media m(.) sea suave, suavidad que puede controlarse acotando la segunda derivada, | m" (x)| ≤ M, para todo x y M una constante.
Regresión Kernel
El método más simple de suavizamiento es el suavizador Kernel. Un punto x se fija en el soporte de la función m(.) y una ventana de suavizamiento es definida alrededor de x. Frecuentemente, la ventana de suavizamiento es simplemente un intervalo de la forma (x - h, x + h), donde h es un parámetro conocido como bandwidth.
La estimación Kernel es un promedio ponderado de las observaciones dentro de la ventana de suavizamiento
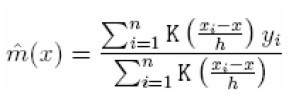 | [7] |
donde K(.) es la función Kernel de ponderación. La función Kernel es escogida de tal forma que las observaciones más próximas a x reciben mayor peso. Una función frecuentemente utilizada es la bicuadrática:
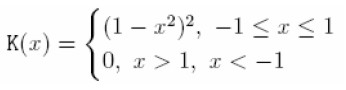 |
Sin embargo, otro tipo de funciones de peso son utilizadas, tal como la gaussiana, K(x) = (2 √ π ) - 1 e x² / 2 y la familia beta simétrica 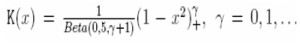
Note que cuando escogemos γ = 0, 1, 2 y 3 obtenemos las funciones Kernel uniforme (Box), de Epanechnikov, la bipeso y la tripeso, respectivamente.
El suavizador Kernel puede ser representado como
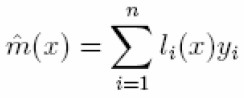 | [8] |
donde
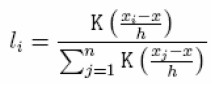 |
La estimación Kernel en (7) es llamada la estimación de Nadaray- Watson, en honor a sus creadores. Su simplicidad lo hace de fácil comprensión e implementación; no obstante, se sabe que los ajustes en los extremos son sesgados. Una referencia ideal para un desarrollo más completo sobre este tema puede encontrarse en Fan y Gijbels (1996).
Polinomios locales
Conocida también como regresión local, la idea es aproximar la función suave m(.) por medio de un polinomio de bajo orden en una vecindad entorno de un punto x. Por ejemplo, una aproximación lineal local es m(xi ) ≈ a0 + a1 (xi - x), para x - h ≤ xi ≤ x + h. Una aproximación local cuadrática es: 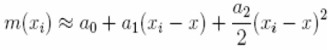
La aproximación local puede ser ajustada a través de mínimos cuadrados ponderados localmente. Una función Kernel y un bandwidth son definidos omo en la regresión Kernel. Los coeficientes â0 y â1, son escogidos de tal forma que se pueda minimizar la expresión:
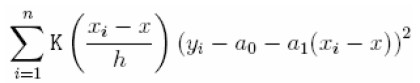 | [9] |
Reescribiendo (9) en términos matriciales obtenemos:
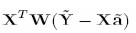 |
Donde X es la matriz diseño para cada regresión lineal, â el vector de parámetros, W la matriz diagonal de pesos K ( xi - x / h ) y Ÿ el vector de observaciones de orden n.
El vector de parámetros estimado está dado por 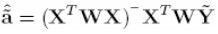 y en forma semejante con (8), tenemos que:
y en forma semejante con (8), tenemos que: 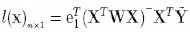 donde e T i es un vector de ceros de tamaño n, exceptuando la primera entrada cuyo valor es 1.
donde e T i es un vector de ceros de tamaño n, exceptuando la primera entrada cuyo valor es 1.
Finalmente, la selección del h está basado en procedimientos de bondad de ajuste que permite obtener el mejor modelo. Entre los más utilizados sobresalen los métodos de validación cruzada generalizada y plug-in, los cuales son descritos detalladamente en Fan y Gijbels (1996).
Splines suavizados1
Las funciones polinomiales se caracterizan por tener todas las derivadas en cualquier punto de su soporte; no obstante, cuando ciertas funciones no poseen un alto grado de suavidad en determinados puntos, el ajuste debido a estas funciones de polinomios no siempre será satisfactoria en estos tramos.
Para sobrellevar esta desventaja, el ajuste de polinomios de bajo orden localmente, con discontinuidades en ciertos puntos (knots), resulta en el conocido método de splines.
Splines de polinomios
Suponga que queremos aproximar la función m(.) por una función spline. Frecuentemente, el spline cúbico es utilizado para esta aproximación, sin embargo, otro tipo de splines pueden ser definidos.
Siguiendo la notación de Fan y Gijbels (1996), sea t1, t2, t3, ... , tJ el conjunto de nodos o knots en orden creciente, tal que en cada intervalo (-∞, t1], [t1, t2],... , [tJ-1, tJ], [tJ, ∞), funciones cúbicas continuas diferenciables son ajustadas. En este caso el espacio parámetrico es (J+4)-dimensional.
Un conjunto de splines cúbicos son ampliamente utilizados en la obtención de la función de splines
Base de potencias:donde x+ es la parte positiva de x. Así por ejemplo, la función de suavizamiento puede ser expresada como:
[10]
siendo Bj (x), j = 1, 2,... , J + 4, la base polinomial descrita anteriormente.
Los regresores definidos de esta forma pueden ocasionar problemas de estimación (multicolinealidad), motivo por el cual, los Bj(x) son redefinidos como 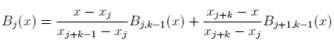 , suponiendo que Bj,1 = 1 para xj ≤ x ≤ xj+1 y cero en caso contrario. El proceso de estimación de (10) es realizado a través de mínimos cuadrados penalizados (ver la siguiente sección).
, suponiendo que Bj,1 = 1 para xj ≤ x ≤ xj+1 y cero en caso contrario. El proceso de estimación de (10) es realizado a través de mínimos cuadrados penalizados (ver la siguiente sección).
Adicionalmente, una desventaja del método, es su sensibilidad al número y ubicación de los nodos, motivo por el cual han sido propuestos diferentes procedimientos para su selección.
Splines suavizados
El proceso de suavizamiento a través de este método está basado en la minimización de la función:
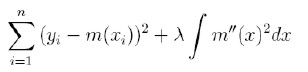 |
donde λ es una constante especificada de suavizamiento. El mecanismo de optimización intenta crear un balance entre el sesgo de estimación y la suavidad de la curva ajustada. El parámetro λ puede asumirse variable (Abramovich y Steinberg 1996) y estimado a través de validación cruzada generalizada.
Supersuavizador de Friedmann
Las metodologías usuales de suavizamiento asumen que el parámetro suavizador es constante, factor que sumado a la forma de la curva subyacente puede hacer que surjan problemas, tal como el aumento en la varianza de la componente del error y/o a variaciones incontrolables de la segunda derivada de la función subyacente sobre el conjunto predictor. El suavizador propuesto por Friedman (1984) intenta corregir estos problemas, asumiendo que el bandwidth es variable sobre el conjunto de predictores.
Formalmente, se puede estimar un bandwidth para cada x, al igual que el correspondiente valor óptimo de suavizamiento, minimizando la expresión: e²(m,h)=E( Y - m( X | h( X)))² con respecto a las funciones m(x) y h(x). La anterior expresión puede reescribirse como:
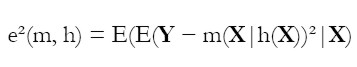 | [11] |
de tal forma que podemos minimizar el error con respecto a m y h para cada valor de x.
Como en el caso del bandwidth constante, se comienza aplicando un suavizador lineal local muchas veces sobre diferentes valores discretos de h, 0 < h < n. Friedman (1984) propone utilizar tres conjuntos de valores, h=0,05n, h=0,2n y h=0,5n, los cuales llama suavizadores "tweeter", "midrange" y "woofer", respectivamente.
Para estimar (11) se utiliza el residual de la validación cruzada (12) cuya descripción completa puede encontrarse en Friedman (1984)
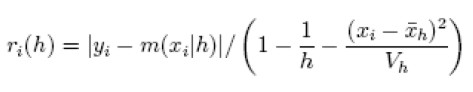 | [12] |
siendo 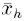 y Vh, la media y varianza de los x, bajo un h preeestablecido. Igualmente, Friedman (1984) aconseja suavizar | ri (h)| contra xi, utilizando los ê(m, h| xi), en procura de seleccionar la mejor amplitud de intervalo o bandwith: ê ( m, hvc(xi) | xi ) = minh ê(m, h | xi ), donde hvc ( xi ) es el mejor bandwidth bajo la validación cruzada respecto a cada xi , mientras que h toma los valores de los suavizadores antes definidos.
y Vh, la media y varianza de los x, bajo un h preeestablecido. Igualmente, Friedman (1984) aconseja suavizar | ri (h)| contra xi, utilizando los ê(m, h| xi), en procura de seleccionar la mejor amplitud de intervalo o bandwith: ê ( m, hvc(xi) | xi ) = minh ê(m, h | xi ), donde hvc ( xi ) es el mejor bandwidth bajo la validación cruzada respecto a cada xi , mientras que h toma los valores de los suavizadores antes definidos.
De esta manera, el mejor valor suavizado dado xi, siguiendo la notación de Friedman (1984), s*(xi), estará asociado con el bandwidth: "tweeter", "midrange" o "woofer" que minimice el error bajo la validación cruzada. Es posible a través de esta metodología obtener para cada vecindad en torno a xi diferentes bandwith y suavizados que proporcionan resultados óptimos, por tal razón, Friedman (1984) propone seleccionar la mejor amplitud de intervalo, suavizando los hvc (xi) contra xi utilizando el suavizador "midrange", mientras que la curva estimada es obtenida interpolando entre los dos suavizadores con los bandwith estimados más parecidos.
Una suposición general establece que la curva subyacente que describe el comportamiento de los datos es suave, así que sería posible modificar el bandwidth en procura de un mayor suavizamiento, sacrificando exactitud numérica. Con este fin, Friedman (1984) propone un método de cálculo del bandwidth:
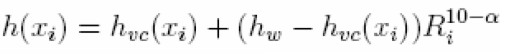 |
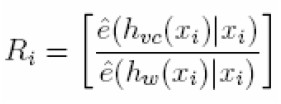 | [13] |
donde 0 < ∞ < 10, hw es la amplitud calculada utilizando el suavizador "woofer" y hvc (·) la amplitud obtenida bajo la validación cruzada para cada observación. Sin importar el α, cuando la contribución relativa de cada una de estas amplitudes no difiere significativamente, la amplitud de intervalo o bandwidth seleccionada es la determinada por el suavizador "woofer"; no obstante, si la eficiencia relativa está asociada con la amplitud bajo la validación cruzada, entonces, la ecuación en proporcionará esta amplitud. En otros casos, dependiendo del desempeño relativo y el parámetro α definido por el usuario, la ecuación proporcionará una amplitud, resultado de la combinación lineal entre el suavizador "woofer" y el obtenido bajo validación cruzada.
Una vez el bandwidth de suavización variable ha sido obtenido, los siguientes pasos son realizados sobre el conjunto de observaciones:
1. Suavice los datos con los bandwidth "tweeter", "midrange" y "woofer".
2. Suavice los residuales absolutos (12) obtenidos bajo cada bandwidth en el paso anterior, utilizando una amplitud de intervalo "midrange".
3. Seleccione el mejor bandwidth para cada observación, minimizando el error sobre la salida del paso (2).
4. Suavice los mejores bandwidth estimados en el paso (3) utilizando amplitud de intervalo "midrange".
5. Utilice los bandwidth suavizados para interpolar entre los valores suavizados obtenidos en el paso 1.
Las principales deficiencias atribuidas a esta técnica están asociadas con la pérdida de independencia entre los residuales εi relativo al orden de los predictores xi, subestimando (sobreestimando) cuando la correlación es positiva-alta (negativa-alta).
Redes neuronales artificiales
Los recientes desarrollos investigativos han mostrado la capacidad de las redes neuronales para la detección de patrones, clasificación y predicción a través del aprendizaje por medio de la experiencia. Su importancia actual, sin lugar a dudas, es consecuencia del desarrollo computacional, punto de partida para su divulgación, desenvolvimiento teórico y práctico en diversos campos del conocimiento.
Una de las mayores áreas de aplicación de las redes neuronales es la predicción (Sharda 1994). Dentro de este contexto, las redes resultan ser una herramienta atractiva para los investigadores, comparada con las metodologías tradicionales basada en modelos de funciones.
Las redes neuronales artificiales intentan emular el comportamiento biológico del cerebro humano. Como sabemos, el cerebro humano es un conjunto complejo de interconexiones de elementos simples llamados nodos o neuronas. Cada nodo recibe una señal de entrada proveniente de otros nodos o a través de estímulos externos; localmente el nodo procesa la información recibida por medio de una función de transferencia o activación y produce una señal de salida transformada, que irá hacia otros nodos o como una respuesta, consecuencia de un estímulo. Aunque cada nodo individualmente no proporciona información realmente valiosa, en conjunto, pueden realizar un sorprendente número de tareas de forma eficiente. Esta característica hace de las redes neuronales un mecanismo poderoso computacionalmente para aprender a partir de ejemplos y después generalizar para casos nunca antes considerados.
Aunque diferentes arquitecturas de redes neuronales han sido propuestas (Haykin 1994), la más utilizada es la red multilayer Perceptron (MLP). Una red MLP está compuesta de varias capas y nodos o neuronas. Los nodos de la primera capa son los encargados de recibir la información del exterior, mientras que la última capa es encargada de proporcionar la respuesta asociada a esta información. Entre estas dos capas puede haber innumerables capas y nodos. Adicionalmente, los nodos de capas adyacentes están completamente conectados; la Figura 1 exhibe una MLP con todas las conexiones entre los nodos de cada capa.
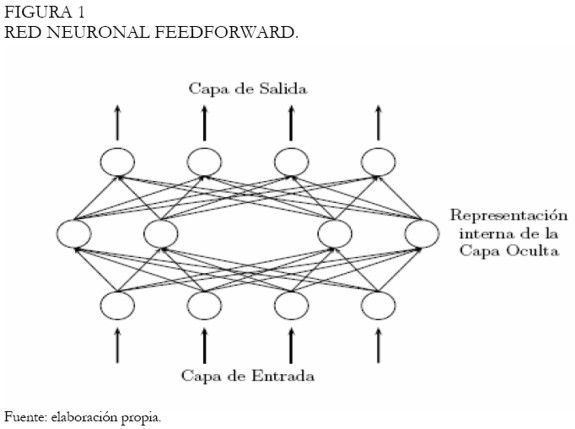 |
Para un problema de pronóstico con redes neuronales, las entradas a la red son asociadas con variables independientes o explicativas. En este caso la relación funcional estimada establecida por la red neuronal será de la forma yt = f (x1, x2,..., xp); donde x1, x2,..., xp son p variables exógenas y y una variable endógena. En este sentido la red es equivalente a un modelo de regresión no lineal. Igualmente, en el contexto del pronóstico de series temporales, las entradas de la red son series rezagadas de la original y la salida representa su valor futuro. En este caso la red haría un mapeo de la siguiente forma yt = f (yt-1, yt-2, ..., yt-p); donde yt es la observación en el tiempo t. Bajo estas características la red asemeja un modelo autorregresivo en el pronóstico de series temporales. Una discusión respecto a la relación existente entre las redes neuronales y la metodología de Box-Jenkins es dada por Suykens, Vandewalle y Moor (1996).
Antes de que la red sea utilizada para realizar alguna tarea específica, debe ser entrenada. Básicamente, entrenar es el proceso de determinar los pesos (eje central de la red neuronal). El conocimiento aprendido por la red es almacenado en cada una de los arcos que representan las conexiones entre los nodos. Es a través de estas conexiones que las redes pueden realizar complejos mapeos no lineales desde los nodos de entrada hasta los nodos de salida. El entrenamiento de la MLP es supervisado, caso en el cual la respuesta deseada o valor objetivo para cada patrón de entrada o ejemplo está siempre disponible.
Los datos de entrenamiento son ingresados a la red en forma de vectores de variables o como patrones de entrada. Cada elemento en el vector de entrada es asociado con un nodo de la capa de entrada; de esta forma, el número de entradas a la red es igual a la dimensión del vector de entrada. Para el pronóstico de series temporales el número de variables de entrada es difícil de establecer, no obstante, una ventana de rezagos fija es constituida a lo largo de la serie. El total de datos disponible es usualmente dividido en un conjunto de entrenamiento y otro de prueba. El primero es utilizado para estimar los pesos de la red, mientras que el segundo es empleado para evaluar la capacidad de generalización de la red.
Para el proceso de entrenamiento, patrones de entrada son ingresados a la red. Los valores de activación de los nodos de entrada son multiplicados por su peso respectivo y acumulados en cada nodo sobre la primera capa. El total es evaluado en una función de activación y asumido como la salida del respectivo nodo. A esta salida algunos investigadores la identifican como la activación del nodo y es la entrada de otros nodos en capas siguientes de la red hasta que los valores de activación de la salida sean encontrados. El algoritmo de entrenamiento es utilizado para encontrar los pesos que minimicen una medida global de error tal como la suma de cuadrados del error (SSE).
En el pronóstico con series temporales, un patrón de entrenamiento consiste de un conjunto de valores fijos de variables en rezago de la serie. Suponga que tenemos N observaciones y1, y2, ..., yN para el proceso de entrenamiento y se requiere pronosticar un paso al frente, entonces con una red neuronal de n nodos de entrada, tenemos N - n patrones de entrenamiento. El primer patrón de entrenamiento estará conformado por y1, y2, ..., yn como las entradas y yn+1 como el valor objetivo. El segundo patrón de entrenamiento será y2, y3, ..., yn+1 y el valor de salida deseado yn+2. Finalmente, el último patrón de entrada será yN-n, yN-n+1, ..., yN-1 y yN el valor objetivo. Frecuentemente, una función objetivo basada en la SSE es minimizada durante el proceso de entrenamiento
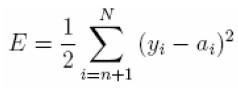 |
donde ai es la salida actual de la red.
Una descripción más detallada sobre las diferentes arquitecturas de red existentes, el número óptimo de capas ocultas y neuronas, las funciones de activación más utilizadas, los algoritmos de entrenamiento, la normalización de los datos, como también de otros temas relacionados con sus ventajas y deficiencias (Haykin 1994, Kaastra y Boyd 1996, Zhang, Patuwo y Hu 1998, Isasi y Galván 2004), entre otros.
Implementación de las curvas en Colombia
Los organismos de control de los mercados financieros en Colombia empezaron a implementar desde mediados de 1996 la curva cero cupón para el mercado de deuda pública, basado en la metodología de McCulloch (1971), con el objetivo de proporcionar un indicador sobre las rentabilidades de los papeles negociados en el mercado secundario, que les permitiera a los agentes financieros tomar ventaja al momento de efectuar un negocio de compra o venta.
En ese mismo año, tras los encuentros de los bancos centrales europeos en Basilea con el BIS (Bank of International settlements), fueron discutidas metodologías econométricas implementadas por los diferentes bancos, quienes estuvieron de acuerdo en que las curvas de Nelson-Siegel y Svensson son de fácil interpretabilidad y compresión para el análisis de las tasas de interés (BIS 2005). En Colombia, no fue sino hasta mediados de 1999 que la Bolsa de Bogotá empieza a hacer pública la curva de rendimientos para los papeles del mercado de TES tasa fija (CETES) (BVC 2002).
Entre el 2001 y 2002 se dio un mayor desarrollo investigativo en esta línea, con trabajos del Banco de la República orientados a utilizar las funciones de Nelson-Siegel y splines cúbicos suavizados (Arango, Melo y Vásquez 2002, Melo y Vásquez 2002, y Julio, Mera y Revéiz 2002), con la finalidad de proporcionar metodologías que estimaran de forma óptima, la curva cero cupón de los títulos de deuda pública.
La investigación de Arango et al. (2002) concluye que utilizar la metodología de Nelson-Siegel para estimar la curva de TES tasa fija, supera ampliamente a la curva CETES (metodología basada en los splines de McCulloch 1971), que venía siendo utilizada por la BVC. Siguiendo en la línea del documento anterior, Melo y Vásquez (2002) amplían su estudio incluyendo los B-splines cúbicos en el análisis. En este documento concluyen que los B-splines ajustan la curva de TES tasa fija en forma semejante a la función de Nelson-Siegel, superando las dos, el desempeño de los splines de McCulloch.
En la investigación de Julio et al. (2002) la curva de TES tasa fija es estimada a través de diferentes métodos: splines suavizados, cero cupón y bootstraping. Una sección del documento es dedicada a los key rate durations, cuyo objetivo es medir las sensibilidad del precio de un papel por segmentos de la curva de rendimientos, teniendo en cuenta que los movimientos en la curva no siempre son paralelos. Los autores concluyen que, aunque el abanico de modelos es extenso, los resultados que proporcione cada uno es importante en los procesos de decisión, haciendo notar que la eficacia del mercado es determinante en la calidad de los datos proporcionados por los métodos utilizados. Actualmente, la BVC pública diariamente las estimaciones de la curva de Nelson y Siegel para los TES tasa fija, TES indexados a la UVR y los CDTs.
IMPLEMENTACIÓN DE LAS METODOLOGÍAS PARAMÉTRICAS Y NO-PARAMÉTRICAS EN EL AJUSTE DE LA CURVA DE RENDIMIENTOS
Se evalúa el desempeño de cada uno de los modelos descritos en las secciones anteriores, con el objetivo de determinar la bondad de ajuste de cada uno en la estimación de las tasas de negociación de cierre del mercado secundario de TES tasa fija colombiano y tasas de negociación promedio del mercado de bonos de Estados Unidos2. Inicialmente, en el contexto colombiano, dos conjuntos de datos fueron analizados: i) las tasas de cierre correspondientes al día 30 de Marzo del 2006, fecha en la cual se registraron las tasas más bajas en 2006; y ii) las tasas de cierre del día 29 de junio del 2006, cuando se exhibieron las tasas más altas en los TES tasa fija en el mismo año.
Posteriormente, las tasas de los bonos del mercado de deuda pública estadounidense son analizadas en función de las diferentes formas que puede asumir la curva de rendimientos, características que permitirán comprobar el desempeño de cada una de las metodologías. Se escogió arbitrariamente la duración modificada3 como predictor de las tasas de los TES en Colombia y los días al vencimiento anualizados en el caso de Estados Unidos.
La intención de este documento es ampliar el análisis de las curvas de rendimiento, recurriendo a otras técnicas existentes en la estadística y/o econometría, que en el contexto colombiano no han sido analizadas y que podrían hipotéticamente superar las metodologías utilizadas en la actualidad o contribuir en el desarrollo teórico de las curvas de rendimientos. Los modelos ampliamente reseñados en las investigaciones colombianas han sido la curva de Nelson-Siegel y los splines suavizados, entre los que se incluyen los suavizadores de McCulloch (1971)4.
El aporte de este artículo aporte incluye el análisis de la regresión Kernel, los polinomios locales, la curva de Svensson, el suavizador de Friedman y los polinomios con componentes principales. El paquete estadístico utilizado para el análisis fue R5, el cual tiene implementado una gran variedad de las metodologías antes descritas; no obstante, las curvas de Nelson-Siegel y Svensson fueron programadas6.
Análisis de los TES tasa fija (30 de marzo de 2006)
En esta fecha, el mercado de TES tasa fija experimentó las tasas más bajas, resultado de las expectativas sobre los datos revisados del crecimiento económico para el año 2005, que publicaría el DANE (Departamento Nacional de Estadística) en días siguientes y que registraron un crecimiento promedio del 5,2 % para el 2005.
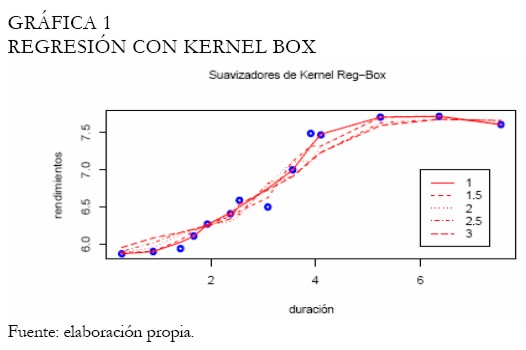
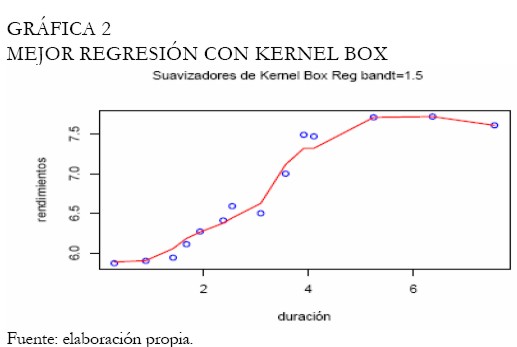
A continuación las curvas de rendimientos son ajustadas para este conjunto de tasas, con el fin de evaluar cuál es la metodología de mejor desempeño. El Anexo 1 contiene las figuras resultado del análisis; inicialmente, la curva ajustada bajo regresión Kernel es exhibida en la Gráfica 1. El Kernel utilizado es el Box, con 5 diferentes bandwidth, no obstante, con una amplitud de 1,5 se consigue apreciar el mejor ajuste visualmente; la Gráfica 2 muestra la curva ajustada para esta amplitud de intervalo o bandwidth. Note que, las otras amplitudes consiguieron mejorar el suavizamiento, sin embargo, sujeto a un incremento en el error de ajuste en las tasas de corto y mediano plazo. Se resalta que a una mayor amplitud de intervalo el mejor ajuste proporcionado por el método es la interpolación, así que, en el momento de modelar las tasas, debe encontrarse un equilibrio entre la bondad de ajuste y la suavidad de la curva.
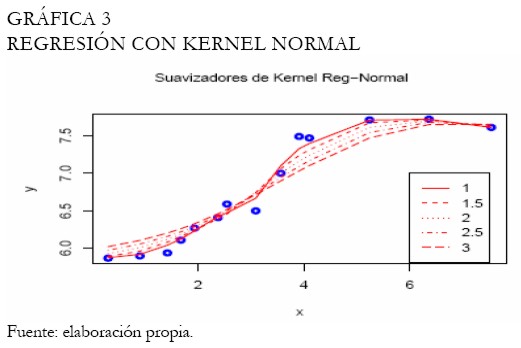
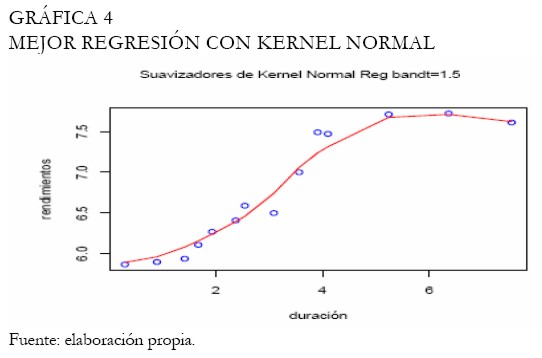
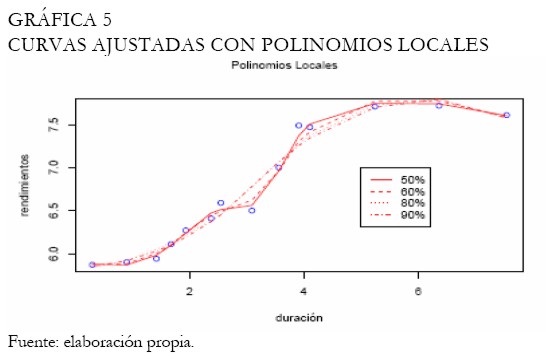
Se realiza nuevamente el análisis con la función Kernel gaussiana, ampliamente utilizada. La Gráfica 3 exhibe las curvas ajustadas con diferentes bandwidth, mientras que la Gráfica 4 exhibe la mejor curva ajustada, seleccionada entre las expuestas en la Gráfica 3. Se puede apreciar que el Kernel gaussiano o normal proporciona mejores resultados que el Kernel Box. Las curvas obtenidas bajo polinomios locales son expuestas en la Gráfica 5, considerando un abanico de bandwidth. En este caso, el mejor ajuste es decidido a través del cuadrado medio del error, teniendo en cuenta que al aumentar la amplitud del intervalo las curvas se hacen más suaves (Gráfica 5).
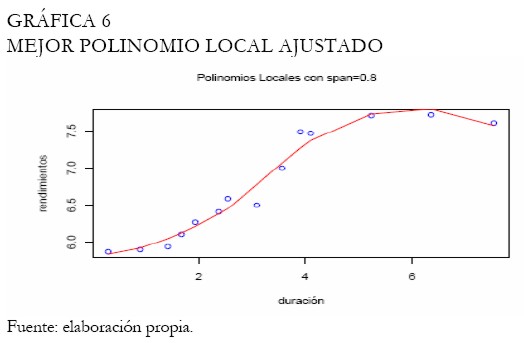
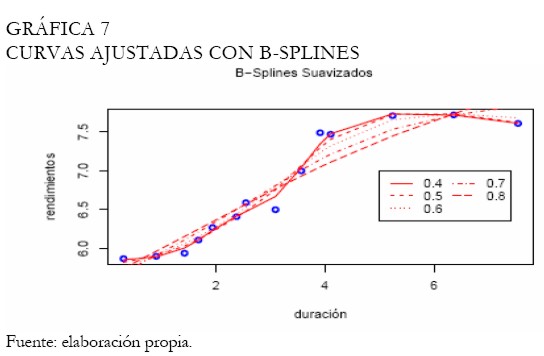
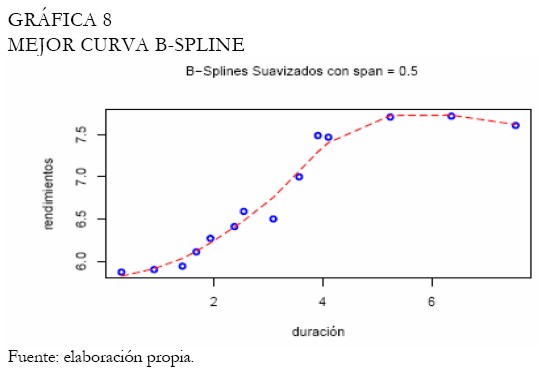
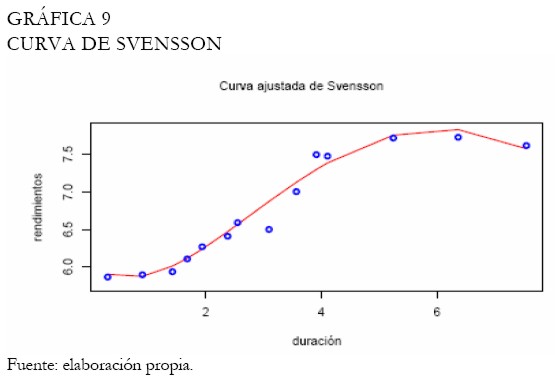
Bajo estas circunstancias, se intenta escoger la mejor amplitud balanceando entre suavidad y error mínimo (Gráfica 6). Con relación a los splines suavizados, los B-splines cúbicos son utilizados con diferentes amplitudes de intervalo (Gráfica 7). El proceso de selección del suavizamiento es realizado bajo el criterio de validación cruzada, obteniendo el mejor suavizamiento bajo la amplitud 0,5 (Gráfica 8), el cual registró la menor penalización y el menor criterio de validación cruzada respecto a las otras amplitudes. La curva de Svensson es ajustada, puesto que queremos evidenciar si la inclusión de parámetros adicionales relativa a la curva de Nelson-Siegel mejora el ajuste de los rendimientos de los TES tasa fija. Note que, los modelos no lineales de esta clase, durante el proceso de estimación son sensibles a los puntos iniciales. La Gráfica 9 exhibe la curva ajustada de Svensson. Los parámetros son estimados a través del método de optimización de Nelder-Mead (Venables y Ripley 2002), minimizando la suma de cuadrados del error.
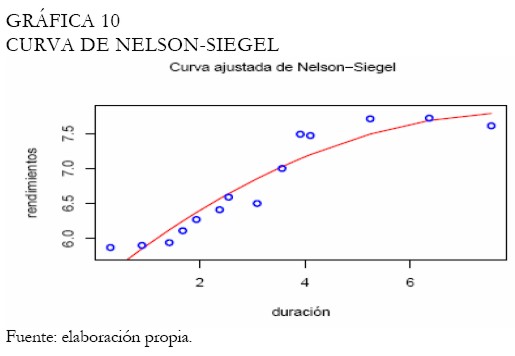
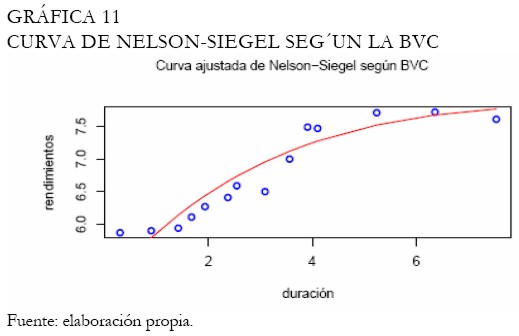
Por otro lado, la curva ajustada de Nelson-Siegel se muestra en la Gráfica 10. Note que, este ajuste no es satisfactorio en los extremos de la curva de rendimientos en comparación con la curva de Svensson. Adicionalmente, al graficar la curva de rendimientos sobre los parámetros estimados por la BVC, obtenemos un ajuste semejante (Gráfica 11). Aunque las muestras utilizadas por la BVC son diferentes a las consideradas en este artículo para el proceso de estimación de los parámetros de la curva (igualmente, el tiempo al vencimiento utilizado por la BVC son días, diferente a la duración modificada), un ajuste semejante es obtenido, evidenciando las bondades de la curva de Svensson sobre la de Nelson-Siegel, en este caso.
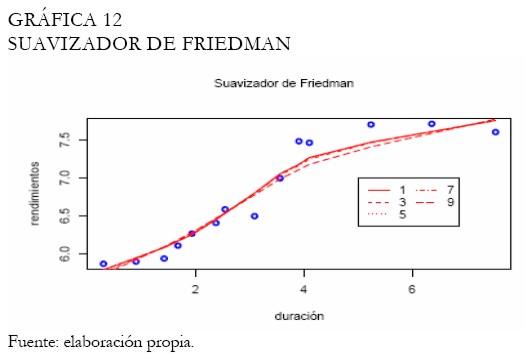
Haciendo uso del supersuavizador de Friedman, la curva de rendimientos es ajustada bajo diferentes niveles de suavidad en tanto que la amplitud de intervalo es seleccionada automáticamente a través de validación cruzada; la Gráfica 12 muestra los resultados. Puede observarse también en esta figura, que el suavizador de Friedman no consigue ajustar satisfactoriamente los extremos, especialmente, para los papeles con duraciones de mediano y largo plazo.
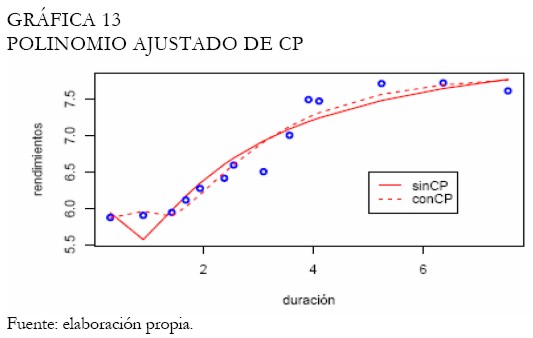
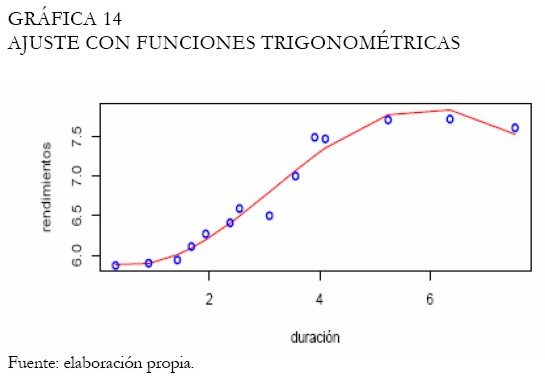
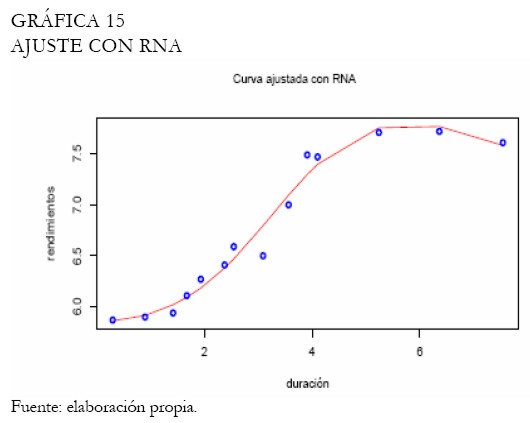
Por medio de polinomios con componentes principales (Hunt 1995), obtenemos la curva ajustada la cual es contrastada con el ajuste sin componentes principales (Gráfica 13). Puede observar la capacidad del modelo de componentes principales para ajustar las tasas del corto plazo. Técnicamente, partiendo de un polinomio de grado cuatro, dos componentes principales son seleccionados, explicando aproximadamente el 92 % de la variabilidad en las tasas de los TES tasa fija. El ajuste a través de funciones trigonométricas permite obtener la curva presentada en la Gráfica 14. Note que, el ajuste es satisfactorio en los extremos y la duración modificada se exhibe como un buen predictor. Con las redes neuronales se diseña una arquitectura MLP con momentum y una capa oculta que es suficiente para recoger la dinámica de las tasas de los TES; la Gráfica 15 presenta el ajuste.
Después de una descripción de cada una de las metodologías en consideración bajo el modelamiento, se evalúa numéricamente su capacidad de ajuste con el fin de determinar cuáles son los mejores métodos. Para tomar tal decisión, el cuadrado medio del error (MSE) y el error porcentual absoluto medio (MAPE) fueron utilizados. El Cuadro 1 exhibe los resultados ordenados de manera ascendente por MSE.
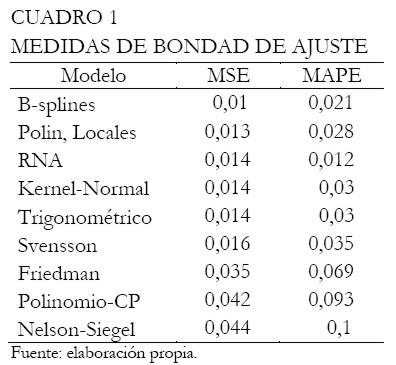 |
Note que los B-splines poseen el mejor ajuste, seguido por los polinomios locales y las redes neuronales (RNA). Por otro lado, la curva ajustada de Nelson-Siegel presenta un desempeño inferior al comparado con los otros modelos, por ejemplo, la curva de Svensson. A través del MAPE, las redes neuronales exhiben el mejor desempeño, seguido por los B-splines y los polinomios locales.
Análisis de los TES tasa fija (29 de junio de 2006)
Durante la jornada del 29 de junio del 2006, las tasas del mercado de deuda pública experimentaron las tasas más altas en 2006, consecuencia de las presiones inflacionarias latentes en la economía norteamericana que se hicieron evidentes a través del conocimiento para mayo del indicador líder PCE7 (Personal Consumation Expenditures), generando cierto temor en los mercados internacionales ante la posibilidad de un incremento en las tasas de interés por parte de la Reserva Federal.
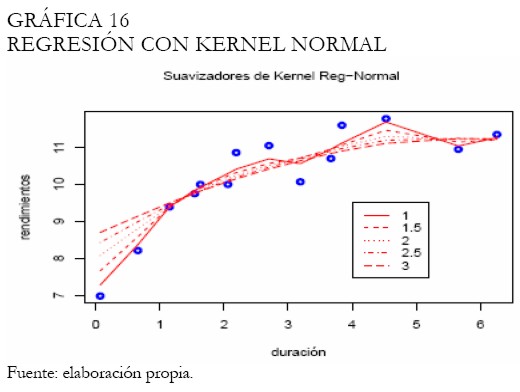
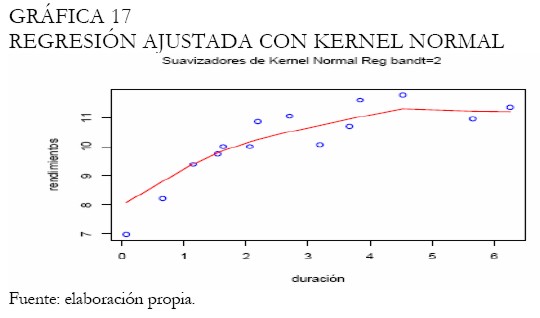
Un análisis semejante al efectuado para las tasas del 30 de marzo del 2006 fue realizado. El Anexo 2 contiene las figuras resultado del análisis. Inicialmente, la regresión Kernel es efectuada teniendo en cuenta la función Kernel normal, ampliamente utilizada en la práctica. El análisis gráfico permite deducir que con una amplitud del intervalo de 50%, (2 en la Gráfica ), se obtiene un resultado satisfactorio. La Gráfica 17 muestra la curva ajustada para esta amplitud; no obstante, el ajuste en la parte larga de la curva no luce muy suave, mientras que en la parte corta, no logra definir correctamente la tendencia.
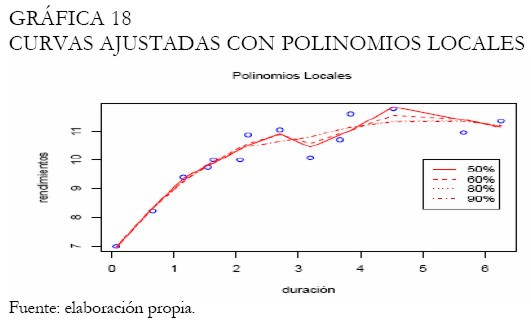
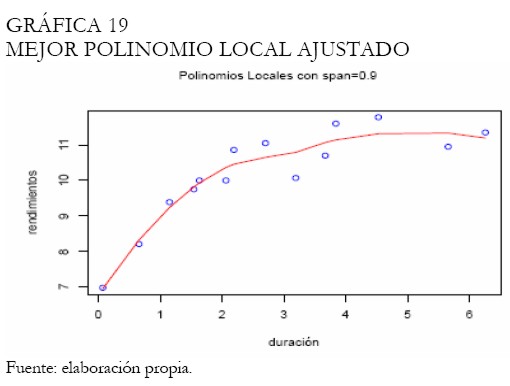
Con la metodología de polinomios locales obtenemos diferentes ajustes según un abanico de amplitudes de intervalo, estimando los parámetros por medio de mínimos cuadrados. La Gráfica 18 presenta estas curvas, mientras que la Gráfica 19 exhibe el mejor ajuste, procurando obtener la curva más suave.
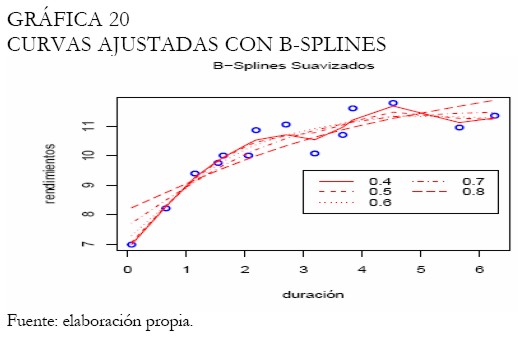
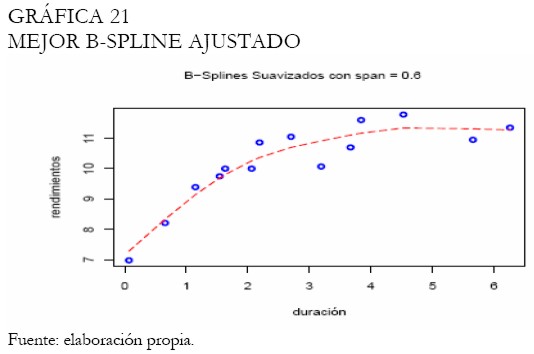
Diferentes amplitudes de intervalo son examinadas en la estimación de las tasas con B-splines, obteniendo consecuentemente los ajustes presentados en la Gráfica 20. Adicionalmente, la Gráfica 21 exhibe el mejor ajuste bajo la validación cruzada.
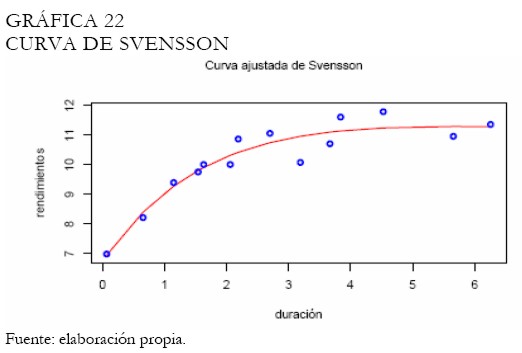
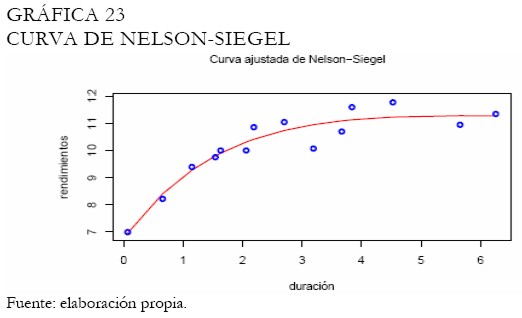
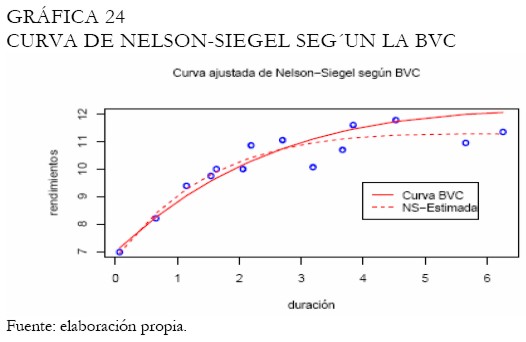
La curva estimada de Svensson se presenta en la Gráfica 22. Note que el trazo de la curva es suave en forma parecida a la presentada por la curva de Nelson-Siegel (Gráfica 23). En este caso, el ajuste de cada curva es semejante, mostrando la capacidad de la curva de Svensson para asumir una estructura semejante a la mostrada por Nelson-Siegel. Aunque la BVC tiene criterios para la selección de la muestra a ser utilizada en el proceso de estimación de los parámetros de la curva de Nelson-Siegel, este hecho puede hacer que los resultados difieran, tal y como puede observarse en la Gráfica 24.
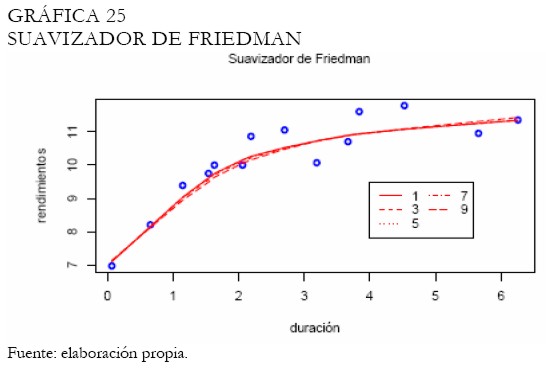
El suavizador de Friedman es evaluado sobre diferentes niveles de suavizamiento, sin embargo, los ajustes exhibidos no son realmente satisfactorios en la mitad de la curva, aunque sí en los extremos (Gráfica 25).
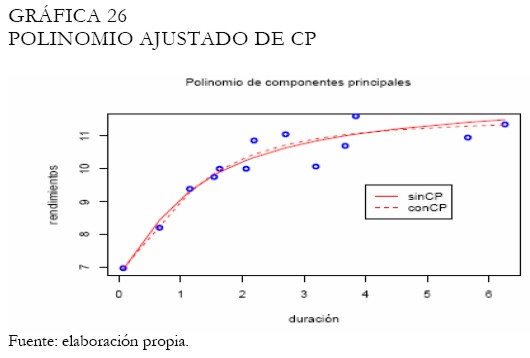
El ajuste con polinomios, basado en componentes principales se presenta en la Gráfica 26. Note como la curva bajo componentes principales ajusta satisfactoriamente los extremos de la curva en comparación con la curva polinomial tradicional.
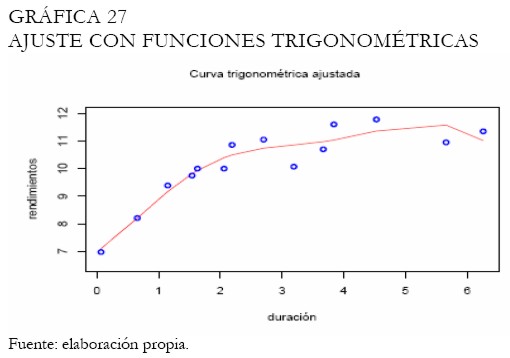
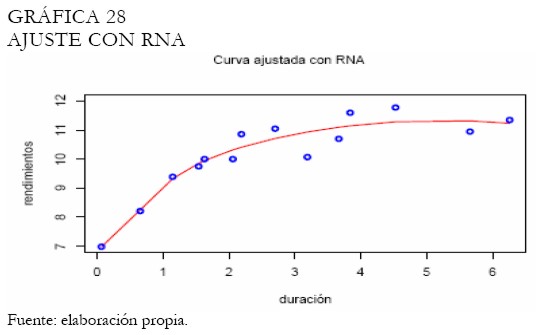
En el caso del modelo trigonométrico, el ajuste es presentado en la Gráfica 27. Puede observarse que el ajuste para las tasas de los papeles de largo plazo no es muy suave. Las redes neuronales por su lado exhiben el ajuste en la Gráfica 28, mostrándose suave. Una capa con 4 neuronas fue suficiente para captar la dinámica de los rendimientos.
En forma semejante al análisis anterior, se evalúa la bondad de ajuste de cada modelo para determinar el mejor entre ellos. El Cuadro 2 presenta los resultados ordenados según el MSE. Aunque la tabla sólo muestra tres decimales, el proceso de ordenamiento utiliza todos. Note que, los tres mejores métodos son los polinomios locales, las redes neuronales y la curva de Svensson, respectivamente. Considerando los mejores modelos según el MAPE, tenemos las redes neuronales, los polinomios locales y la curva de Svensson, respectivamente. Igualmente, es importante resaltar que las RNA registraron el menor MAPE comparado con los otros métodos.
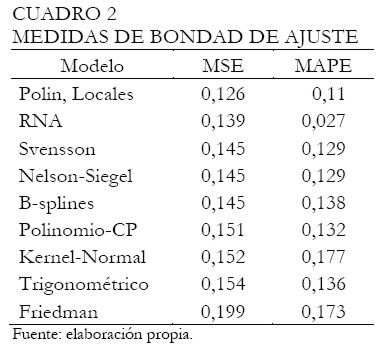 |
Estimación de los modelos paramétricos y no paramétricos sobre las tasas de los bonos del tesoro de Estados Unidos
El mercado de bonos norteamericano se caracteriza por su amplio desarrollo y liquidez, haciendo de este un marco interesante para el estudio de las curvas de rendimientos, debido a las posibles formas que ha experimentado esta curva en diferentes contextos económicos y períodos de tiempo.
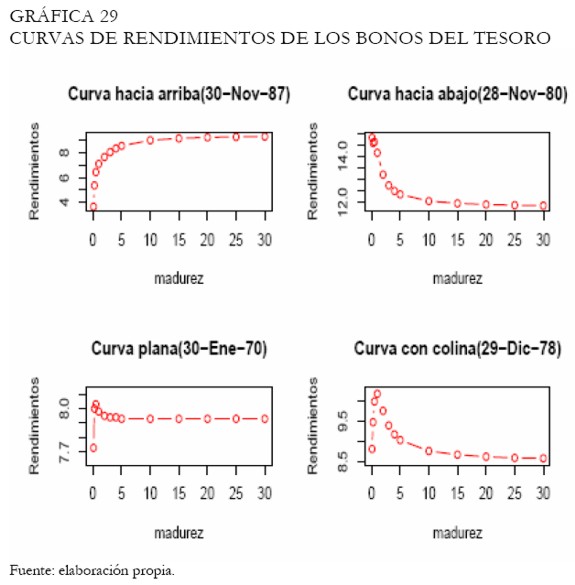
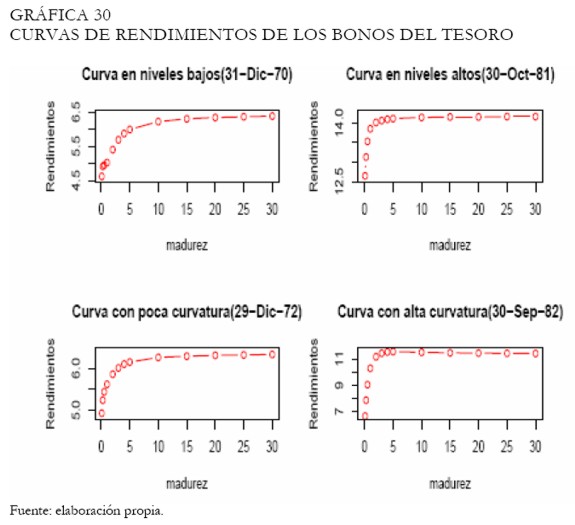
Las varias formas que pueden asumir las curvas de rendimientos fueron estimadas con cada una de las metodologías discutidas en este artículo, con el fin de evaluar su desempeño. Una base de datos con las tasas de rendimientos de los bonos del tesoro con madurez a 1, 3, 6 meses y 1, 2, 3, 4, 5, 10, 15, 20, 25 y 30 años fue utilizada8; los datos cubren el período entre enero de 1970 y enero del 2002; no obstante, fueron seleccionados ocho fechas donde se observaron las posibles formas que puede asumir la curva de rendimientos (Nelson y Siegel 1987). Las Gráficas 29 y 30 exhiben las fechas y posibles formas atribuibles (ver Anexo 2).
Los resultados son presentados como un ranking de los modelos, según su desempeño al ajustar las tasas de los bonos por tipo de curva. El predictor que se utiliza en este caso son los días al vencimiento anualizados, puesto que la base de datos no proporciona más información relativa a los bonos que permita calcular la duración modificada. Para identificar cada tipo de curva bajo análisis, se emplea la siguiente convención alfanumérica (ver el Anexo 2):
- c1: curva convexa o hacia arriba
- c2: curva cóncava o hacia abajo
- c3: curva plana
- c4: curva con colina
- c5: curva en niveles bajos
- c6: curva en niveles altos
- c7: curva con poca curvatura
- c8: curva con alta curvatura
El predictor (años al vencimiento) no resultó eficiente en el ajuste de las tasas a través de los polinomios trigonométricos, así que fue considerada una modificación del modelo, buscando mejorar el ajuste de la curva (el modelo es conocido como la transformada discreta de Fourier):
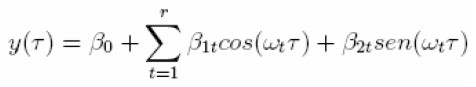 |
donde ωt, t=1, 2, ... , r (r << N ) son periodicidades ocultas obtenidas del periodograma, las cuales pueden ayudar a lograr un mejor ajuste de las tasas (Hamilton 1994, Peña, Tiao y Tsay 2001). En general, se buscó estimar el mínimo número de parámetros del conjunto [ Β 1t ] r t = 1 , debido al reducido número de observaciones.
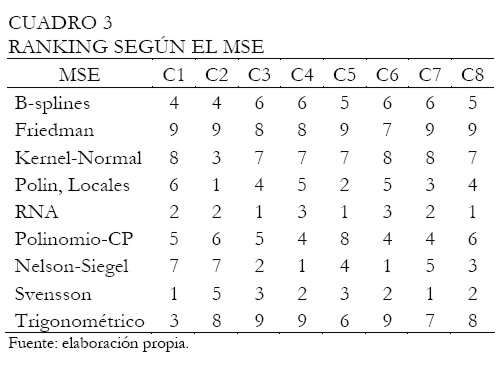
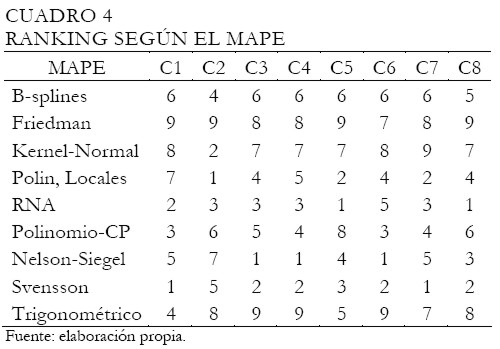
Los Cuadros 3 y 4 presentan los resultados del ranking según la bondad de ajuste de cada modelo por tipo de curva (c1 a c8), utilizando el cuadrado medio del error (MSE) y el error porcentual absoluto medio (MAPE), respectivamente. En el ranking, 1 representa el mejor modelo en tanto que 9 el peor según la medida de ajuste.
 |
 |
A partir del Cuadro 3 podemos observar en negrilla los tres primeros modelos con el mejor ajuste de las tasas, según el tipo de curva. Del conjunto de modelos no paramétricos considerados, los más destacados fueron las redes neuronales, manteniéndose siempre entre los tres primeros lugares, seguido por los polinomios locales, desempeñándose satisfactoriamente en el ajuste de las curvas c2, c5 y c7. Sobre la familia de modelos paramétricos, la curva de Svensson y Nelson-Siegel son las que tienen mejores bondad de ajuste. Note que la curva de Svensson estuvo más veces entre los primeros tres puestos comparado con Nelson-Siegel; igualmente, el número de veces que una superó a otra, según el MSE, favorece a la curva de Svensson. A través del ranking obtenido según el MSE, se clasifica cada método, del mejor al peor según el ajuste: 1) RNA, 2) Svensson, 3) Nelson-Siegel, 4) polinomios locales, 5) B-Splines, 6) polinomios de CP, 7) regresión Kernel normal, 8) regresión trigonométrica y 9) suavizador de Friedman.
Como en el caso anterior, el Cuadro 4 muestra el ranking según el MAPE, donde los métodos no paramétricos de mejor desempeño fueron las redes neuronales y los polinomios locales, mientras que entre los métodos paramétricos, los mejores fueron la curva de Svensson y Nelson-Siegel, en forma semejante a lo presentado en el Cuadro 3. En resumen, según el MAPE, podemos ordenar todos los modelos estimados, dado su desempeño en el ajuste: 1)Svensson, 2)RNA, 3) Nelson-Siegel, 4) polinomios locales, 5) polinomios de CP, 6) B-Splines, 7)regresión Kernel normal, 8) regresión trigonométrica y 9) suavizador de Friedman.
CONCLUSIONES
La curva de rendimientos es una herramienta utilizada para describir las tasas de rendimientos de un conjunto de papeles, con la misma estructura crediticia, pero con diferentes períodos al vencimiento, como un medio para representar de forma aproximada, la estructura a plazos de las tasas de interés.
Su principal utilidad se da en las decisiones de política monetaria, sobre la proyección de los ciclos de expansión o contracción de la economía. Igualmente, su conocimiento es de gran interés para quienes planifican sus inversiones, tomando decisiones a partir de la valoración, negociación o cobertura sobre instrumentos financieros.
Un conjunto de metodologías existentes en la literatura estadística y econométrica fueron utilizadas para determinar empíricamente cuál se desempeñaba mejor en el ajuste de los rendimientos de los TES tasa fija en Colombia. Aunque algunas técnicas como la Nelson-Siegel y los Bsplines son ampliamente utilizados y se tienen referencias en documentos de investigación del Banco de la República, nunca antes se había considerado una gama tan amplia de modelos econométricos, tanto de actualidad como de buen desempeño estadístico.
En el caso colombiano, dos períodos durante los cuales se observaron los niveles más altos y bajos en los precios de los TES tasa fija durante el 2006 fueron analizados; los resultados evidenciaron que los métodos de polinomios locales, redes neuronales, B-splines y Svensson se desempeñaron satisfactoriamente en el ajuste de las tasas de los TES tasa fija en Colombia, en los dos casos. Se destaca que el modelo de Nelson-Siegel no se comportó satisfactoriamente bajo el primer análisis y consiguió equiparar al modelo de Svensson en el segundo, razón por la cual se considera este último como de mejor desempeño, en comparación con el Nelson-Siegel. Este resultado es coherente con los comentarios de Svensson con respecto al desempeño de su modelo (Svensson 1994).
Con respecto a los B-splines, el primer análisis exhibió un mejor desempeño con relación a la curva de Nelson-Siegel, según las medidas de bondad de ajuste. Sin embargo, en el segundo caso, se tornaron equiparables según el MSE, mientras que bajo el MAPE, el método de Nelson-Siegel superó a los B-splines.
Las redes neuronales siguen siendo una herramienta poderosa debido a su capacidad para captar no linealidades, no siendo ajena en este análisis y demostrando su superioridad en MAPE sobre todos los modelos competidores. Bajo el MSE, este método fue rebasado, únicamente, por los polinomios locales (en los dos análisis) y los B-splines (en el primer análisis).
Las metodologías fueron nuevamente evaluadas en el contexto de los bonos de los Estados Unidos, considerando las posibles formas que puede asumir la curva de rendimientos. En este análisis fueron evidentes la capacidad de ajuste de las redes neuronales y las curvas de Svensson y de Nelson-Siegel conforme al MSE y MAPE; no obstante, modelos como los polinomios locales, los B-splines y la propuesta de polinomios con componentes principales resultaron satisfactorias, aunque en menor medida que las tres mencionadas inicialmente. Adicionalmente, como en el análisis efectuado en el contexto colombiano, se resalta las ventajas de ajustar con la curva de Svensson en comparación con la curva de Nelson-Siegel.
Finalmente, el objetivo primordial fue evaluar el desempeño y la robustez de los diferentes modelos competidores, ante las variadas formas que pueden llegar a asumir las curvas de rendimientos. Esto sin desmeritar ningún modelo en especial, haciendo notar que cada modelo tiene sus propias características, que según las circunstancias, pueden hacer que su desempeño sea mejor o peor comparado con otras técnicas, sin manifestar de ninguna manera que un modelo u otro, sea realmente ineficiente. En otras palabras, según el problema y conocimiento que se posea sobre las propiedades del modelo a utilizar, es posible llegar a describir satisfactoriamente, de manera aproximada, la estructura a plazos de las tasas de interés.
FIGURAS DEL ANÁLISIS DE LOS TES TASA FIJA DEL 30 DE MARZO DE 2006
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
GRÁFICAS DEL ANÁLISIS DE LOS TES TASA FIJA DEL 29 DE JUNIO DE 2006 Y LAS TASAS DE LOS BONOS DEL TESORO DE ESTADOS UNIDOS
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
NOTAS AL PIE
1 Ver Fan y Gijbels (1996) para una descripción detallada de estos procedimientos.
2 En el contexto colombiano, los datos fueron obtenidos a través del sistema Bloomberg y para Estados Unidos a través de la página web http://www.spreadsheetmodeling.com.
3 La duración modificada (DM) de McCaulay mide la sensibilidad del precio de un bono a los movimientos de la tasa de interés. Se calcula como DM=[D/(1+(y/n))] donde D es la duración, y el rendimiento al vencimiento y n el número de períodos por descontar anualizados.
4 Una descripción más detallada sobre la familia de curvas de Nelson-Siegel y splines suavizados puede verse en Julio et al. (2002), Melo y Vásquez (2002) y Arango et al. (2002).
5 Lenguaje de programación de acceso libre disponible en www.r-project.org. (Ver Venables y Ripley 2002).
6 Los programas pueden ser obtenidos directamente con el autor.
7 El PCE es un indicador líder que mide la tasa de inflación experimentada por los consumidores; es semejante al IPC, no obstante, es medido sobre bienes y servicios de consumo personal. Es el indicador de inflación preferido por la Reserva Federal.
8 La base de datos fue obtenida de la página web (http://www.spreadsheetmodeling.com)
REFERENCIAS BIBLIOGRÁFICAS
1. Abramovich, F. y Steinberg, D. (1996). "Improved Inference in Nonparametric Regression using Lk Smoothing Splines". Journal of Statistical Planning, 49: 327-341. [ Links ]
2. Arango, L. E.; Melo, L. F. y Vásquez, D. (2002). "Estimación de la Estructura a plazo de las tasas de Interés en Colombia". Borradores de Economía 196. Bogotá: Subgerencia de estudios económicos, Banco de la República de Colombia. [ Links ]
3. Bank for International Settlements - BIS (2005). "Zero-Cupon Yield Curves: Technical Documentation". Technical report 25. Basel: Bank of International Settlements, Monetary and Economic Department. [ Links ]
4. Bolsa de Valores de Colombia - BVC (2002). Métodos de Estimación de la Curva Cero Cupón para Títulos TES. Bogotá: Dirección de Investigación y Desarrollo. [ Links ]
5. Cámaro, Á.; Casas, A. y Jiménez, E. (2006). "Movimientos de la Curva de Rendimientos de TES Tasa Fija en Colombia", Innovar 15(26): 122-133. [ Links ]
6. Estrella, A. y Hardouvelis, G. A. (1989). "The Term Structure as a Predictor of Real Economic Activity", Research Paper 8907. New York: Federal Reserve Bank of New York. [ Links ]
7. Fan, J. y Gijbels, I. (1996). Local Polynomial Modelling and Its Applications. New York: Chapman and Hall. [ Links ]
8. Friedman, J. H. (1984). "A Variable Span Smoother", Technical report 5. Standford: Standford University - Departament of Statistics. [ Links ]
9. Hamilton, J. D. (1994). Time Series Analysis. Princeton: Princeton University Press. [ Links ]
10. Haykin, S. (1994). Neural Networks. New York: McMillan College Publishing Company. [ Links ]
11. Hunt, B. (1995). "Modelling the Yields on Australian Coupon Paying Bonds", Technical report 9. Sydney: University of Technology Sydney - School of Finance and Economics. [ Links ]
12. Hunt, B. y Terry, C. (1998). "Zero-Coupon Yield Curve Estimation: A Principal Component-Polynomial Approach", Technical report 81. Sydney: University of Technology Sydney - School of Finance and Economics. [ Links ]
13. Isasi, P. y Galván, I. (2004). Redes neuronales artificiales: un enfoque práctico. Madrid: Pearson-Prentice Hall. [ Links ]
14. Julio, J.; Mera, S. y Revéiz, A. (2002). "La Curva Spot (cero cupón), estimación con Splines cúbicos suavizados, usos y ejemplos", Borradores de Economía 213. Bogotá: Subgerencia de estudios económicos, Banco de la República de Colombia. [ Links ]
15. Kaastra, I. y Boyd, M. (1996). "Design a Neural Network for Forecasting Financial and Economic Time Series". Neurocomputing 10: 215-236. [ Links ]
16. McCulloch, J. H. (1971). "Measuring the Term Structure of Interest Rates". Journal of Business, 44: 19-31. [ Links ]
17. Melo, L. F. y Vásquez, D. (2002). "Estimación de la estructura a plazo de las tasas de interés en Colombia por Medio del Método de Funciones B-Splines Cúbicas", Borradores de Economía 210. Bogotá: Subgerencia de estudios económicos, Banco de la República de Colombia. [ Links ]
18. Nelson, C. y Siegel, A. (1987). "Parsimonius Modeling of Yield Curves". Journal of Business, 60: 473-489. [ Links ]
19. Nocedal, J. y Wright, S. (1999). Numerical Optimization. New York: Springer-Verlag. [ Links ]
20. Peña, D.; Tiao, G. y Tsay, R. (2001). A Course in Time Series Analysis. New York: John Wiley and Sons. [ Links ]
21. Sharda, R. (1994). "Neural networks for the MS/OR analyst: An application bibliography". Interfaces, 24(2): 116-130. [ Links ]
22. Suykens, J.; Vandewalle, J. y Moor, B. D. (1996). Artificial Neural Networks for Modelling and Control of Nonlinear Systems. Boston: Kluwer Academic Publishers. [ Links ]
23. Svensson, L. (1994). "Estimating and Interpreting Forward Interest Rates: Sweden 1992-1994", NBER Working Papers, 4871. Estocolmo: National Bureau of Economic Research. [ Links ]
24. Venables, W. y Ripley, B. D. (2002). Modern Applied Statistics with S, 4th ed. New York: Springer-Verlag. [ Links ]
25. Zhang, G.; Patuwo, B. y Hu, Y. (1998). "Forecasting with Artificial Neural Networks: The State of Art", International Journal of Forecasting, 14: 35-62. [ Links ]