MODELOS ARCH, GARCH Y EGARCH: APLICACIONES A SERIES FINANCIERAS

Marta Casas Monsegny*

Edilberto Cepeda Cuervo

* Marta Cecilia Casas es estudiante de Maestría en Estadística y docente del Departamento de Matemáticas de la Universidad de los Andes (Bogotá, Colombia). E-mail: mcasas@uniandes.edu.co.

Edilberto Cepeda es Doctor y Magíster en Matemáticas; actualmente se desempeña como profesor asociado del departamento de Estadística de la Universidad Nacional de Colombia (Bogotá, Colombia) y como Coordinador del grupo de investigación Inferencia Bayesiana. E-mail: ecepedac@unal.edu.co.

Este artículo fue recibido el 2 de octubre de 2007 y su publicación aprobada el 6 de febrero de 2008.

Resumen

En este artículo se incluye una descripción de los modelos ARCH, GARCH y EGARCH, y de los procesos de estimación de sus parámetros usando máxima verosimilitud. Se propone un modelo alternativo para el análisis de series financieras y se estudian las series de precios y de retornos de las acciones de Gillette. La selección de modelos usando los criterios AIC y BIC permite concluir que, de los modelos considerados el GARCH(1,2) es el que mejor explica el comportamiento de los precios de las acciones y el EGARCH(2,1) es el que mejor explica la serie de los retornos.

Palabras clave: modelos ARCH, GARCH y EGARCH, predicción. JEL: C10, C19, C32, G10.

Abstract

This article includes a description of the ARCH, GARCH, and EGARCH models and the estimation of their parameters using maximum likelihood. An alternative model is proposed for the analysis of financial series and used to study price and returns series for Gillette stock. The choice of models using AIC and BIC criteria lead us to conclude that, of the models considered, GARCH (1,2) best explains the performance of stock prices and EGARCH (2,1) best explains the returns series.

Key words: ARCH, GARCH, and EGARCH models, prediction. JEL: C10, C19, C32, G10.

Résumé

Dans cet article on présente une description des modèles ARCH, GARCH et EGARCH, et des processus d´estimation de leurs paramètres en utilisant la méthode d´estimation par maximum de vraisemblance. On propose un modèle alternatif pour l´analyse de séries financières et on étudie les séries de prix et de retours des titres en bourse de Gillette. La sélection de modèles, en utilisant les critères AIC et BIC, permet de conclure que, parmi les modèles considérés, le GARCH (1,2) c´est celui qui explique le mieux le comportement des prix des titres et l´EGARCH (2,1) est celui qui explique le mieux la série de retours.

Mot clés: modèles ARCH, GARCH et EGARCH, prévisions financières. JEL : C10, C19, C32, G10.

La volatilidad es una característica inherente a las series de tiempo financieras. En general, no es constante y en consecuencia los modelos de series de tiempo tradicionales que suponen varianza homocedástica, no son adecuados para modelar series de tiempo financieras. Engle (1982) introduce una nueva clase de procesos estocásticos llamados modelos ARCH, en los cuales la varianza condicionada a la información pasada no es constante, y depende del cuadrado de las innovaciones pasadas. Bollerslev (1986) generaliza los modelos ARCH al proponer los modelos GARCH en los cuales la varianza condicional depende no solo de los cuadrados de las perturbaciones, como en Engle, sino además, de las varianzas condicionales de períodos anteriores. En 1991, Nelson presenta los modelos EGARCH, en los cuales formula para la varianza condicional un modelo que no se comporta de manera simétrica para perturbaciones positivas y negativas, como sucede en los modelos GARCH; expresando otro rasgo de la volatilidad: su comportamiento asimétrico frente a las alzas y bajas de los precios de un activo financiero. Un elevado número de trabajos sobre modelos de volatilidad se han publicado en las últimas décadas. Ver Poon y Granger (2003), Hansen y Lunde (2006) y Novales y Gracia (1993).

Este artículo está dividido en seis secciones. En la primera se define el retorno de un activo financiero. En la segunda sección se discuten algunas características de la volatilidad. En la tercera parte se define el modelo ARCH en regresión propuesto por Engle (1982), se muestra cómo se estiman sus parámetros utilizando el algoritmo de Fisher-Scoring y se presenta la generalización de un ejemplo desarrollado por Engle (1982). En el cuarto apartado se definen los modelos GARCH introducidos por Bollerslev (1986) y la forma cómo se estiman sus parámetros. En la quinta sección se definen los modelos EGARCH propuestos por Nelson (1991) y sus características. En el apartado 6, se estudian las series de los precios y de los retornos de las acciones de la compañía Gillette, y se proponen varios modelos para las dos series. La selección del modelo se hace utilizando el criterio de información de Akaike AIC, el criterio de información bayesiana BIC cuando los modelos son anidados y la suma de cuadrados de los residuales para los modelos no anidados.

RETORNO DE UN ACTIVO FINANCIERO

Según Fabozzi et al. (1996):

un activo, en términos generales, es cualquier posesión que tiene valor en un intercambio. Los activos pueden clasificarse como tangibles o intangibles. Un activo tangible es aquel cuyo valor depende de sus propias características; por ejemplo, un edificio, maquinaria, terrenos, etc. Un activo intangible, por el contrario, representa obligaciones legales sobre algún beneficio futuro.

Los activos financieros son activos intangibles, dado que su valor o beneficio es una obligación de dinero a futuro. Por ejemplo, un bono es una obligación financiera contraída por el inversionista; o puede ser considerado como un certificado de deuda, es decir, una promesa de pago futura documentada en un papel y que determina monto, plazo, moneda y secuencia de pagos. Cuando un inversionista compra un bono, está prestando su dinero a un gobierno, a un ente territorial, a una agencia del Estado, a una corporación o a una compañía. En contraprestación a este préstamo, el emisor acuerda pagar al inversionista unos intereses durante la vida del bono, hasta que éste llegue a su vencimiento, reembolsando la cantidad prestada. Otro ejemplo de un activo financiero son las acciones; cada una de las cuales da derecho al inversionista a recibir dividendos, distribuidos por la compañía que emite la acción; estos pagos estarán relacionados con las ganancias de la empresa. A diferencia de los bonos, el poseedor de una acción común no tiene certeza de la cantidad, ni del momento en que se paguen los dividendos.

Sea P_t , t = 1, 2, . . . , el precio de un activo en el tiempo t. Asumiendo que el activo no paga dividendos, su tenencia por un período de tiempo, desde t - 1 hasta t, producirá un retorno simple definido como

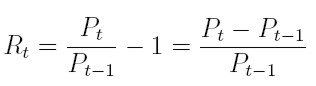[1]

Sobre este período de tiempo se define el log-retornos (r_t ), mediante la expresión:

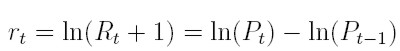[2]

Obsérvese que la serie de los log-retornos, que llamaremos la serie de los retornos, no tiene unidades, es estable en la media y facilita el cálculo de un retorno compuesto k períodos desde el tiempo t - k hasta el tiempo t (Tsay 2002). Así:

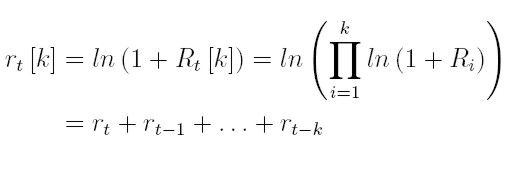[3]

CARACTERÍSTICAS DE LA VOLATILIDAD

Se define la volatilidad como la varianza condicional de la serie subyacente. En el caso de las series de tiempo financieras, se modela la volatilidad de los retornos. Es de anotar que, aunque la serie sea estacionaria y tenga, por tanto, varianza constante, puede presentar oscilaciones a corto plazo que es lo que recoge la varianza condicional para el estudio de la volatilidad cuyo conocimiento es de interés, en particular, para hacer predicciones a corto plazo. Debido a que la volatilidad varía en el tiempo, los modelos clásicos de series de tiempo no son adecuados para modelarla, puesto que uno de sus supuestos es que la varianza es constante.

La volatilidad no es observable directamente, para un día, por ejemplo, se tiene una única observación. En las series financieras se presenta períodos largos de alta volatilidad seguidos por períodos de baja volatilidad, lo que indica la presencia de heterocedasticidad. Son más interesantes las medias y las varianzas condicionadas a la información pasada (pronósticos a corto plazo) que las medias y varianzas no condicionadas (pronósticos a largo plazo).

Un buen modelo para la volatilidad debe tener la capacidad de pronosticarla; por tanto, debe modelar sus características. En general, esta clase de modelos es utilizada para hacer proyecciones y estimaciones, por ejemplo, pronosticar el valor absoluto de la magnitud de los retornos de los precios de un activo, estimar cuantiles o incluso toda la función de densidad de probabilidad de los retornos. Estos pronósticos y estimaciones son utilizados en diversas actividades financieras: manejo de riesgo, selección de portafolio, posiciones cortas y largas en la tenencia de un activo, entre otras.

Un buen modelo para la volatilidad de los retornos debe reflejar las siguientes características (Engle y Patton 2001):

• Aglomeración de la volatilidad. La volatilidad tiene tendencia a aparecer agrupada por períodos, es decir, que la volatilidad puede ser alta durante un período y baja durante otro. A grandes cambios en la volatilidad siguen cambios grandes; a peque˜nos cambios, siguen peque˜nos cambios de volatilidad. Este comportamiento ha sido reportado en numerosos estudios, como Baillie et al. (1996), Chou (1988) y Schwert (1989). A la aglomeración de la volatilidad se debe el hecho de que los choques de hoy influyan en el valor esperado de la volatilidad varios períodos en el futuro. La Gráfica 1 muestra la variabilidad de la varianza de los retornos de las acciones de Gillette entre enero 4 de 1999 y mayo 13 de 2003, y muestra evidencia de que la volatilidad varía en el tiempo.

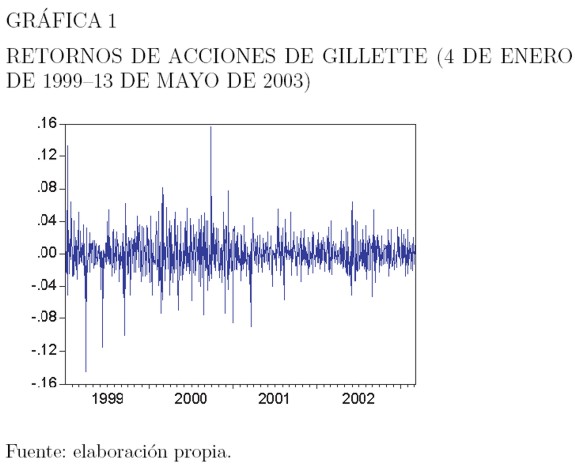• Reversión a la media. La aglomeración de la volatilidad implica que a un período de alta volatilidad, eventualmente, seguirá otro de volatilidad normal, y a un período de baja volatilidad seguirá uno de volatilidad más alta. La volatilidad tiende a revertirse a la media, en otros términos, existe un nivel normal de volatilidad al cual ésta retorna eventualmente. Los pronósticos a largo plazo convergerán todos al nivel normal de la volatilidad, sin importar cuando fueron hechos.
• La volatilidad es asimétrica. La volatilidad se comporta diferente frente a innovaciones positivas y negativas. No reacciona de la misma manera frente a una gran alza en el precio de un activo que frente a una caída en su precio. Varios de los modelos imponen el supuesto de que la varianza condicional es afectada simétricamente por las innovaciones positivas y negativas, por ejemplo, en un modelo ARCH(p), la varianza depende del cuadrado de las innovaciones retardadas, ignorando este efecto de asimetría. Esta asimetría recibe el nombre de efecto de apalancamiento y ha sido modelada entre otros, por los EGARCH. Evidencia de este efecto ha sido encontrada por Nelson (1991), Glosten et al. (1993), Engle y Ng (1993), entre otros.
• Influencia de variables exógenas. Evidentemente, nadie considera que los precios de los activos financieros evolucionan independientemente de los mercados alrededor de éstos y, por ello, cabría esperar que existan variables que contengan información relevante para la volatilidad de la serie. Esto ha sido tratado por Bollerslev y Melvin (1994), Engle, Mezrich (1996), Engle, Ito y Lin (1990), entre otros, encontrando que las variables exógenas pueden influir en la volatilidad.

Además, es posible que eventos determinísticos repercutan, también, en la volatilidad de la serie. Ejemplos de tales eventos pueden ser los informes periódicos de una compa ñía, las nuevas políticas macroeconómicas. Por ejemplo Andersen y Bollerslev (1998) hallaron que la volatilidad de la tasa de cambio del dólar, frente al marco alemán, aumentaba, notablemente, en la época en la que se publicaba la nueva información macroeconómica de Estados Unidos, como el Reporte de Empleo o el Índice del Precio de Producción.

• Distribución de probabilidad. La distribución de probabilidad de los retornos tiene colas pesadas y, en general, exceso de curtosis.

MODELOS ARCH

Engle (1982) propuso el modelo ARCH, que significa modelo auto regresivo condicionalmente heterocedástico, el cual hace parte de la familia de modelos adecuados para modelar la volatilidad de una serie.

Modelo ARCH(p) en regresión

Si la variable aleatoria {y_t}_t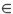I (donde I es un conjunto discreto de índices), es muestreada de la función de densidad condicional f( y_t | ψ_{t -1} ), el pronóstico del valor actual de la variable condicionado a la información pasada ψ_{t -1}es µ_t = E(y_t | ψ_{t -1}). La media puede modelarse, por ejemplo, a través del modelo de regresión µ_t = x_t β, donde x_t = (1, x_{t 1}, . . . , x_tk ) es el vector de observaciones de las variables independientes y β´ = ( β₀, β₁, . . . , β_k) es un vector de parámetros desconocidos. La varianza condicional, Var(y_t | ψ_{t -1}), depende de la información pasada y esta dependencia puede modelarse mediante una función h_t = h ( e_{t - 1}, e_{t - 2}, ..., e_{t - p}, α ), la cual se tiene en cuenta que la varianza es positiva y donde α´ = (α₀, α₁, . . . , α_p ) es un vector de parámetros desconocidos. En este modelo, e_t = y_t - x_t β para t 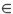I y la información ψ_{t -1}es la sigma álgebra generada por { e_{t - 1}, e_{t - 2}, ..., }

Un proceso {y_t}_t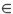I obedece al modelo en regresión auto regresivo condicionalmente heterocedástico de orden p, ARCH(p) (Engle 1982), si:

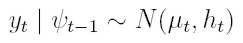[4]

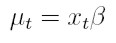[5]

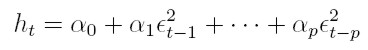[6]

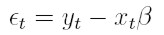[7]

con α₀ > α_i ≥ 0, i = 1, . . . , p

De los supuestos del modelo se deduce que e_t | ψ_{t -1} N( 0, h_t) y si el proceso y_t | ψ_{t -1}tiene media µ_t = 0, e_t = y_t. En este caso, el modelo puede expresarse como:

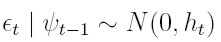[8]

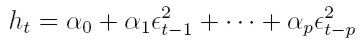[9]

que es el modelo ARCH(p) propuesto, inicialmente, por Engle. Además, la varianza h_t puede modelarse mediante un proceso auto regresivo de orden p. AR(p) en las variables u_t = e²_t. De igual forma, las esperanzas y varianzas no condicionales para el modelo definido por (8) y (9) son:

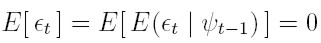[10]

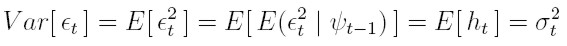[11]

y si la varianza condicional h_t está dada por la ecuación (9), al sustituirla en la ecuación Var [ e_t ] = E [ h_t ] obtenemos:

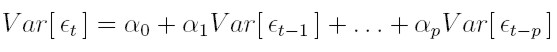[12]

y dado que el proceso { e_t } es estacionario, Var [ e_t ] = Var [ e_t - k ] para todo k y, despejando, la varianza no condicional está dada por:

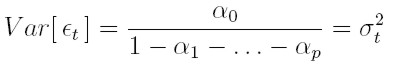[13]

Debido a este resultado se tiene, en este caso, una restricción más para los parámetros de la varianza: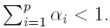

Función de verosimilitud

Suponga que {y_t}_t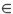I se genera por medio de un proceso ARCH(p) en regresión como el definido por las ecuaciones (4) a (7). Entonces, la función de verosimilitud para la observación t-ésima es:

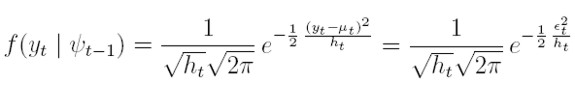[14]

y su logaritmo es, salvo constantes:

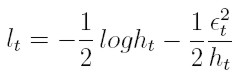[15]

Así, el logaritmo de la función de verosimilitud, denotado l, para T observaciones es:

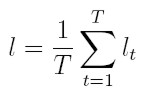[16]

La función l_t puede ser maximizada respecto a los vectores de parámetros desconocidos α y β. Los estimadores máximo veros ímiles se encuentran al resolver el sistema dado por las condiciones de primer orden:

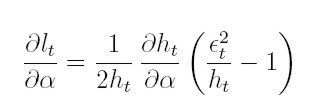[17]

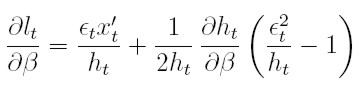[18]

Estas dos últimas ecuaciones se obtienen así: para la ecuación (17), la derivada parcial de l_t respecto a la componente j-ésima de α ≤ j ≤ p, es:

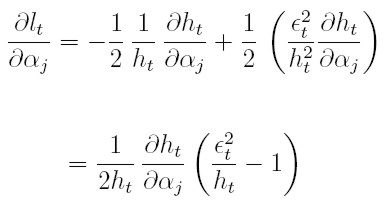[19]

Para la (18), la derivada parcial de l_t respecto a β_l, para 1 ≤ l ≤ k es:

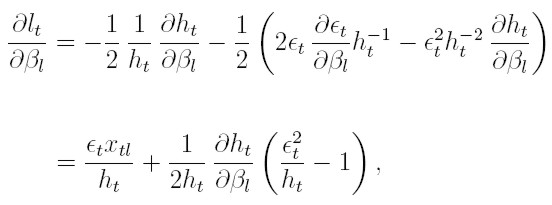[20]

puesto que 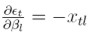, para 1 ≤ l ≤ k.

Los bloques de la matriz hessiana H serán:

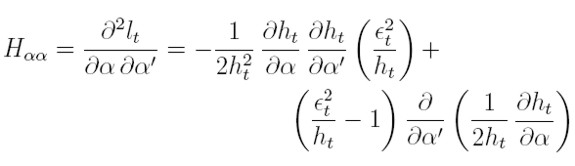[21]

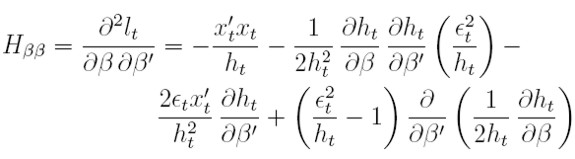[22]

[23]

Los hessianos se obtienen al derivar parcialmente las ecuaciones (17) y (18) respecto a α y β.

La matriz de información, denotada I, es:

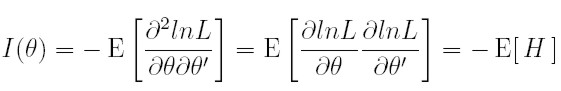[24]

donde H es la matriz hessiana y θ el vector de parámetros. Al estimar la matriz de información se hallan las varianzas estimadas de los parámetros, lo que nos permite realizar estimaciones de los parámetros por intervalos de confianza.

En el caso que se está tratando, el cálculo de la matriz de información se simplifica si se condiciona a la información pasada ψ_{t -1}y se tienen en cuenta los siguientes hechos:

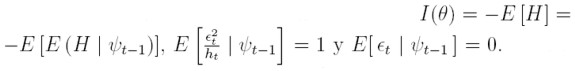
Entonces, es posible obtener obtener los bloques de la matriz de información aplicando la esperanza condicional a las ecuaciones (17), (22) y (23):

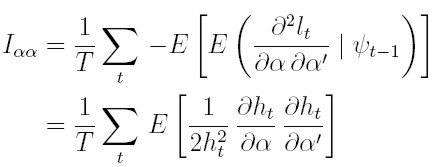[25]

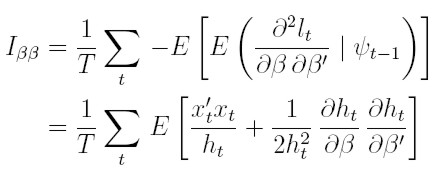[26]

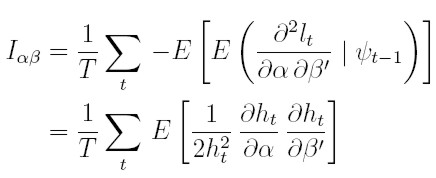[27]

Por ejemplo, para obtener el resultado (25) al calcular la esperanza condicionada a la información pasada a la ecuación (21), la esperanza del primer sumando es el resultado que muestra (25) y la del segundo sumando es cero. De manera similar se obtienen los bloques restantes de la matriz de información.

Ejemplo (Engle 1982). Se mostrará cómo es la matriz de información estimada para el modelo ARCH(p) en regresión, definido por las ecuaciones (4) a (7). Para ello, se expresará el modelo en notación vectorial: sean x_t = (1, x_t1, x_t2 . . . , x_tk), β´ = (β₀, β₁, β₂ . . . , β_k), z_t = (1, e² _{t- 1}, ...,e² _{t- p} ) y α´ = (α₀, α₁, . . . , α_p). Así, la media y la varianza del modelo pueden expresarse como:

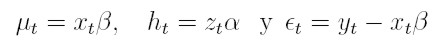Los bloques de la matriz de información están dados por:

1. Para los parámetros de la varianza:



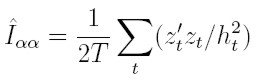
Este resultado se deriva de (25) y de que δh_t / δα_i = e² _{t- 1}, si 1 ≤ i ≤ p y δh_t / δα₀ = 1; por ello δh_t / δα = z´ y δh_t / δα´ = z_t

2. Para los parámetros de la media:



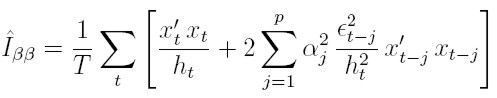
Este resultado se deriva de (26) y de



para 1 ≤ l ≤ k, de donde se tiene que 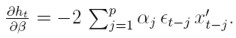. El término 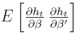puede ser estimado consistentemente por:



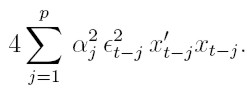
3. Si el modelo ARCH(p) es simétrico, I_αβ = 0 (Engle, 1982). En este caso, el proceso de estimación puede desarrollarse a través de un algoritmo iterativo como el indicado en la sección.

Estimación de parámetros

La estimación de los parámetros y de sus varianzas se hace mediante el algoritmo de Fisher-Scoring, si:

• θ^(k) es el vector de los valores de los parámetros en la iteración k-ésima del algoritmo.
• q^(k) es el vector q = 1/T ∑_t ( δl_t / δθ ) evaluado en θ ^(k).
• I ( θ ^(k) ) es el valor de la matriz de información I(θ) evaluada θ ^(k)

el algoritmo sería:

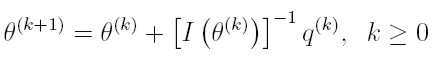Si I_{α β} = 0, podemos proponer un algoritmo iterado alternado de Fisher-Scoring para obtener las estimaciones máximo verosímiles de los vectores de parámetros α y β, como el propuesto en Aitkin (1987) o en Cepeda y Gamerman (2001) para modelos lineales con varianza variable. De esta manera, el algoritmo de Fisher-Scoring puede formularse a partir de las siguientes ecuaciones:

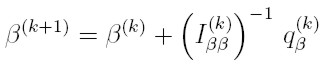[28]

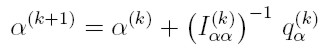[29]

donde β^(k) y α^(k), son los valores de los vectores β y α, en la iteración k-ésima del algoritmo, y ( I ^(k) _ββ ) ^-1 e ( I ^(k) _αα ) son las matrices inversas de I_αα e I_ββ evaluadas en β^(k) y α^(k), respectivamente. Por último, q^(k) _β y q^(k) _α son los vectores q_β = 1/T ∑_t ( δl_t / δβ ) y q_α = 1/T ∑_t ( δl_t / δα ) evaluados, respectivamente, en β^(k) y α^(k).

El algoritmo para obtener las estimaciones de máxima verosimilitud de los parámetros para la media y la varianza es:

1. Dar valores iniciales para β y α, β⁽⁰⁾ y α⁽⁰⁾.

2. Utilizando β^(k) y α^(k), estimar I ^(k) _ββ y q ^(k) _β.

3. Calcular β^(k+1) utilizando la ecuación (28).

4. Utilizando β^(k+1) y α^(k), estimar I ^(k) _αα y q ^(k) _α

5. Calcular α^(k+1) utilizando la ecuación (29).

6. Repita los pasos 2 a 5 hasta que se cumpla algún criterio de convergencia.

Pruebas para detectar efectos ARCH

Para detectar la presencia de efectos ARCH existen varias maneras: una, es utilizar los estadísticos tradicionales de Ljung-Box en los correlogramas de los residuos de la ecuación de la media y de los residuos al cuadrado (Tsay 2002); otra, es utilizar una prueba de multiplicadores de Lagrange LM, propuesta tanto por Engle (1982) como por Bollerslev (1986) en la que después de expresar la ecuación de la varianza condicional h_t = z_t1w como h_t = z_t1w₁ + z_t2w₂, se prueba la hipótesis nula H₀ : w₂ = 0 mostrando así, que el efecto ARCH es a lo mas como la dimensión de w₁.

MODELOS GARCH

Una clase más general de modelos, los GARCH (modelos generalizados auto regresivos condicionalmente heterocedásticos), que extiende la clase de los modelos ARCH, fue introducida por Bollerslev (1991). En éstos la estructura de la varianza condicional depende, además del cuadrado de los errores retrasados q períodos como en el modelo ARCH(q), de las varianzas condicionales retrasadas p períodos.

Modelo GARCH(p, q) en regresión

Sea {y_t}_t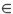I un proceso estocástico donde T es un conjunto discreto de índices. Sean

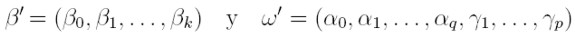vectores de parámetros para modelar la media y la varianza respectivamente, z_t = (1, e² _{t -1}, . . . , e² _{t - q}, h_{t -1}, . . . , h_{t- p}) el vector de variables para la varianza, x_t = (1, x_t1, . . . , x_tk) el vector de variables explicativas observadas en el tiempo t. En este modelo, e_t = y_t - x_t β y ψ_{t -1} es la información disponible hasta el tiempo t - 1. El modelo GARCH(p, q) en regresión Bollerslev (1991) está dado por:

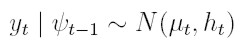[30]

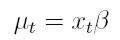[31]

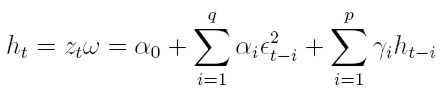[32]

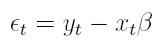[33]

donde p ≥ 0, q ≥ 0, α₀ ≥ 0, α_i ≥ 0, i = 1, . . . , q y γ_i ≥ 0 i = 1, . . . , p.

Ahora la varianza condicional depende tanto del cuadrado de los errores como de las varianzas condicionales retrasadas p períodos, como se indica en (32). Si p = 0, se tiene el proceso ARCH(q) en regresión.

Estimación de parámetros

Notaremos θ = { θ : θ = (β´ , w´)} el espacio de parámetros, un subespacio compacto de un espacio euclidiano, donde β´ = (β₀, β₁, . . . , β_k) y w´ = (α₀, α₁, . . . , α_q, γ₁, . . . , γ_p). La función de verosimilitud para una muestra de T observaciones, tiene la forma dada en la ecuación (14) del proceso ARCH(q):

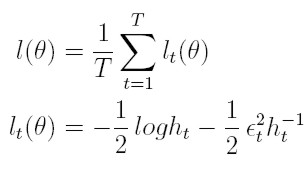Derivando l_t (θ) con respecto a los parámetros para la varianza, obtenemos, de manera semejante al proceso ARCH(q), las condiciones de primer y segundo orden para la varianza serán:

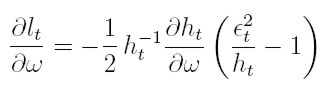[34]

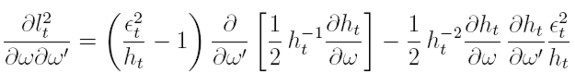[35]

donde

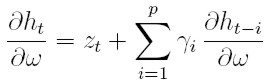[36]

Este resultado se obtiene dado que 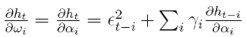para 1 ≤ i ≤ q,

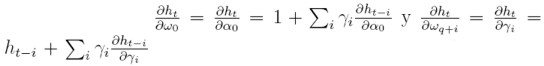para 1 ≤ i ≤ p. En el ejemplo del modelo ARCH de Engle, la derivada de la varianza respecto al vector de parámetros es igual a z_t. La única diferencia con el modelo ARCH de Engle es el término recursivo.

Si a la ecuación (35) le cambiamos el signo, dado que

como el valor de la esperanza condicionada a la información pasada del primer término del lado derecho de la ecuación (35) es cero, la matriz de información para los parámetros de la varianza está dada por:

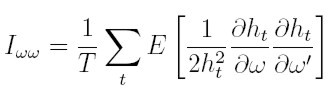I_ww es estimada consistentemente por su análogo muestral, que involucra únicamente las primeras derivadas,

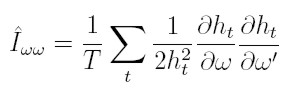Diferenciando la verosimilitud con respecto a los parámetros para la media, obtenemos las condiciones de primer y segundo orden para la media:

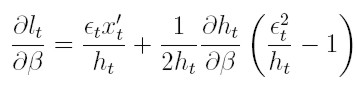[37]

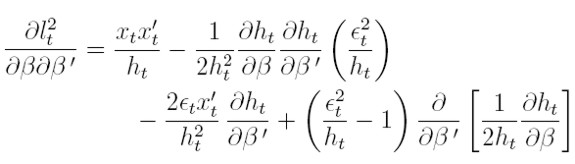[38]

donde

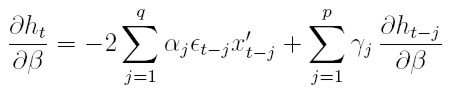[39]

Observe que, en el ejemplo 1 del modelo ARCH de Engle, la derivada de la varianza respecto a los parámetros de la media es igual al primer sumando de la ecuación (39). Se diferencian en el segundo sumando, en la inclusión de la parte recursiva.

De manera similar al caso para la varianza, a partir de la ecuación (37), se encuentra que la matriz de informacón para los parámetros de la media es:

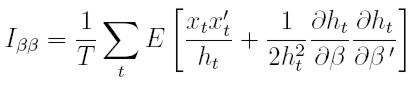que será estima consistentemente por los dos primeros términos de (37), reemplazando e²_t / h_t por su valor esperado, condicionado a la información pasada, que es 1 y estará dada por:

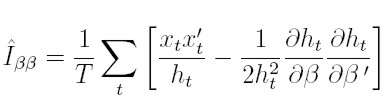Por último, de manera similar a como se hizo para el modelo ARCH(p), se tiene:

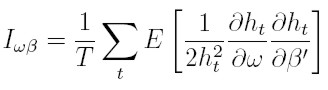Puede mostrarse que los bloques, fuera de la diagonal de la matriz de información, son nulos y la estimación de los parámetros puede hacerse en forma separada, por ejemplo, vía un algoritmo del tipo Scoring.

MODELO EGARCH

Los modelos GARCH no reflejan completamente la naturaleza de la volatilidad de algunos activos financieros. Estos modelos no tienen en cuenta un comportamiento asimétrico propio de la volatilidad de los retornos de las series financieras, que es el efecto de apalancamiento. En otras palabras, la volatilidad se comporta diferente frente a innovaciones positivas que frente a negativas. No reacciona de la misma manera frente a un alza en el precio de un activo que con respecto a una caída en el precio de éste. En los modelos GARCH, dado que la volatilidad depende del cuadrado de los errores, esta es afectada simétricamente por las innovaciones positivas y negativas. Además, los parámetros para la volatilidad tienen restricciones: deben ser no negativos.

Modelo EGARCH(p, q)

Para incluir el efecto asimétrico que tiene el cambio de los precios de un activo en su volatilidad, Nelson (1991) propone el modelo EGARCH (modelo exponencial generalizado, auto-regresivo, condicionalmente heterocedástico). Modela el efecto de asimetría al considerar una función g de las innovaciones z_t, que son variables i.i.d. de media cero, que involucra, tanto el valor de la innovación z_t como su magnitud expresada por medio de |z_t|-E (|z_t|). En términos matemáticos:

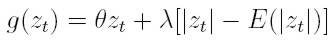donde θ y λ son números reales. El efecto de asimetría puede verse claramente al expresar la función g por casos,

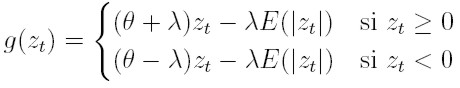Con esta definición de g, decimos que un proceso estocástico {y_t}_t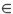I , donde T es un conjunto discreto de índices, obedece un modelo en regresión exponencial generalizado condicionalmente heterocedástico de órdenes p y q, EGARCH(p, q), si satisface:

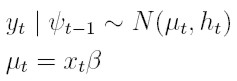[40]

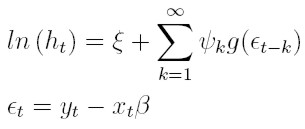[41]

donde x_t = (1, x_t1, . . . , x_tk) es el vector de observaciones de las variables explicativas, β´ = (β₀, . . . , β_k) es un vector de parámetros desconocidos, ξ es una constante y los parámetros ψ_k para la varianza satisfacen la condición ∑^∞ _{k = 1} | ψ_k | ² < ∞.

En (40), si la media es cero no se tiene el supuesto de normalidad y los errores se definen como e_t = z_th^1/2_t (donde {z_t} _t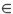I son variables i.i.d. de media cero, varianza 1 y tienen distribuci ón del error generalizado con parámetro ν), se tiene el modelo EGARCH propuesto inicialmente por Nelson (1991) y la verosimilitud para T observaciones está dada por:

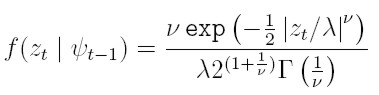donde 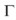( . ) es la función gama,

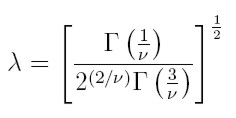ν es un parámetro positivo, y si es igual a 2, se tiene la distribuci ón normal. A partir del logaritmo de la verosimilitud para T observaciones, se obtienen, de manera semejante a los modelos anteriores, las estimaciones de los parámetros para la media y la varianza.

La ecuación (41) puede expresarse como:

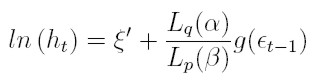[42]

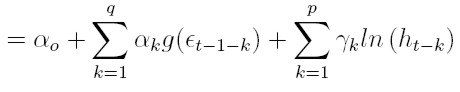[43]

donde ξ y α_o son constantes, L es el operador de retardo tal que L(g(z_t)) = g(z_{t - 1}), y L_q(α) = 1 + α₁ L + . . . + α_q L^q y L_p(β) = 1- β₁L -. . . β_pL^p son polinomios que no tienen factores comunes y sus raíces están fuera del círculo unitario. La ecuación (42) expresa el logaritmo de la varianza como un modelo ARMA en las variables u_t = g (e_t).

APLICACIÓN

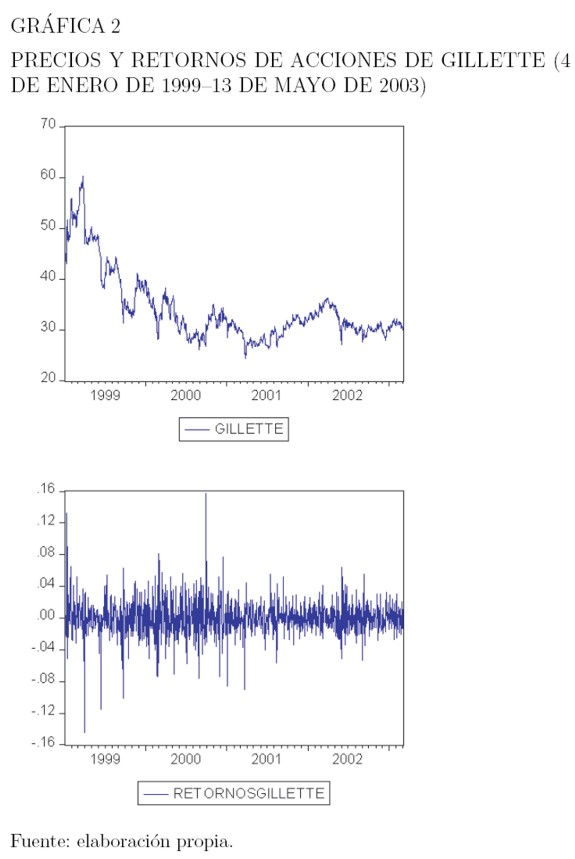
En esta sección se estudian las series de precios y retornos de las acciones de la compañía Gillette, obtenidas por medio de la compañía Bloomberg y tomados diariamente al cierre del mercado, entre enero de 1999 y mayo de 2003. Los resultados de esta aplicación fueron obtenidos utilizando el programa estadístico Eviews 5.0. La Gráfica 2, muestra el comportamiento de los precios y de los retornos de estas series, en el período referido.

La selección de los modelos se hace utilizando el criterio de información de Akaike (AIC)

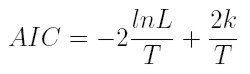y el criterio de información bayesiana (BIC)

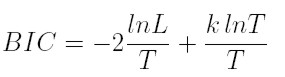donde L es la verosimilitud, T es el número de observaciones y k es el número de parámetros estimados en el modelo. Entre los modelos ARCH y GARCH, que satisfacen los supuestos de no correlación de los residuales y de los residuales al cuadrado, se escoge el de menor valor de BIC o AIC.

La comparación de los modelos EGARCH y GARCH al ser no anidados, se hace mediante la suma de cuadrados de los errores, SCE = ∑ e´ e , donde e es el vector de errores o residuales, seleccionándose el modelo de menor SCE.

Descripción de los retornos

En el Cuadro 1, se muestran algunos estadísticos de la serie de los retornos de los precios de las acciones de Gillette. La media 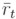de los retornos, aún cuando es negativa, es un valor muy cercano a cero; el coeficiente de sesgo es positivo y la curtosis es muy alta en comparación con la de la distribución normal, que es 3. Aparece además, el valor del estadístico de Jarque-Bera con el p-valor correspondiente a la prueba de hipótesis H₀: los retornos tienen distribución normal versus H₁: los retornos no tienen distribución normal y puede concluirse que los retornos no tienen distribución normal.

MODELO PARA LOS PRECIOS

En esta sección, se muestran algunos de los modelos que resultan del análisis de la serie de precios, entre los cuales se selecciona el modelo con el menor BIC y el menor AIC. La verificación de los supuestos de los modelos para la media y la varianza, se hace por medio de los correlogramas de las autocorrelaciones y de las autocorrelaciones parciales de los residuales (para la media), de los residuales al cuadrado (para la varianza) y del estadístico Q de Ljung-Box para la prueba de hipótesis H₀: no existe correlación serial hasta el orden k versus H₁: existe correlación serial hasta el orden k. Para los modelos ARCH y GARCH, presentados en este apartado, el estadístico Q no rechaza la hipótesis "H₀: no existe correlación serial para todo k < 36" , tanto para los residuos como para el cuadrado de los residuos, a un nivel de significancia del 1%.

Los modelos EGARCH para la serie de los precios no satisfacen los supuestos de no correlación, ya sea en los residuales o en los residuales al cuadrdo, o no se rechaza la hipótesis H₀: θ = 0 donde θ es uno de los parámetros de la varianza. En consecuencia, estos modelos, no se tienen en cuenta para modelar los precios.

Modelos ARCH

Entre los modelos ARCH, el de menor valor de AIC y BIC es el ARCH(4). Sin embargo, estos valores son similares a los obtenidos para el modelo ARCH(3), como puede observarse en el Cuadro 2.

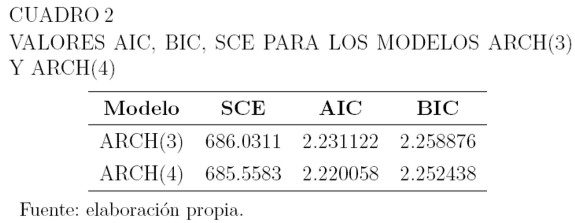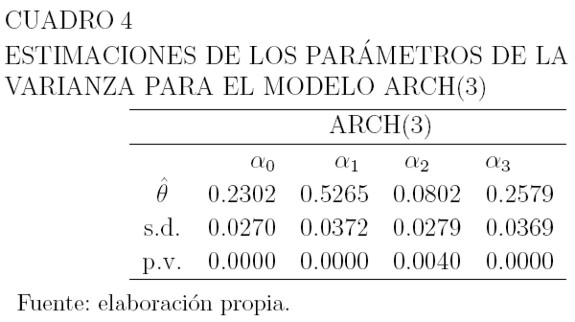
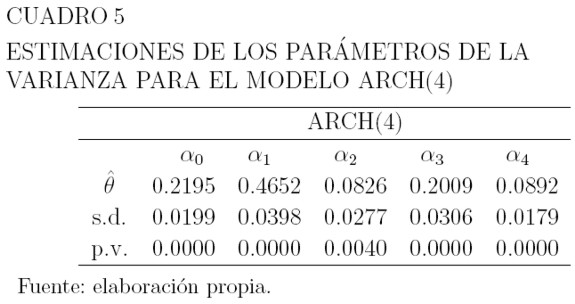
Los Cuadros 3, 4 y 5 muestran los valores estimados de los parámetros de la media y la varianza para estos modelos, sus errores estándar, y el p-valor correspondiente a las pruebas de hipótesis H₀: θ = 0 versus H₁: θ ≠ 0 para los parámetros. La hipótesis H₀, se rechaza a un nivel de significancia del 3% para los parámetros de la media y del 1% para la varianza. Para modelar la media en ambos casos, se usa como variable explicativa el precio retrasado un período: µ_t = β₀ + β_1yt-1, y las varianzas están dadas por la ecuación (6).

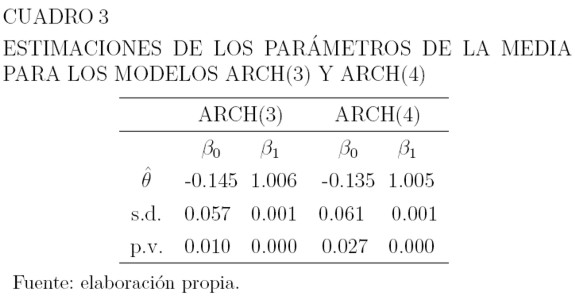Modelos GARCH

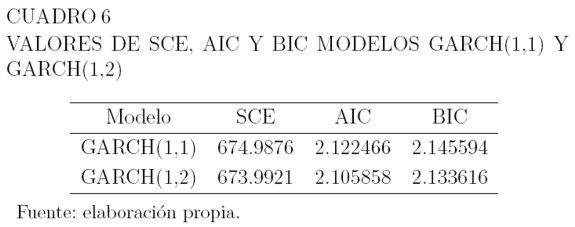
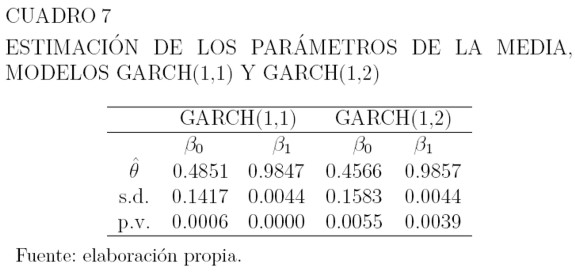
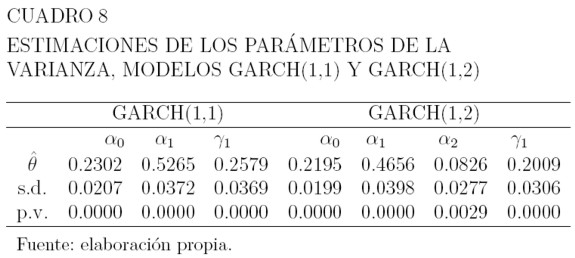
De los modelos GARCH, el que tiene menor valor en los criterios de información AIC y BIC, es el GARCH(1,2) seguido por el GARCH(1,1) como se puede ver en el Cuadro 6. Los Cuadros 7 y 8 muestran los valores estimados de los parámetros para media y varianza, las respectivas desviaciones estándar, y el pvalor correspondiente a las pruebas de hipótesis H₀ : θ = 0 versus H₁ : θ ≠ 0 para estos parámetros. La hipótesis H₀ se rechaza a un nivel de significancia del 1% para los parámetros de la media y la varianza. Las ecuaciones para la media, son como las de los modelos ARCH y la varianza se define por la ecuación (32).

Selección del modelo

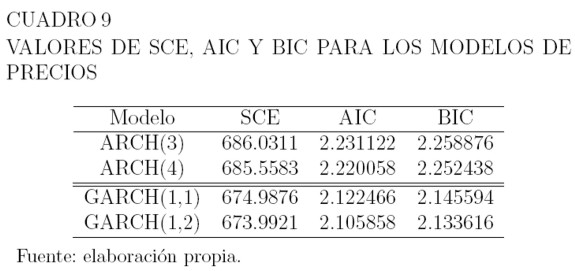
El Cuadro 9 muestra la suma de cuadrados de los errores SCE, el valor de los criterios de información de Akaike AIC y el criterio de información bayesiana BIC para los modelos ARCH(3), ARCH(4), GARCH(1,1) y GARCH(1,2). El modelo de menor valor en AIC y BIC es el GARCH(1,2) y es el de menor valor en SCE. Por ello, el modelo seleccionado para la serie de los precios es el GARCH(1,2).

Modelo para los retornos

Para la serie de los retornos de Gillette, a diferencia de las observaciones de los precios, los modelos ARCH no son convenientes para la modelación, puesto que, fallan en alguno de los supuestos. En general, no satisfacen los supuestos de no correlación, ya sea de los residuales o de los residuales al cuadrado; de los modelos, el único que cumple todos los supuestos es el ARCH(2).

Los modelos GARCH y EGARCH, en general, resultan adecuados para modelar los retornos. Los residuales y sus cuadrados satisfacen el supuestos de no autocorrelación y los parámetros de la varianza son significativos a un nivel de significancia del 5%. El Cuadro 10 muestra, para los modelos que satisfacen los supuestos, los valores de la SCE, de los criterios de información de Akaike AIC y de los criterios de información bayesiano BIC.

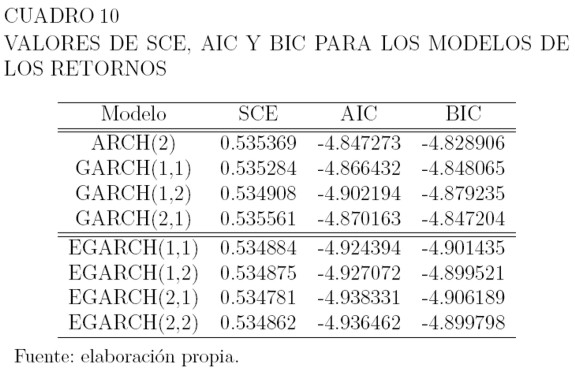Para elegir un modelo para los retornos, entre los modelos ARCH y GARCH, se selecciona uno utilizando los criterios de información AIC y BIC. De la misma manera, se elige un modelo entre los EGARCH. Finalmente, de los dos modelos anteriores se escoge uno, mediante la suma de los cuadrados de los errores.

Como puede verse en el Cuadro 10, entre los modelos ARCH y GARCH, el que tiene menor valor en AIC y BIC, es el GARCH(1,2). Entre los modelos EGARCH, el de menor valor en AIC y BIC, es el EGARCH(2,1). De los modelos GARCH(1,2) y EGARCH(2,1) el que tiene menor valor de BIC y AIC es el EGARCH(1,2) Así, el modelo seleccionado para la serie de los retornos es el EGARCH(2,1), con:

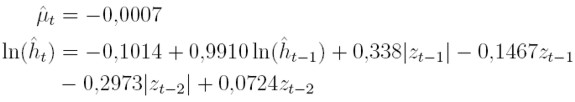donde µ_t es la media estimada, h_t es la varianza estimada y z_t = e_t / √h_t es el residual estandarizado.

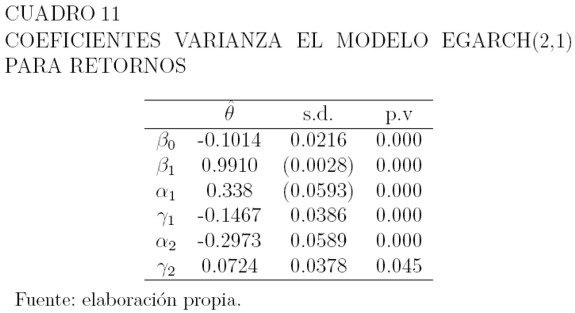
El Cuadro 11 muestra las estimaciones de los parámetros para la varianza del modelo seleccionado, el EGARCH(2,1), sus desviaciones estándar y el p-valor. La media se modela como una constante.

CONCLUSIÓN

Los modelos ARCH, GARCH y EGARCH resultan adecuados para modelar los rasgos y las características de las series financieras. En la aplicación, la serie de los precios de las acciones de Gillette, al no tener media constante, no permite una modelización a través de los EGARCH y, en este sentido, son mejores los del tipo ARCH y GARCH. En la serie de los retornos de Gillette se encuentra, como se menciona en artículos como el de Nelson (1991), que el modelo más adecuado es un EGARCH.

REFERENCIAS BIBLIOGRÁFICAS

1. Aitkin, M. (1987). " Modelling Variance Heterogeneity in Normal Regression Using GLIM: A New Approach ". Applied Statistics, 36(3): 332-339.        [ Links ]

2. Andersen, T. G. y Bollerslev, T. (1998). " Deutsche Mark Dollar Volatility: Intraday Activity Patterns, Macroeconomic Announcements, and Longer Run Dependencies ". Journal of Finance, 53(1): 219-265.        [ Links ]

3. Baillie R. T., Bollerslev T. y Mikkelsen H. (1996). " Fractionally Integrated Generalized Autoregressive Conditional Heteroskedasticity ". Journal of Econometrics, 74: 3-30.        [ Links ]

4. Bollerslev, T. (1986). " Generalized autoregressive Conditional Heterocedasticity ". Journal of Econometrics, 31: 307-327.        [ Links ]

5. Bollerslev T. y Melvin M. (1994). " Bid-Ask Spreads and the Volatility in the Foreing Exchange Market: An Empirical Analisys ". Journal of International Economics, 36: 355-372.        [ Links ]

6. Cepeda, E. y Gamerman, D. (2001). " Bayesian Modelling of Variance Heterogeneity in Normal Regression Models ". Brazilian Journal of Probability and Statistics,14: 207- 221.        [ Links ]

7. Chou R. Y. (1988). " Volatility Persistence and Stock Valuations: Some Empirical Evidence Using Garch ". Journal of Applied Econometrics, 3: 279-294.        [ Links ]

8. Engle, F. R. (1982). " Autoregressive Conditional Heterocedasticity whit Estimates of the Variance of United Kingdom Inflation ". Econometrica, 50(4), 987-1008.        [ Links ]

9. Engle, F. R. y Patton, A.J. (2001). " What a Good is a Volatility Model? ". Quantitative Finance, 1(2): 237-245.        [ Links ]

10. Engle, R. F. y Ng V. K. (1993). " Measuring and Testing the Impact of News on Volatility ". Journal of Finance, 48(5): 1749-1778.        [ Links ]

11. Engle, R.; Ito T. y Lin W-L. (1990). " Meteor Showers or Heat Waves? Heteroskedasticity Intra-Daily Volatility in the Foreing Exchange Market ". Econometrica, 58(3): 525-542.        [ Links ]

12. Engle, R. y Mezrich J. (1996). " Garch for Groups " , Risk, 9: 36-40.        [ Links ]

13. Fabozzi, F. J.; Modigliani, F. y Ferri, M. G. (1996). Mercados e Instituciones Financieras. México: Prentice Hall.        [ Links ]

14. Glosten, L. R.; Jagannathan, R. y Runkle D.E. (1993). " On the Relation between the Expected Value and the Volatility of the Nominal Excess Returns of Stocks ". Journal of Finance, 48: 1779-1801.        [ Links ]

15. Hansen P. y Lunde A. (2006). " Consistent ranking of volatility models ". Journal of Econometrics, 131: 97-121.        [ Links ]

16. Migon, H. S. y Gamerman, D. (1999). Statistical Inference: an Integrated Approach. Londres: Arnold.        [ Links ]

17. Nelson, B. D. (1991). " Conditional Heterocedasticity in Asset Returns: A New Approach ". Econometrica, 59(2): 347-370.        [ Links ]

18. Novales A. C., Gracia D. M. (1993). " Guía para la estimación de modelos ARCH ". Estadística Española, 132: 5-38.        [ Links ]

19. Ponn S. y Granger C. W. J (2003). " Forescasting Volatility in Finantial Markets: A Review ". Journal of Economic Literature, XLI: 478-539.        [ Links ]

20. Schwert G. W. (1989). " Why does stock market volatility change over time? ". Journal of Finance, 44: 1115-1153.        [ Links ]

21. Tsay, R. S. (2002). Analisys of Financial Time Series. New York: John Wiley & Sons Inc.        [ Links ]