Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista de Ingeniería
Print version ISSN 0121-4993
rev.ing. no.21 Bogotá Jan./June 2005
Generación de modelos reducidos para micro-actuadores electrostáticos
Generation of reduced models for electrostatic micro-actuators
Alba G. Ávila
Profesora, Departamento de Ingeniería Eléctrica y Electrónica Universidad de los Andes.
Carlos E. Villarraga
Asistente de Investigación, Centro de Microelectrónica Universidad de los Andes (CMUA).
Recibido el 7 de marzo de 2005, aprobado el 29 de abril de 2005
RESUMEN
El costo computacional de los análisis multifísicos necesarios en microsistemas ha exigido la creación de metodologías para generar modelos simplificados que provean resultados precisos de manera rápida y eficiente. Estas simplificaciones se conocen como la extracción del modelo de orden reducido (ROM); el modelo ROM captura comportamientos lineales y no-lineales de forma precisa, adicionalmente, dicho modelo se genera de forma tal que puede ser traspasado a simuladores de nivel de sistema. El presente artículo introduce un método automatizado para generar modelos ROM, este método se aplica al caso de una micro-viga actuada electrostáticamente; para tal estructura se muestran distintas simulaciones que caracterizan la deflexión de la estructura para diferentes excitaciones de voltaje. Los resultados muestran cómo una vez obtenido el modelo ROM se pueden llevar a cabo análisis sofisticados que son inmediatos frente al tiempo que toman las simulaciones multifísicas.
ABSTRACT
The computational cost and complexity level of multiphysics analysis used in microsystems have demanded the creation of methodologies to create simplified models that provide accurate results in a fast and efficient way. These simplifications are known as the reduced order model (ROM) extraction. The ROM model captures lineal and nolineal behaviors accurately, in addition such a model is generated in a form that can be integrated into system level simulators. This paper introduces perhaps the most famous method to generate ROM models at the present. The method is applied to the analysis of a micro clamped-clamped beam electrostatically actuated, for this structure different simulations are performed; these analyses characterize the deflection of the structure for different kinds of voltage excitations. The outcomes demonstrate that sophisticated analysis can be carried out almost immediately once the ROM model is created.
1. INTRODUCCIÓN
El proceso de diseño de microsistemas o MEMS (acrónimo en inglés de Microelectromechanical Systems) tiene como objetivo principal obtener un dispositivo final que satisfaga al máximo las características iniciales requeridas. Para lograr este propósito se han establecido diferentes metodologías de diseño que incluyen una serie de pasos iterativos como lo son análisis, simulación y construcción. Disminuir al máximo el número total de iteraciones dentro de este proceso es un problema fundamental que plantea la metodología del diseño en microelectrónica ya que su consecución permite bajar los costos de producción y reducir los tiempos de puesta en el mercado. Dentro del proceso de diseño mencionado, la etapa de análisis se puede llevar a cabo de dos maneras distintas; mediante la construcción de un prototipo de prueba o por medio de simulaciones computarizadas (prototipaje virtual). Teniendo en cuenta los costos de fabricación y los problemas técnicos que conlleva realizar el test físico de MEMS, la etapa de análisis se logra fundamentalmente con modelaje y simulación [l].
En esta etapa de análisis el principal reto que surge es la realización de simulaciones multifísicas debidas al fuerte acople entre los distintos fenómenos físicos (eléctrico, magnético, estructural y térmico etc.). Este acople se da a nivel de un mismo dispositivo como entre dispositivos "cross-talk", ejemplos de estos son: efecto piezoeléctrico y piezoresistivo, fuerzas estructurales producidas por un campo eléctrico o magnético, tensiones térmicas entre otros. Estos acoplamientos aumentan la complejidad del proceso de análisis, tanto en modelamiento como en simulación, al grado de que simular a nivel físico un microsistema, con diferentes componentes y teniendo en cuenta el detalle de cada uno de estos y su interacción conjunta, es inviable dado el costo computacional que se tiene. En consecuencia se debe recurrir a otro tipo de estrategia para la solución del problema [1].
Dentro de esta estrategia, se hace indispensable contar con un modelo ROM que tenga en cuenta únicamente los procesos relevantes que influyen en el funcionamiento del microsistema en cuestión; eliminando la redundancia que tiene una simulación con el grado de detalle mencionado. Además este modelo debe ser compacto, preciso y sencillo y se debe poder integrar a simulaciones de nivel sistema que incluyan la electrónica del caso [1].
En el presente artículo se presenta y aplica el método establecido en [3,4] para generar modelos ROM, para estructuras actuadas electrostáticamente sin pérdidas de energía. La demostración se hace a través de la herramienta ANSYS® la cual implementa el procedimiento del método referenciado. Para tal efecto se analiza una micro-viga actuada de manera electrostática, esta estructura es elemental en su concepto pero sirve como base para construir actuadores más complejos como micro-relevos, resonadores de radiofrecuencia y micro-espejos graduable entre otros.
2. DESCRIPCIÓN DE LA SOLUCIÓN
Para obtener los modelos ROM es necesario bajar hasta el nivel físico en donde se tiene suficiente detalle de las estructuras y la pérdida de información es mínima. Aunque en otros niveles de mayor abstracción también es posible obtener modelos simplificados, generalmente la precisión de estos es baja dado el poco nivel de detalle que se tiene [1,2]. Una vez obtenido el modelo es posible entonces subir de nivel y traspasarse a simuladores que operan a nivel de sistema.
Los primeros intentos hacia desarrollar una metodología para generar modelos ROM tienen sus inicios en los noventa. Sin embargo, las aproximaciones propuestas solucionaban el problema exclusivamente para el caso cuasi-estático o lineal, no obstante, a finales de 1999 se presentó un procedimiento automatizado para generar modelos de orden reducidos a partir de simulaciones físicas tridimensionales [3,4]. Esta solución, a diferencia de las técnicas desarrolladas en el pasado, desarrolla un modelo que es válido en todas las regiones de operación de la estructura involucrada (lineal y no-lineal).
2.1. RESEÑA TEÓRICA DEL MÉTODO PARA OBTENER MODELOS ROM
La figura 1 muestra el proceso para la extracción del modelo ROM. Inicialmente se tiene un dispositivo enmallado con N nodos, lo que conlleva a que se tengan 3N grados de libertad y 6N variables de estado [3]. El objetivo de la técnica es construir una representación de orden m con N >> m.
Figura 1. Fases de generación del modelo ROM
Los sistemas físicos, en particular los MEMS, en su nivel esencial se modelan por medio de ecuaciones diferenciales parciales [5] de las cuales, en la gran mayoría de los casos, no se tiene acceso directo a la solución analítica. Una aproximación común en ingeniería es aproximar la solución desconocida u(t) por medio de una serie de funciones de forma ponderadas y linealmente independientes como [3]
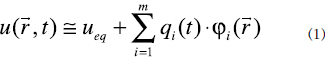
Donde qi son los factores de escala o amplitudes dependientes del tiempo, estas amplitudes son las variables desconocidas, i son las funciones de forma que caracterizan la solución y son dependientes de la posición r, en nuestro caso estas funciones son los eigenmodos del sistema lineal planteados por el equivalente en representación de variables de estado de la estructura. Como se puede observar, el cálculo del estado de deformación de la estructura se restringe ahora a una combinación lineal de m modos y el problema se convierte a encontrar m amplitudes qi, en lugar de miles de ecuaciones diferenciales ordinarias como ocurre con los análisis de elementos finitos [6]. Las funciones de forma o eigenmodos (i) de la solución se obtienen de la siguiente ecuación de movimiento de la estructura:
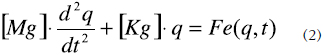
Donde Mg es la matriz de masa y Kg es la matriz de rigidez tipo constante de resorte, los valores de estas matrices se conocen de la representación nodal de la estructura; Fe es la fuerza electrostática producida por la diferencia de potencial aplicada a los electrodos. Para reducir efectivamente la dimensionalidad del problema, se deben truncar el número de ecuaciones planteadas en (2) a m. Por definición bajo condiciones controladas de voltaje la fuerza electrostática puede definirse así [5]:
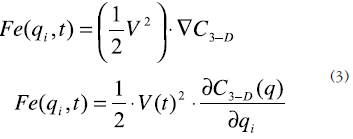
Donde C3-D representa la capacitancia total tridimensional del sistema, en [7] se demostró un método iterativo para hallar esta capacitancia en forma analítica ajustando funciones polinomiales. Combinando las ecuaciones planteadas se puede llegar a que las ecuaciones de movimiento que rigen el microsistema son:
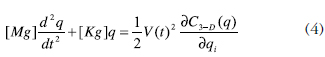
Las expresiones resultantes de (4) son ecuaciones diferenciales ordinarias (ODE) y pueden escribirse en lenguajes de descripción hardware como VHDL-AMS.
3. HERRAMIENTAS CAD PARA GENERAR MODELOS ROM
A continuación se exponen las técnicas de solución convencional (completa) y del modelo ROM para llevar a cabo las simulaciones de efectos acoplados presentados en microsistemas. En la discusión nos enfocaremos a la implementación particular que realiza la herramienta CAD para microsistemas ANSYS® en uno y otro caso. ANSYS® es un programa de simulación física bastante reconocido en microsistemas, en su método de cálculo ANSYS® se basa en la técnica numérica de los Elementos Finitos (FEM), adicionalmente, ANSYS® implementa el procedimiento para la extracción del modelo ROM discutido en la sección anterior.
3.1. SOLUCIONES CONVENCIONALES
Para solucionar numéricamente los efectos acoplados existen básicamente dos aproximaciones conocidas como la solución simultánea y la simulación separada. En la técnica de solución simultánea o directa las diferentes expresiones que describen los fenómenos individuales se unen en un sistema homogéneo de ecuaciones el cual se soluciona. La principal ventaja de este método es la posibilidad de mezclar cualesquiera modelos de continuidad temporal, lo que permite simular conjuntamente modelos obtenidos en diferentes niveles [8].
La técnica separada o secuencial realiza una división en subsistemas por dominios físicos. Este procedimiento es básicamente un método iterativo, en donde para cada uno de los subsistemas el acoplamiento de los otros subsistemas aparece como una excitación externa, para problemas estáticos, este método es igual al llamado acoplamiento por vector de carga. El acoplamiento se realiza de manera recursiva y la interacción entre los diferentes dominios se realiza hasta que se logre la convergencia.
3.2. SOLUCIÓN POR MODELOS ROM
Siguiendo la estrategia de diseño top- down, ANSYS ® divide el procedimiento de extracción del modelo ROM en tres fases [8]. La primera fase se conoce como fase de generación e incluye todos los pasos necesarios para obtener los parámetros de la simulación de modelos finitos (incluyendo la elección de los tipos de elementos y materiales), realizar el ajuste de funciones de energía y cálculo de la capacitancia tridimensional, esta etapa es la más dispendiosa computacionalmente ya que para realizar el ajuste de las funciones de energía, se deben realizar múltiples simulaciones FEM. En esta fase se produce el modelo ROM en la cual, las señales de interfaz con el exterior son para el caso electroestático: voltajes en los electrodos (entradas) y un subconjunto de desplazamientos característicos en determinados puntos estratégicos de la estructura (salidas).
En ANSYS® el modelo ROM se representa modularmente mediante el elemento esquemático ROM144 el cual se muestra en la figura 2, este elemento tiene asociados los polinomios del modelo ROM. Los puertos denominados u, q y v representan los desplazamientos o deflexiones en los puntos seleccionados, los voltajes aplicados a los electrodos y las cargas mecánicas externas respectivamente.
Figura 2. Elemento ROM144
En la segunda fase denominada fase de uso, el modelo ROM144 se utiliza en conjunto con otros elementos dentro de un mismo ambiente de simulación con el fin de realizar los análisis requeridos. Por último, la fase de expansión se encarga de solucionar el conjunto de ecuaciones diferenciales, en este caso ordinarias (ODE), y calcular las tensiones mecánicas del modelo original creado en la primera etapa de procedimiento. Dentro de la fase de generación existen dos tareas cruciales las cuales consisten en determinar las funciones base o eigenmodos que deben ser incluidos y estimar el rango de las amplitudes (desconocidas). ANSYS® ofrece distintos criterios para tomar estas decisiones, por ejemplo el diseñador puede elegir a su voluntad cuales y cuantos modos son elegidos, según sea el grado de contribución a la respuesta total del sistema. Por otra parte, los rangos de amplitud deben elegirse de forma tal que no se produzcan singularidades, por ejemplo que un electrodo toque la tierra o voltaje referencia.
4. APLICACIÓN
El uso práctico de los modelos ROM para simulación de microsistemas se aplicó a una micro-viga doblemente anclada (en inglés este tipo de estructura se conoce como clamped-clamped beam). Esta es una estructura elemental y bastante usada en microsistemas la cual sirve como base para construir otros sistemas más complicados [5], ejemplos típicos son resonadores de radiofrecuencia los cuales son útiles para implementar filtros RF, micro-interruptores (en inglés microswitches) controlados por voltaje y micro-espejos graduables entre otros.
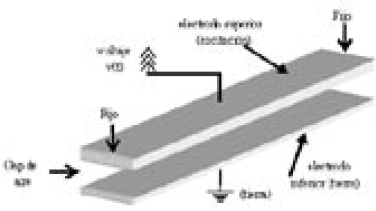
La figura 3 muestra la estructura analizada, como se observa, el mecanismo está compuesto por dos electrodos (superior e inferior). El electrodo superior se encuentra incorporado con la micro-viga la cual a su vez se encuentra anclada en sus extremos evitando el desplazamiento de la misma, esta micro-viga se deflecta debido a la fuerza electrostática producida al aplicar una diferencia de potencial entre los dos electrodos, por supuesto la cantidad de deflexión depende directamente de la magnitud del voltaje aplicado y de la rigidez del material de la micro-viga.
Figura 3. Micro-Viga Electrostática
El material (estructural) de la micro-viga es silicio y el aire entre los electrodos se considera como espacio libre en el modelo físico generado. Las dimensiones de la micro-viga en micrómetros son: largo = 80, ancho = 15 y espesor = 2, adicionalmente el "gap" de aire que se encuentra entre los dos electrodos es de 4 micrómetros.
Para crear el modelo físico, se tienen en cuenta dos elementos principales: aire (dieléctrico) y conductores (electrodos). Partiendo de esto se procede a enmallar los dos componentes para así generar los puntos de contacto entre las físicas que interactúan entre si. Antes de proceder con el proceso de extracción se debe indicar el eje de simetría donde se quieren observar las deflexiones mecánicas de la estructura, en este caso es bastante evidente y es el mismo eje de simetría de la micro-viga. En la figura 4 se ve el modelo físico creado en ANSYS®.
Figura 4. Modelo enmallado de la Micro-Viga
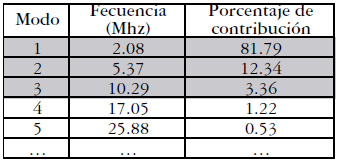
Partiendo del modelo físico se realizó la fase de generación y todas las fases subsiguientes indicadas con anterioridad. Como resultado importante se tienen los modos de operación de la estructura descritos en la tabla 1. Como se puede observar de esta tabla, los tres primeros modos tienen el mayor peso y prácticamente rigen la respuesta del sistema, la contribución conjunta de estos modos es aproximadamente del 97.5%, esto significa que si solo tomamos estos dos modos e ignoramos los modos de mayor orden, el error entre el modelo ROM y el modelo completo es del 2.5%, lo cual se puede considerar como un porcentaje de error mínimo.
Tabla 1. Relevancia de los modos de operación
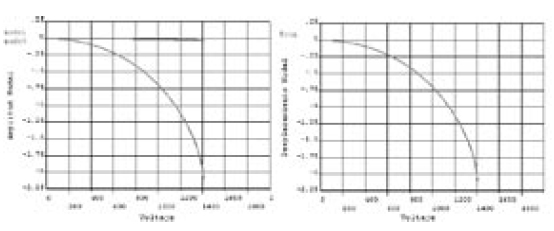
Como parte de la fase de uso se realizaron análisis convencionales similares a los que se tienen en simuladores para circuitos eléctricos, útiles para caracterizar la deflexión de la micro-viga (salida) frente a la excitación de voltaje (entrada). En primera medida se realizó un análisis estático que incluye un barrido DC de voltaje el cual traza el punto de operación de la estructura tal como se muestra en la figura 5.
Figura 5. Barrido DC. Contribución de cada modo (izquierda), Deflexión total de la micro-viga (derecha)
Adicionalmente la figura 6 muestra el resultado de un barrido de voltaje que incluye excitaciones negativas es decir produce deflexiones repulsivas. Como se observa de las figuras 5 y 6, el primer modo es dominante e influye con mucho mayor peso que el modo 3 en la respuesta total de la micro-viga. Adicionalmente como era de esperarse a mayor voltaje mayor deflexión de la micro-viga (electrodo superior), adicionalmente se observan las no-linealidades presentadas para voltajes del orden de 200 voltios.
Figura 6. Barrido DC con desplazamientos repulsivos
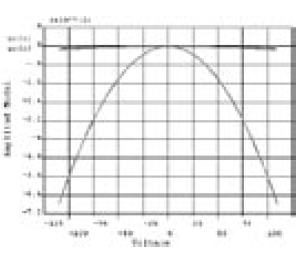
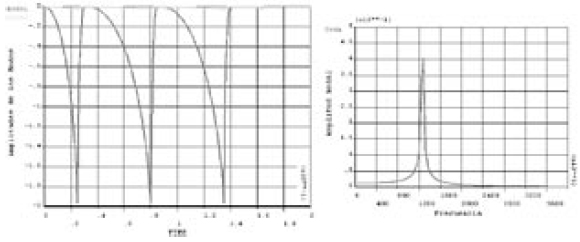
Para poder apreciar los retardos y tiempos de respuesta se realizó un análisis transiente que usa de señal de entrada una onda tipo diente de sierra, la respuesta a esta excitación es la deflexión nodal del eje de simetría de la micro-viga como se muestra en la figura 7 (izquierda) donde el desplazamiento en micrómetros es función del tiempo en segundos; como era de esperarse la contribución del primer modo es mucho más importante que la del tercero. La respuesta total de la estructura será la superpoción de estos dos modos. Por último, un análisis de función de transferencia muestra la frecuencia de resonancia debida al voltaje de polarización, este tipo de análisis harmónico es indispensable para la caracterización de actuadores y sensores. La figura 7 (derecha) muestra la respuesta en frecuencia para un voltaje de polarización de 1400 voltios.
Figura 7. Desplazamientos nodales para cada modo (izquierda), Magnitud de la respuesta en frecuencia (derecha)
5. CONCLUSIONES
Se demostró la aplicación de un método automatizado para generar modelos reducidos de microsistemas usando funciones modales bajo distintos escenarios. Los modelos generados competen las no-linealidades de acoples electrostáticos-estructurales y se pueden usar para los tipos de análisis comunes en simulaciones a nivel de sistema (DC, transiente y harmónico). Aunque en [3] se listan aplicaciones del método en cuestión (también para micro-vigas simétricas y asimétricas) allí no se muestran en detalle los diferentes análisis aquí presentados.
El método del modelo ROM agiliza notablemente la solución de efectos acoplados por dos razones básicas; la primera es que unos pocos modos representan acertadamente el comportamiento dinámico de los microsistemas actuados electrostáticamente y segundo por que tan solo una ecuación por modo y una ecuación por electrodo son necesarias para describir el efecto acoplado plenamente. Por otra parte, la aproximación generada es ideal para la descripción de microsistemas en lenguajes de alto nivel, dado que la representación final son ecuaciones diferenciales y algebraicas que son fácilmente interpretadas en herramientas que manejan lenguajes de descripción hardware (por ejemplo VHDL-AMS, Verilog entre otros).
En cuanto a tiempos de simulación se obtuvo que la solución de una simulación completa usando el método secuencial tomó aproximadamente una hora en el análisis estático (DC) (el cual es el mas básico de todos los análisis posibles); mientras que con el método del modelo ROM la generación del modelo ROM gastó 25 minutos y cualquiera de los análisis realizados no demoró más de un minuto. Esto demuestra la reducción en tiempo de simulación, lo cual es fundamental en la simulación a nivel de sistema.
Como siguiente paso se tiene el uso del código VHDL-AMS generado por ANSYS® para integrarse a una herramienta de nivel de sistema EDA como Virtuoso de Cadence ®, Synopsys® o Simulink de Matlab ®, Adicionalmente se estudiarán nuevas estructuras más complejas que tengan una aplicación más directa a problemas reales de ciencias e ingeniería.
NOTA DE LOS AUTORES
Resultados adicionales de esta investigación fueron publicados en el pasado "XI IBERCHIP Workshop" celebrado el 28 de Marzo del presente año en el artículo titulado "GENERATION OF REDUCED ORDER MODELS IN MICROSYSTEMS CASE: ELECTROSTATIC CLAMPED-CLAMPED BEAM".
6. REFERENCIAS BIBLIOGRÁFICAS
[1] S., Senturia, N.; Aluru, y Jacobwhite. Simulating the Behavior of MEMS Devices: Computational Methods and Needs. IEEE Computational Science & Engineering, 1997. [ Links ]
[2] S. Senturia. Microsystem Design 4th printing. Kluwer Academic Publishers, 2002. [ Links ]
[3] L., Gabbay ; J., Mehner y S, Senturia. "Computer-aided Generation of Reduced-order Dynamic Macromodels -I: Geometrically Linear Motion". En J. Microelectromech. Syst. vol. 9, pp. 262-269, Junio 2000. [ Links ]
[4] J., Mehner ; L., Gabbay, y S., Senturia. "Computer-aided generation of nonlinear reduced-order dynamic macromodels -II: Stress-stiffened motion". En J. Microelectromechanical Sys. vol. 9, pp. 270-278, Junio 2000. [ Links ]
[5] J., Pelesko y D., Bernstein. Modeling MEMS and NEMS. CRC Press, 2003. [ Links ]
[6] E., Hung y S., Senturia. "Generating efficient dynamical models for microelectromechanical systems from a few finite-element simulation runs". En J. Microelectromech. Syst. vol. 8, pp. 280-289, Septiembre, 1999. [ Links ]
[7] K. Nabors y J. White. " FastCap: Amultipole -accelerated 3-D capacitance extraction program". En IEEE Trans. Computer-Aided Design vol. 10, pp. 1447-1459, Noviembre, 1991. [ Links ]
[8] ANSYS, Inc. Theory Referente, Release 8.0 Documentation Copyright © 2003. [ Links ]