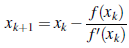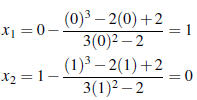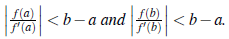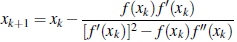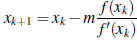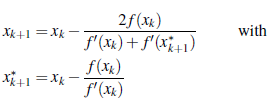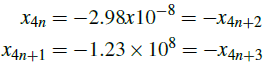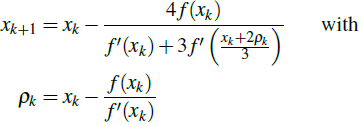1 Introduction

Nonlinear equations and its applications have been widely studied; currently, we know that if the equation is not soluble via analytical methods, we can use numerical methods to solve it [¹⁰]. Thus, numerical methods for finding roots are continually being developed cf. [¹⁴].

The Newton-Raphson method, named after Isaac Newton (1643-1727) and Joseph Raphson (1648-1715), is a well-known method for finding roots given by the following recurrence relation

Hence considering an initial guess x₀, the formula above can be used to calculate x₁, x₂ and so on, we would stop once |x_k+1 - x_k | < ε, for a given ε value cf. [⁴]. Due to the geometrical meaning the Newton-Raphson method is also known as the method of tangents [¹⁸]. Thomas Simpson (1710-1761) introduces an extension of this method for system of equations [⁵].

A Matlab code such that the function is typed by the user via keyboard and the derivative is calculated by Matlab (requires symbolic variables), considering as parameters: x₀ the initial guess, n the number of iterations and tol the tolerance, or the maximum error ε, is given as follows.

The above code is slower than a code with anonymous functions instead of symbolic variables [¹²]. Other programming languages can be used to implement the method, among them Python [¹¹]. There are examples such that Newton-Raphson method, also known as Newton's method [²⁰], jumps between two values; for instance, f (x) = x³ - 2x + 2 with x₀ = 0 cf. [⁹]. Since f'(x) = 3x² - 2, we have

Thus, for any n ≥ 0 we have x_2n = 0 and x_2n+₁ = 1. High sensitivity of the Newton-Raphson method on starting values is verified by f (x) = sin(x) in the following table, where x₀ is the initial guess and x* is the value to which the method converges starting from x0.

Table 1 Convergence of Newton-Raphson method for f (x) = sin(x) with several initial guesses. 

Under certain conditions the convergence of Newton-Raphson method is quadratic [⁶], it can be verified that the Newton-Raphson method converges linearly near zeros having multiplicity greater than 1 cf. [³]; however, we note that the recurrence can become numerically unstable, and may not converge, if f'(x _k ) is close to zero. The following theorem is a global convergence theorem for Newton-Raphson method, proof can be found in [¹].

Theorem 1. Let f G C²([a, b]) satisfy the following conditions:

1. f (a) f (b) < 0 and f' (x) ≠ 0, for all x Є [a, b].

2. Either f''(x) ≥ 0 for all x Є [a, b] or else f''(x) ≤ 0 for all x Є [a,b].

3.

Then f has a unique zero x* Є (a, b) and the Newton-Raphson method converges to x* for any initial guess x ₀ ∉ (a, b).

It is not easy to verify the hypotheses of the global convergence theorem, mainly due to the difficulty of determining a and b, thus in some cases for the function f (x) there are a and b such that satisfies the conditions for convergence but x₀ ∉ (a, b).

To improve students' numerical and analytical thinking abilities, we present some limitations of the Newton-Raphson method. We aim to show several modified Newton-Raphson methods, generate a code for each method, and even compare them to study the numerical stability and convergence of these methods via examples.

2 Methods

Multiple roots bring some difficulties to Newton-Raphson method, thus Anthony Ralston and Philip Rabinowitz (1926-2006) introduce the following modification cf. [¹⁶]

The formula above is known as modified Newton-Raphson method for multiple roots [²], in this way we avoid the singularity due to f' (xk) = 0. Although it is a good option for multiple roots, this method requires more computational effort than the classical method. Ralston and Rabinowitz also introduce the modified method, also known as relaxed Newton's method [⁷], given by the following recurrence

Where m is the multiplicity of the root. It is easy to check that the classical Newton-Raphson method is the case m = 1. we may verify that f(x) = x ³ -2x+2havejustarealroot, r= -1.769292with multiplicity 1; however, by applying the modified Newton-Raphson method for multiple roots on f( x) = x ³ - 2x + 2 with initial guess x0 = 0, we obtain x₁₀ = -1.769292. On the other hand, by the relaxed Newton's method with m = 2 we have a slow convergent method, with m = 3 we get x_2n = 0.2416943 and x_2n+1 = 2.7583057 for any n ≥ 2.

Recently, predictor-corrector strategies were used to improve Newton-Raphson method, among them we find the recurrence relation

The formula above is a third order of convergence method [²³]. A modified method with convergence of order 1 + √2 can be found in [¹³], that method is given by the recurrence relation

where x ^* ₀ = x₀ - 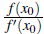. It is easy to verify that if x ₀ ^* = x0 we get the classical method.

By applying the predictor-corrector methods to f(x) = x ³ - 2x + 2 with initial guess x ₀ = 0 we find the root r = -1.769292; but for this case, both predictor-corrector methods are slower than the modified method for multiple roots.

3 Results

In this section we test the presented methods with the following problem, use the Newton-Raphson method and its modifications to estimate a root of f(x) = - x ⁴ + 6x ² + 11 employing an initial guess of x0 = 1. On the other hand, we consider the family of complex polynomials p_n(z) = z ⁿ + 1 to generate fractals as visual representations of the sensitivity on starting values.

By the classical method we have x2n = 1 and x_2n+₁ = -1 for any n ≥ 0. We obtain the same result with the modified Newton-Raphson method for multiple roots. For the relaxed Newton's method, given by the recurrence x_k+1 = x _k -m 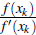, in the following table we present the result obtained by applying several iterations taking m = 2, 3 and 4.

Table 2 Relaxed Newton-Raphson method with f(x) = -x⁴ + 6x² + 11 and initial guess x₀ = 1, considering m = 2,3 and 4. 

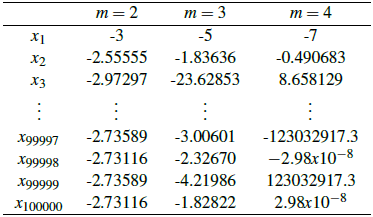
For the relaxed Newton's method with m = 2 we have a slow convergent method. For m = 3 we have an unstable non-convergent method and for m = 4 we get a method such that, for large values n the result jumps between

The predictor-corrector methods diverge, in both methods the denominator of the recurrence formula in the calculation of x₁ is 0. Hence, for f (x) = -x⁴ + 6x² +11 with initial guess x₀ = 1, the Newton-Raphson method and the modifications considered in this paper do not have a good performance. However, we can use a modification of Newton-Raphson method with cubic convergence cf. [⁸], given by the recurrence relation

It is easy to verify that if ρ _k = x _k we get the classical Newton-Raphson method. As an interesting fact, by applying the above recurrence to f (x) = - x ⁴ + 6x ² + 11 with initial guess x0 = 1 we obtain the root x8 = 2.733521.

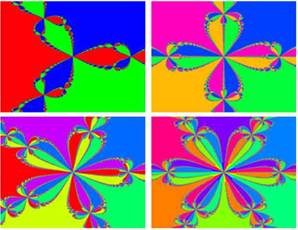
In 1789, Arthur Cayley noted the difficulties in generalizing Newton's method to compute complex roots of polynomials with degree n > 2 cf. [¹⁷]. Since the complex polynomial p _n(z) = z ⁿ + 1 have n different roots [²²], we assign a color to each root and we take a region of the complex plane to apply the Newton-Raphson method for each point, with the point as initial value; thus each point in the region takes the color of the root to which it converges. Hence, we get an interesting visual representation known as Newton's fractal [¹⁹].

Figure 1 Newton's fractals for n=3,4,5 and 6. 

This idea can be extended to another kind of polynomials cf. [²¹] and methods. Here we use the relaxed Newton's method for generating fractals with family of polynomials p _n (z) = z ⁿ + 1.

Figure 2 Fractal obtained by the relaxed Newton's method with m = 2, for n = 3, 4, 5 and 6. 

Fractals can be generated via the relaxed Newton's method with another families of polynomial cf. [¹⁵]. Since fractals are obtained through the instability of the Newton-Raphson method, we may ignore the meaning of m in the relaxed Newton's method to consider non-integers values for generating fractals.

Figure 3 Fractal obtained by the relaxed Newton's method with m = 1.5 and n = 5. 

4 Conclusions

To improve the student's skills in algorithmic thinking in numerical analysis courses, the implementation of several modified Newton-Raphson methods starting with a code of the classical Newton-Raphson method can be considered as an activity with the motivation of performing a comparison among them.

Given a function, to find a and b such that satisfies the global convergence theorem for Newton-Raphson method is a challenge that can be considered in a course for students of mathematics or students interested in theorical numerical analysis.

Special cases such as the one considered in the section Results are helpful for preparing numerical analysis exams in platforms like Moodle since we can create several kinds of questions. For instance: multiple choice, we may ask which of the following modified Newton-Raphson methods converges; computed numeric, in which case we can ask for the result after performing a given number of iterations; justify a response, since we can ask to explain why the obtained result after performing some of the modified methods or compare the results obtained by several of those methods. Even programming questions, to implement one of the modified Newton-Raphson methods from the code of the classical Newton-Raphson method.

The Newton fractal is a visual representation of the high sensitivity of the Newton-Raphson method on starting values, similar ideas through modified methods can be an interesting activity to consider in a numerical analysis course, here the teacher's role will be to guide the students on the use of programming languages for generating visual representations.