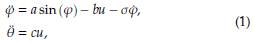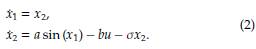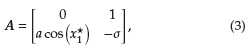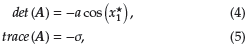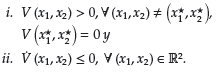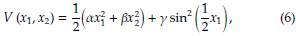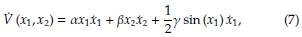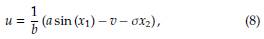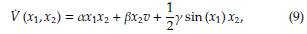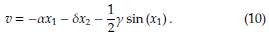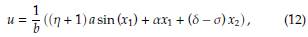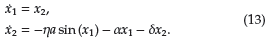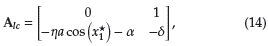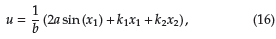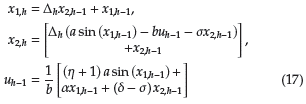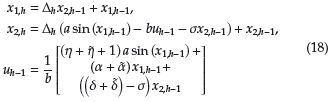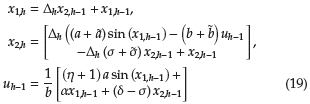Spanish (pdf)
Article in xml format
Article references
Automatic translation
Send this article by e-mail
Cited by SciELO 
Cited by Google 
Similars in
SciELO 
Similars in Google 
Permalink
1. Introducción
Los sistemas dinámicos están presentes en muchos procesos de nuestra vida cotidiana, tanto a nivel comercial como industrial. Estos sistemas, a menudo complejos y no lineales, requieren controles efectivos para llevar a cabo tareas específicas [1]. Para diseñar un control efectivo, se requiere realizar investigación y desarrollo de estrategias novedosas las cuales pueden ser aplicadas a sistemas dinámicos lineales y no lineales. Sin embargo, estos controles antes de ser implementes en los sistemas reales son evaluados en sistemas de prueba con características similares a los sistemas reales [2]. Estos sistemas de prueba o prototipo juegan un papel fundamental en la validación del desempeño de los controles ya que permiten comprender el comportamiento de estos sistemas dinámicos y así los control pueden ser simplificados y ajustados más fácilmente en el momento de su implementación [3]. Ejemplo claro de este proceso es la aplicación de los controles en un péndulo, ya que es un sistema pequeño pero de alta complejidad y permite evaluar la efectividad de los controladores. Existen varios tipos de péndulo como los son: rueda de reacción, Pendubot, Acrobot, entre otros [4]. Estos tipos de péndulos permiten emular los retos de sistemas dinámicos complejos reales, como: máquinas síncronas conectadas a un barraje infinito, drones, robots (caminantes o móviles), cohetes, aeronaves, entre otros [5, 6].
El péndulo con rueda de reacción (RWP) es uno de los péndulos más estudiados debido a su complejidad dinámica y su versatilidad en aplicaciones prácticas y académicas. Este péndulo es un variedad del péndulo simple, el cual consiste en una masa suspendida de un punto fijo. El RWP fue propuesto por Spong en [5] incorporando una rueda de inercia que puede rotar alrededor de su propio eje. Esta rueda genera nuevos elementos dinámicos y comportamientos no lineales en el sistema, lo que lo convierte en un objeto de estudio fascinante para investigadores y académicos en campos como la ingeniería, la física y la robótica [7]. Esto es debido que este péndulo enfrenta dos principales desafíos. El primer desafió (local) radica en garantizar la estabilidad del péndulo en el punto de equilibrio [8]. Mientras que el segundo desafío radica en elevar o subir el péndulo desde suposición inicial o de reposo (abajo) hasta su punto de equilibrio (arriba). Este desafío también es conocido como balanceo o "swing-up"[9]. El segundo desafío prácticamente se encuentra ya resuelto y ha sido resuelto exitosamente usando estrategias de control basadas en energía [7,10,11].
Con el objetivo de abordar el primer desafío mencionado para el RWP, se han propuesto diversos controladores lineales y no lineales. Los controladores lineales pueden ser efectivos cuando se diseñan cerca del punto de equilibrio, utilizando métodos de linealización como series de Taylor o aproximaciones trigonométricas [12,13]. Aunque estas linealizaciones son altamente efectivas en las proximidades del punto de equilibrio, la estabilidad de estos controladores se ve comprometida cuando el RWP se ve afectado por disturbios o eventos externos que lo alejan de su punto de equilibrio, lo que invalida la aproximación lineal [14]. Para evitar estos posibles problemas de estabilidad, se han propuesto controladores no lineales que ofrecen un buen rendimiento y pueden operar en puntos alejados del equilibrio del sistema. Estos controladores incluyen la linealización exacta o parcialmente retroalimentada [15], control deslizante de funciones [16], lógica difusa [17], control basado en pasividad [14], redes neuronales artificiales [9], control óptimo [4], control robusto [18] y control basado en Lyapunov [7], entre otros. A pesar de que estos controladores han demostrado un buen desempeño en diversas condiciones de simulación, algunos de ellos no garantizan la estabilidad o pueden presentar problemas de oscilación cerca del punto de equilibrio. Otros controladores requieren una sintonización meticulosa de múltiples parámetros o reglas de operación, lo cual puede dificultar su implementación. Además, algunos controladores necesitan realizar optimizaciones en tiempo real, lo que puede ser problemático debido a los altos requisitos de hardware y precisión [13]. Si bien es cierto que algunos de estos controladores aseguran la estabilidad del sistema en lazo cerrado, su implementación puede ser compleja.
En la Tabla 1 se presenta un resumen de las principales metodologías de control aplicadas al diseño de controladores para el RWP.
De la Tabla 1 se destaca que, aunque es un sistema dinámico clásico, este continua siendo un sistema de gran interés en la literatura científica en la validación de metodologías de control con propiedades de estabilización locales y globales. Considerando la revisión del estado del arte y el resumen de metodologías de control presentado en la Tabla 1, en este artículo se presentan las siguientes contribuciones:
i. El diseño de un controlador general basado en una función candidata de Lyapunov para el RWP que permite convertir el punto de equilibrio inestable de la barra en su posición vertical superior de un comportamiento tipo silla a un comportamiento tipo foco estable.
ii. En análisis en simulación considerando incertidumbre paramétrica en las constantes del RWP, así como teniendo en cuenta variaciones de las ganancias de control, con el objetivo de estudiar su efecto en los tiempos de establecimiento del sistema.
Es importante mencionar que, a diferencia del diseño de control basado en Lyapunov presentado por los autores de [7], en este trabajo se generaliza el diseño de control a través de una función candidata de Lyapunov, que permite, según la selección de las constantes de control, obtener una ley de control que: (i) puede ser obtenida a partir el método de linealización exacta de las variables de estado (ver Ref. [22]), (ii) equivalente a la formulación de Lyapunov dada por los autores de [7], o (iii) una familia de controladores no lineales que garantizan un comportamiento estable para el RWP en su posición de equilibrio vertical superior.
Este artículo está organizado de la siguiente forma: La sección 2 presenta el modelo dinámico del RWP mientras que la sección 3 calcula sus puntos críticos. La sección 4 describe el diseño del control para el RWP basado en la teórica de Lyapunov. La sección 5 realiza las validaciones numéricos del control propuesto y un análisis perimétrico. Finalmente, la sección 6 presenta las conclusiones más importantes de este trabajo, así como también los posibles trabajo futuros.
Tabla 1: Principales métodos de control aplicados al RWP
| Metodología de diseño del controlador | Local | Gobal | Año | Ref. |
|---|---|---|---|---|
| Control no lineal basado en realimentación de las variables de estado | ✓ | 2001 | [5] | |
| Control mediante linealización exacta de las variables de estado | ✓ | 2007 | [12] | |
| Control basado en lógica difusa | ✓ | 2013 | [12] | |
| Linealización exacta de las variable de estado y funciones de energía | ✓ | 2014 | [6] | |
| Control difuso usando seguimiento de trayectoria | ✓ | 2017 | [13] | |
| Control por realimentación de variables de estado empleando funciones de Lyapunov | ✓ | 2020 | [7] | |
| Control óptimo inverso mediante relimentación pasiva | ✓ | 2020 | [4] | |
| Control óptimo inverso empleando funciones de Lyapunov | ✓ | 2020 | [19] | |
| Estabilización por realimentación de salida mediante control activo de rechazo de perturbaciones | ✓ | 2023 | [20] | |
| Control proporcional-integral-derivativo y linealización de las variables de estado | ✓ | 2024 | [21] |
2. Modelo dinámico del RWP
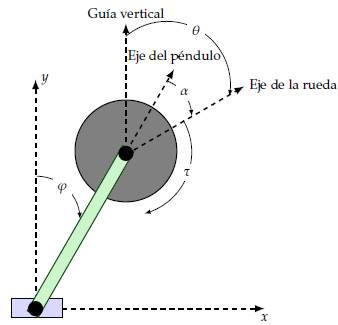
La representación esquemática del RWP se presenta en la Figura 1, donde se presentan las principales variables de este sistema, es decir, la posición angular de la barra pendular respecto del eje vertical, i.e., p, la posición relativa del ángulo de la rueda respecto del eje móvil asociado al péndulo, i.e., φ. La posición angular relativa de la rueda de reacción se define sobre el marco de referencia fijo como θ. Nótese que θ = α + φ. Además, se muestra el efecto del torque aplicado por el motor conectado a la rueda de reacción, el cual se define como t.
Según los autores de [13], el modelo dinámico del péndulo con rueda de reacción se define según se presenta el sistema de ecuaciones dado por (1).
donde a, b y c son constantes relacionadas con los parámetros físicos del sistema y σ define el coeficiente de friccion dinamica del péndulo con el aire. Para la implementación del diseño de control, dado que el comportamiento de la variable θ se define como la integral doble de la entrada de control, no es necesario incluirla en la representación de la variable de estado como se recomienda en [7]. Con el objetivo de obtener la representación equivalente del péndulo con en términos de las variables de estado, se define x1 = φ y x2 = ẋ1. Con lo anterior, la primera Ecuación de (1), se representa como sigue:
Notese que el sistema dinamico dado en (2) corresponde a un sistema no lineal de segundo orden con infinitos puntos de equilibrio ciclicos cuando la entrada de control es nula, i.e., u = 0, los cuales se dan cuando ẋ1 = 0 y ẋ2 = 0, es decir, x*k = (kπ, 0) , ∀k ∈ N. Estos puntos de equilibrio son ciclicos, ya que el movimiento del RWP se da sobre un plano circular, con lo cual, los puntos de equilibrio se dan en la parte vertical superior y vertical inferior de la Figura 1, i.e., p1 (0, 0) y p2 (π, 0), respectivamente.
3. Puntos de equilibrio y estabilidad en lazo abierto
Con el fin de determinar el comportamiento del RWP alrededor de sus puntos de equilibrio, considere el siguiente teorema, aplicable a puntos de equilibrio alrededor de su punto de operacion:
Teorema 1 (Estabilidad alrededor del punto de equilibrio)
El sistema dinamico (2) linealizado alrededor de sus puntos de equilibrio en lazo abierto, i.e., Δ˙x = AΔx, siendo A la matriz Jacobiana del sistema, se tiene que [23,24]:
i. En p1: Si det (A) < 0, entonces el sistema dinamico tiene un punto de silla.
ii. En p2, si det (A) > 0, trace2 (A)−4det (A) < 0, y trace (A) < 0 entonces el sistema dinamico tendra un foco estable.
Demostración 1 La matriz A para el sistema dinámico dado en (2) toma la forma:
siendo x * 1 el punto de equilibrio asociado a la variable de estado x 1 . Teniendo en cuenta los operadores determinante y traza (ver Ref. [23]), se tiene:
Por lo tanto, al evaluar las condiciones del Teorema 1 en los puntos de equilibrio p1 y p2, se tiene:
■ En p 1 , x* 1 = 0, con lo cual: det (A) = -a < 0, lo que confirma que este es un punto de silla inestable.
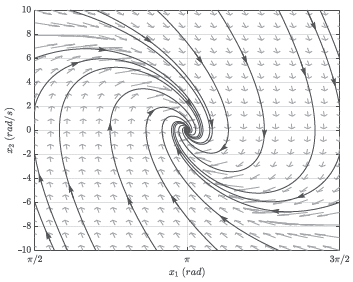
■ En p 2 , x* 1 = ϖ, con lo cual: det (A) = a > 0, como la traza es constante y negativa, i.e., trace (A) = -a, se verifica que trace 2 (A) - 4 det (A) = σ 2 - 4a < 0 (ya que el parámetro a es mucho mayor que el coeficiente de fricción a), lo que confirma que este es foco estable.
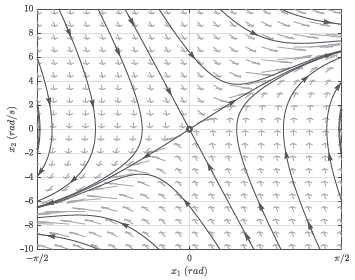
Con el objetivo de ilustrar gráficamente el comportamiento del RWP, se toman los valores reportados en [22], para los parámetros a, b y c son 78,4, 1,08 y 198, respectivamente. Además, para efectos de simulación, se asume un coeficiente de fricción a = 10 (únicamente para efectos ilustrativos), con lo cual se obtienen los resultados presentados en las Figuras 2 y 3.
Observación 1 En caso de que el coeficiente de fricción sea despreciado, i.e., a = 0, el comportamiento del punto de equilibrio p1 no cambia y permanece siendo un punto de silla inestable; sin embargo, para el caso del punto p 2 estepasaría de ser un foco estable a un centro [23].
Por otro lado, teniendo en cuenta el comportamiento dinámico del RWP alrededor de los puntos de operación p1 y p2, el objetivo de diseño de un controlador para este sistema, radica en encontrar una ley de control u, tal que el punto de silla en p 1 se convierta en un punto de equilibrio estable, es decir, un foco o un nodo estable [7]. Para esto, en la siguiente sección se plantea el diseño de control a través de la teoría Lyapunov.
4. Diseño de control basado en Lyapunov
La teoría de Laypunov es ampliamente conocida en el área de control, ya que es una herramienta robusta para probar estabilidad de puntos de equilibrio de sistemas dinámicos no lineales [25]. Esta teoría es extendida al área de control, con el objetivo de terminar la forma que debe tomar una ley de control u, para llevar un punto de equilibrio inestable en lazo abierto a una operación estable en lazo cerrado [7]. La principal dificultad de esta teoría radica en la selección de la función de Lyapunov, i.e., V (x 1, x 2) para el caso de estudio, tal que en el punto de equilibrio p(x 1 *, x2*) se cumplan las condiciones enunciadas en el siguiente teorema.
Teorema 2 Estabilidad en el sentido de Lyapunov
Sea V (x1, x2) una función candidata de Laypunov, entonces el punto de equilibrio p (x 1 *, x2*) será estable, si y solo si:
Observación 2 El Teorema 2 quiere decir, que una punto de equilibrio es estable, si la función candidata de Lyapunov V (x 1, x 2) es definida positiva para todo punto en ℝ2, nula en el punto de equilibrio, y su derivada temporal es semidefinida negativa en ℝ2.
Es importante mencionar que aunque pueden existir múltiples funciones de Lyapunov que permitan cumplir las condiciones del Teorema 2, el reto principal de esta teoría radica encontrar por lo menos una función candidata que lo cumpla. A continuación, se presenta el desarrollo de una estrategia de control a partir de la teoria de Lyapunov.
4.1. Diseño del controlador
Para obtener una ley de control u que satisfaga el Teorema 2 alrededor del punto de equilibrio (x 1 * , x 2 * ) = (0, 0), es decir, en la posición vertical superior de la barra, considere la función candidata de Lyapunov dada en la Ecuación (6).
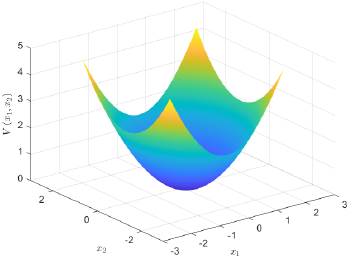
donde los parámetros α, β y γ se definen en el conjunto de los números reales positivos (estos son parámetros de diseño del controlador). Nótese que V (x1, x2) en (6) cumple la primera condición del Teorema 2, ya que V (0,0) = 0 y V (x1, x2) > 0, ∀ (x1, x2) ≠ (x 1 * , x 2 * ). La forma de esta función candidata de Lyapunov se presenta en la Figura 4 (donde se asumen valores unitarios para α, β y γ, únicamente con fines ilustrativos).
Ahora, la derivada temporal de la función candidata de Lyapunov dada en (6), se presenta a continuación:
Para determinar, si la Ecuación (7) cumple con la segunda condición del Teorema 2, se requiere sustituir el sistema dinámico dado en (2) y realizar algunas manipulaciones algebraicas. Para esto, en primer lugar se define la ley de control, según la Ecuación (8)
siendo v una variable auxiliar de control, con lo que al sustituir en (7), se tiene:
de la cual se puede definir la variable auxiliar de control v como sigue:
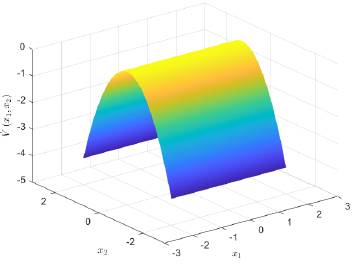
Ahora, si el parámetro β se define como la unidad, i.e., β = 1, entonces al sustituir la ley de control auxiliar dada en (10) en la derivada temporal de la función de Lyapunov (9), se obtiene:
lo cual confirma la segunda condición del Teorema 2 si y sólo el parámetro δ > 0, con lo cual el punto de equilibrio será estable, siendo la derivada temporal de la función de Lyapunov, la que se muestra en la Figura 5.
Observación 3 La ley de control obtenida para este esquema de control toma la forma (12)
donde y se ha definido como 2 (η + 1) a, siendo r¡ una constante positiva.
Observación 4 En el diseño de controladores no lineales para sistemas dinámicos utilizando funciones de Lyapunov, es posible encontrar una amplia variedad de funciones que aseguran la estabilización del sistema [23]. Por lo tanto, la elección de la función de Lyapunov adecuada depende de los requisitos específicos del diseño del controlador y de las condiciones de operación en lazo cerrado que se deseen satisfacer.
4.2. Análisis en lazo cerrado
En esta subsección se presenta el análisis de la estabilidad para el RWP dado en (2), cuando le es aplicada la ley de control dada en (12). El sistema en lazo cerrado, toma la forma dada en (13).
cuyo único punto de equilibrio está dado en el origen, i.e., p1 (x 1 * , x 2 * ) = p1 (0,0).
Linealizado el sistema dinámico en lazo cerrado dado en (13), se tiene la matriz de lazo cerrado A lc que se muestra:
Aplicando el Teorema 1 a la matriz A lc se tiene que para el punto de equilibrio: det (A lc ) = ηαcos (x* 1) + α = ηα + α > 0, además, trace (A lc ) = -δ y trace2 (A) - 4det (A) = δ2 -4 (ηα + α) < 0 (si y sólo si 4 (ηα + α) > δ2, lo cual se logra definiendo adecuadamente los parámetros de control α, η y δ2. Lo anterior, implica que el punto de equilibrio en lazo cerrado corresponde a un foco, ya que se cumple la segunda condición del Teorema 1.
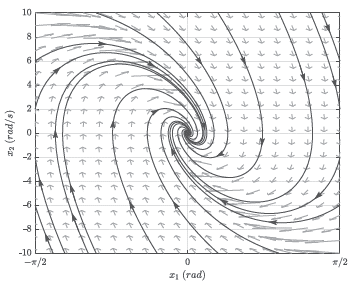
Para ilustrar la condición anterior, se realiza el retrato de fase para el sistema dinámico de lazo cerrado dado en (13), definiendo por simplicidad para la gráfica, ¡ se asigna en 1, mientras que α y δ toman el valor de 10. En la Figura 6 se presenta el comporamiento del RWP en lazo cerrado, que demuestra gráficamente que el punto de equilibrio en la parte vertical superior es un foco estable.
4.3. Generalización de la ley de control
Una contribución fundamental de este trabajo corresponde a la generalización de la ley de control definida en términos de las ganancias de control α, δ y η, como se observa en (12). Con lo cual, se pueden obtener una familia de controladores, que en un caso corresponde al método de linealización exacta presentado en [22], y otro caso al controlador basado en Lyapunov presentado en [7].
Para el caso de la linealización exacta propuesta por los autores de [22], se selección el parámetro ¡ en cero, α = k1 y δ = σ + k 2 lo cual produce la ley de control definida en (15)
En el caso del controlador basado en Lyapunov presentado por los autores de [7], se selecciona el parámetro η como la unidad, mientras que los parámetros α y δ toman la misma forma del caso anterior, con lo cual se obtiene la ley de control dada en (16)
Observación 5 Nótese que la ley de control dada en (12) es, por tanto, una ley de control general que produce una familia de controladores no lineales para el RWP, que además, puede ser ajustada en función de los requerimientos de la planta y el desempeño dinámico requerido.
5. Validaciones numéricas en simulación
En este apartado, se presentan las validaciones numéricas para el RWP considerado los parámetros a, b y c definidos en la Sección 2. Sin embargo, es importante tener en cuenta, que aunque la ley de control es global, teniendo en cuenta las características del RWP descritas en [26], se asumen que la ley de control admisible se aplica en el rango de -10 ≤ u ≤ 10. Teniendo en cuenta lo anterior, se plantean dos escenarios de simulación, como sigue:
i. Se asume que los parámetros del RWP, i.e., a, b y c son perfectamente conocidos y no presentan incertidumbre. Se seleccionan las ganancias de control α, β y η como 3500, 135 y 1 (ver referencia [19]). Se realizan variaciones aleatorias en un rango de ±20 % alrededor de estos valores y se obtiene el desempeño de las variables de estado respecto del tiempo.
ii. Se fijan los valores de las ganancias de control α, β y η como 3500,135 y 1, respectivamente, y se realizan variaciones perimétricas a los parámetros del RWP a y b en ±5 % respecto de su valor nominal de manera aleatoria y se obtiene el desempeño de las variables de estado respecto del tiempo.
Nótese que para los dos primeros escenarios, se asume que el RWP se ha llevado a una región cercana al punto de equilibrio en la posición vertical superior, esto es, x0 1 = 7o y x0 2 = 0 rad. Además, se considera que el coeficiente de fricción dinámica con el aire es despreciable, es decir, σ = 0.
Observación 6 Para facilitar el proceso de simulación, el sistema dinámico dado en (2) y la ley de control presentada en (12) son discretrizadas, mediante el método de derivada hacia adelante [4], con lo cual se tiene:
5.1. Variación de ganancias del controlador
En este escenario se realizan variaciones sobre las ganancias de control, con el fin de observar su efecto en la dinámica del sistema. Estas variaciones se dan en un rango de ±20 % respecto de sus valores de referencia. Nótese que el sistema dinámico simulado para este escenario corresponde al definido en (18).
donde
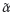y
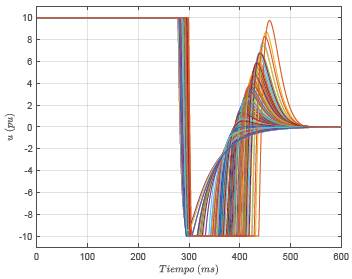
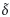representan las variaciones de las ganancias de control α y β en el rango de ±20 % siendo estos generados con una distribución de probabilidad uniforme. En las Figuras 7, 8 y 9 se presenta el comportamiento dinámico de la posición angular de la barra pendular, su velocidad, y la señal de control aplicada, respectivamente. El sistema simulado en este caso corresponde al definido en (??).
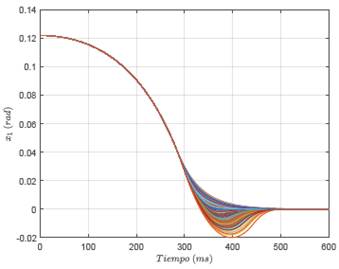
Del comportamiento dinámico de las variables de estado, así como de la ley de control dadas en la Figuras 7, 8 y 9, es posible notar que:
i. Las variables de estado, i.e., la posición y la velocidad angular de la barra se estabilizan en sus valores de referencia entre los 400 ms y los 00 ms. Lo cual se debe a las variaciones de los parámetros de control aplicados a este sistema. En el caso de la posición angular de la barra, es posible observa que existen combinaciones de ganancias de control que generan una tendencia al punto de equilibrio sin oscilaciones, es decir, sin sobrepaso, que son aquellas para los cuales la barra pendular se estabiliza más rápido (ver Figura 7), i.e., alrededor de los 400 ms.
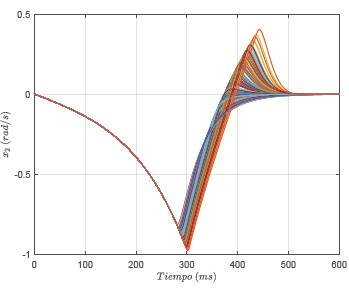
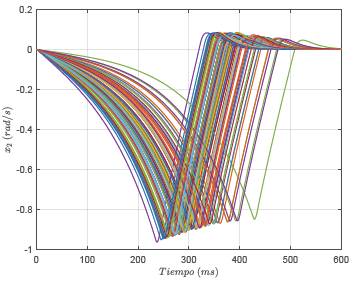
ii. La respuesta dinámica de la velocidad muestra el comportamiento esperado para un sistema pendular (ver Figura 7), ya que esta inicialmente sufre una aceleración que aumenta su velocidad, lo que a su vez lleva el bazo pendular más cerca de su posición de equilibrio. Luego, esta se desacelera, lo que produce una reducción en la velocidad, hasta hacerse nula en el punto de equilibrio. Nótese que existen combinaciones de parámetros en las ganancias de control, para los cuales la velocidad del péndulo cambia de signo, lo que implica que, un sobrepaso respecto del punto de referencia de interés, con lo cual, el péndulo debe ser acelerado en el otro sentido de movimiento, para hacer que este llegue nuevamente a su punto de referencia.
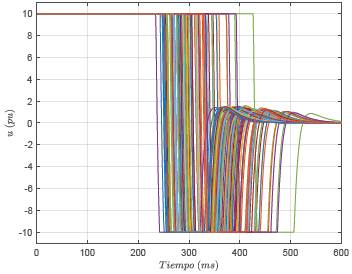
iii. En cuanto a la dinámica de la ley de control presentada en la Figura 9, se observa que: (a) esta se encuentra en saturación durante los primeros 300 ms, es decir, la rueda de reacción se acelera hasta alcanzar su velocidad nominal (saturación para u = +10 pu), y se mantiene constante, posteriormente esta es desacelerada y cambia su sentido de giro (saturación para u = +10 pu), con el fin de frenar la velocidad de rotación de la barra pendular, y (b) después de los 400 ms se observa una variación de la velocidad de rotación de la rueda (equivalente a la ley de control), tal que si existen sobrepasos en el punto de equilibrio del péndulo está cambia de signo, en caso contrario, esta converge a cero, cuando se han regulado las variables de estado del RWP en su punto de operación.
5.2. Variación de los parámetros del RWP
En este escenario de simulación se analiza el caso en el que los parámetros del RWP varían para la planta, i.e., a y b cambian respecto de su valor medio en ±5%; sin embargo, estas variaciones solo aplican a la planta, ya que el controlador trabaja con sus valores medios esperados. Esto se muestra matemáticamente en (19).
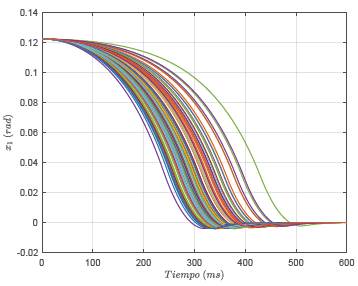
La variación dinámica de la posición y velocidad angular, así como la entrada de control para este escenario son presentadas en las Figuras 10,11 y 12. De este comportamiento dinámico, se puede observar que:
i. La posición y velocidad angular de la barra (ver Figuras 10 y 11) presentan variaciones importantes en los tiempos de estabilización. En el caso de la posición angular, estos tiempos están comprendidos entre los 400 ms y los 550 ms en promedio, mientras que para la velocidad de rotación de la barra están entre los 400 ms y los 600 ms.
ii. En el caso de la ley de control, la saturación de está en ambos extremos se extiende en algunos un poco más de 400 ms en el extremo positivo y hasta un poco más de los 500 ms en el extremo negativo, para luego alcanzar su valor deseado en estado estable, i.e., u ss = 0 en tiempos hasta de 600 ms.
Observación 7 Comparando los resultados de simulación cuando se varían las ganancias de la ley de control y cuando existe incertidumbre paramétrica en las constantes asociadas al RWP, se puede notar que el segundo caso presenta mayores retos para el controlador, ya que los tiempos de estabilización pueden verse aumentados hasta en 100 ms para algunos escenarios de análisis.
Lo anterior puede ser considerado como una posibilidad de investigación futura en la que se consideren directamente las variaciones perimétricas en el diseño del controlador, con el fin de obtener una ley de control robusta que permita minimizar los tiempos de estabilización del sistema, así como ampliar su rango de operación.
6. Conclusiones
En este artículo se presentó un diseño general de control para el RWP basado en una función candidata de Lyapunov, que a través del teorema de estabilidad de Lyapunov, general un controlador no lineal que permite convertir el punto de equilibrio inestable tipo silla del RWP en lazo abierto, en un foco estable durante su operación en lazo cerrado. Además, el diseño de control propuesto es una generalización del método de linealización exacta de las variables de estado o del diseño de control no lineal que considera funciones de energía.
Simulaciones en el software MATLAB con el equivalente discreto del sistema dinámico empleando la derivada hacia adelante, muestran que cuando existen variaciones en las ganancias de la señal de control, los tiempos de estabilización de la planta pueden oscilar entre los 400 ms y los 500 ms; mientras que para el caso de incertidumbre paramétrica en las constantes de la planta, este tiempo de estabilización puede llegar hasta los 600 ms. Adicionalmente, para ambos casos de simulación, debido a las restricciones físicas del sistema simulado, la señal de control presenta saturaciones en sus extremos, lo que indica que se requiere de una estrategia de acercamiento al punto de equilibrio que suavice la entrada en funcionamiento del control propuesto.
Como investigaciones futuras de este trabajo, se recomiendan las siguientes: (i) proponer un diseño de control en tiempo discreto a partir de la metodología de control predictivo que permita optimizar las ganancias de control en función de los requerimientos de la planta y (ii) formular un controlador que considere la incertidumbre parámetrica del sistema el cual pueda ser robusto ante dinámicas no modeladas.
