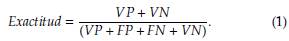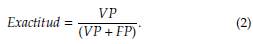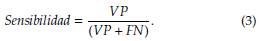1. Introducción

La cantidad de galaxias observadas aumenta exponencial-mente en el tiempo con la llegada de nuevos surveys es-pectroscópicos que permiten estudiar la distribución de la estructura a gran escala: 2dfGRS¹, 6dfGS²,SDSS³ al igual que BOSS⁴ (Baryon Oscillation Spectroscopic Survey; [¹]) y su versión extendida (eBOSS), 4-meter Multi Object Spectroscopy Telescope (4MOST⁵ [²]), DESI⁶ (Dark Energy Spectroscopic Instrument;[³, ⁴], en el futuro Euclid⁷, el Observatorio Vera Rubin (o LSST⁸) y el telescopio espacial Nancy Grace Roman⁹ (o WFIRST) son campañas que están en pleno desarrollo, con su entrada en funcionamiento, nuevos retos se imponen para la clasificación y caracterización de este tipo de espectros. Por ejemplo, en las primeras campañas de BOSS clasificaban los espectros visualmente, lo que implicó para las siguientes campañas corregir errores humanos aleatorios e invertir mucho tiempo para completar correctamente esta tarea.

Haciendo uso de la espectroscopía, que permite estudiar en detalle la trayectoria de la luz emitida por diferentes objetos astrofísicos y su interacción con el medio intergaláctico, en diferentes longitudes de onda. Esta técnica se ha representado a través de los años demostrando que cuando la luz de un objeto pasa a través de un prisma o un dispositivo especial, se divide en diferentes colores, como un arcoíris. Cada color corresponde a una longitud de onda específica. Estos colores nos dan información valiosa sobre la estructura y propiedades de los objetos, como su temperatura, composición química y movimiento propio. Es por eso que en esta investigación la técnica es un principio para clasificar los espectros de cada objeto. Así como lo señala Missey y Hanson [⁵], la espectroscopía se utiliza en muchos campos puesto que es una herramienta poderosa para estudiar la naturaleza de los diferentes objetos.

Un efecto cosmológico importante a tener en cuenta para tratar las líneas espectrales es su desplazamiento con respecto a la longitud de onda en reposo, conocido como redshift (corrimiento al rojo en español). Hay algunas líneas anchas que absorben buena parte del flujo intrínseco emitido por el objeto astrofísico, y por tanto, hacen difícil la clasificación automática de los espectros [⁸]. En el caso de los cuásares podrían presentarse en líneas de absorción anchas,-BAL por sus siglas en inglés; [⁶, ⁷]- o DLA, Damped Lyman Alpha Systems [⁹]. Algoritmos como Quasarnet [¹⁰], SQUEZE (Spectroscopic QUasar Extractor and redshift (z) Estimator) [¹¹,¹²] se diseñaron rutinas de clasificación de espectros de cuásares con resultados muy favorables, dado su enfoque en identificar aquellas líneas que resultan problemáticas para el clasificador (ver por ejemplo el tratamiento mostrado en [¹³]). Estos trabajos se fundamentan en la aplicación de técnicas Convolutional Neural Networks (CNN) y Computer Vision (CV) para la clasificación de objetos astrofísicos que son especialmente útiles si se trabaja, el espectro en formato de imagen como entrada del algoritmo.Dado que para los algoritmos es más sencillo identificar matrices que componen una imagen.

En este trabajo evaluamos el rendimiento de los modelos pre-entrenados para clasificar espectros astrofísicos: INCEPTION V3 [¹⁴], la RESNET 50 [¹⁵] y MNIST [¹⁶], tomados a partir de los resultados de la competencia ILSVRC 14 (ImageNet Large Scale Visual Recognition Challenge) [¹⁷] que utiliza el principio del córtex del ojo humano para identificar patrones de espectros. Este proyecto considera tres métricas de evaluación y diferentes configuraciones de los hiperparámetros del modelo para la consecución de la evaluación.

2. Metodología

En el desarrollo de esta investigación exploratoria se revisa el rendimiento de cada modelo de aprendizaje profundo, aprovechando el entrenamiento previo de cada algoritmo con su respectivo conjunto de datos y sintonizando algunos parámetros para ajustar la entrada a cada modelo como se muestra en la Figura 1.

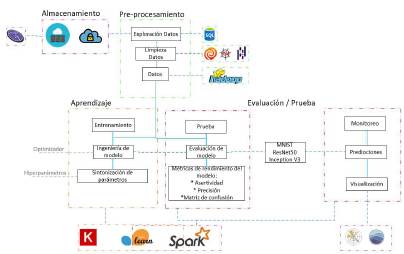
Figura 1: Diagrama representativo de la metodología implementada en este trabajo con cada uno de los algoritmos. 

2.1. Selección de datos

Los espectros utilizados en este trabajo corresponden a datos tomados del espectrógrafo BOSS, en dos versiones: v5_7_0 y v5_7_2¹⁰ que pertenecen al catálogo DR12 de la campaña SDSS. El catálogo seleccionado tiene cerca de 2 millones de objetos astrofísicos. Aplicando la técnica de Muestreo Aleatorio Estratificado (MAE) se recolectó un conjunto de datos de 300000 espectros emitidos por estrellas, cuásares y galaxias, con un redshift entre 0 y 3.5, como se muestra en la Figura 2.

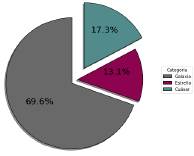
Figura 2: Diagrama circular distribución de clases en la muestra del conjunto de datos completo que corresponde de 300000 espectros. 

Una vez seleccionada la muestra de espectros que se convierten en el conjunto de datos definitivo para aplicar las pruebas, se obtiene una distribución de la cantidad de objetos a través de histogramas como se muestran a continuación en las Figuras 3, 4, 5, correspondientes estrellas, cuásares y galaxias, respectivamente.

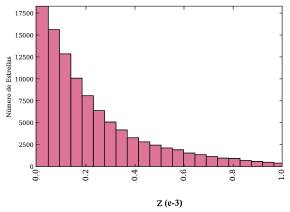
Figura 3: Distribución de estrellas en la muestra como función del redshift. La tendencia de creciente indica que la mayor cantidad de estrellas observadas se encuentran en el vecindario local, dentro o en cercanias a nuestra galaxia, la Vía Láctea, y su brillo es cada vez menos detectado a mayor distancia 

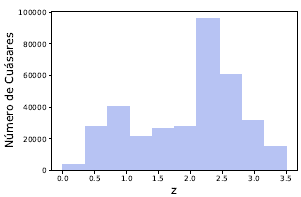
Figura 4: Histograma de cuásares en nuestra muestra con respecto al z observado. El pico de la distribución se encuentra en z~2.4 (cuásares con bosque de Lyman α) de gran interés en cosmología. 

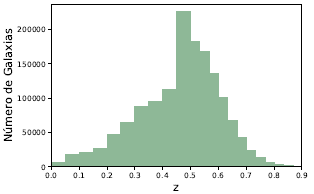
Figura 5: Histograma de galaxias como función de z: la distribución indica una alta cantidad de galaxias en un redshift de 0.5, consistente con los resultados reportados por las diferentes campañas de SDSS. Esta distribución revela que nuestra técnica de selección aleatoria cumple con las condiciones de un muestreo estadístico exitoso 

Aprendizaje

En esta fase de construcción y entrenamiento de los modelos de aprendizaje profundo, el modelo aprende a hacer predicciones y tomar decisiones a partir de los datos de entrada. El proceso se basa en la minimización de una función de costo o pérdida del modelo y los valores reales. También se realizan iteraciones en las que cada modelo ajusta gradualmente sus parámetros e hiperparámetros para reducir el error y mejorar su rendimiento. El éxito del proceso de aprendizaje depende en gran medida de la calidad y cantidad de datos disponibles. Cuanto más sean representativos los datos y mayor sea su diversidad, mejor es la capacidad de clasificación de cada modelo.

Cada algoritmo se entrenó con una proporción de datos diferente en relación a la muestra, evaluadas de la siguiente manera:

• ■ Evaluación 1: con un 60 % de aprendizaje y 40 % de prueba.

• ■ Evaluación 2: con un 70 % de aprendizaje y 30 % de prueba.

• ■ Evaluación 3: con un 80 % de aprendizaje y 20 % de prueba.

Los resultados corresponden a las pruebas ejecutadas con la proporción de la Evaluación 3, porque cada modelo utiliza el conjunto de entrenamiento para ajustar sus parámetros mediante el algoritmo de backpropagation, esto significa que la red aprende a partir de sus errores comparando las salidas con las etiquetas de los datos del entrenamiento.

Tabla 1 Parametrización inicial de cada uno de los algoritmos 

Evaluación

En la fase de prueba se evalúa el rendimiento de los tres algoritmos bajo los siguientes casos:

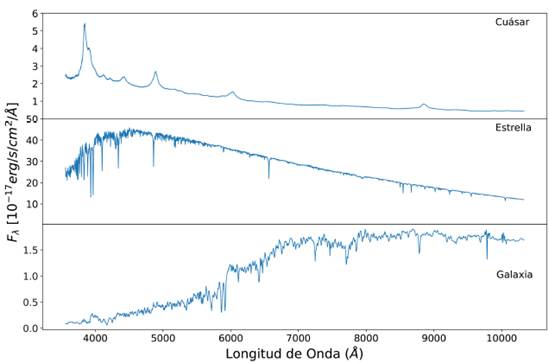
Figura 6: Ejemplos de espectros que se tomaron como entrada para cada uno de los algoritmos. El primer panel corresponde al espectro de un cúasar. El panel central es el espectro de una estrella y finalmente el tercer panel muestra el espectro de una galaxia. Estos rasgos característicos son los que los algoritmos intentan reconocer para realizar la clasificación. 

• ■ Reducción de pérdida por número de épocas.

• ■ Proporción en conjunto de datos con métricas de evaluación: exactitud, precisión y sensibilidad.

En la fase de evaluación de cada algoritmo se tomaron las distribuciones de las evaluaciones 1, 2 y 3 con proporciones de 60/40,70/30 y 80/20, respectivamente. Con cada evaluación se realizaron actualizaciones de ponderaciones con 20, 30 y 40 épocas. Finalmente, se aplicaron las métricas de evaluación a los modelos iterados con 40 épocas. Esta ruta de evaluación para los algoritmos se realiza con el fin de determinar cuál es el comportamiento de cada uno clasificando los espectros. En la fase de evaluación cada modelo se somete a un conjunto de datos por separado que no se utilizó en el entrenamiento, estos datos de prueba son son independientes de los datos utilizados para entrenar cada modelo y proporcionan una medida objetiva del rendimiento.

La clasificación de espectros realizados por los algoritmos se cuantifica con las siguientes categorías:

• ■ Si el espectro corresponde a un objeto determinado y el algoritmo lo clasifica como tal, es un Verdadero Positivo (VP).

• ■ Si el espectro no corresponde al objeto determinado y el algoritmo lo clasifica como cualquiera de las otras clases, es un Verdadero Negativo (VN).

• ■ Si el espectro no corresponde a un objeto determinado y el algoritmo lo clasifica en una clase incorrecta, es un Falso Negativo (FN).

• ■ Si el espectro no corresponde al objeto determinado y el algoritmo lo clasifica como tal, es un Falso Positivo (FP).

Teniendo en cuenta los criterios para la cuantificación, a continuación se definen las métricas de evaluación implementadas:

Exactitud

Esta métrica de evaluación definida en la ecuación (1) busca identificar la frecuencia con la que el algoritmo se equivoca, es decir, reconoce los valores verdadero positivo y verdadero negativo, comparándolos con el total para así determinar, esto arrojaría el resultado de las predicciones correctas, de acuerdo a las proporciones de las clases en el conjunto de datos.

Precisión

La métrica de precisión determina cuantos valores falsos positivos y verdaderos positivos está clasificando el de una categoría, pero que en realidad corresponde a otra distinta. Adicionalmente, con esta métrica es posible determinar si hay un desequilibrio en las proporciones del conjunto de datos, porque al clasificar espectros de objetos que no corresponden a la clase correcta, se incrementa el margen de error del modelo.

Sensibilidad

Esta métrica es también conocida como Recall, busca identificar los espectros clasificados correctamente como positivos dentro del conjunto de positivos verdaderos, tal como se muestra en la ecuación (3):

3. Resultados y discusión

Tomando los 300000 espectros para la clasificación con los algoritmos INCEPTION V3, RESNET 50 y MNIST, los resultados se interpretan partiendo de margen de error y el mejor rendimiento para cada clase.

El margen de error es una variable significativa para determinar la asertividad de la clasificación de los espectros, como lo muestra la Tabla 1 en el valor Error rate, por ello se evaluó cada algoritmo hasta 40 iteraciones, como se muestra en la Figura 7. Además, se ejecutaron las iteraciones con base en la distribución del conjunto de datos correspondiente a la Evaluación 3, tomando el 80 % del conjunto de espectros para la fase de entrenamiento y el 20 % restante para prueba.

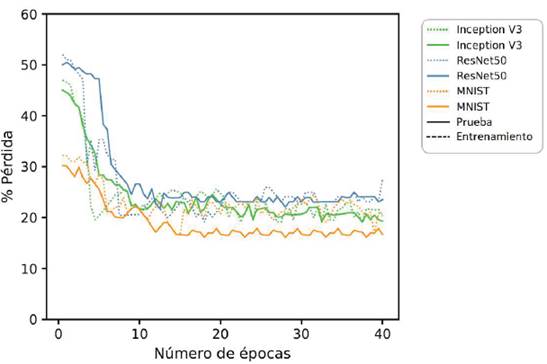
Figura 7: Resultado de las pérdidas por algoritmo evaluado en 40 épocas. Las líneas continuas representan la fase de prueba, mientras que las líneas discontinuas dan cuenta del entrenamiento. 

Los resultados muestran una considerable variación en el porcentaje de pérdida desde cuando los algoritmos se evalúan con 20 épocas hasta cuando se evalúa con 40, progresivamente. Teóricamente, el porcentaje de pérdida debería ser inversamente proporcional al número de épocas, ya que a medida que el número de épocas incrementa el porcentaje de pérdida debe reducirse, como se puede ver en la Figura 7.

Para la evaluación con 20 épocas los resultados muestran que la cantidad de iteraciones no es suficiente para obtener una clasificación confiable, puesto que muestra un leve incremento del error. Asimismo, RESNET 50 es el algoritmo que mayor error arroja cuando se evalúa con el número mínimo de épocas en la fase de entrenamiento. No obstante, la diferencia entre la etapa de prueba y entrenamiento del mismo no presenta diferencias significativas. Es por esto que se evaluaron con más épocas, con el fin de identificar el número de iteraciones con el que cada modelo podría obtener su punto mínimo de error.

En la evaluación con 40 épocas el comportamiento de los algoritmos muestra fluctuaciones moderadas aunque intermitentes, porque en la medida en que crece el número de épocas de evaluación logra regularizar y reducir la tasa de pérdida. Esto demuestra un progreso en el aprendizaje de los modelos, pues que clasifica cada espectro en la clase correcta. Un elemento destacable en el comportamiento de los tres modelos de algoritmo es a causa del número de épocas, dado que cuando superan la iteración 10 presentan una fluctuación más acentuada en la fase de prueba que en la fase de entrenamiento, esto es a causa del progreso en el aprendizaje que cada modelo va teniendo en la medida que las iteraciones incrementan.

El rendimiento de cada modelo se valora considerando los resultados de las métricas exactitud, precisión y sensibilidad como se muestran en las Figuras 10, 9 y 10, por medio de matrices de confusión, que arrojan la cantidad de veces que cada modelo clasifica bien o no un determinado espectro. Además, los resultados de los algoritmos se normalizan con el objetivo de escalar los datos sin distorsionar las diferencias en los intervalos o perder información. En las Figuras 8, 9 y 10 se muestran los resultados por medio de las matrices de confusión, con las clases E, C y G (estrella, cuásar y galaxia, respectivamente). Los resultados están normalizados en un rango entre 0 y 1, indicando el porcentaje de éxito del algoritmo aplicado a cada clase con 40 iteraciones.

La Figura 8 muestra los resultados de la prueba con una distribución de datos del 60 % para entrenamiento y el 40 % para prueba. El análisis de estos resultados se puede interpretar que INCEPTION V3 y RESNET 50 clasifican cuásares en un 80 % mejor que las galaxias con la métrica de exactitud. Además, con la métrica de precisión la clasificación se mantiene en un 80 % para la clase de cuásares, aún con la métrica de sensibilidad se reduce al 70 %. Si se mantuviese esta proporción en el conjunto de datos los mejores clasificadores de cuásares son los modelos INCEPTION V3 y RESNET 50.

Los resultados de la Figura 9 nos llevan a proponer una distribución de mayor proporción para la fase de entrenamiento, puesto que entre más información de entrada tiene cada algoritmo, el modelo reduce su porcentaje de pérdida, como lo muestra la Figura 10. Cambiando la proporción del conjunto de datos, al incrementar 10% en la fase de entrenamiento obtenemos resultados similares a la Evaluación 1 como lo muestra la Figura 9, manteniendo la clasificación de los espectros de cuásar con una bondad del 80 % para los algoritmos RESNET 50 y MNIST; no obstante, INCEPTION V3 reduce en al menos un 15 % de exactitud la clasificación para este mismo tipo de objeto. Además, en la clasificación de espectros de estrellas, ResNet 50 clasifica al 50 % de los espectros de prueba. Por otro lado, para la clasificación de espectros de galaxias ningún modelo muestra un buen desempeño. Esto nos motiva a hacer una tercera evaluación con una distribución para la fase de entrenamiento con un 80 % como se muestra en la Figura 10.

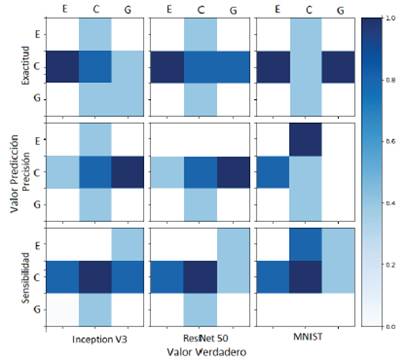
Figura 8: Resultados de balanceo 60/40 de entrenamiento y prueba, respectivamente. En primera fila se evalúa la métrica de exactitud, en la segunda, la de precisión y en la tercera, sensibilidad. De otro lado, la columna a la izquierda muestra los resultados del algoritmo INCEPTION V3, mientras la columna en la mitad, los resultados de RESNET 50 y en la columna a la derecha, MNIST. 

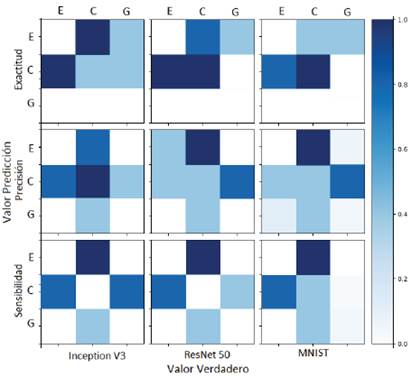
Figura 9: Resultados de balanceo 70/30 de entrenamiento y prueba, respectivamente. De arriba hacia abajo se muestran las métricas de exactitud, precisión y sensibilidad, mientras que de izquierda a derecha se presentan los resultados de los algoritmos INCEPTION V3, RESNET 50 y MNIST. 

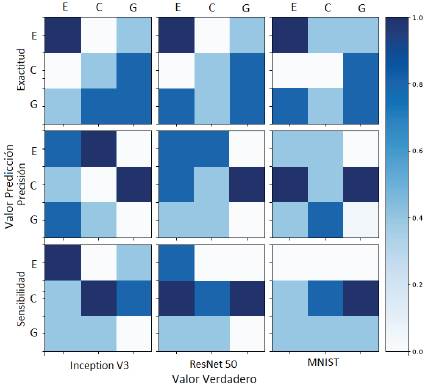
Figura 10: Resultados de balanceo 80/20 de entrenamiento y prueba, respectivamente. En primera fila se evalúa la métrica de exactitud, en la segunda la de precisión y en la tercera sensibilidad. Las columnas muestran los resultados del algoritmo INCEPTION V3, RESNET 50 y MNIST, de izquierda a derecha. 

Los espectros de estrellas y cuásares resultan estar mejor clasificados por el algoritmo RESNET 50, bajo la métrica de precisión, mientras que los espectros de galaxias muestran tener una bajo índice de éxito en la clasificación, con un 10 %.

Para esta evaluación (la número 3, con porcentajes de 80/20 en aprendizaje y entrenamiento), con una mayor proporción de datos de aprendizaje muestra una mejoría en la clasificación ante algunas métricas. Por ejemplo, en la métrica de exactitud la clasificación incrementa en al menos 10 % para cada clase en INCEPTION V3 y RESNET 50. Sin embargo, para MNIST la clasificación se reduce para los cuásares. Esto indica que se pueden implementar los modelos de INCEPTION V3 y RESNET 50 para la clasificación de espectros de estrellas, galaxias y cuásares con estas métricas, con excepción MNIST para la clasificación de cuásares. Para estos casos en los que los algoritmos tienen una fase de pre-entrenamiento, es importante disponer al menos el 80 % del conjunto de datos para re-entrenar cada algoritmo. Durante el desarrollo, los algoritmos pre-entrenados no variaron los pesos predefinidos por los desarrolladores, se conservaron los valores para comparar la tasa de pérdida y de aprendizaje en cada modelo.

En relación al balanceo de las clases, distribuímos el conjunto de datos en dos partes, una para el entrenamiento y el otro para prueba. Sin embargo, en aplicaciones de algoritmos para clasificación se suele dividir en tres, siendo esta última una fase de validación. Para este trabajo tuvimos en cuenta únicamente las dos primeras fases puesto que cada algoritmo trae intrínsecamente un aprendizaje previo adquirido por el conjunto de datos original con el que cada uno fue diseñado y entrenado.

4. Conclusiones

En este trabajo se pusieron a prueba tres algoritmos de Visión Computacional y Redes Neuronales Convolucionales: INCEPTION V3, RESNET 50 y MNIST para clasificar espectros astrofísicos de cuásares, estrellas y galaxias con una muestra de 300000 elementos pertenecientes a la campaña DR12 del cartografiado SDSS. Para evaluar la calidad de la clasificación se consideraron 3 evaluaciones con distinta proporción entre los conjuntos de entrenamiento y prueba, con porcentajes de 60/40, 70/30 y 80/20, respectivamente.

Las métricas de evaluación implementadas demuestran que en el proceso de clasificación, cada modelo reconoce patrones diferentes, esto indica que bajo las pruebas realizadas difícilmente se puede definir a un algoritmo como el mejor clasificador para todas las clases, puesto que el nivel de exactitud varía dependiendo de cada métrica y de cada clase. Dicho esto, podemos inferir que el modelo INCEPTION V3 es mejor clasificador para espectros de estrellas y galaxias con un 85 % y 75 %, respectivamente. También, el algoritmo RESNET 50 clasifica mejor los espectros de estrellas y galaxias con un 83 % y 73 %, respecticamente. Finalmente el modelo de MNIST presenta una clasificación parcial para las tres clases de espectro con un 78 % para estrellas, 22 % para estrellas y 62 % para galaxias, los anteriores resultados fueron obtenidos con una proporción de datos del 20 % para prueba y el 80 % para entrenamiento.

Además de la variación de los parámetros e hiperparámetros en cada algoritmo, la cantidad de iteraciones que se aplica a cada modelo es fundamental para el proceso de aprendizaje, porque en cada iteración representa un incremento en la tasa de aprendizaje de cada modelo.

A lo largo de nuestro estudio se aplicaron los algoritmos pre-entrenados para responder a la clasificación del grupo de espectros, obteniendo resultados concluyentes que demuestran la aplicación de algoritmos de aprendizaje profundo como una excelente herramienta para automatizar la categorización de datos que se obtienen en los telescopios actuales y por tanto, reducir el tiempo que lleva separar, caracterizar y estudiar estos grandes volúmenes de espectros de alta resolución. Los hallazgos encontrados en esta investigación demuestran el impacto que tiene el Machine Learning en el campo de la astrofísica, para lo clasificación de espectros. Incrementando la capacidad de procesamiento eficiente, mejorarando la identificación de patrones complejos, permitiendo a los modelos tener adaptabilidad y aprendizaje contínuo y contribuye a la automatización del proceso de clasificación y a la reducción de los errores humanos.

En futuros trabajos, se considerará hacer una exploración más exhaustiva de los hiperparámetros de los modelos, así como un entrenamiento propio con la optimización de los pesos de los modelos, adaptados a las necesidades de nuestro problema.