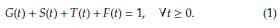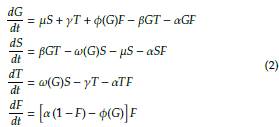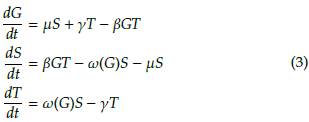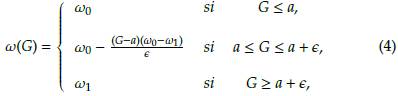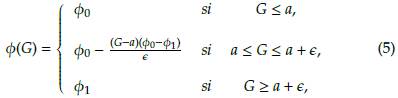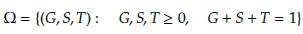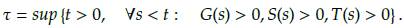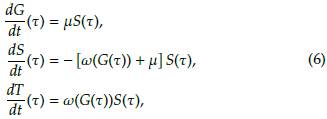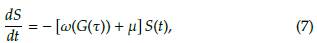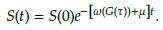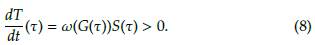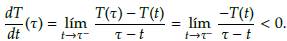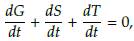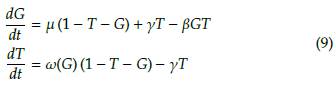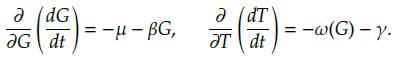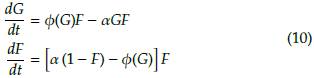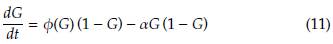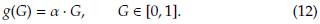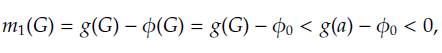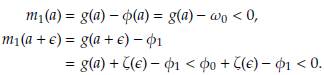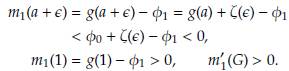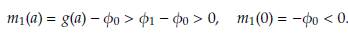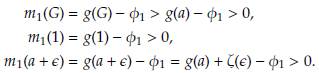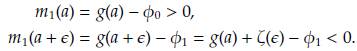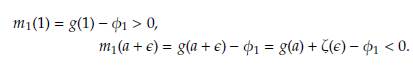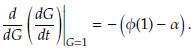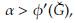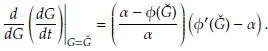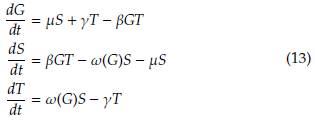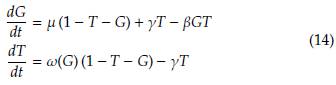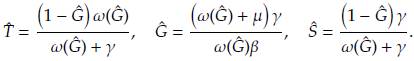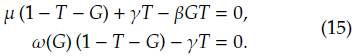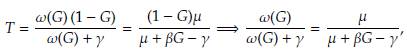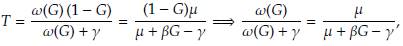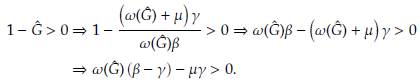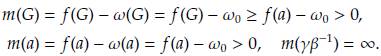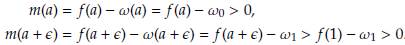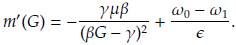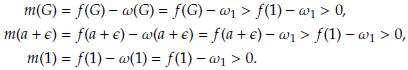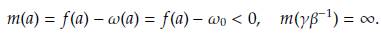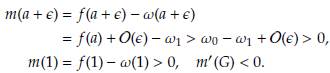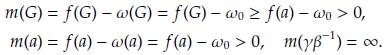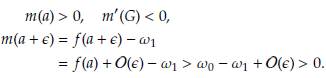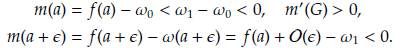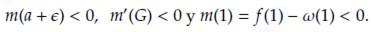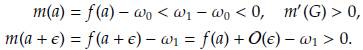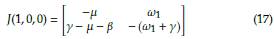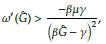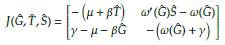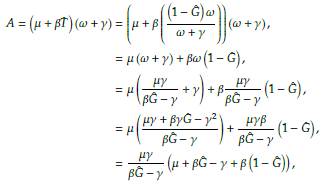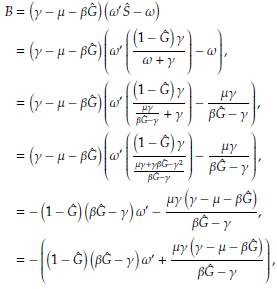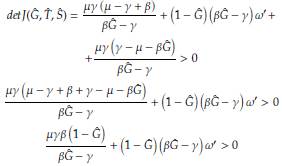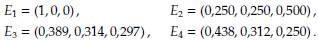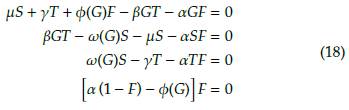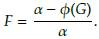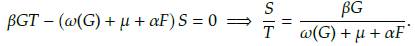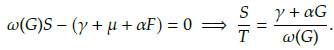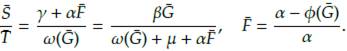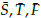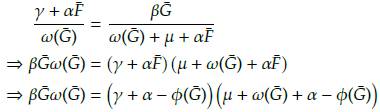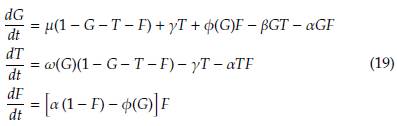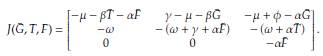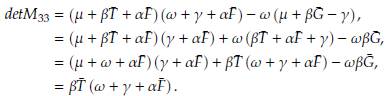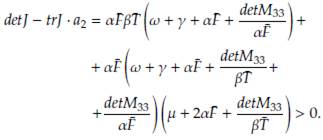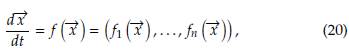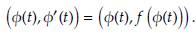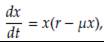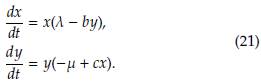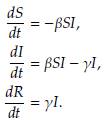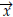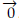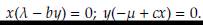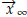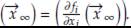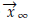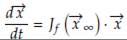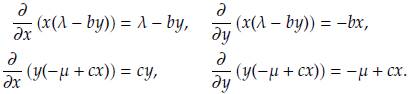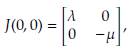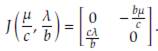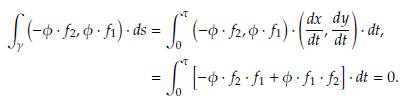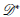2. Algunos conceptos ecológicos

En esta sección presentamos aquellos conceptos de ecología relevantes para el entendimiento del modelo, los cuales fueron tomados primordialmente del libro de Ecología y Medioambiente [⁷].

2.1. Organización ecológica

En ecología, los objetos de estudio se pueden observar en diferentes niveles de jerarquía. Estos niveles de organización, empiezan desde el individuo, especie, población, comunidad, ecosistema, bioma y por último, la biosfera. En este caso, se hablará de las características de los biomas, poniendo un enfoque especial en la sabana y los bosques tropicales (los objetos de estudio de este trabajo).

Bioma, es un sistema ecológico constituido por una gran zona geográfica generalmente ubicada a una cierta latitud. El área que ocupa no se encuentra del todo delimitada, pues más bien un bioma da paso a los adyacentes de forma gradual, sin embargo, su fisionomía nos permite distinguirlos de forma más o menos fácil debido a que presentan una cierta homogeneidad en cuanto a la forma en como están estructurados, su organización y sus patrones de funcionamiento. Entre los principales tipos de biomas conocidos, se encuentran los bosques, las sabanas, los desiertos, las tundras, y los ecosistemas acuáticos epicontinentales, litorales y oceánicos.

Sabana o pastizal, son comunidades caracterizadas por la presencia de pastos que representan las especies dominantes del ecosistema, pues los árboles y arbustos son escasos. Este tipo de bioma se encuentra sobre todo en planicies y mesetas, en regiones que tienen una larga época seca durante el año, donde el clima es desfavorable para los árboles que de otro modo podrían formar bosques. Por lo general, la sabana presenta un clima tropical seco con lluvias en verano, una temperatura promedio anual de alrededor de 20°C y una precipitación promedio de entre 250 y 2000 mm.

Bosque tropical, es un ecosistema con fauna y flora muy diversas, cada especie con frecuencia presenta una población no tan numerosa, pero si muy diseminada, por lo que no suele existir una clara especie dominante. La mayoría de los bosques tropicales se ubican a baja altitud y cercanas a la costa. Su clima suele ser cálido húmedo, con temperaturas promedio cercanas a los 27° C que no varían prácticamente con las estaciones o con la noche. La precipitación suele ser abundante y equitativamente repartida en todos los meses del año, por lo regular de más de 1000 mm anuales, aunque en algunas áreas del amazonas o del sureste de Asia puede superar los 4000 mm por año.

Sucesión ecológica, es la variación temporal no estacional de la diversidad de especies que constituyen a una comunidad. Para que una sucesión ecológica tenga lugar es necesaria la existencia de un disturbio que afecte e incluso elimine a los organismos de la comunidad, dejando espacios abiertos a la colonización de nuevos organismos.

2.2. Estabilidad ecológica

El término estabilidad, en el contexto ecológico es multifacético. Dicho concepto puede referirse a la persistencia que tiene un ecosistema para preservar su estado a través del tiempo, esto quiere decir que un ecosistema que perdure durante más tiempo, será más estable. Por otra parte, también se puede hablar de estabilidad en términos de perturbación, esto es, si un ecosistema retorna a un estado de equilibrio después de perturbado entonces se dice que dicho ecosistema es estable, sin importar la magnitud de la perturbación [¹³, ⁹]. Esta última definición es equivalente a la estabilidad asintótica que se maneja en los modelos dinámicos en matemáticas, cuya definición se discute en el apéndice.

La estabilidad es un concepto que puede tener varias clasificaciones, dependiendo de la magnitud de la perturbación o de acuerdo a la coexistencia de más de un estado estable. A continuación se presentan algunas de estas clasificaciones.

Estabilidad local y global. Se dice que un sistema posee estabilidad local cuando es estable sobre pequeñas perturbaciones de corta duración, mientras que la estabilidad global se refiere a un sistema altamente resistente al cambio en la composición de especies y/o la dinámica de la red alimentaria.

Estados estables alternativos. Un sistema posee estados estables alternativos si bajo las mismas condiciones externas (carga de nutrientes, temperatura, entre otras) puede establecerse en diferentes estados estables. Este nombre esta reservado especialmente cuando se trabaja con modelos [⁸].

3. Modelo de Staver y Levin

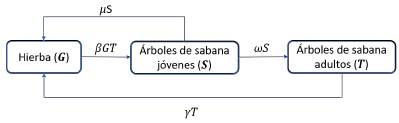
El modelo del cual hablaremos en esta sección es el propuesto por Staver y Levin en [¹⁵], el cual busca establecer la dinámica entre los biomas de sabana y bosques, reduciendo la población vegetal a árboles de bosque (F), árboles de sabana (T), árboles jóvenes de sabana (S) y pastos (G), bajo los efectos típicos del fuego, la lluvia y la competencia por el espacio (ver Figura 1). El modelo en cuestión es temporal, debido a que no es espacialmente explícito pues todo el espacio se contabiliza implícitamente teniendo en cuenta que es ocupado por G, S, T o F en todo instante de tiempo, es decir,

3.1. Descripción del modelo

Los supuestos del modelo son:

1. El fuego genera disturbios en los ecosistemas, produce un proceso de sucesión ecológica, por tal motivo, se observa una jerarquización forestal en donde, la hierba se planta inicialmente, posteriormente llegan al lugar los árboles jóvenes y por último se establecen los árboles adultos.

2. La hierba dificulta la formación de árboles adultos al retrasar el reclutamiento de árboles jóvenes a adultos.

3. Los árboles jóvenes de sabana son producidos por los árboles adultos de sabana en proporción a la densidad de árboles.

4. Al morir los árboles (tanto de sabana como de bosque) son reemplazados por la hierba.

Figura 1: Diagrama de flujo del modelo (Adaptación de figura en [¹⁵]). 

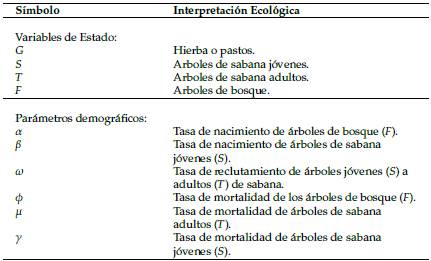
Con lo antes expuesto se presenta a continuación el sistema de ecuaciones que representa el modelo de Staver y Levin, además, en la Tabla 1, se presentan las variables de estado y demográficas del modelo asi como su interpretación ecológica.

Los árboles jóvenes de sabana se establecen en espacio ocupado sólo por pasto y en proporción al número de árboles adultos de sabana presentes en el sistema (tasa constante β). El reclutamiento de árboles de sabana jóvenes a adultos se da a una tasa ω(G) en proporción a la cantidad de árboles jóvenes de sabana disponibles. Cuando mueren los árboles dicho espacio es ocupado por el pasto de acuerdo a la cantidad de árboles en el sistema (tasas μ, y y φ(G)). Los árboles de bosque se establecen en espacios ocupados por hierba y árboles de sabana en proporción a la cantidad de dichos árboles disponibles (tasa constante α).

Tabla 1: Parámetros y variables del modelo. 

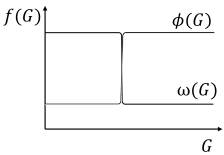
El modelo incorpora dos suposiciones fundamentales sobre la ecología de la sabana. Primero, se asume que la propagación del fuego en la sabana depende de la abundancia del pasto, como se refleja en la función ω(G) y φ(G). La sabana con una cobertura arbórea por debajo del 40 % se quema con frecuencia, pero el fuego es casi inexistente en los sistemas con cobertura arbórea por encima del umbral del 40 %. Se incorpora esta respuesta no lineal de frecuencia de incendios a la abundancia de pasto a través de ω(G), el reclutamiento de plántulas en árboles. El fuego rara vez mata a los árboles jóvenes de la sabana, que pueden rebrotar después del fuego, y rara vez afecta a los árboles adultos. El fuego impone un control importante sobre el reclutamiento de árboles jóvenes a adultos. Estas características de los sistemas de sabana significan que el reclutamiento de árboles debe ser alto cuando la abundancia de pastos (y la frecuencia de incendios) es baja, debe disminuir rápidamente cerca del 40 % de la cubierta de árboles y debe permanecer baja en abundancia de hierba alta [¹⁴].

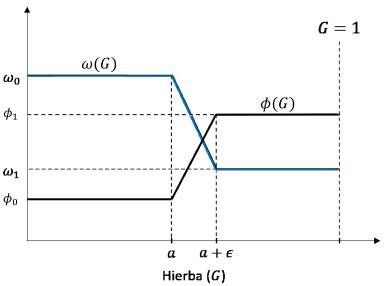
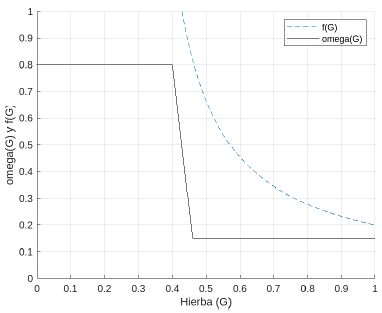
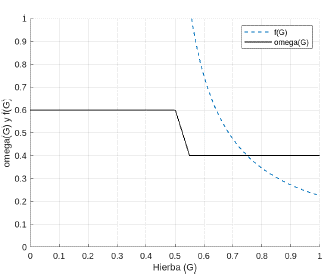
Por otra parte, la ecología del bosque es diferente a la sabana. La propagación del fuego ejerce un limitante para los árboles, afectando directamente su tasa de mortalidad φ(G). En este caso igualmente se asume que la propagación del fuego en el bosque depende de la abundancia del pasto. Es decir, la mortalidad de los árboles de bosque intrínseca (causas ajenas a los incendios) debería ocurrir cuando la abundancia de pasto está por debajo del 40 % y que la mortalidad inducida por el fuego debe ocurrir cuando la abundancia del pasto sea alta [¹⁵]. En este caso, se asume que ω(G) y φ(G) son funciones suaves y poseen forma sigmoidal. La tasa de reclutamiento de árboles jóvenes a adultos de la Sabana (ω) junto con la tasa de mortalidad de los árboles de bosque (φ) están condicionadas por la propagación del fuego y las condiciones climáticas, por tanto, indirectamente serán variables que dependerán de la disponibilidad de G (Figura 2).

Figura 2: Gráfica de las funciones c(G) y 0(G) (Adaptación de figura en [¹⁵]). 

3.2. Algunos resultados del trabajo de Brhane

Figura 3: Diagrama de flujo del modelo (Adaptación de figuras en [¹⁴] y [²]. 

En esta sección se presentan algunos resultados encontrados por Brhane en [²]. El modelo estudiado es el planteado en [¹⁴] y [¹⁵], sin embargo, se hace una simplicación al no incluir los árboles de bosque, es decir, esta enfocado sólo en el bioma de sabana (ver Figura 3). De acuerdo a lo anterior, el modelo simplificado es el siguiente

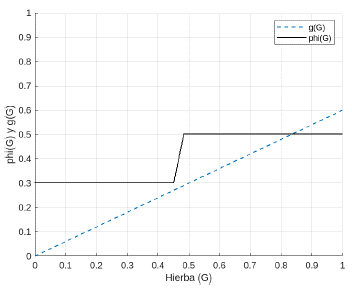
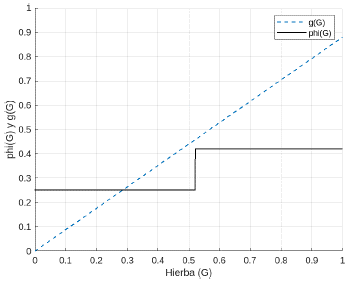
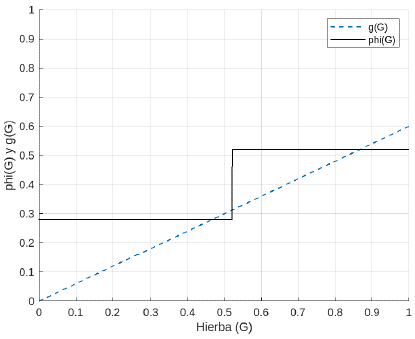
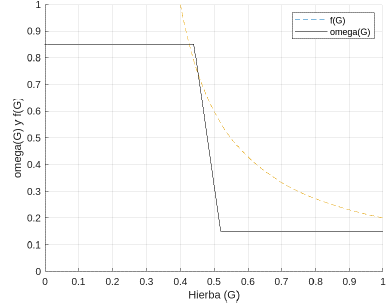
Adicionalmente, se hace un cambio en la concepción de la función ω (ver Figura 4), pues tiene una discontinuidad de salto. Por tanto, en este trabajo se propuso definirla como una función a trozos (ver Figura 4) la cual se presenta a continuación

donde ω₀ > ω₁ > 0 y 0 < α < 1, además, e es un número suficientemente pequeño mayor que cero. Igualmente, se propone para trabajos futuros cambiar la función 0 (ver Figura 4), como se describe a continuación

donde 0₁ > φ₀ > 0 y 0 < a < 1, además, ∈ es un número suficientemente pequeño mayor que cero.

Figura 4: Representación de las función ω(G) y φ(G) (Adaptación de figura en [²]). 

En este caso el dominio de definición de las soluciones será el conjunto

Tenemos el siguiente resultado

Teorema 1. Todas las soluciones del sistema con condición inicial positiva son no negativas para todo tiempo t ≥ 0.

Demostración. Por hipótesis tenemos que

G(0) > 0, S(0) > 0 y T(0) > 0. Definimos t ∈ ℝ tal que,

Note que si t = ∞ entonces el teorema está probado. Por tanto, procederemos por contradicción, suponiendo que 0 < t < ∞. Se tendrán tres posibilidades, G(t) = 0, S(t) = 0 ó T(t) = 0. Sin perdida de generalidad supongamos que T(t) = 0, evaluando en t en el sistema (3) y reduciendo se obtiene

y debemos anotar que estas ecuaciones se satisfacen puntualmente. Supongamos que la segunda ecuación se cumple para todo instante de tiempo t, en particular, se cumplirá para t = t. Así mismo, se supone que ω(G(t)) es constante. Por tanto, se tendrá la siguiente ecuación diferencial de primer orden

La ecuación (7) es denominada de crecimiento exponencial o modelo de Malthus cuya solución será

Ahora, evaluando en t = t, obtenemos S(t) = S(0)e^{-[ω(G(T))+p]T} > 0. Tomando la tercera ecuación del sistema (6) se obtiene que

Por otra parte, notese que

Lo anterior, contradice el resultado obtenido en (8), en consecuencia, se tiene que T(t) > 0 para todo t ≥ 0. De la misma manera como se procedió aquí, se puede probar que G(t) > 0, ∀t > 0 (ver [2]) y S(t) > 0, ∀t ≥ 0. Con lo cual se concluye la prueba.

Corolario 1. El conjunto Ω es positivamente invariante.

Demostración. Supongamos que (G(0), S(0), T(0)) ∈ Ω, es decir,

G(0) > 0, S(0) > 0, T(0) > 0 y además G(0) + S(0) + T(0) = 1.

Note que sumando el sistema de ecuaciones de (3) se obtiene

e integrando con respecto a t obtenemos G(t) + S(t) + T(t) = c, donde c es la constante de integración. Note que por la condición inicial se tiene que c = 1. Es decir obtenemos que, G(t) + S(t) + T(t) = 1. Por último, por el teorema demostrado previamente se tiene que las soluciones serán no negativas siempre que t ≥ 0. En consecuencia, cualquier solución con t ≥ 0 cumple las condiciones para pertenecer a Ω.

Para reducir la complejidad del sistema (3), se puede utilizar la condición espacial, S(t) = 1 - G(t) - T(t) para todo instante de tiempo t > 0, con lo cual se obtiene un sistema de dos ecuaciones ordinarias no lineales como se muestra a continuación,

Teorema 2. El sistema de ecuaciones diferenciales no posee soluciones periódicas en Ω.

Demostración. En este caso, el conjunto solución Ω es simplemente conexo (pues, geométricamente es la porción de un plano limitado en el primer octante). Por otra parte,

Tomando φ(G, T) = 1, entonces 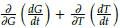no cambia de signo por lo menos en Ω. En consecuencia, usando el criterio de Dulac (Teorema 10) se concluye que el sistema no posee soluciones periódicas en Ω.

4. Coexistencia de hierba (G) y árboles de bosque (F)

Esta sección la dedicamos al estudio de un caso particular del modelo de Staver y Levin [¹⁵], en donde se conocerán las soluciones de equilibrio del sistema con la ausencia de los árboles de Sabana (S y T), mirando la dinámica poblacional que puede ocurrir entre la hierba (G) y los árboles de bosque (F) (ver Figura 5). Adicionalmente, se tomará la función 0 tal como lo sugiere Brhane [²] (ver ecuación (5) y Figura 4). En este caso el sistema a estudiar es

Figura 5: Diagrama de flujo del modelo (Adaptación de figura en [¹⁵]). 

4.1. Soluciones de equilibrio

Elsistema(10)seanulasiemprequeF = 0yG = 1,esteeselequilibrio trivial del sistema. Ahora, supongamos que los árboles de bosque y la hierba coexisten simultáneamente (esto es F > 0 ); en este caso, por la condicional espacial se puede reducir el sistema (10) de la siguiente manera

Proposición 1. Las soluciones de equilibrio no triviales del sistema (10) se obtienen cuando

Demostración. Note que (11) se anula siempre que φ(G) = αG. El resultado es inmediato despejando la variable 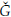de la condición anterior, posteriormente usando la condición espacial se determina .

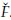Elequilibriotrivialsiempreesadmisible.Porotraparte,lassoluciones de equilibrio no triviales serán admisibles siempre que la tasa de nacimientos de árboles de bosque sea superior a la tasa de mortalidad de árboles de bosque, es decir, α > φ. En efecto, si ocurriese lo contrario, el sistema evoluciona a un estado donde solo existe hierba (G).

Definiendo una función g que depende de G tal que,

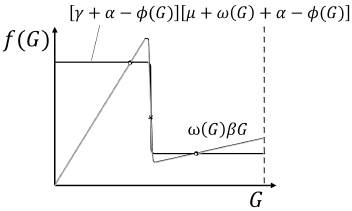
Se puede inferir por medio de lo anterior que toda solución de equilibrio del sistema debe satisfacer que φ(G) = g(G). Así mismo, las soluciones de equilibrio son raíces de la función definida como

donde la función m ₁ representa la tasa de variación de los árboles de bosque. Bajo ciertas condiciones que deben satisfacer los parámetros demográficos, se puede garantizar la existencia de un máximo de cuatro soluciones de equilibrio. El siguiente resultado nos da razón de las condiciones para encontrar los equilibrios no triviales y la cuantía de estos.

Lema 1. Suponga que g(1) > φ₁ y ∈ > 0 suficientemente pequeño

1. S i g(a) < φ₀ entonces existe una solución de equilibrio no trivial (Ğ) para el sistema (10) tal que a + ∈ < Ğ<a

2. S i g(a) > 01 entonces existe una solución de equilibrio no trivial (Ğ, 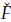) para el sistema (10) tal que 0 < Ğ < a.

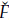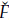3. Si φ₀ < g(a) < φ₁ entonces existen soluciones de equilibrio no triviales (Ğ ₁ , , (Ğ ₂, ₂) y (Ğ ₃, 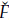₃) para el sistema (10) tal que 0 < Ğ ₁ < a, a < Ğ ₂ < a + ∈ ya + ∈< Ğ ₃ < 1.

Demostración. En primer lugar, caractericemos la función m1(G). La derivada de dicha función es m1 (G) = a - 0'(G). Note que m1 (G) > 0 siempre que 0 < G < a ó a + ∈ < G < 1, mientras que será negativa si a < G < a+∈. Lo anterior garantiza que dicha función es estrictamente decreciente o creciente en alguno de los tres intervalos.

Consideremos el intervalo 0 < G < a para el cual tenemos

Entonces, la función m ₁ no posee raíces para 0 < G < a. En consecuencia, no existe solución de equilibrio en dicho intervalo. Ahora, consideremos el intervalo a < G < a + e

Por lo anterior y teniendo en cuenta que la función m ₁ posee comportamiento estrictamente monótono, dicha función no posee raíces para a < G < a + e. En consecuencia, no existe solución de equilibrio en dicho intervalo. Finalmente, para este caso consideremos el intervalo a + ∈ ≤ G ≤ 1. Entonces,

Por el Teorema de Bolzano, la función m ₁ posee raíces para a+ ∈ < G < 1. La unicidad de dicha raíz se garantiza debido al comportamiento monótono de la función. En consecuencia, existe una única solución de equilibrio en dicho intervalo.

2. Considere el intervalo 0 ≤ G ≤ a.

Por el Teorema de Bolzano, la función m ₁ posee raíces para 0 < G < a. La unicidad de dicha raíz se garantiza debido al comportamiento monótono de la función. En consecuencia, existe una única solución de equilibrio en dicho intervalo. Ahora, considere el intervalo a < G < a + ∈, entonces m₁ (G) = g(G) - φ(G) > g(a) - φ (G) > φ ₁ - φ (G) > 0. Esto prueba que la función m ₁ no posee raíces en el intervalo a < G < a + ∈. Por último considere el intervalo a + ∈ < G < 1, entonces

Por lo anterior la función m1 no posee raíces para a+∈ < G < 1. En consecuencia tampoco existe solución de equilibrio en este intervalo.

3. Considere el intervalo 0 ≤ G ≤ a, entonces m₁(a) = g(a)-φ₀ > 0, m₁(0) = -φ0 < 0. Por el Teorema de Bolzano, la función m ₁ posee raíces para 0 < G < a. La unicidad de dicha raíz se garantiza debido al comportamiento monótono de la función. En consecuencia, existe una única solución de equilibrio en dicho intervalo. Ahora, considere el intervalo a < G < a + ∈, tenemos

Por el Teorema de Bolzano, la función m ₁ posee raíces para a < G < a + ∈. La unicidad de dicha raíz se garantiza por la monoticidad de la función. En consecuencia, existe una única solución de equilibrio en dicho intervalo. Por último considere el intervalo a + ∈ ≤ G ≤ 1, entonces

Figura 6: Existencia de soluciones de equilibrio para el caso (a) del Lema 1. 

Por el Teorema de Bolzano, la función «74 posee raíces para a+∈ < G < 1. La unicidad de dicha raíz se garantiza debido al comportamiento monótono de la función. En consecuencia, existe una única solución de equilibrio en dicho intervalo.

A continuación presentamos algunos ejemplos donde se evidencia la existencia de las soluciones de equilibrio no triviales de acuerdo al lema 1.

Ejemplo 1. Considere los siguientes valores para los parámetros demográficos, a = 0,6, φ₀ = 0,3, φ ₁ = 0,5, a = 0,45, ∈ = 0,033.

Con estos valores se obtiene g(1) = 0,6 > 0,5 = 01 y además, g(a) = 0,27 < 0,3 = φ₀. En consecuencia se cumple el primer caso del lema anterior, por tanto, existe una solución de equilibrio tal como lo muestra la figura 6.

Ejemplo 2. Considere los siguientes valores para los parámetros demográficos, a = 0,88, 0₀ = 0,25,0₁ = 0,42, a = 0,52, ∈ = 0,001.

Con estos valores se obtiene que g(1) = 0,88 > 0,42 = φ1 y además, g(a) = 0,45 < 0,42 = φ₁. En consecuencia se cumple el segundo caso del lema anterior, por tanto, existe una solución de equilibrio tal como lo muestra la figura 7.

Figura 7: Existencia de soluciones de equilibrio para el caso (b) del Lema 1. 

Ejemplo 3. Considere los siguientes valores para los parámetros demográficos, α = 0,6, φ₀ = 0,28,φ₁ = 0,52, a = 0,52, ∈ = 0,001.

Al utilizar los valores de este ejemplo se obtiene que g(1) = 0,6 > 0,52 = φ₁ y además, φ₀ = 0,28 < g(a) = 0,45 < 0,42 = φ₁. En consecuencia se cumple el tercer caso del lema anterior, por tanto, existen tres soluciones de equilibrio tal como lo muestra la figura 8.

Figura 8: Existencia de soluciones de equilibrio para el caso (c) del Lema 1. 

4.2. Análisis de estabilidad

En esta sección presentamos una condición que garantiza que las soluciones halladas en la sección anterior sean asintóticamente estables. En primera instancia, miremos un resultado relacionado con la estabilidad de la solución de equilibrio trivial.

Lema 2. La solución de equilibrio (1,0) del sistema (10) es asintóticamente estable siempre que g(1) < φ₁. Por el contrario, si g(1) > φ₁ entonces el equilibrio (1,0) es inestable.

Demostración. Derivando la ecuación (11) con respecto a G y evaluando en G = 1 se obtiene que,

Por el Teorema 5 (Apéndice), el sistema es asintóticamente estable si la derivada presentada previamente es negativa, lo cual ocurre siempre que α < φ(1).

Proposición 2. Cualquier solución de equilibrio (Ğ, 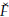) del sistema (10) es asintóticamente estable siempre que,

donde el lado derecho de la expresión es la derivada del parámetro φ.

Demostración. Derivando la ecuación (11) con respecto a G y evaluando en G = Ğ se obtiene

Por el Teorema 5, el sistema es asintóticamente estable si la derivada presentada previamente es negativa, lo cual ocurre siempre que φ'(Ğ) < α.

El siguiente resultado es una consecuencia inmediata de la Proposición 2.

Corolario 2. Suponga que g(1) > ϕ ₁ y ∈ > 0 suficientemente pequeño

1. Toda solución de equilibrio no trivial G del modelo (10) tal que 0 < G < a ó a + ∈< G < 1 es asintóticamente estable.

2. Toda solución de equilibrio no trivial G del modelo (10) tal que a < G < a + ∈ es inestable.

Ejemplo 4. Considere los siguientes valores para los parámetros demográ-jicos, α = 0,5, φ₀ = 0,4,φ₁ = 0,8, a = 0,45, ∈ = 0,033.

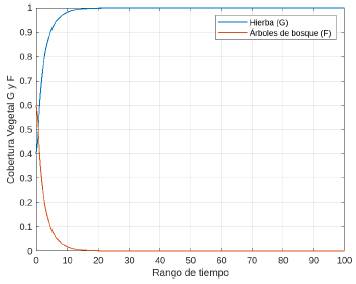
Con estos valores se obtiene que g(1) = a = 0,5 < 0,8 = ϕ ₁. En consecuencia, el sistema no admite soluciones de equilibrio no triviales, entonces la única solución de equilibrio será E1 = (0,1). Por el Lema 2, se puede aseverar que la solución de equilibrio E1 es estable. Para analizar la estabilidad del equilibrio E1, se toma el valor inicial (G(0), F(0)) = (0,20,0,80). Como se observa en la Figura 9, el sistema evoluciona rápidamente a la solución de equilibrio trivial.

Figura 9: Dinámica del sistema para la condición inicial (G, F) = (0,80, 0,20). 

Ejemplo 5. Considere los parámetros demográficos del ejemplo 3

De acuerdo a lo expuesto en la sección pasada, en especial el lema 1, existen cuatro soluciones de equilibrio E1 = (1,0), E₂ = (0,4667, 0,5333) ,

E₃ = (0,5201,0,4799), and E₄ = (0,8667,0,1333). Por el Lema 2 y el Corolario 2, se tiene que E ₂ y E ₄ son asintóticamente estables, mientras que E1 y E₃ son inestables. Si se toma el valor inicial (G(0), F(0)) = (0,35,0,65), el sistema evoluciona rápidamente al equilibrio E ₁ , como se muestra en la Figura 10.

Figura 10: Dinámica del sistema para la condición inicial (G, F) = (0,35, 0,65). 

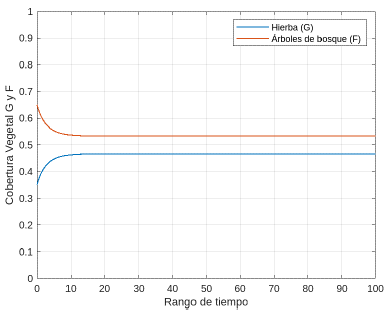
Para estudiar la estabilidad del equilibrio E ₄ , se toma como valor inicial (G(0), F(0)) = (0,55,0,45). En este caso, como se observa en la Figura 11, el sistema evoluciona rápidamente a este equilibrio. De esta simulación se puede asegurar que coexisten para el sistema dos equilibrios simultáneamente estables.

Figura 11: Dinámica del sistema para la condición inicial (G, F) = (0,55, 0,45). 

Para el caso donde se presenta ausencia del fuego, el sistema tiende a evolucionar a un estado donde predominan los árboles de bosque (en este caso se habla del equilibrio E₂). Por otra parte, cuando hay mayor incidencia de incendios, como es de esperar, la hierba se vuelve dominante (para este caso se habla del equilibrio E4), debido a que el fuego ejerce un limitante para los árboles de bosque.

5. Coexistencia de Hierba (G) y árboles de Sabana (S y T)

Esta sección está enfocada en encontrar las soluciones de equilibrio del sistema con la ausencia de los árboles de bosque (F), mirando los equilibrios y la dinámica que puede ocurrir entre la hierba y los árboles de sabana. En este caso el sistema que se estudiará es

5.1. Soluciones de equilibrio

Dentro de los equilibrios del sistema, podemos encontrar que existe un equilibrio trivial cuando todo el espacio está ocupado por hierba, esto es, G = 1 y S = T = 0. Ahora, supongamos que los árboles de sabana y la hierba coexisten simultáneamente (esto es, S > 0, T > 0). Por la ausencia de bosque y teniendo en cuenta que S = 1 - G - T, obtenemos la siguiente reducción del sistema (13),

Proposición 3. Las soluciones de equilibrio no triviales (Ĝ,Ŝ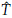) del sistema (14) satisfacen que

Demostración. Por la definición de solución de equilibrio, se obtiene el siguiente sistema de ecuaciones

Despejando T de la primera ecuación de (15) obtenemos T = j 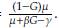Así mismo, despejando la misma variable de la segunda ecuación de (15)obtenemos T = 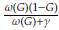igualando los resultados hallados previamente tenemos

Despejando la variable G obtenemos G =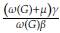. Por último, para determinar la expresión faltante para S basta con utilizar la condición S = 1 - G - T y reemplazar la expresión hallada para la variable T.

Lema 3. Las soluciones de equilibrio no triviales del sistema (14 son admisibles siempre que «(Ĝ) (β − γ) > γμ.

Demostración. Para que (Ĝ Ŝ 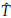)sea una solución de equilibrio no trivial, se debe garantizar que Ŝ, 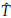> 0, lo cual se cumple siempre que 1 - Ĝ > 0, por tanto

Las soluciones de equilibrio no triviales deben satisfacer las ecuaciones propuestas en 3, sin embargo, basta con que se cumpla la ecuación para la variable G, pues las demás variables dependen de ésta. Despejando de la condición para G el parámetro ω obtenemos ω(Ĝ): 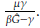Definimos la función f que depende de G tal que

con dominio (γβ ^-1,1]. De esto se puede inferir que toda solución de equilibrio del sistema debe satisfacer que ω(G) = f (G). Por otra parte, las soluciones de equilibrio son raíces de la función definida como m(G) = f (G) - ω (G).

Aparte de la condición descrita en el Lema 3, las soluciones de equilibrio no triviales existen siempre y cuando γβ ^-1 < 1, lo cual es equivalente a β > γ. En otras palabras, las soluciones de equilibrio no trivial son admisibles siempre y cuando la tasa de natalidad de árboles de sabana jóvenes (S) supere la tasa de mortalidad de árboles de sabana jóvenes (S). En efecto, si ocurriese lo contrario, el sistema evoluciona al estado donde solo existe hierba (G).

De acuerdo a las ecuaciones de la Proposición 3 que debe satisfacer todo equilibrio no trivial, se pueden encontrar un máximo de cuatro soluciones de equilibrio (una de ellas es la trivial). Los dos siguientes resultados nos dan razón sobre las condiciones que deben satisfacer los parámetros para garantizar la existencia de las soluciones de equilibrio y su cuantía.

Lema 4. Suponga que f (1) > ω₁ y ∈ > 0 suficientemente pequeño,

(a) Si f(a) > ω₀ entonces no existen soluciones de equilibrio no triviales para el sistema (3).

(b) Si f(a) < ω₀ entonces existen dos soluciones de equilibrio no triviales (Ĝ ₁, Ŝ ₁, 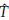₁) y (Ĝ ₂ , Ŝ ₂, 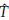₂) del sistema (3) con γβ ^-1 < Ĝ ₁ < a y a < Ĝ ₂ < a + ∈.

Demostración. La función f como se definió en la ecuación (16) es estrictamente decreciente, debido a que su derivada siempre es negativa. Además, dicha función es continua en su dominio de definición, lo cual induce que m también lo sea.

(a) Considere el intervalo γβ ^-1 < G ≤ a.

Por lo anterior la función m no posee raíces para γβ ^-1 < G ≤ a. En consecuencia no existe solución de equilibrio en dicho intervalo.

Ahora, considere el intervalo a < G < a + ∈, entonces

La derivada de la función m es

Por tanto, tenemos que m’ (G) > 0 en a < G < a + ∈, debido a que e es suficientemente pequeño. Por lo anterior la función m no posee raíces para a < G < a + ∈. En consecuencia no existe solución de equilibrio en dicho intervalo.

Por último considere el intervalo a + ∈ < G < 1

Por lo anterior la función m no posee raíces para a + ∈ < G < 1. En consecuencia no existe solución de equilibrio en dicho intervalo. En conclusión no existen soluciones de equilibrio no triviales con las condiciones dadas.

(b) Considere el intervalo γβ ^-1 < G ≤ a

Note que para G ∈ (γβ ^-1, a] U [a + ∈, 1] la derivada de m será m’ (G) = 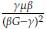debido a que la función «(G) es constante. En consecuencia, m’ (G) < 0. Esto prueba que la función m posee raíces en el intervalo γβ ^-1 < G ≤ a, es decir que existe solución de equilibrio en dicho intervalo.

Ahora, considere el intervalo a ≤ G ≤ a + ∈.

Lo anterior prueba que la función m posee raíces en el intervalo a < G < a + e. En consecuencia existe solución de equilibrio en dicho intervalo.

Por último considere el intervalo a + e ≤ G ≤ 1.

Por lo anterior la función m no posee raíces para a+ ∈ < G < 1, es decir no existe solución de equilibrio en dicho intervalo.

En conclusión, existen dos soluciones G₁ y G₂ tal que γβ ^-1 < G1 < a y a < G₂ < a + ∈ con las condiciones dadas.

Ejemplo 6. Considere los siguientes valores para los parámetros demográficos, j = 0,5, y = 0,2, β = 0,7, ω₀ = 0,8, ω1 = 0,15, a = 0,4, e = 0,06. Con estos valores se obtiene que f (1) = 0,2 > 0,15 = ω₁ y además, f (a) = 1,25 > 0,8 = ω₀. En consecuencia se cumple el primer caso del lema anterior, por tanto, no existen soluciones de equilibrio tal como lo muestra laFigura 12.

Figura 12: Existencia de soluciones de equilibrio para el caso (a) del Lema 4. 

Ejemplo 7. Considere los siguientes valores para los parámetros demográficos, j = 0,6, γ = 0,2, β = 0,8, ω0 = 0,85, ω1 = 0,15, a = 0,44, ∈ = 0,06. Con estos valores se obtiene que f (1) = 0,2 > 0,15 = ω₁ y además, f (a) = 0,79 < 0,85 = ω₀. En consecuencia se cumple el segundo caso del lema anterior, por tanto, existen dos soluciones de equilibrio no triviales, tal como lo muestra laFigura 13.

Figura 13: Existencia de soluciones de equilibrio para el caso (b) del Lema 4. 

Lema 5. Suponga que f (1) < ω₁ y ∈ > 0 suficientemente pequeño,

(a) S i f (a) > ω₀ entonces existe una solución de equilibrio no trivial (Ĝ, Ŝ, 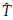para el sistema (3) tal que a + ∈ < G < 1.

(b) S i f (a) < ω₁ entonces existe una solución de equilibrio no trivial (Ĝ, Ŝ, 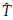para el sistema (3) tal que γβ ^-1 < Ŝ < a.

(c) Si ω₁ < f (a) < «0 entonces existen soluciones de equilibrio no trivial (Ĝ ₁ , Ŝ ₁ , 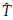₁ ), (Ĝ ₂ , Ŝ₂, 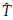₂) y (Ĝ₃, Ŝ₃, 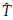₃) para el sistema (3) tal que γβ ^-1 < Ĝ ₁ < a, a < Ĝ₂ < a + ∈ ya + ∈< Ĝ₃ < 1.

Demostración. (a) Considere el intervalo γβ ¹ < G ≤ a.

Esto quiere decir que la función m no posee raíces para γβ ^-1 < G ≤ a. Por lo tanto no existe solución de equilibrio en dicho intervalo. Ahora, considere el intervalo a < G < a + ∈.

Por lo anterior la función m no posee raíces para a < G < a + ∈ y en consecuencia no existe solución de equilibrio en dicho intervalo. Por último considere el intervalo a + ∈ < G < 1, entonces m(1) = f(1) - ω₁ < 0,m(a + ∈) > 0 y m'(G) < 0. Lo cual significa que la función m posee raíces para a + ∈< G < 1yen consecuencia existe solución de equilibrio en dicho intervalo.

(b) Consideremos el intervalo γβ ^-1 < G < a, entonces tenemos que m(a) = f (a) - ω₀ = ω₁ - ω₀ < 0,m(γβ ^-1) = 00 y m'(G) < 0. Esto prueba que la función m posee raíces en el intervalo γβ ^-1 < G ≤ a y que por tanto existe solución de equilibrio en dicho intervalo. Ahora, considere el intervalo a ≤ G ≤ a + ∈, entonces

Lo anterior prueba que la función m no posee raíces en el intervalo a < G < a + ∈. En consecuencia no existe solución de equilibrio en dicho intervalo. Por último considere el intervalo a + ∈ ≤ G ≤ 1.

Por lo anterior la función m no posee raíces para a + ∈ < G < 1. En consecuencia no existe solución de equilibrio en dicho intervalo. En conclusión, existe una solución G tal que γβ ^-1 < G < a con las condiciones dadas.

(c) Considere el intervalo γβ ^-1 < G < a. Entonces, m(a) = f (a) - ω₀ < 0, m(γβ ^-1) = 00, m'(G) < 0. Lo anterior prueba que la función m posee raíces en el intervalo γβ ^-1 < G < a y en consecuencia existe solución de equilibrio en dicho intervalo. Ahora, considere el intervalo a ≤ G ≤ a + ∈.

Esto prueba que la función m posee raíces en el intervalo a < G < a+∈ y por lo tanto existe solución de equilibrio en dicho intervalo. Por último considere el intervalo a + ∈ ≤ G ≤ 1, para el cual tenemos que m(a + ∈) > 0,m'(G) < 0, y m(1) = f (1) - ω(1) < 0. Por tanto la función m posee raíces para a + e < G < 1. En consecuencia existe solución de equilibrio en dicho intervalo. En conclusión, existen tres soluciones de equilibrio G₁, G₂ y G₃ tal que γβ ^-1 < G₁ < a, a < G₂ < a + ∈ y a+∈<G ₃<1conlascondicionesdadas.

Ejemplo 8. Presentamos algunas simulaciones para el lema anterior

a) Considere los siguientes valores para los parámetros demográficos, μ = 0,3, Υ = 0,3, β = 0,7, ω₀ = 0,6, ω₁ = 0,4, a = 0,5, e = 0,05. Con estos valores se obtiene que f (1) = 0,225 < 0,4 = ω₁ y además, f (a) = 1,8 > 0,6 = ω₀. En consecuencia se cumple el primer caso del lema anterior, por tanto, existe una solución de equilibrio tal como lo muestra laFigura 14.

Figura 14: Existencia de soluciones de equilibrio para el caso (a) del Lema 5. 

b) Consideramos ahora los siguientes valores para los parámetros demográficos, j = 0,4, y = 0,2, β = 0,6, ω₀ = 0,75, ω₁ = 0,6, a = 0,6, e = 0,01. Se obtiene que f (1) = 0,2 < 0,6 = ω₁ y además, f (a) = 0,5 < 0,6 = ω₁ .En consecuencia se cumple el segundo caso del lema anterior, por tanto, existe una solución de equilibrio tal como lo muestra laFigura 15.

Figura 15: Existencia de soluciones de equilibrio para el caso (b) del Lema 5. 

c) Considere los siguientes valores para los parámetros demográficos, μ = 0,2, y = 0,1, β = 0,8, ω₀ = 0,2, ω₁ = 0,08, a = 0,4, e₁ = 0,01 y ∈₂ = 0,08. Con los parámetros mencionados previamente se cumple el caso (c) del lema anterior. Se tienen tres soluciones de equilibrio, sin embargo, dicha existencia depende del parámetro e. En laFigura 16se observa que para e = 0,01 se logran obtener las tres soluciones (caso A). Mientras que cuando se toma e = 0,08 solo se obtiene una solución (Caso B).

5.2. Análisis de estabilidad

En esta sección se determina una condición para que las soluciones halladas en la sección anterior sean asintóticamente estables. En primera instancia, miremos un resultado relacionado con la estabilidad de la solución de equilibrio trivial.

Figura 16: Existencia de soluciones de equilibrio para el caso (c) del Lema 5. 

Teorema 3. Si ω₁ (β - γ) < γμ entonces el equilibrio (1,0,0) del sistema (14) es asintóticamente estable.

Demostración. La matriz de linealización en la solución de equilibrio trivial es

Note que la traza de esta matriz es negativa. En consecuencia, se debe garantizar que det J(1,0,0) > 0 para concluir que la solución es asintóticamente estable (Teorema 5). Esto es, det μ(1,0,0) = μ (ω₁ + γ) + ω₁ (γ - μ - β) > 0, entonces debemos tener que μγ + ω₁ γ - ω₁ β > 0 ó μγ - ω₁ (β - γ) > 0. En conclusión, el equilibrio trivial es estable siempre que ω₁(β - γ) < μγ.

A continuación, presentamos un resultado que nos ayudará a determinar la estabilidad de las soluciones de equilibrio no triviales por medio de la función f, descrita en (16).

Proposición 4. Cualquier equilibrio no trivial (Ĝ, Ŝ, 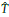) es asintóticamente estable siempre que

donde el lado izquierdo de la expresión es la derivada del parámetro « mientras que el lado derecho es la derivada de la función f, descrita en la ecuación (16).

Demostración. Determinemos la matriz de la comunidad del modelo (14),

Note que la traza de la matriz es negativa, por tanto, por las condiciones del Teorema 5 los equilibrios antes mencionados serán asintóticamente estables siempre que det J(Ĝ, 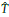, Ŝ) > 0. Denotemos como A al producto de la diagonal principal, mientras que B será el producto de la diagonal secundaria de la matriz j(g, t, S). Ahora se reducirá las expresiones para A y B teniendo en cuenta la Proposición 3 y el parámetro « evaluado en G. Se hará un abuso de la notación para reducir escritura, tomando ω = ω(Ĝ) y ω' = ω'(Ĝ). Empecemos por reducir A, esto es

Haciendo lo propio con B obtenemos

Por la condición que debe satisfacer el determinante tenemos que de

Por último, despejando ω' de la desigualdad anterior se obtiene la expresión deseada.

En la sección pasada probamos que pueden existir hasta cuatro soluciones de equilibrio, sin embargo, no se conoce nada acerca de su estabilidad. A continuación se presenta un resultado, cuya demostración es consecuencia directa de la Proposición 4, que da razón de la estabilidad de las soluciones de equilibrio no triviales.

Corolario 3. Dada una solución de equilibrio no trivial (Ĝ, Ŝ, 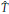) se cumple que

a) es asintóticamente estable si γβ ^-1 < G < a ó a + ∈ < Ĝ < 1.

b) es inestable si a < Ĝ < a + ∈.

Ejemplo 9. Considere los parámetros demográficos del literal c) del ejemplo 8 (Caso A). De acuerdo a lo expuesto enla sección pasada, en especial el Lema 5, existen cuatro soluciones de equilibrio que se describen a continuación

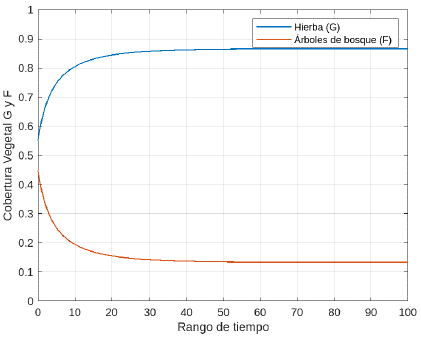
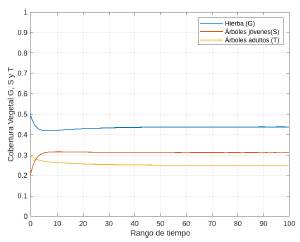
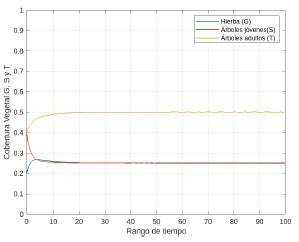
Con estos valores se obtienne que f (1) = 0,03 < 0,08 = ω₁ y además, f (a) = 0,09 < 0,20 = ω₀, f (a) = 0,09 > 0,08 = ω₁. Por el Corolario 3, se puede aseverar que las soluciones de equilibrio E ₁ y E ₃ son inestables, mientras que las otras serán asintóticamente estables. Para analizar la estabilidad del equilibrio E ₂ , se toma el valor inicial (G(0), S(0), T(0)) = (0,50,0,20,0,30). Como se observa en laFigura 17, el sistema evoluciona rápidamente a la solución E ₂ .

Por otra parte, si se toma el valor inicial (G(0), S(0), T(0)) = (0,40,0,40,0,20), el sistema evoluciona rápidamente al otro equilibrio estable, es decir E ₄ , tal como se observa en laFigura 18.

Figura 17: Dinámica del sistema para la condición inicial (G, S, T) = (0,50, 0,20, 0,30). 

Figura 18: Dinámica del sistema para la condición inicial (G, S, T) = (0,40, 0,40, 0,20). 

En términos ecológicos, la simulación hecha en este ejemplo permite evidenciar que coexisten dos equilibrios simultáneamente estables. Uno de ellos está asociado a la ausencia de fuego, en este caso se habla del equilibrio E ₂ . Bajo estas condiciones, predominan los árboles de sabana adultos. Por otra parte, cuando hay incidencia de incendios el sistema tiende a un estado en el que predomina la hierba (asociado al equilibrio E ₄ ), en cuyo caso, esta es la dinámica usual de los biomas de sabana.

Ejemplo 10. Considere los parámetros demográficos del ejemplo 7. De acuerdo a lo expuesto en la sección pasada, en especial el Lema 4, existen tres soluciones de equilibrio que son E1 = (1,0,0), E₂ = (0,427,0,109,0,464) y E ₃ = (0,448,0,115,0,437). Con estos valores de los parámetros se obtiene que f(1) = 0,2 > 0,15 = ω₁ y además, f(a) = 0,79 < 0,85 = ω₀. Por el Corolario 3, se tiene que E ₁ y E ₂ son asintóticamente estables, mientras que E ₃ es inestable. Si se toma el valor inicial (G(0), S(0), T(0)) = (0,60,0,30,0,10), el sistema evoluciona rápidamente al equilibrio E1, como se muestra en laFigura 19.

Ahora, estudiaremos la estabilidad del equilibrio E ₂ . Para ello, tomaremos el valor inicial (G(0), S(0), T(0)) = (0,40,0,10,0,50). En este caso, como se observa en laFigura 20, el sistema evoluciona rápidamente a este equilibrio.

Nuevamente, se obtienen dos equilibrios estables. Cuando hay incidencia de incendios, los árboles de sabana tienden a desaparecer, evolucionando a un estado donde la hierba es la única variable que se encuentra. Sin embargo, cuando hay ausencia de fuego, los árboles adultos de sabana predominan.

Figura 19: Dinámica del sistema para la condición inicial (G, S, T) = (0,60,0,30,0,10). 

Figura 20: Dinámica del sistema para la condición inicial (G, S, T) = (0,40,0,10,0,50). 

6. Coexistencia de Hierba (G) y árboles (S,T,F)

En esta última sección se presentan las múltiples soluciones de equilibrio del modelo propuesto por Staver y Levin en [¹⁵], teniendo en cuenta las modificaciones propuestas por Brhane en [²]. Así mismo, se realiza un análisis del tipo de estabilidad que posee cada equilibrio.

6.1. Soluciones de equilibrio

Inicialmente encontraremos las soluciones de equilibrio del sistema con presencia de todas las variables de estado, es decir, hierba (G), árboles de sabana jóvenes (S), árboles de sabana adultos(T) y árboles de bosque (F); mirando los equilibrios y la dinámica poblacional que puede ocurrir entre ellos. En este caso el sistema que se estudiará será el descrito en (2).

El equilibrio trivial del sistema se presenta cuando todo el espacio es ocupado por hierba, esto es, G = 1y S = T = F = 0. Por otra parte, si S > 0, T > 0, F > 0, usando la definición 2 las soluciones de equilibrio del sistema deben satisfacer el siguiente sistema de ecuaciones

Teniendo en cuenta que F > 0, de la última ecuación de este sistema se obtiene la condición a (1 - F) - ϕ(G) = 0, con lo cual se obtiene que

Note que la expresión anterior tiene validez siempre que α > ϕ(G). Ahora, determinemos una razón entre las variables S y T teniendo en cuenta la segunda ecuación del sistema (18)

Haciendo lo propio con la tercer ecuación de (18) tenemos

Así hemos probado el siguiente resultado

Proposición 5. Toda solución de equilibrio no trivial ( 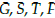) del sistema (2) debe satisfacer que,

donde ≠ 0.

Esto se puede combinar para encontrar una condición en términos de G,

De acuerdo a la condición presentada anteriormente, se pueden encontrar un máximo de cuatro soluciones de equilibrio (una de ellas es la trivial), tal como se observa en la Figura 21.

Figura 21: Análisis gráfico de los equilibrios internos. Adaptación de figura en [¹⁵]. 

6.2. Análisis de estabilidad

En este apartado se determinan condiciones para que las soluciones

de equilibrio del sistema (2) sean asintóticamente estables. En primer lugar, se hace una reducción del sistema por medio de la condición espacial, es decir, teniendo en cuenta que S(t) = 1 - G(t) - T(t) - F(t), en cuyo caso se obtiene el sistema

Teniendo en cuenta la forma de las soluciones de equilibrio, la matriz de la comunidad del modelo (19) es

Teorema 4. Sea ( 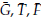) una solución de equilibrio no trivial del sistema (19).

a) Si ω( 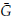) ≪ 0 y ϕ( 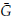) ≫ 0, entonces la solución de equilibrio es asintóticamente estable.

b) Si «( 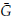) <3c 0 y 0( 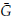) ≫ 0, entonces la solución de equilibrio es inestable.

Demostración. (a) Para este caso la matriz de la linealización será

Es evidente que la traza de la matriz jacobiana es negativa, resta verificar las otras dos condiciones.

■ Condición det J ( 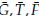) < 0: El determinante se puede obtener a través de det J = - 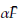. det M ₃₃ , donde M ₃₃ es la menor de la matriz J( 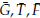) que se obtiene al eliminar la tercer fila y columna.

En consecuencia el determinante de J ( 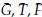) es negativo debido a que det M ₃₃ > 0.

Condición detJ(33, T,F) > tr J( 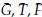). α₂ Por último, resta corroborar la tercera condición, realizando algunos cálculos y utilizando lo hallado previamente con respecto al determinante se obtiene que

En conclusión, una solución de equilibrio del sistema (2), tal que ω'(G) ≈ 0 y ϕ'(G) ≈ 0, será asintóticamente estable.

(b) La traza de j( ) bajo estas condiciones es positiva, debido a que ϕ' es suficientemente grande. Por tanto, una solución de equilibrio del sistema (2) es inestable.

El siguiente resultado es consecuencia inmediata del Teorema 4.

Corolario 4. a) Toda solución de equilibrio no trivial G tal que 0< G< aóa+∈< G< 1esasintóticamente estable.

b) Toda solución de equilibrio no trivial G tal que a < G < a + ∈ es inestable.

Ejemplo 11. Considere los siguientes valores para los parámetros demográficos, j = 0,03, γ = 0,26, β = 0,86, ω₀ = 0,63, ω₁ = 0,13, a = 0,687, ∈₁ = 0,0093, ϕ0 = 0,6 y ϕ₁ = 0,68. Para las condiciones dadas, se encuentran las siguientes soluciones de equilibrio

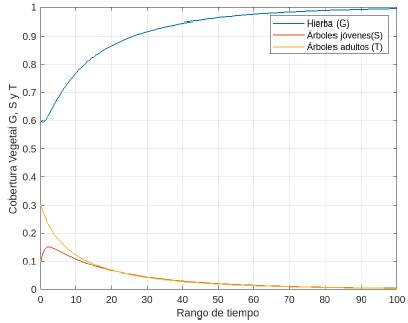
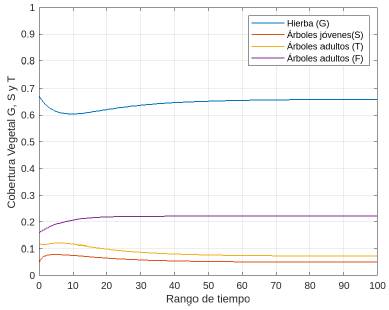
En este caso, por el corolario 4 se puede garantizar que E ₂ y E ₄ son asintóticamente estables, mientras que E3 será inestable. Para analizar la estabilidad del equilibrio E ₂ ,setomaelvalorinicia(G(0),S(0),T(0),F(0)) = (0,67,0,05,0,12,0,16). Como se observa en lafigura 22, el sistema evoluciona rápidamente a la solución E ₂.

Figura 22: Dinámica del sistema para la condición inicial (G,S,T,F) = (0,67,0,05,0,12,0,16). 

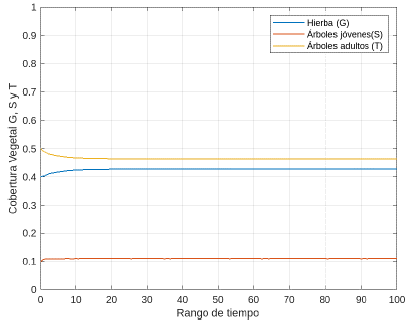
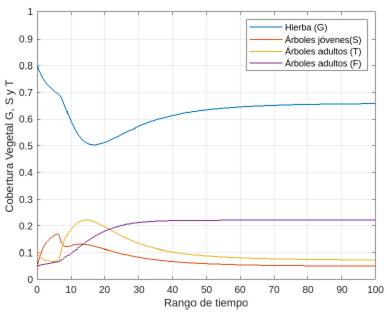
Por otra parte, si se toma el valor inicial (G(0),S(0),T(0),F(0)) = (0,80,0,05,0,10,0,05), el sistema evoluciona rápidamente al otro equilibrio estable, es decir E4, tal como se observa en laFigura 23.

En este tipo de trabajos es importante además de caracterizar las soluciones de equilibrio, reconocer las soluciones periódicas que pueden ocurrir bajo ciertas condiciones. Sin embargo, dicho análisis se sale de los objetivos del presente trabajo, aunque hay que aclarar que si existen soluciones periódicas para este modelo. Si se desea conocer más al respecto, el lector puede revisar [¹⁵].