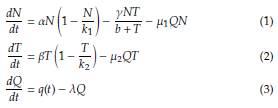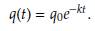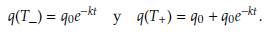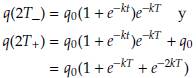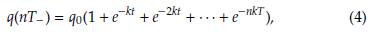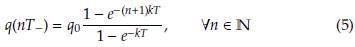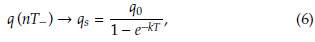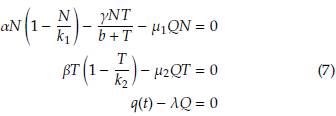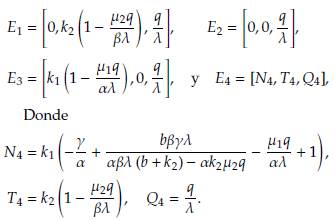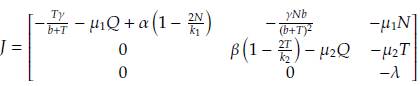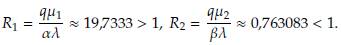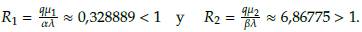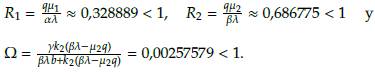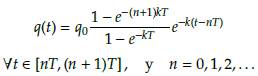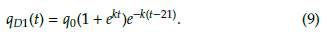1. Introducción

El cáncer es la segunda causa de muerte en la Región de las Américas. Se estima que 4 millones de personas fueron diagnosticadas en 2020 y 1,4 millones fallecieron a causa de esta enfermedad. Aproximadamente el 57 % de los nuevos casos de cáncer y el 47 % de las muertes ocurren en personas de 69 años o menos, [¹]. En Colombia, el cáncer tiene una incidencia estimada de 182 por 100.000 habitantes y la mortalidad es cercana a 84 por 100.000 habitantes. Aunque el cáncer se considera una enfermedad silenciosa y puede afectar a cualquier persona, alrededor del 30 % de las muertes por cáncer se deben a cinco factores de riesgo fundamentales como: alto índice de masa corporal, consumo insuficiente de frutas y verduras, falta de actividad física y consumo de tabaco y alcohol.

El cáncer es el resultado de un proceso de división celular irregular, donde las células cancerosas se caracterizan por no tener la dinámica de crecimiento de las células normales. Los procesos de división y muerte de estas células tumorales son irregulares en comparación con los de las células normales [²].

Durante la conversión maligna de células normales en células cancerosas, ocurren muchos cambios genéticos [³], en este proceso se produce una pérdida de control sobre los mecanismos de replicación y reparación de ADN, así como la desintegración del material genético. Aunque las células normales tienen estrategias de defensa contra el crecimiento del cáncer, las células cancerosas activan diferentes vías de escape que permiten el progreso del cáncer. Las células tumorales difieren de las células normales en muchos aspectos, que incluyen la pérdida de la capacidad de diferenciación, mayor invasividad y menor sensibilidad a los fármacos citotóxicos (sustancias con alta toxicidad). Estas características son el resultado de proliferación celular descontrolada y el desarrollo de células normales en células potencialmente cancerosas. Las células normales y tumorales compiten por espacio y requisitos como el oxígeno suministrado por los vasos sanguíneos [⁴].

Cuantas más células se vuelven anormales, más desarrollan capacidades para liberar factores de crecimiento y enzimas digestivas. A medida que las células anormales se dividen, afectan a las células normales vecinas, lo que a veces reduce la función del órgano afectado. Incluso las células cancerosas anormales mueren y un tumor lo suficientemente grande como para ser palpable puede tardar años en crecer hasta alcanzar un tamaño considerable. Aunque no todos los cánceres alcanzan las mismas etapas, existen algunas características comunes que muchos cánceres comparten en su proceso de desarrollo, entre estas características, destacamos la etapa en la que el crecimiento del tumor conduce al aumento del suministro de sangre, un proceso biológico llamado angiogénesis, en este proceso la sangre proporciona nutrientes, transporta productos de desecho y los vasos sanguíneos permiten que las células sanguíneas se muevan por todo el cuerpo [²].

Un tratamiento de cáncer ampliamente adoptado es la quimioterapia, que consiste en la administración de uno o más fármacos para actuar contra las células tumorales. Según [⁶], los tumores malignos se caracterizan por la formación de células alteradas, provocando cambios en los mecanismos de regulación de su división. Cuando esto ocurre, esas células pueden multiplicarse, invadir y afectar sin control órganos cercanos o distantes en un proceso llamado metástasis. Cada vez que se forma una nueva célula, se espera que se someta a un proceso biológico para convertirse en una célula completamente funcional (o madura), este proceso implica una serie de etapas del ciclo celular. Durante la división celular existe la mayor probabilidad de que ocurran cambios anormales en la célula y es por esto que el tratamiento de quimioterapia actúa sobre las células en diferentes etapas del ciclo celular. Según el efecto biológico de los medicamentos los especialistas pueden predecir qué combinaciones de medicamentos tienen más probabilidades de funcionar, así como la frecuencia de dosificación, que, a su vez, se basa en la duración de la fase celular [⁵].

El tratamiento quimioterápico puede administrarse de forma esporádica o no. En algunos casos, la administración de los fármacos en un corto período de tiempo erradica el tumor. Sin embargo, en la mayoría de los casos, incluso una dosis más alta no puede erradicar las células tumorales, lo que justifica una exposición prolongada al tratamiento repitiendo las dosis del fármaco. Esos protocolos clínicos permiten que más células tumorales sean consideradas en el ciclo y consecuentemente erradicadas [⁷].

Las células cancerosas tienden a formar nuevas células más rápido, lo que facilita que los medicamentos de quimioterapia actúen sobre su control. Dado que la terapia con medicamentos no puede distinguir entre células sanas y células cancerosas, las células normales se ven afectadas junto con las células tumorales durante todo el tratamiento, lo que provoca efectos secundarios. Cada vez que se administra una sesión de quimioterapia, se intenta equilibrar la destrucción de las células cancerosas (curar o controlar la enfermedad) y proteger las células normales para reducir los efectos secundarios. A pesar de los efectos secundarios sobre las células no tumorales del tratamiento de quimioterapia, la mayoría de las células normales tienen la capacidad de recuperarse de los efectos de la quimioterapia, lo que no ocurre con las células cancerosas en general.

Existen dos tipos de tratamiento de quimioterapia dependiendo del ciclo celular del tumor. El tratamiento ciclo-específico que permite la supresión de las células existentes en un ciclo celular específico durante un tiempo corto, siendo necesario aumentar la dosis para actuar contra el tumor de forma eficaz. Y el tratamiento no específico del ciclo que se realiza en cualquier fase del ciclo celular, se utiliza habitualmente en el tratamiento de tumores de gran tamaño, ya que en estos casos la actividad de división celular es menor. En este último tratamiento, el número de células destruidas es directamente proporcional a la dosis administrada [⁷]. El tratamiento de quimioterapia no específica de ciclo se considerará para el modelado y posterior análisis en este documento.

Las principales causas de fallas en el procedimiento pueden ser: 1^o Un diagnóstico tardío que generalmente implica un tumor de volumen considerable resistente al tratamiento; 2^o Número insuficiente de dosis; 3^o Un segundo tumor emergente resistente a los medicamentos; 4^o Una resistencia al tratamiento debido al conteo de dosis bajas; o 5^o Un gran intervalo de tiempo entre dos dosis sucesivas, lo que puede causar resistencia al tratamiento.

Otros tratamientos anticancerígenos con intervalos de tiempo más cortos, llamada quimioterapia con metrónomo, por ejemplo, que tiene un intervalo de tiempo entre dosis de 6 días y ha demostrado ser una opción útil en el tratamiento del carcinoma de pulmón [⁸]. Este tratamiento tiene como objetivo eliminar las células endoteliales responsables de la vascularización del tumor.

Este artículo presenta un modelo químico de dos células para la dinámica de crecimiento tumoral bajo tratamiento de quimioterapia. En el modelo, llamamos células normales a las células no tumorales, es decir, aquellas que presentan la dinámica de crecimiento esperada para las células sanas, vale la pena señalar que esta población celular incluye las células inmunitarias, aunque no se diferencian del resto de células del torrente sanguíneo. Esto significa que el modelo no considera la acción de las células efectoras en la descomposición tumoral. Este trabajo pretende proponer protocolos efectivos de tratamiento quimioterapéutico para combatir las células tumorales, además de ayudar a establecer si la quimioterapia debe preceder a la cirugía o viceversa. Abordamos esas preguntas desde un punto de vista analítico y numérico, lo que nos lleva a una comprensión innovadora de la dinámica del crecimiento tumoral.

El resto de este documento está organizado de la siguiente manera: La sección Discusión presenta un modelo matemático para la dinámica de crecimiento tumoral considerando el efecto de la quimioterapia sobre dos poblaciones de células, se presenta una descripción, y un estúdio matemático de puntos estacionarios y su correspondiente análisis de estabilidad de los puntos estacionarios del modelo. La sección Resultados presenta algunas simulaciones numéricas realizadas en cuatro diferentes escenarios y finalmente en Conclusiones se presentan algunas consideraciones finales sobre los resultados proporcionados en este trabajo.

2. Discusión

Esta sección presenta un modelo de un fármaco sobre dos poblaciones celulares, considerando tres compartimentos: población de células tumorales, población de células normales y tratamiento de quimioterapia. Las funciones N(t), T(t) y Q(t) respectivamente representan el recuento de células normales, células tumorales y la concentración de fármaco en el torrente sanguíneo en el instante t > 0. Consideramos que tanto las células normales como las tumorales crecen logísticamente. Además, la población de células normales se ve afectada por las células tumorales mediante una dinámica llamada de Michelis-Menten, que refleja el crecimiento tumoral limitado por saturación, para más detalles se recomienda estudiar la referencia [⁹]. El efecto del fármaco sobre las células tumorales y los efectos secundarios de la quimioterapia sobre las células normales están dados por dinámicas de ley de acción de masas. También suponemos que la quimioterapia se administra en sesiones periódicas, lo que se espera que provoque un aumento de la concentración del fármaco en el torrente sanguíneo. Finalmente asumimos que la descomposición del fármaco es exponencial.

Sea q: [0, ∞) → ℝ la función que representa la administración periódica del fármaco, la dinámica de crecimiento tumoral bajo tratamiento de quimioterapia y sus interacciones con células no tumorales (o células normales) se representa mediante el siguiente sistema de ecuaciones diferenciales no lineales:

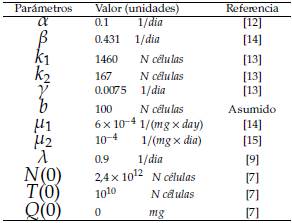
La figura 1 ilustra la dinámica entre las dos poblaciones celulares N(t) y T(t) bajo el efecto del tratamiento quimioterapeutico, los parámetros utilizados en las ecuaciones son descritos en la tabla 1.

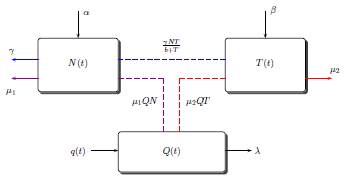
Figura 1: Representación de la dinámica entre el tumor y las células normales bajo el tratamiento de quimioterapia periódica dada por q(t). 

2.1. Descripción del modelo

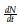: Tasa de cambio de celulas normales

La población de células normales crece en función de un crecimiento logístico con tasa de crecimiento intrínseco a y capacidad de soporte k ₁ , disminuye en interacción con células tumorales donde es utilizada una función de Michelis-Menten para modelar dicho comportamiento, en este caso y representa la tasa en la cual las células normales disminuyen en interacción con las células tumorales y b representa el número de células en la cual la disminución es igual a la mitad de su máximo, para más detalles revisar [¹⁰].

El último término representa la afectación de células normales a causa del tratamiento quimioterapeutico con tasa μ ₁.

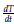: Tasa de cambio de las células tumorales

Análogamente las células tumorales experimentan un crecimiento logístico con tasa de crecimiento intrínseco β y capacidad de soporte dada por k₂. De igual forma el último término representa la afectación del tratamiento quimioterapeutico a las células tumorales con tasa μ ₂.

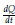: Tasa de cambio de la concentración del fármaco

La ecuación (3) depende de una función por partes q = q(t) relacionada con la administración periódica del fármaco, que aumenta la concentración del fármaco. Además, consideramos el decaimiento exponencial en el torrente sanguíneo con A constante, como se explica en [¹¹].

Destacamos el papel de la función q, que representa la administración periódica de medicamentos. Suponemos que q está relacionado con la cantidad de medicación administrada en cada sesión de quimioterapia, por lo que consiste en una función definida por tramos. Suponemos también que el intervalo de tiempo entre dos sesiones está dado por T > 0, el cual debe ser determinado por los protocolos médicos de cada individuo.

Si suponemos que q(0) = q0 la cantidad de fármaco absorbido por un individuo en la primera sesión de quimioterapia, que se administra en el instante t = 0. Si la descomposición del fármaco es exponencial con una tasa constante k, entonces la concentración del fármaco en el torrente sanguíneo en el primer intervalo de tiempo [0, T] viene dada por

La segunda sesión de quimioterapia se administra en el momento T. Por lo tanto, la concentración del fármaco antes y después de la segunda dosis del medicamento puede representarse por q(T_) y q(T ₊ ), respectivamente, donde

En consecuencia, la concentración del fármaco en el torrente sanguíneo en el intervalo [T, 2T], correspondiente al lapso de tiempo entre la segunda y la tercera sesión de quimioterapia, está dada por q(t) = q₀(1 + e^-kt)e^-k(t-T), para todo t en [T, 2T].

Suponiendo que el tratamiento sigue un intervalo de tiempo dado por T días, la tercera sesión de quimioterapia se administra en el momento t = 2T, de donde la concentración del fármaco antes y después de la tercera dosis se puede representar por q(2T_) y q(2T ₊ ) respectivamente, donde

Por lo tanto, la concentración de fármaco en el torrente sanguíneo en el intervalo [2T, 3T], correspondiente al lapso de tiempo entre la segunda y la tercera sesión, está dada por q(t) = q ₀(1 + e ^-kt + e ^-2kt )e ^-k(t-2T) , para todo t en[2T,3T].

Tabla 1: Descripción de los parámetros 

Podemos extender el razonamiento anterior a una sucesión de sesiones de quimioterapia administradas en cada intervalo de tiempo dado por T días. Inmediatamente después de N administraciones de medicamentos, la concentración de drogas en el torrente sanguíneo

Como1+e - ^kT +e ^2kT +···+e - ^nkT representa una progresión geométrica con razón e - ^kT , podemos reescribir la ecuación (4) como:

Así, cuando n aumenta, tenemos que

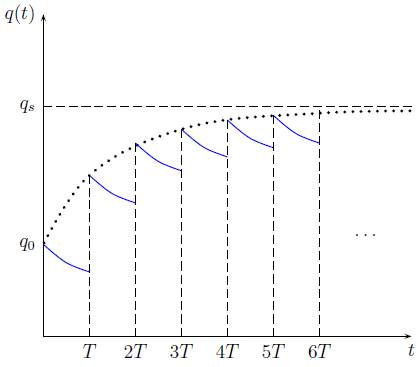
Que representa la saturación máxima de la droga en el torrente sanguíneo. El valor q _s puede verse como un umbral de la concentración del fármaco, que no se supera al final del tratamiento a pesar de la cantidad de sesiones de quimioterapia suministradas, como se muestra en la figura 2.

Figura 2: Descripción de la función q y el umbral q _s , dado por la ecuación (6). La función q representada en color azul continua y el umbral q _s es representado por la línea discontinua superior. 

2.2. Puntos Estacionarios

Los puntos estacionarios del modelo son las soluciones del sistema homogéneo asociado al sistema, esto es:

Considerando q(t) = q > 0 constante, estas soluciones son:

El punto estacionario E1 representa el caso en el que las células normales se extinguen y tanto las células tumorales como la concentración del fármaco alcanzan valores de equilibrio. Biológicamente, este escenario se interpreta como la falla de la función del tejido u órgano afectado por el cáncer, lo que implica la muerte del individuo.

El estado estacionario E ₂ es una solución del sistema homogéneo que carece de interpretación biológica, puesto que implica que las dos poblaciones celulares se extingan al transcurrir el tiempo.

El punto estacionario E₃ representa el escenario donde las células tumorales están extintas, y tanto las células normales como las concentración de fármaco alcanzan los valores de equilibrio. Biológicamente este caso describe la recuperación del individuo y la regresión total del cáncer. Uno puede esperar que este caso ocurra después de un tiempo de tratamiento, ya que la eliminación del tumor no ocurre en ausencia de este.

Por último, el punto estacionario E4 representa el caso donde las células normales y tumorales, así como la concentración de fármaco, alcanzan los valores de equilibrio. En este escenario, ambas poblaciones de células coexisten en el tejido u órgano afectado.

Nótese que el valor de equilibrio para la concentración del fármaco es el mismo en los cuatro puntos estacionarios considerados en esta sección.

2.3. Análisis De Estabilidad

En esta sección proporcionaremos un análisis de estabilidad de los puntos estacionarios enumerados en la sección anterior. Considere la matriz jacobiana asociada al sistema dado por las ecuaciones (1) a (3), esta es:

Recuerde que la estabilidad local de los puntos estacionarios E ₁ , E ₂ , E ₃ , E ₄ está determinada por los valores propios de la matriz J evaluada en cada uno de estos puntos, esto es J(E _i ) ∀_i = 1,2,3,4. En particular, describiremos las regiones donde la parte real de los valores propios es negativa. Por lo tanto, tenemos cuatro casos que considerar:

1. Evaluando el primer punto estacionario E ₁ en la matriz J, tenemos que los valores propios de la matriz son: λ₁ = -λ, λ₂= 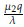-β y λ₃ = α-

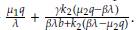
De esta manera, el punto estacionario E ₁ es localmente estable cuando βλ > μ ₂q y aλ < μ ₁q, ya que en estas condiciones la parte real de los valores propios λ₁, λ₂, λ₃ es negativa.

2. La matriz J evaluada en E ₂ tiene valores propios dados por λ₁ = -λ, λ₂ = α - 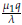y λ₃ = β - 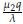. Así, el punto estacionario E ₂ es localmente estable cuando > 1 y 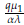> 1. Sin embargo, como se mencionó anteriormente, este punto no tiene una interpretación biológica válida, ya que implicaría la extinción de la población de células tanto normales como tumorales.

3. La matriz J evaluada en E ₃ tiene valores propios dados por: λ ₁ = - λ, λ ₂ = 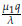- α, y λ₃ = β - 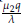. Así, el punto estacionario E ₃ es localmente estable cuando βλ < μ ₂ q y αλ > 1q. Tenga en cuenta que la estabilidad local de E ₃ contradice la estabilidad local de E ₁ , es decir, si E ₁ es localmente estable, entonces E3 es localmente inestable y viceversa.

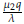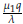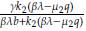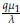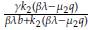4. La matriz J evaluada en E4 tiene valores propios dados por: λ1 = -λ, λ₂ = - β, y λ₃ = -α + + . Así, el punto estacionario E4 es localmente estable cuando qμ ₂ < βλ y α - > Ω= >0.

Cabe señalar que la estabilidad local de E3 implica la inestabilidad local de E ₄ . Además, la estabilidad de los cuatro puntos estacionarios está completamente determinada por los valores R₁ = 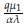y R₂ = 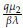cuando ellos son mayores o menores que 1. La figura 3 es la representación gráfica de las regiones de estabilidad para los puntos E _i .

3. Resultados

Simulaciones Numéricas

En esta sección se realizan simulaciones numéricas del sistema (1) a (3) asumiendo los parámetros denotados en la tabla 2 y utilizando el método numérico Runge Kuta de cuarto orden. Se muestran escenarios correspondientes a cada uno de los puntos estacionarios justificando numéricamente la estabilidad local estudiada anteriormente.

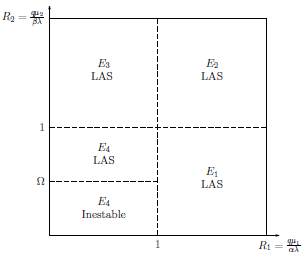
Figura 3: Diagrama de estabilidad de los puntos estacionarios E _i cuando i = 1, 2, 3, 4. En función de los valores de R ₁ y R ₂ , las líneas negras discontinuas separan las regiones de estabilidad local (LAS) de cada punto E _i . 

Tabla 2: Parámetros y condiciones iniciales utilizados en las simulaciones numéricas. 

A1. Extinción de Células Normales.

En este escenario con un periodo de T = 21 días la población de células normales se extingue, como se muestra en la figura 4, mientras que las células tumorales y el tratamiento quimioterapeutico permanecen constantes. Los parámetros y condiciones iniciales utilizados en esta simulación son los mostrados en la tabla 2, obteniéndose:

De esta manera, según la figura 3, se justifica numéricamente que el punto estacionario E1 = 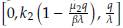es localmente estable (LAS).

A2. Extinción de Células Normales y Tumorales

En este escenario en un periodo de 21 días la población de células normales y tumorales se extingue, como se muestra en la figura 5, mientras que el tratamiento quimioterapeutico se estabiliza. Para este caso fueron modificados los parámetros μ ₁ = 0,0008 y μ ₂ = 0,0009 según las referencias de [¹³] y [¹⁴] y los parámetros restantes y condiciones iniciales se mantuvieron como se muestra en la tabla

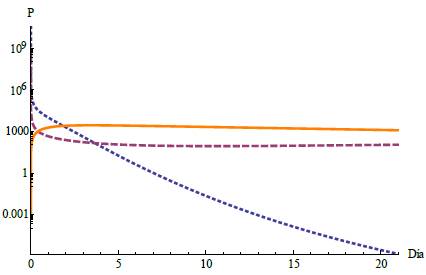
Figura 4: Caso 1. Extinción de células normales. La línea continua de color naranja representa la quimioterápia, la línea discontinua de color violeta representa a las células tumorales y la línea punteada de color azul representa a las células normales. Esta misma descripción se utilizará en las figuras siguientes. 

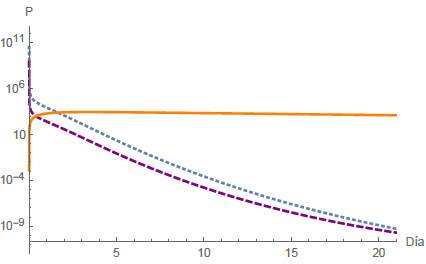
Figura 5: Caso 2. Extinción de células tanto normales como tumorales. La descripción de las curvas es similar a la que se explica en la figura 4  

2, con estos valores se obtuvo: R₁ = 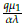≈ 26,3111 > 1 y R₂ = 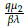≈ 6,86775 > 1.

Según la figura 3, los valores R ₁ y R ₂ anteriores justifican numéricamente la estabilidad local (LAS) del punto estacionario E ₂ = (N ₂, T ₂,Q ₂) = (0, 0, )

A3. Extinción de Células Tumorales.

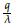Figura 6: Caso 3. Extincion de celulas tumorales. 

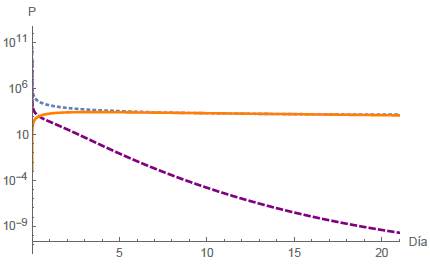
En este escenario en un periodo de T = 21 días la población de células tumorales se extingue, como se muestra en la figura 6, mientras que la población de células normales y el tratamiento quimioterapeutico se estabilizan. Para este caso se modificó los parámetros μ ₁ = 0,00001 (valor asumido por los autores) y μ ₂ = 0,0009 según la referencia [14]. Los parámetros restantes y condiciones iniciales son los mostrados en la tabla 2, obteniéndose:

De acuerdo con la figura 3, los valores de R1 y R₂ anteriores justifican numéricamente la estabilidad local (LAS) del punto estacionario E₃ = [k1(1 - 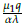) ,0, ].

Figura 7: Caso 4. Equilibrio celular. 

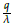A4. Equilibrio Celular

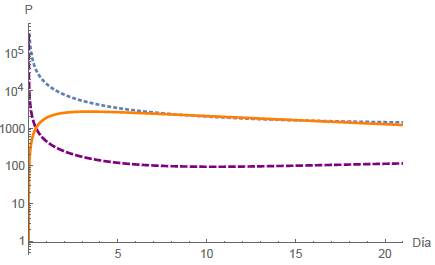
En este escenario en un periodo de T = 21 días la población de células normales y tumorales se estabilizan, como se muestra en la figura 7, mientras el tratamiento quimioterapeutico permanece constante. Para este caso se utilizaron μ ₁ = 0,00001 y μ ₂ = 0,00009 que fueron valores asumidos por los autores y los demás parámetros y condiciones iniciales son los mostrados en la tabla 2, con estos valores se obtuvo:

Note que R₂ > Q para obtener la estabilidad local deseada, pues si R₂ es menor a Q según el análisis de estabilidad realizado anteriormente, no se alcanza la estabilidad local. De esta manera, según la figura 3, se justifica numéricamente que el punto estacionario E ₄ = (N ₄, T ₄, O ₄) donde N ₄ = k ₁ 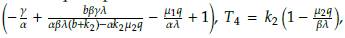y Q ₄ = 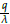, es localmente estable (LAS).

3.2. Caso B. Cuando q es Variable

En esta sección se estudia el caso en el que la función

Además, consideraremos diferentes valores para el intervalo de tiempo entre dos sesiones de quimioterapia, denotado por T, y una tasa de eliminación del fármaco dada por k = 0,05 (dia) ^-1 .

B1. Extinción de Células Normales.

Para la simulación numérica en este escenario consideramos 2 dosis posteriores a la dosis inicial q₀ = 2960, distribuidas en intervalos de tiempo de 21 días. De esta manera, a partir del tiempo inicial t ₀ = 0 y hasta el tiempo t = 21, la concentración del fármaco en la sangre es modelada por la función

De manera similar, desde el instante de tiempo t = 21 hasta el instante t = 42, el conteo de drogas en el torrente sanguíneo está modelado por la función

Los parámetros y condiciones iniciales son mostrados en la tabla 2 y el comportamiento se muestra en la figura 8.

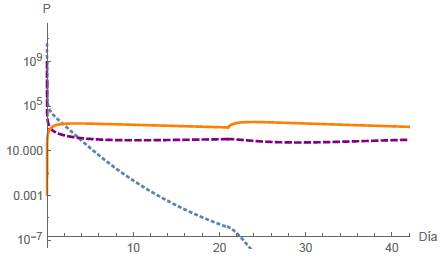
Figura 8: Caso B1, Extinción de céluas normales considerando dos periodos de 21 días. Los puntos finales están dados por N(42) = 2,4154 x 10^-19 células, T(42) = 96,8504 células y Q(42) = 1372,51 mg. 

Observamos que después del período de T = 21 días, las células normales, las células tumorales y el recuento de drogas están dados, respectivamente, por N(21) = 1,47x10^-6, T(21) = 106,45, Q(21) = 1182,15.

Por tanto, después de la primera sesión de quimioterapia, se erradica la población de células normales, lo que implica la pérdida de la función del tejido u órgano afectado. Por este motivo, se supone que el tratamiento se suspende después de la segunda sesión de quimioterapia.

Caso B4. Equilibrio celular

Análogamente al caso A4, cuando R1 < 1 y Ω < R₂ < 1 se tiene un escenario de equilibrio celular, y se espera la estabilidad local del punto estacionario E ₄ . Se presentan las simulaciones numéricas correspondientes a diferentes períodos de dosis, a saber, T = 21,14,7 días, representadas en las figuras 11, 12 y 13, respectivamente. En todos los casos asumimos la administración de seis dosis para el tratamiento. Cabe señalar que ninguna población es erradicada para diferentes valores del intervalo de tiempo T.

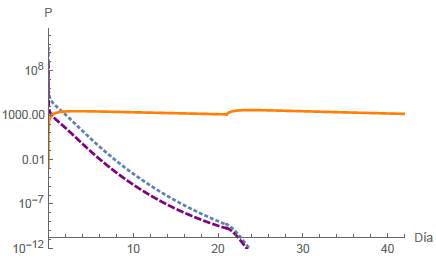
Figura 9: Caso B2, donde q es una función definida por partes y T = 21 días. Los puntos finales están dadas por N(42) = 2,4122x10^-27 células, T(42) = 5,0756 x 10^-27 células y Q(42) = 1372,51mg. 

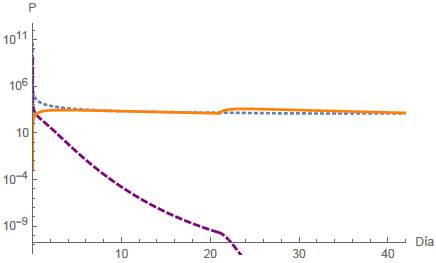
Figura 10: Caso B3, donde q es una función definida por partes y T = 21 días. Los puntos finales están dadas por N(42) = 1204,2 células, T(42) = 1,2301 x 10^-22 células y Q(42) = 2174,99mg. 

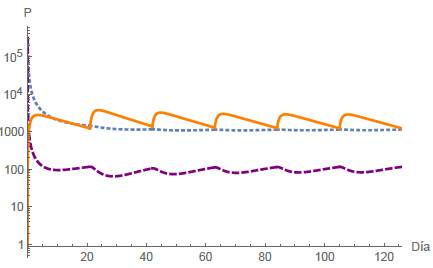
Figura 11: Caso B4, T = 21 días y n = 6. Los puntos finales están dadas por N(126) = 1138,93 células, T(126) = 115,494 células y Q(126) = 1216,86mg. 

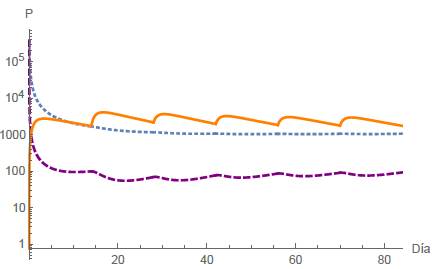
Figura 12: Caso B4, T = 14 días y n = 6. los puntos finales están dadas por N(84) = 1068,38 células, T(84) = 92,5029 células y Q(84) = 1751,34mg. 

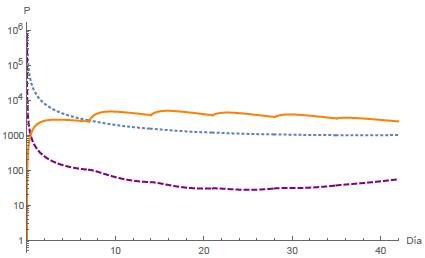
Figura 13: Caso B4, T = 14 días y n = 6. los puntos finales están dadas por N(42) = 1003,28 células, T(42) = 54,7899 células y Q(42) = 2456,44mg. 

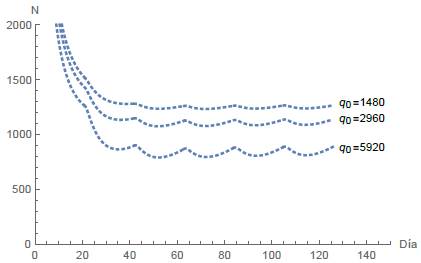
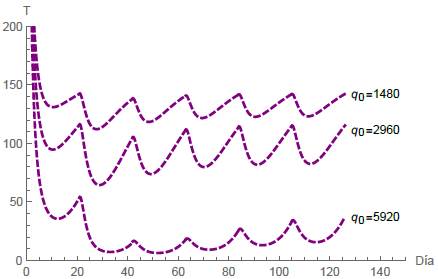
Al comparar diferentes valores para la dosis inicial del fármaco, observamos un efecto considerable sobre la población de células tumorales. Las siguientes simulaciones comparan tres dosis iniciales diferentes de quimioterapia y su efecto en ambas poblaciones celulares. Las figuras 14 y 15 muestran el comportamiento de las células normales y tumorales respectivamente, cuando la dosis inicial del fármaco q ₀ asume los valores de 1480mg, 2960mg y 5920mg.

Figura 14: Población de células normales con diferentes dosis iniciales de fármaco. 

Figura 15: Población de células tumorales con diferentes dosis iniciales de fármaco. 

4. Conclusiones

Este trabajo presenta un modelo de la acción de un fármaco sobre dos poblaciones celulares bajo tratamiento de quimioterapia. El modelo propuesto considera células normales y tumorales y la concentración del fármaco en el torrente sanguíneo a lo largo del tiempo. Se realizó una investigación sobre los puntos estacionarios del modelo y se presentó un diagrama detallado de las regiones de estabilidad local (LAS) de los puntos. El análisis de estabilidad del modelo produjo cuatro escenarios diferentes, a saber: 1⁰. Extinción de la población de células normales, 2⁰. Extinción de las poblaciones de células normales y tumorales, 3⁰. Extinción de las células tumorales, y 4⁰. Equilibrio de las poblaciones celulares. La administración de medicamentos fue representada por una función q: [0, ∞ ) → ℝ como una función constante y como una función variable definida por partes, que considera la administración de la quimioterapia en sesiones periódicas.

Las simulaciones numéricas permiten realizar interpretaciones biológicas en relación con los cuatro escenarios estudiados mencionados anteriormente. Considerando el caso de que q es constante. El primer escenario describe la extinción de la población de células normales como consecuencia de los efectos secundarios del tratamiento de quimioterapia, mientras que tanto la población de células tumorales como la densidad del fármaco alcanzan su estabilidad como se muestra en la figura 4, en este escenario el tejido u órgano afectado pierde sus funciones, lo que a largo plazo implicaría el fallecimiento del paciente. El segundo escenario describe la extinción de la población de células tanto normales como tumorales como consecuencia de los efectos del tratamiento quimioterapéutico, en el que la densidad del fármaco en el torrente sanguíneo alcanza su equilibrio, como se muestra en la figura 5). El tercer escenario describe la extinción de la población de células tumorales como consecuencia de los efectos terapéuticos del tratamiento de quimioterapia, mientras que tanto la población de células normales como la densidad del fármaco alcanzan su estabilidad, ver figura 6. En este caso, se espera la recuperación del individuo en un corto período de tiempo, esto puede considerarse como resultado de un diagnóstico temprano de cáncer o una buena adhesión al tratamiento. Por último, el cuarto escenario describe un equilibrio celular, en el que las poblaciones celulares se mantienen estables al igual que la densidad del fármaco en el torrente sangíneo, se debe resaltar que aunque la población de células tumorales se ve afectada por la quimioterapia, esto tratamiento no logra erradicar el tumor del tejido, ver figura 7. Cabe señalar que en todos los casos las simulaciones numéricas realizadas al modelo representan una dinámica local de un fármaco actuando sobre dos poblaciones celulares, donde fue posible realizar un análisis matemático de aspectos claves. Sin embargo, es posible que se pueda construir un modelo con mayores hipótesis en el que se pueda representar una dinámica global sobre el tejido u órgano afectado por el cáncer, pero en este caso el análisis matemático se vuelve más extenso y en ocasiones difícil de realizar.

Cuando el fármaco se administra en ciclos, se analizan los mismos cuatro casos mencionados anteriormente para diferentes intervalos de tiempo T. En el primer caso, en un período de T = 21 días junto con dos dosis administradas implica que la población de células normales se extinga, mientras que las células tumorales se estabilizan en un lapso de 42 días, como se representa en la figura 8. Análogamente en el segundo caso, donde T = 21 días y se administran dos dosis, tanto las células normales como las tumorales se extinguen rápidamente, ver figura 9. En el tercer caso, con ciclos de T = 21 días junto con dos dosis administradas, las células tumorales se extinguen, mientras que las células normales se estabilizan, ver figura 10. El cuarto caso se representa en las figuras 11, 12 y 13 para tres intervalos de tiempo diferentes para las sesiones de quimioterapia, a saber: T = 21,17,7 junto con seis sesiones en todos los casos. En este escenario observamos que las poblaciones de células alcanzan un equilibrio estable y además, cuanto menor es el intervalo de tiempo T, menor es la población de células tumorales. Además, se simularon diferentes valores para la dosis inicial de fármaco, lo que nos llevó a concluir que la eficacia del tratamiento de quimioterapia depende en gran medida de la cantidad de fármaco y del tiempo entre cada periodo, ver figuras 14 y 15.

Por último, el modelo propuesto en este trabajo sugiere que la combinación de la dosis inicial del fármaco junto con un intervalo de tiempo entre las sesiones de quimioterapia influye en la reacción tanto de las células normales como de las tumorales y, en consecuencia, en la eficacia del procedimiento quimioterapéutido. De esta manera, el uso de modelos matemáticos ha demostrado ser una herramienta innovadora en el estudio de la dinámica de crecimiento tumoral.