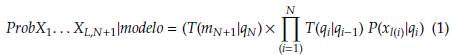2. Alineamiento local de secuencias de proteínas: BLAST

Las secuencias de proteínas homólogas son aquellas que comparten en términos evolutivos un ancestro común y pueden ser definidas matemáticamente desde la medida de similaridad en sus secuencias. BLAST [⁹] es un algoritmo diseñado para identificar coincidencias iniciales entre secuencias biológicas en una base de datos. BLAST fue lanzada en 1990, y desde ese momento el artículo que la describía se convirtió en uno de los más citados de la ciencia [¹⁰]. La razón: BLAST es un software Front End (disponible también con entornos gráficos) y disponible on-line, aspectos que resultan atractivos para muchos usuarios, se ha demostrado como una herramienta de investigación certera para el encuentro de secuencias homólogas con identidades mayores al 25 %, optimizada para acelerar el tiempo de respuesta de búsquedas de secuencias.

BLAST es una heurística [⁹], y como tal, es capaz de encontrar la mayoría de las coincidencias buscadas, aunque puede pasar por alto algunas (falsos negativos) o informar otras (falsos positivos), es capaz de encontrar coincidencias iniciales que luego se amplían con un algoritmo determinista, que como tal, puede encontrar exactamente el conjunto de aciertos en la consulta que de forma aproximada coincide dentro de un umbral especificado al unir métodos heurísticos con modelos deterministas BLAST permite que sus usuarios cuenten con un rendimiento en tiempos de ejecución superior. Para simplificar la búsqueda, BLAST, antes de comenzar, se realiza la partición de la secuencia consulta en palabras superpuestas de longitud k (k-mers) y genera un índice k-mer. Para iniciar la búsqueda de cada palabra en el vecindario en una tabla hash para encontrar la ubicación en la base de datos donde aparece cada palabra para la construcción de la colección de semillas, S. Las semillas desde la colección S se extienden hasta que la puntuación de la alineación descienda por debajo de algún umbral X. para finalmente reportar las coincidencias con las puntuaciones más altas.

Pese a todas las ventajas expuestas, BLAST es una herramienta poco eficiente para la identificación de secuencias con bajos porcentajes de identidad con sus homólogos. El software BLAST es desarrollado implementando el algoritmo de Smith-Waterman [⁸] el cual basa su uso en algoritmos de programación dinámica [¹¹] para alineamientos locales que determinan los aciertos con respecto a un sistema de puntajes llamado "Matrices de sustitución" que cuantifican la relación de una secuencia con otra.

Figura 1: Matriz de sustitución BLOSON62. Fuente: [¹²] 

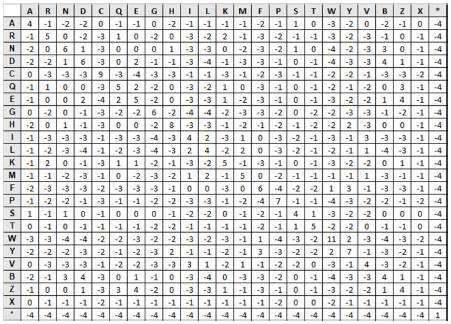
Una matriz de sustitución de aminoácidos figura 1 es la matriz BLOSUM 62 [¹²]. En términos generales las matrices BLOSUM se obtienen utilizando bloques de secuencias de aminoácidos similares como datos para a través de la aplicación métodos estadísticos a los datos obtener las puntuaciones de similitud como los valores proporcionales a la tasa a la que un aminoácido i cambia a un aminoácido j para todos los pares de aminoácidos posibles.

El tipo de matriz usada es determinante para los resultados que se obtendrán ya que cumple la función de asignar una puntuación a cada residuo emparejado. En principio, el uso de una matriz incorrecta puede llevar a calificar erróneamente los alineamientos y por lo tanto obtener resultados equivocados. No obstante, [¹³] reportó que la matriz BLOSUM 62 usada por defecto para los cálculos de BLAST contenía errores en el código fuente del software utilizado para crearla, además de diferencias a la descripción exacta del algoritmo descrito por [¹⁴] para las matrices BLOSUM. Este caso es digno de mención por tres razones: Primero, estas matrices BLOSUM se usan en infinidad de herramientas en biología computacional; segundo, estos errores pasaron desapercibidos durante 15 años; y tercero, las matrices "erróneas" funcionan mejor que las matrices que se obtienen usando exactamente el algoritmo descrito por Henikoff y Henikoff.

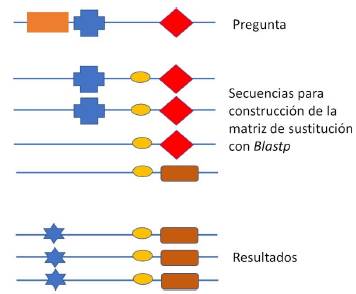
Aun así, es ineludible; tener en cuenta que, BLAST no dispone de matrices de sustitución específicas para cada una de las secuencias y organismos existentes, siendo esta la primera limitante, ya que las posiciones y los residuos específicos no necesariamente tienen los mismos patrones de conservación en diferentes contextos. El hecho de no poder contar con matrices específicas para el análisis de cada conjunto de proteínas ha hecho que soluciones computacionales alternativas sean propuestas en busca de algoritmos inteligentes capaces de aprender a fin de evitar la dependencia de parámetros fijos y generales como las matrices de sustitución. NCBI; por ejemplo, propone el software PSI-BLAST como alternativa [¹⁵], es un software capaz de crear nuevas matrices de sustitución a partir de alineamientos múltiples de secuencias obtenidos por búsquedas locales con BLASTp, facilitando el encuentro de secuencias con porcentajes de identidad inferiores al 25 % con respecto a sus ortólogos, sin embargo este software no permite la manipulación estricta por parte del usuario para controlar las secuencias que contribuyen a la construcción de la matriz, lo que puede resultar en encuentros erróneos como lo muestra la figura 2.

Figura 2: Ejemplo de falsos positivos obtenidos con el software PSI-BLAST. 

Otra limitante de los métodos de perfiles calificados por matrices de sustitución es que dependen en gran medida de los parámetros del método. En particular la penalización por gap, que corresponde a un valor fijo sin tener en cuenta que un conjunto de secuencias posee regiones muy conservadas (sitios catalíticos) y regiones variables, penalizando la aparición de gaps de igual forma en todas las regiones; las sustituciones, inserciones o deleciones en una región conservada deberían idealmente penalizarse más que en regiones variables, de igual forma, algunas clases de sustituciones deberían penalizarse con diferente relación y valor en una posición u otra. Estas limitantes se ven superadas con el uso del modelo estadístico HMM que denota un alineamiento múltiple variable con penalizaciones por gap dependientes de la posición; ya que en el las penalizaciones son definidas en términos de probabilidad de acuerdo a la información suministrada (secuencias de entrenamiento).

Los HMM descritos por Andréi Markov en 1906 [¹⁶], son una representación estadística extremadamente versátil que se puede utilizar para modelar cualquier conjunto de datos de símbolos discretos unidimensionales. Un HMM describe una serie de observaciones a través de un proceso estocástico "oculto" que cumple con la propiedad de Markov: -Dado un evento i la probabilidad de ocurrencia del siguiente evento j solo depende de la probabilidad condicional P_(i|j) ^.

En 1989 Rabiner [¹⁷] aplicó este modelo estadístico en técnicas de reconocimiento de voz y solo hasta 1994 Krogh y sus colaboradores [¹⁸] aplican el HMM en técnicas bioinformáticas para proteómica realizando una analogía a su aplicación en las técnicas de reconocimiento de voz.

En proteómica el "modelamiento de proteínas" puede ser descrito por el HMM: En esta aplicación las observaciones son representadas por los 20 aminoácidos formadores de una proteína y el modelo HMM es el que por un proceso aleatorio y "oculto" genera las secuencias de aminoácidos, entonces el modelo puede definir una probabilidad de distribución sobre las posibles secuencias de aminoácidos que genere. Un buen modelo de proteínas es aquel que asigna una alta probabilidad de distribución a las secuencias que pertenecen al conjunto de secuencias que modela. En términos biológicos los HMM construidos para familias, dominios o motivos de proteínas describen la estructura primaria de las secuencias con los elementos básicos que caracterizan las moléculas homólogas. Pero, ¿Cómo se construye un HMM para una familia de proteínas?.

3. Arquitectura HMM para proteínas

Consideramos una familia de proteínas con una función celular en común como la actividad deubiquitinadora de las DUBs (deubiquitinating enzyme) UCH (ubiquitin C-terminal hydrolase): La función deubiquitinadora de la familia de secuencias DUBs UCH puede ser caracterizada en función de una secuencia de posiciones en el espacio A1....A5 (figura 3) donde se ubican los aminoácidos -indicados en la figura- con su estructura dentro de la cadena polipeptídica, en la parte superior de la figura 3 y como letras en el alineamiento -parte inferior de la figura- obedeciendo a una probabilidad de distribución sobre los 20 aminoácidos para cada posición en la proteína. En términos generales esta es la definición de un perfil [¹⁹].

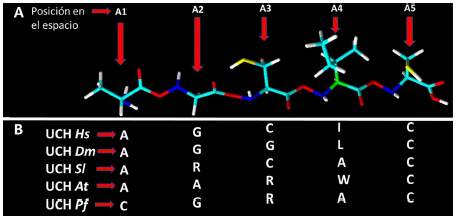
Figura 3: Sitio catalítico Cys de la enzima UCH. A Estructura 3D de fragmento UCH de H. sapienes. B Alineamiento múltiple de secuencias fragmento UCH. *H. sapiens (Hs), D. melanogaster (Dm), S. licopersycum (Sl), A. thaliana (At) y P. falciparum (Pf). 

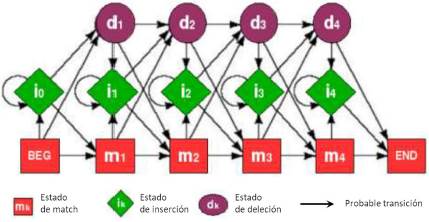
La estructura de un HMM para una familia de proteínas es en términos generales es similar a la de un perfil de secuencias. La línea principal de un HMM contiene una secuencia de M estados los cuales son llamados estados de match, que corresponden a las posiciones de los aminoácidos en proteína o a las columnas en un alineamiento múltiple, M = 4 en el ejemplo de la figura 4. Cada uno de estos estados puede generar una letra x desde un alfabeto de 20 letras (que representan los 20 aminoácidos) de acuerdo a la probabilidad de distribución P(x|mk) donde k es un contador k = 1....M. De la notación P(x|mk) se infiere que cada estado de match (mk) tiene una probabilidad de distribución distinta.

Por cada estado de match (mk) existe un estado de deleción dk que no produce ningún aminoácido y que es un estado alterno para los eventos en los que no hay transición hacia un estado de match (mk), figura 4.

Figura 4: Representación gráfica (grafo) de un perfil HMM para cuatro para secuencias de proteínas. 

Existen también m + 1 estados de inserción i _k - 1 los cuales generan aminoácidos del mismo modo que el estado de match pero con una distribución de probabilidad asociada P(x|i_k). Finalmente, por convención se adiciona un estado de inicio "begin" y un estado final "end" denotados en la figura 4 como BEG y END los cuales no producen ningún aminoácido. Desde cada uno de estos estados, son posibles las transiciones indicadas con flechas a otros estados. Las transiciones entre estados de match o deleción siempre se mueven hacia adelante en el modelo mientras que las transiciones desde un estado de inserción pueden registrar retornos sobre el mismo estado de inserción; en razón a que múltiples inserciones pueden ocurrir en un alineamiento múltiple. La probabilidad de transición desde un estado q a un estado r es denotada como T_(r|q).

Con esta estructura del modelo una secuencia puede ser generada evolucionando de estado a estado en el contador k de acuerdo al modelo (figura 4) de la siguiente forma: Se comienza en un estado de inicio (BEG-begin) donde se puede elegir una transición a un estado m₁, d₁ o i₀ aleatoriamente de acuerdo a las probabilidades T(m₁ |BEG), T(d₁ |BEG) y T(i₀|BEG). Si la transición es hacia m₁ se generará el primer aminoácido x₁ con una probabilidad de distribución P(x|m ₁ ) y una transición al próximo estado acorde con una T(*|m₁) donde * indica el posible próximo estado. Si el próximo estado es el estado de inserción i1 entonces se generará un aminoácido x2 acorde a P(x|i1) y se selecciona el próximo estado de acuerdo a T(*|i₁). Si el próximo paso es al estado de deleción d ₂, no se genera ningún aminoácido y la transición al siguiente estado será de acuerdo a T(*|d₂). Continuando de esta manera llegaremos al estado final END generando una secuencia de aminoácidos x₁,x₂,x₃, ...x _i por la secuencia de estados q₀, q₁, q₂, q₃ ...q _N , q _N + ₁ de acuerdo al modelo. Donde q₀ = m₀ (estado inicial-BEG) y q_N+1 = m_M+1 (estado final-END).

La longitud de N es igual a la longitud de la secuencia de proteína ya que los estados de deleción no producen aminoácidos. Si qi es un estado de match o inserción, se define como el índice de la secuencia x₁ ...x _L de los aminoácidos producidos en el estado q _i . Solamente los aminoácidos emitidos por el proceso q son observables, pero no la ruta o secuencia de estados q, de ahí el calificativo de Modelo "Oculto" de Markov, ya que el proceso por el cual son generadas las cadenas de Markov no son visibles al observador. El proceso de generación de una cadena de Markov dentro del HMM pude ser descrito como la probabilidad de la secuencia de eventos q₀ ....q _N + ₁ deducido desde la secuencia x₁ ...x _L .

Donde el conjunto de P(x _l(i) |qi) = 1 en los casos en que q_i sea un estado de deleción qk. para una descripción formal del HMM [¹⁷]. Esta expresión (Ec. 1) tiene tres limitantes debido a la complejidad de los cálculos:

Primero: Calcular eficientemente la probabilidad de la secuencia de aminoácidos x en un modelo - P(x|modelo) de acuerdo la secuencia observada x = x ₁ x ₂ ....x _N ; es decir la suma de las probabilidades de todas las posibles trayectorias que podrían producir esa secuencia. La limitante radica que el número de rutas en la arquitectura del HMM es exponencial haciéndolo un cálculo de alta complejidad. Ya que en cada tiempo k, k = 1,2...M donde se tienen N estados posibles alcanzables son necesarias N^M operaciones para todas las posibles iteraciones. Sin embargo, este cálculo es posible realizarlo con el uso de una técnica de programación dinámica implementando el algoritmo de avance (for-ward algorithm) que realiza a una velocidad aceptable este cálculo. El resultado de este cálculo es expresado como -logP(secuencia\modelo), que resume la posibilidad de una secuencia dada en el modelo es decir el score de una secuencia para un modelo dado.

Segundo: Encontrar la trayectoria de estados q más probable q = (q₁ q₂ ...q _N + ₁ ) de acuerdo a un modelo para las observaciones x = (x₁ x₂ ....x _N ), ya que el número de cálculos es exponencial -NM- para la determinación de las probabilidades al igual que en el caso anterior. Para este cálculo se usa el algoritmo de retroceso (backward algorithm).

Tercero: Maximizar Prob(x₁ ...x _L , q ₀ ...q _N + ₁ modelo) ajustando la matriz de transición (A)A = (a_ij)_NxN donde a_ij es la probabilidad de transición del estado i al j, el vector de probabilidad de emisión de aminoácidos (B)- uno por cada estado y el vector de probabilidad del estado inicial n logrando con esto que el modelo aprenda; es decir que logre describir de la forma más próxima a la realidad un conjunto de observaciones (el conjunto de secuencias de una familia de proteínas), dominio o motivo de proteínas. Este cálculo se realiza utilizando el algoritmo de Viterbi (Para ver una descripción detallada del desarrollo, matemático de cada uno de estos algoritmos [¹⁷, ²⁰]).

4. Ventajas del HMM en proteómica

La ventaja de usar HMMs en proteómica es que tienen una base pro-babilística formal; donde se puede utilizar la teoría de probabilidad para dirigir los parámetros de anotación de una secuencia. Esta base probabilística permite realizar determinaciones que con los métodos heurísticos comunes -descritos anteriormente- no son permitidas. De esta forma el HMM a diferencia de otros métodos tienen en cuenta en la identificación de secuencias los siguientes parámetros [¹⁸], que desde el punto de vista biológico son relevantes:

1. Algunas posiciones en la secuencia de aminoácidos de una proteína muestran un alto grado de conservación de residuos específicos -el caso de los sitios catalíticos- mientras otras posiciones pueden mostrar considerables variaciones.

2. En determinadas posiciones de la secuencia algunos aminoácidos pueden no estar presentes en algunas proteínas sin que esto afecte la función de la proteína.

3. Las inserciones de aminoácidos en una secuencia de proteína pueden ser permitidas solo en algunas zonas de la proteína mientras que en otras no. Por esta razón los HMM, llamados perfiles HMM en bioinformática, son una fuente muy importante de información de las familias de proteínas [¹⁸]. Actualmente, y gracias a que los HMM poseen parámetros estadísticos definidos lo que permite que sean construidos computacionalmente, sin necesidad de ninguna intervención o curación manual; se han creado bibliotecas de centenares de perfiles HMM que pueden ser usados en la búsqueda de secuencias no anotadas como aproximación de las relaciones funcionales y/o estructurales de una familia de proteínas.

Una de las bases de datos públicas más robustas de perfiles HMM y constantemente actualizada es la base de datos de PFAM (Protein Family Data Base) [²¹, ²², ²³]. La base de datos de PFAM ha sido construida a partir de alineamientos múltiples de secuencias de familias de proteínas utilizando el software CLUSTALW los cuales han sido usados para la construcción de los perfiles HMM con el paquete de software HMMER [²⁴,²⁵] los investigadores del Centro Sanger son los realizadores de esta colección [²¹]. El siguiente paso después de construido el perfil HMM para un conjunto de secuencias (secuencias de entrenamiento), es la búsqueda de secuencias dentro de grandes bases de datos que tengan una alta probabilidad de haber sido generadas por el modelo. Para tal fin es necesario determinar la probabilidad que tiene una secuencia para la trayectoria recorrida a través del modelo para su generación. Sin embargo, para las secuencias que no hacen parte del conjunto de entrenamiento del modelo, es decir para las secuencias que se encuentran en las bases de datos donde se quiere evaluar el HMM, esta trayectoria no se conoce por ello se construye un alineamiento entre la secuencia a evaluar y el modelo HMM -de forma similar a un alineamiento entre dos secuencias- como acercamiento al encuentro de la trayectoria más probable.

Para una secuencia en particular, un alineamiento con el modelo HMM (o con la trayectoria de eventos) se realiza con la asignación de estados para cada residuo en la secuencia, llevándonos un gran número de posibles alineamientos para una secuencia dada [²⁴]. A modo de ejemplo, una secuencia de aminoácidos representada como x1,x₂,x ₃ .... y un HMM representado como m1, m₂, m ₃ ... para los estados de match y i₀, i ₁ , i ₂ ... para los estados de inserción puede tener un alineamiento de la siguiente forma: Un aminoácido x₁ en estado de match m1, dos aminoácidos x₂, x₃ en el estado de inserción i₁, x₄ en el estado de match m₂, x₅ en el estado de match m6 (después de pasar por tres estados de deleción) y así sucesivamente hasta alinear la cadena completa. Para cada posible alineamiento es decir para cada posible trayectoria de estados para formar la secuencia X₁,x₂,x ₃ ... se debe calcular la probabilidad de la secuencia o el score para entonces encontrar el mejor alineamiento, el que tienen el mayor score o probabilidad de cumplir el perfil HMM. Aunque son numerosos los alineamientos que puede tener una secuencia que se evalúa con el modelo HMM es posible calcularlos con algoritmos de programación dinámica como el algoritmo de avance (forward algorithm). El score calculado por el algoritmo de avance (forward algorithm) y normalizado para evitar su dependencia del tamaño de la secuencia encuestada -de forma similar a la función del score en BLAST- es útil para clasificar los encuentros resultantes de la búsqueda de secuencias homólogas con un perfil HMM determinado [¹⁸].

El modelo HMM es muy eficiente para familias de proteínas con bajos porcentajes de identidad y que contienen características funcionales y/o estructurales definidas [²⁶], ya que nos permite cuantificar la forma -para nosotros "oculta"- en que se relacionan las secuencias de una familia de proteínas, desde sus secuencias de aminoácidos-para nosotros la información conocida-.

En conclusión, el método de Modelos Ocultos de Markov (HMM) emerge como una piedra angular fundamental en el campo de la proteómica debido a su capacidad excepcional para modelar patrones y relaciones en secuencias de proteínas. La versatilidad de los HMMs radica en su habilidad para capturar tanto las características globales como las sutilezas locales en las secuencias, permitiendo la identificación de dominios funcionales, la detección de motivos conservados y la predicción de estructuras secundarias. Su aplicación no solo optimiza la anotación y clasificación de proteínas, la evolución molecular y la función biológica. En última instancia, la adopción y desarrollo continuo de los HMMs promete seguir impulsando avances trascendentales en la investigación proteómica y el entendimiento de los procesos celulares y moleculares.