VACUUM MEMBRANE DISTILLATION: MODELING AND ANALYSIS FOR RECOVERY OF ETHANOL FROM ETHANOL/WATER SOLUTIONS

DESTILACIÓN CON MEMBRANAS AL VACÍO: MODELAMIENTO Y ANÁLISIS PARA LA RECUPERACIÓN DE ETANOL DE MEZCLAS ETANOL-AGUA

Omar-Andrés Benavides-Prada¹, César-Augusto Guevara-Lastre¹, Fredy-Wsvaldo Barón-Núñez¹, Crisóstomo Barajas-Ferreira¹,
Rosa-Isela Ortiz-Basurto², Beatriz Torrestiana-Sánchez³ and Carlos-Jesús Muvdi-Nova^1*

¹Universidad Industrial de Santander, Bucaramanga, Santander, Colombia ²Instituto Tecnológico de Tepic, Nayarit, México ³Instituto Tecnológico de Veracruz, Veracruz, México

e-mail: cjmuvdi@uis.edu.co

(Received: Jul. 24, 2012; Accepted: Jan. 09, 2013)

^* To whom correspondence should be addressed

ABSTRACT

A mathematical model was developed to describe the mass and energy transfer in the ethanol separation process by using vacuum membrane distillation. This model is one of the few proposed for studying the ethanol recovery using vacuum membrane distillation; hence, only Soni, Abildskov, Jonsson and Gani (2008) have proposed a more complex model. The mathematical model was validated using fourcase studies reported in literature. The model fairly describes reported data obtained under the following operating conditions: 20 -70ºC, ethanol concentration from 0.25 to 5% w/w, pressure of 2000 -6000 Pa and Reynolds of 50 -2700. The influence of operation conditions and membrane properties on ethanol and water flux, as well as on ethanol concentration in permeate were studied with this validated model by using Statgraphics^® Centurion XVI.I and a factorial experiment design. Pareto analysis showed that operating conditions and membrane properties influence the process variables in different ways. For example, both flux values increase with temperature, pore diameter and porosity; but membrane thickness has a negative effect on water flux (for ethanol flux it was not significant). On the other hand, increasing pressure, pore diameter or porosity decreases permeate ethanol concentration. Last parameter increases with feed ethanol concentration and membrane thickness. In vacuum membrane distillation, the model predicts a permeate ethanol concentration 8.8 times higher than feed concentration, depending on operating conditions and membrane specifications.

Keywords: Vacuum distillation, Membranes, Ethanol, Separation, Mass transfer, Energy transfer, Mathematical model.

RESUMEN

En este trabajo se planteó un modelo matemático para la transferencia de masa y energía durante la etapa de separación de etanol utilizando destilación con membranas al vacío. Este modelo es uno de los pocos propuestos para el estudio de la separación de etanol por destilación con membranas al vacío; solo Soni, Abildskov, Jonsson y Gani (2008) han propuesto un modelo de mayor complejidad que el del presente estudio. El modelo matemático fue validado utilizando cuatro casos de estudio reportados en la literatura. El modelo permite predecir satisfactoriamente los resultados experimentales para condiciones de operación que se encuentren entre 20 - 70ºC, con 0.25 - 5% p/p de etanol en la alimentación, presiones de 2000 - 6000 Pa y Reynolds entre 50 y 2700. Este modelo permitió realizar el análisis de la influencia de parámetros de operación y de diferentes tipos de membranas sobre variables de respuesta como flux de etanol, flux de agua y fracción de etanol en el permeado, utilizando la herramienta Statgraphics® Centurion XVI.I y un diseño experimental factorial. El análisis de Pareto demuestra que dichos parámetros afectan de forma distinta las variables de respuesta del proceso. Los dos valores de flux se incrementan con la temperatura, diámetro de poro y porosidad; el espesor de la membrana tiene un efecto negativo sobre el flux de agua (para el flux de etanol su influencia no es significativa). Por otro lado, un aumento de la presión, el diámetro de poro o la porosidad disminuye la concentración de etanol en el permeado. Éste último se incrementa con la concentración de etanol en la alimentación y el espesor de la membrana. Para la destilación membranaria al vacío, el modelo predice una concentración de etanol en el permeado de hasta 8.8 veces la concentración de alimentación; dependiendo de las condiciones de operación y de las características de la membrana.

Palabras clave: Destilación al vacío, Membranas, Etanol, Separación, Transferencia de masa, Transferencia de energía, Modelos matemáticos.

RESUMO

Neste trabalho é proposto um modelo matemático para a transferência de massa e de energia durante a etapa de separação de etanol utilizando destilação com membranas a vácuo. Este modelo é um dos poucos propostos para o estudo da separação de etanol por destilação com membranas a vácuo; somente Soni, Abildskov, Jonsson e Gani (2008) propuseram um modelo de maior complexidade que o do presente estudo. O modelo matemático foi validado utilizando quatro casos de estudo relatados na literatura. O modelo permite prever satisfatoriamente os resultados experimentais para condições de operação que estão entre 20 - 70ºC, com 0.25 - 5% p/p de etanol na alimentação, pressões de 2000 - 6000 Pa e Reynolds entre 50 e 2700. Este modelo permitiu realizar a análise da influência de parâmetros de operação e de diferentes tipos de membranas sobre variáveis de resposta como fluxo de etanol, fluxo de água e fração de etanol no permeado, utilizando a ferramenta Statgraphics® Centurion XVI.I e um desenho experimental fatorial. A análise de Pareto demonstra que ditos parâmetros afetam de forma distinta as variáveis de resposta do processo. Os dois valores de fluxo aumentam com a temperatura, diâmetro de poro e porosidade; a espessura da membrana tem um efeito negativo sobre o fluxo de água (para o fluxo de etanol sua influência não é significativa). Por outro lado, um aumento da pressão, do diâmetro de poro ou da porosidade diminui a concentração de etanol no permeado. Este último aumenta com a concentração de etanol na alimentação e na espessura da membrana. Para a destilação membranária a vácuo, o modelo prevê uma concentração de etanol no permeado de até 8.8 vezes a concentração de alimentação; dependendo das condições de operação e das características da membrana.

Palavras-chave: Destilação a vácuo, Membranas, Etanol, Separação, Transferência de massa, Transferência de energia, Modelos matemáticos.

At present, the ethanol production is achieved by batch process configurations (due to ethanol inhibition); limiting production rates and increasing the operating costs and environmental impact of the process. The growth in biofuels production (especially anhydrous ethanol) has stimulated the search for new techniques that allow the recovery and concentration of these in a more efficient and profitable manner; membrane technology is one of them.

Amembrane is a semipermeable barrier that prevents direct contact between two phases. The current flowing through the membrane is called permeate or filtrate. While the current that does not manage to go through is known as retentate or concentrate (Geankoplis, 1998). Membrane Distillation (MD) intended to recover alcohols is a technique using porous membranes for the separation of a liquid mixture, wherein the driving force of the process is a partial pressure gradient across the membrane. During the process the volatile components should change phase to pass through the membrane. The major advantage of this technique lies in the possibility to continuously remove ethanol during the production stage of fuel alcohol, thus avoiding inhibition of fermentation by product and thereby increasing production (Lewandowicz, Bialas, Marczewski & Szymanowska, 2011).Additionally, membrane processes are considered clean, simple to operate and linear scaling processes; important factors when considering applications at industrial scale. There are two membrane processes that have been studied for ethanol separation: pervaporation and MD. The main difference between these two techniques is the type of membranes used: pervaporation uses non-porous membranes and MD porous ones. This characteristic allows MD to separate faster the ethanol from ethanol-water solutions (> 100 fold higher).

In MD there are four types of configurations that differ in how the permeate is recovered: Direct Contact Membrane Distillation (DCMD), Air Gap Membrane Distillation (AGMD), Sweeping Gas Membrane Distillation (SGMD) and Vacuum Membrane Distillation (VMD). MD with vacuum and sweeping gas generate greater interest as ethanol separation techniques, since both allow greater flow of permeate with a good concentration of alcohol, compared to other configurations (García, 1998).

MD, intended for the recovery of alcohols (mainly ethanol), is a technique that has scarcely been studied. Studies have focused mainly on the experimental analysis of the technique. To date, only Soni et al. (2008) have proposed one model for the study of ethanol separation using this unit operation. That general model includes 62 equations and 57 parameters, which defines it as a model of high complexity. This complexity lies on the fact that the model takes into account all the occurring phenomena, regardless of the major or minor contribution of these terms in the variation equations describing the process. The aim of this paper is to study the VMD technique through a simplified mathematical model, based on the energy and mass transfer across the membrane for diluted mixtures of ethanol-water. The simplification of the model was done through validation of the hypothesis considered for this application. A finite difference method was used to solve the mathematical model applying the software tool Matlab 6.2 and reported data from literature were used for validation of the model. The program was adapted to flat and tubular membrane geometries. The validated model allowed the analysis of the influence of operating parameters (temperature, pressure, Reynolds, feed rate) and membrane characteristics (porosity, pore diameter, membrane thickness) on response variables such as ethanol flux and water flux as well as on the ethanol permeate concentration, within the ranges of model validation by using the Statgraphics^® Centurion XVI.I.

2. MATHEMATICAL MODEL APPROACH

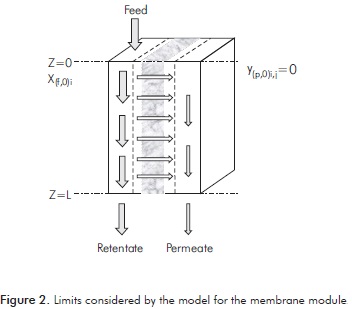
MD is the separation of two or more volatile compounds from a liquid mixture that uses a porous membrane as a physical barrier. The separation occurs because of the partial pressure difference on both sides of the membrane (feed and permeate compartments). Figure 1 represents the distribution of the concentration profiles during the process.

Mass transfer in MD can be described according to the resistance model (Yeom, Lee, Lee & Song, 2002; Bocquet et al., 2006). This model considers that the permeate flux get through three different regions (see Figure 1): the boundary layer of the feeding side, the membrane and the boundary layer of the permeate side. The resistances are set by the inverse of the respective mass transfer coeficient.

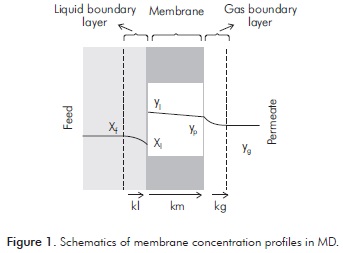
The equations representing mass and energy transfer during the process were defined taking into account the following considerations: 1) steady-state process. 2) The boundary layer is negligible on the permeate side. This consideration is valid due to the low pressure (high vacuum) used during the process; allowing the presence of a gas stream on this side of the membrane to be considered negligible (Soni et al., 2008). In this way, the model considers only the resistance in the boundary layer from the retentate side and inside the membrane. 3) The polarization phenomenon due to temperature is negligible (García, 1998). This phenomenon (analogous to the concentration polarization phenomenon) occurs in processes that involve a phase change across the membrane, generating a temperature gradient in the boundary layer of the retentate side. For this type of application the flux values through the membrane are not sufficiently large (as compared to feed rate) to generate such gradient. 4) The phase change of the volatile compounds occurs at the liquid-membrane interphase (Soni, Abildskov, Jonsson & Gani, 2009). It is therefore considered that the mixture does not enter the membrane. 5) The membrane resistance to the mass transfer is due to the selective layer. In membrane aplications is accepted that the resistance offered by the porous support that holds the membrane is negligeable: The selective layer (membrane) offers the main resistance through the porous media (Bocquet et al., 2006). 6) The mass transfer through the membrane in this process is mainly due to the Knudsen type diffusion. Knudsen number (K_nd) was determined by Equation 1 (Zamora, 1998). For all the operating conditions studied K_nd> 3.2, meaning that there is a predominance of the molecule-membrane wall collisions. This is based on the fact that the membrane pore diameter is considerably smaller than the path length traveled by the molecule, making this type of collisions more important (Geankoplis, 1998; Soni et al., 2009). 7) The flux values of water and ethanol are independent from each other. At this point molecular interactions are negligible between these compounds, due to the low ethanol concentration levels in the feed (Martínez, Florido, Hernández & Prádanos, 2002). 8) It is considered that the membrane is homogeneous; therefore properties are the same throughout the membrane (Martínez et al., 2002).

Where λ is the molecule free path and L is the characteristic length. K_B is the Boltzman number, T is the temperature, P the pressure and δ the molecule diameter.

Mass Balance

For low solute concentration and low velocities (boundary layer conditions), the mass balance for the distillation membrane is defined by the following differential equations (Soni et al., 2009):

Where n_f,k and n_p,k are the molar flux values for each compound in the feed and the permeate side, respectively; z is the length and w is the membrane width.

Mass Transfer Boundary Layer on the Retentate Side

The ethanol flux through the boundary layer on the feed side is represented by the difference between the molar fractions within the liquid (feed) and the liquid membrane interphase.

Where, N_i is the ethanol flux, and xif and x_i1 are the mole fractions within the feed and the liquid-membrane interphase. R_l is the coefficient resistance of the boundary layer to mass transport on the feed supply side.

Where ρ is the molar average density of the ethanol-water mixture and K_l is the mass transfer coefficient at the boundary layer of the retentate side, which is defined by Equation 6 (Bird, Stewart & Lightfoot, 1998).

Where D_ea is the diffusivity of ethanol in water, D_h is the system hydraulic diameter (this parameter depends on membrane geometry: flat or tubular) and S_h is the Sherwood dimensionless number. This dimensionless number is defined by a semi-empirical model that includes the dimensionless Reynolds (Re) and Schmidt (Sc) numbers (Bird et al., 1998; Kamalesh & Winston, 1992; Soni et al., 2008).

For Re < 2100

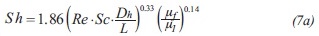
For 2100 < Re < 10000

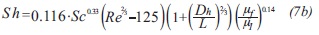
Where L is the length of the hydraulic channel, and µ_f y µ₁ are the dynamic viscosities within the liquid (feed) and the liquid-membrane respectively.

Mass Transfer Through the Membrane

The mass transfer across the membrane is assured by the partial pressure gradient between each side of the membrane, as described in Equation 8.

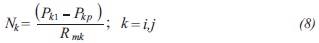
Where N_k is the flux for each component, P_k1 and P_kp are the partial pressures of water and ethanol in the liquid-membrane interphase and the permeate side, R_mk is the coefficient resistance to mass transport of ethanol and water.

Where K_m is mass transfer coefficient through the membrane and M_k is the molecular weight of each component.

Izquierdo-Gil and Jonsson (2003) showed in their work that the Knudsen type diffusive mechanism is the most relevant in MD. For this type of diffusive mechanism, K_m is represented by the following equation (Bandini, Saavedra & Sarti, 1997):

K_m depends on temperature (T), and membrane characteristics, such as: porosity (ε), tortuosity (τ), pore diameter (d_P) and membrane thickness (δ_m). R is the universal gas constant.

The tortuosity (τ) is defined by the following correlation (Soni et al., 2008):

The partial pressures at the membrane-liquid interface P_k1 and the permeate side P_kp may be represented by (Diban, Voinea, Urtiaga & Ortiz, 2009):

Where γ_k is the activity coefficient, γ_k1 and x_k1 are the mole fractions in the liquid-membrane interphase of the permeate side and the feeding side respectively, P_k^s is the saturation pressure, y_kp is the molar fraction in the permeate and P is the pressure at the permeate side.

The activity coefficient for ethanol and water was calculated from the Non-Random Two-Liquid (NRTL) method (Sarti, Gostoli & Bandini, 1993; Tang, Li & Li, 1995).

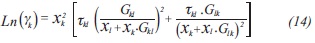
The partial pressures were obtained from the Antoine ratio (Smith, Van Ness & Abbott, 1997). Other physicochemical properties were obtained from Perry's Handbook (Perry & Green, 2008). Matlab 6.2 tool was used to perform the calculations.

Energy Transfer in the Process

The energy balance was set for each segment of the membrane as follows:

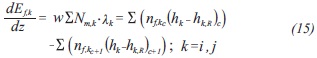
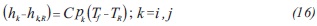
Where n_f,kc and n_f,kc+1 are the molar flux of each component in the feed side, z is the length and w is the membrane width; (h_k-h_k,R) is the enthalpy difference of the component k with respect to a reference point: N_m,kc is the flux of component k; λ_k is the evaporation latent heat of component k; Cp_k is the calorific capacity at constant pressure of component k. The subscript c refers to the segment of membrane that the balance is applied to.

The latent heat of evaporation of each component was calculated based on the following equation (Perry & Green, 2008):

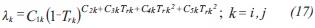
Where, T_rk is the reduced temperature of component k and T_Ck is the respective critical temperature.

The heat capacity of the components were calculated based on the following equation (Perry & Green, 2008):

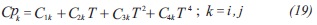
Ethanol density was calculated based on the follow ing equation (Perry & Green, 2008):

The viscosity of the components was determined based on the following equation (Perry & Green, 2008):

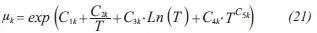
All the physicochemical properties were taken from the Chemical Engineers' Handbook (Perry & Green, 2008). Aqueous solution properties were determined considering the ethanol concentration in the solution (Perry & Green, 2008).

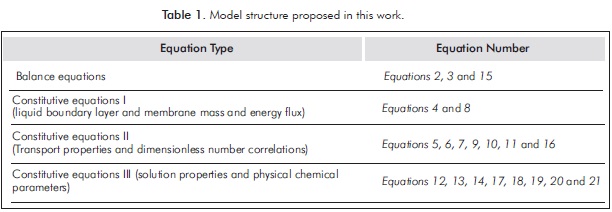
The equations used to establish the mathematical model are summarized in Table 1 and were grouped considering the structure of the model.

The model was developed according to the limits defined in Figure 2. Differential equations were solved using the Runge-Kutta 4. Program entries were the feed ethanol concentration in the retentate side (x_f,0) and the permeate side (y_g,0= 0), the feed rate, the temperature, the hydraulic diameter as well as the length, the porosity and the membrane pore diameter.

3. VALIDATION OF THE PROPOSED MATHEMATICAL MODEL

Four case studies reported in literature were used to validate the mathematical model (Izquierdo & Jonsson, 2003; Sarti et al., 1993; Lawson & Lloyd, 1996; Soni et al., 2008). Table 2 summarizes the major characteristics of the membranes used in this research. It is important to highlight that membranes were hydrophobic, with different geometries, porosities, membrane thicknesses and pore diameters. In addition, case study IV is the result of a mathematical model that used the conditions set for the case study III.

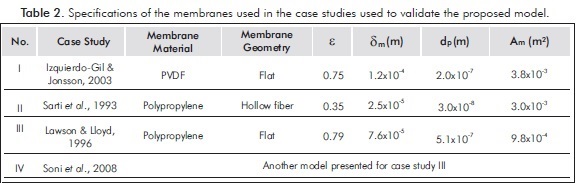
Figures 3 to 6 show a comparison between the experimental data and those obtained from the proposed model, using the conditions reported for each case study.

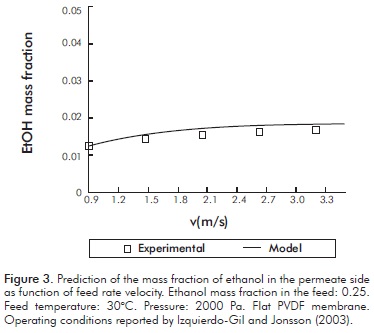
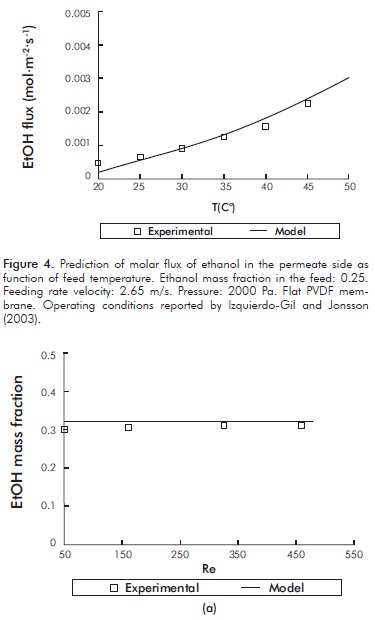
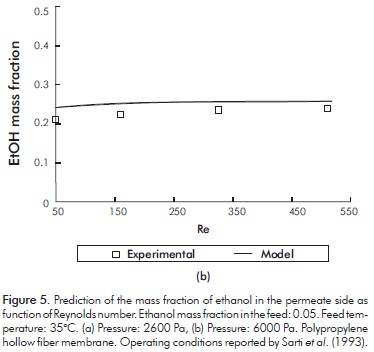
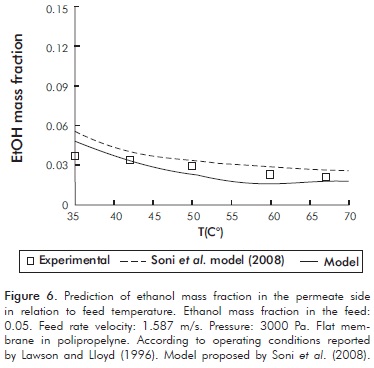
It can be seen from these Figures, that the model fairly predicts the experimental results obtained by different authors with membranes of different geometry and under different experimental conditions.

Additionally, Figure 6 shows that the model proposed in this paper shows a similar behavior to the model reported in literature (Soni et al., 2008). This case study is of the most importance since the degree of complexity of the model proposed in this study is significantly lower.

These results validates the hypothesis considered for the model proposed in this work, mainly the lack of polarization phenomena of concentration and temperature; assumptions that applies to ethanol concentrations below 5% w/w (50 g/L). It should be noted that this concentration range is less than the inhibition concentration reported for S. cervisiae (115 g/L) during the fermentation for ethanol production (Luong, 1985). Therefore, it would be necessary to experimentally validate the model proposed here atethanol concentrations close to the inhibition concentration.

4. INFLUENCE OF OPERATING VARIABLES IN THE MEMBRANE VACUUM DISTILLATION PROCESS

A factorial experimental design was developed using Statgraphics^® Centurion XVI.I to evaluate the effect of the operation variables on the concentration process. Table 3 summarizes the operating parameters and intervals selected for the validation of the model.

Results were analyzed considering flat membrane geometry, in terms of the following response variables: ethanol and water flux through the membrane, as well as ethanol mass fraction in the permeate side.

Ethanol and Water Flux Through the Membrane

Pareto diagrams for ethanol and water flux through the membrane are shown in Figures 7 and 8, respectively.

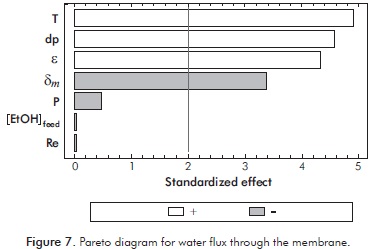
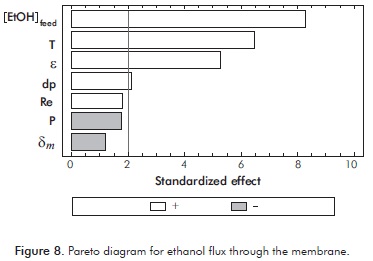
It can be seen from Figures 7 and 8, that only temperature, pore diameter and porosity affect positively the flux values of both, water and ethanol. An increase of temperature favors the growth of both flux values (4180% and 388% for water and ethanol flux respectively) as a result of improved diffusion of these compounds and the increment on vapor pressure at the interface, thereby increasing the pressure gradient on both sides of the membrane. Likely, higher porosity favors permeation flux (1045% and 234% for water and ethanol flux respectively). This can be explained by an increment on the free space inside the membrane, which improves diffusion of solutes through it. Finally, an increase in the pore diameter of the membrane allows increments on the exchange surface of the liquid-membrane interphase generating higher flux values through it (1594% and 55% for water and ethanol flux respectively).

Regarding the other parameters of the process, their significance depends on the type of flux. Thus, the thickness has a negative influence on water flux (-79%). This effect is explained by the higher resistance to water flux found when increasing the trajectory of these molecules on the hydrophobic surface inside the membrane pores. On the other hand, increasing ethanol concentration in the feed, induces higher flux values (1100% higher) due to increments on the ethanol concentration gradient, which improves ethanol transfer through it.

Ethanol Mass Fraction in the Permeate Side

Pareto diagram obtained for ethanol mass fraction in permeate is shown in Figure 9. It can be seen that all parameters considered, except temperature and Reynolds, have a significant effect on this process variable.

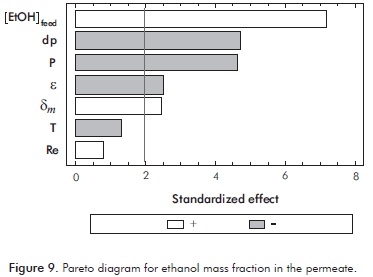
The ethanol fraction in the permeate increases with ethanol concentration in the feed and membrane thickness. This is due to the fact that these parameters improve the passage of ethanol at expenses of water transport through the membrane. As was previously noted, increments on the ethanol concentration in the feed increase the concentration gradient, accelerating the transport of ethanol through the membrane (1429% 0.3 higher). Interestingly, an increased thickness of the membrane would hinder the passage of water (major compound in the feed), favoring the ethanol concentration in the permeate side (86% higher), due to an increased permeation resistance without significantly affecting the flow of ethanol.

Furthermore, an increase in the pore diameter, the porosity of the membrane and pressure in the permeate side affect the concentration process (-73, -48 and -72% respectively). These three parameters improve total flux, from which water is the major component, thereby decreasing the ethanol concentration. Accordingly, it can be concluded that the operating conditions and membrane specifications affect the response of the process variables and hence the performance in different ways.

In addition, the membrane mass transfer resistance was in all cases, at least 2x10⁴ fold higher than the liquid boundary layer mass transfer resistance (in some cases over 5.8x10⁴). This confirms the importance of membrane characteristics in the vacuum MD process.

Figure 10 shows ethanol concentrations and total flux values in the permeate side for a flat membrane, predicted by the proposed model within the validated operating ranges (summarized in Table 2), according to a factorial experimental design.

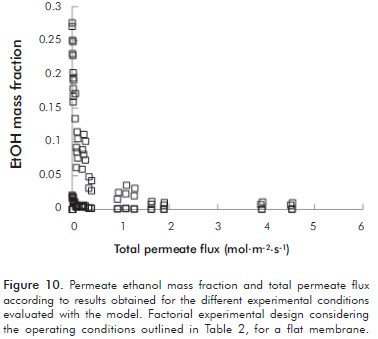
It is clear from this Figure that depending upon the conditions under which the process is carried out we can obtain higher values of total permeate flux at low ethanol concentrations. Otherwise, lower overall flux values are obtained at high ethanol concentrations. Likewise it can be seen that for the two ethanol concentrations on the feedtested (2.5x10^-3 - 5.0x10^-2 w/w ethanol) it is possible to get 8.8 times more concentrated permeates, with flux 100 times bigger than those obtained by pervaporation. These results indicate that MD process is an alternative that would allow the separation of ethanol produced by using less membrane surface (regarding pervaporation). In addition, this technique, when integrated in a production and recovery scheme, maximizes the productivity of the process by removing the produced ethanol.

5. CONCLUSIONS

• A mathematical model for concentration of ethanol-water dilute mixtures by VMD was successfully validated. The model fairly fitted experimental data for low ethanol concentrations (0.25 - 5% w/w), moderate temperatures (20 - 70°C), pressures between 2000 and 6000 Pa and Reynolds between 50 and 2700. These results confirm that polarization phenomena are negligible under these operating conditions; reducing complexity of the model and increasing the speed of calculation.

• Furthermore, it was found that the Knudsen diffusive phenomenon adequately described concentration process during VMD at low concentrations and moderate temperatures. In order to broaden the range of validation of this model, analysis of turbulent flow regimes, applications with less vacuum and analysis with real samples (from fermented solutions) will be considered in future research work.

• Finally, the analysis of the influence of the operating parameters and properties of the membrane on the response variables such as ethanol flux, water flux and ethanol mass fraction in the permeate showed that, in addition to ethanol removal, the membrane vacuum distillation would allow for a 8.8 times increase on ethanol concentration in a single stage, with flux 100 fold higher than those obtained by pervaporation. Such flux values decrease the membrane surface required for the ethanol separation, which is necessary to increase the productivity of the ethanol production process in an integrated continuous production - recovery scheme.

ACKNOWLEDGEMENTS

The authors thank the Vicerrectoría de Investigación y Extensión of Universidad Industrial de Santander, the Departamento Administrativo de Ciencia, Tecnología e Innovación -COLCIENCIAS (Colombia); the Instituto Tecnológico de Veracruz; the Instituto Tecnológico de Tepic and the Consejo Nacional de Ciencia y Tecnología CONACYT (Mexico) for supporting this study registered under the project title: Application of membrane technology for the production of anhydrous bioethanol from fermentation juices of cassava starch. (VIE9409 code).

REFERENCES

Bandini, S., Saavedra, A. & Sarti, G. C. (1997). Vacuum membrane distillation: Experiments and modeling. AIChE J., 43(2), 398-408.         [ Links ]

Bird, R., Stewart, W. & Lightfoot, E. (1998). Fenómenos de transporte: Un estudio sistemático de los fundamentos de transporte de materia, energía y cantidad de movimiento. (2da edición). México: Reverte.         [ Links ]

Bocquet, S., Gascons-Viladomat, F., Muvdi-Nova, C., Sanchez, J., Athes, V. & Souchon, I. (2006). Membranebased solvent extraction of aroma compounds: choice of configurations of hollow fiber modules based on experiments and simulation. J. Memb. Sci., 281(1-2), 358-368.         [ Links ]

Diban, N., Voinea, O. C., Urtiaga, A. & Ortiz, I. (2009). Vacuum membrane distillation of the main pear aroma compound: experimental study and mass transfer modeling. J. Memb. Sci., 326(1), 64-75.         [ Links ]

García, M. (1998). Destilación en membranas de disoluciones acuosas de alcoholes. Tesis Doctoral, Departamento de Física aplicada I, Facultad de Ciencias físicas, Universidad Complutense de Madrid, Madrid, España, 197pp.         [ Links ]

Geankoplis, C. J. (1998). Procesos de transporte y operaciones unitarias. (3ra edición). México: Continental.         [ Links ]

Izquierdo-Gil, M. A. & Jonsson, G. (2003). Factors affecting flux and ethanol separation performance in vacuum membrane distillation (VMD). J. Memb. Sci., 214(1), 113-130.         [ Links ]

Kamalesh, K. & Winston, W. S. (1992). Membrane Handbook. (2da. edición). New York: Chapman & Hall.         [ Links ]

Lawson, K. W. & Lloyd, D. R. (1996). Membrane distillation I. Module design and performance evaluation using vacuum membrane distillation. J. Memb. Sci., 120(1), 111-121.         [ Links ]

Lewandowicz, G., Bialas, W., Marczewski, B. & Szymanowska, D. (2011). Application of membrane distillation for ethanol recovery during fuel ethanol production. J. Memb. Sci., 375(1-2), 212-219.         [ Links ]

Luong, J. H. T. (1985). Kinetics of ethanol inhibition in alcohol fermentation. Biotechnol. Bioeng., 27(3), 280-285.         [ Links ]

Martínez, L., Floriíaz, F. J., Hernández, A. & Prádanos, P. (2002). Characterizations of three hydrophobic porus membranes used in distillation. Modeling and evaluation of their water vapor permeabilities. J. Memb. Sci., 203: 15-27.         [ Links ]

Perry, R. H. & Green, D. W. (2008). Perry's Chemical Engineers' Handbook. Tomo II. (8th Ed). México: McGraw-HILL.         [ Links ]

Sarti, G., Gostoli, C. & Bandini, S. (1993). Extraction of organic components from aqueous streams by vacuum membrane distillation. J. Memb. Sci., 80(1), 21-33.         [ Links ]

Smith, J. M., Van Ness, H. C. & Abbott, M. M. (1997). Introducción a la termodinámica en ingeniería química. (5ta. edición). México: McGRAW-HILL.         [ Links ]

Soni, V., Abildskov, J., Jonsson, G.& Gani, R.(2008). Modeling and analysis of vacuum membrane distillation for recovery of volatile aroma compounds from black currant juice. J. Memb. Sci., 320(1-2), 442-455.         [ Links ]

Soni, V., Abildskov, J., Jonsson, G. & Gani, R. (2009). A general model for membrane-based separation processes. Comp. & Chem. Eng., 33(3), 644-659.         [ Links ]

Tang, Y., Li, Z. & Li, Y. (1995). Salting effect in partially miscible systems of n-butanol-water and butanone-water 2. An extended Setschenow equation and its application. Fluid Phase Equilibria, 105(2), 241-258.         [ Links ]

Yeom, C. K., Lee, S. H., Lee, J. M. & Song, H. Y. (2002). Modeling and evaluation of boundary layer resistance at feed in the permeation of VOC/N2 mixtures through PDMS membrane. J. Memb. S., 204(1-2), 303-322.         [ Links ]

Zamora, M. (1998). Termo I: Un Estudio de los Sistemas Termodinámicos. Manuales Universitarios. Secretariado de Publicaciones: Universidad de Sevilla.         [ Links ]