Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista U.D.C.A Actualidad & Divulgación Científica
Print version ISSN 0123-4226
rev.udcaactual.divulg.cient. vol.15 no.1 Bogotá Jan./June 2012
CIENCIAS AGROPECUARIAS - Artículo Científico
MODELO DINÁMICO PARA ESTIMAR LA CAPACIDAD DE CARGA DE CUERPOS DE AGUA CON PISCICULTURA
DYNAMICAL MODEL TO ESTIMATE CARRYING CAPACITY IN RESERVOIRS WITH FISH FARMING
Javier Riascos1, Diana Díaz2, Luis Beltrán3, Francisco Gutiérrez4
1 Físico, M.Sc. Matemática Aplicada, javier.riascos@utadeo.edu.co
2 Física, M.Sc. Meteorología dianac.diaz@utadeo.edu.co
3 Biólogo M.Sc. Biología luis.beltran@utadeo.edu.co
4 Biólogo Marino, Ph.D. francisco.gutierrez@utadeo.edu.co
Rev. U.D.C.A Act. & Div. Cient. 15(1): 135 - 145, 2012
RESUMEN
Se propone un modelo dinámico para estimar la capacidad de carga en embalses con actividad acuícola intensiva. La propuesta fue obtenida generalizando el modelo tradicional de balance de fósforo de Dillon y Rigler, formulado en 1974, para cultivo en jaulas en embalses. El modelo es un sistema de dos ecuaciones diferenciales ordinarias que determinan la evolución temporal de la biomasa (Bm) de los peces y del fósforo disuelto (P). El planteamiento tiene en cuenta parámetros adicionales, como el fósforo proveniente de fuentes externas, variaciones en el régimen de alimentación, y la influencia de éstos al proceso de eutrofización del ecosistema. Se demuestra que el modelo de Dillon & Rigler es un caso particular del nuevo modelo tomando una tasa de alimentación constante y se generó una interfaz gráfica, utilizando el programa Mathematica7 ®, para simular diferentes escenarios de cultivo. El trabajo realizado pretende contribuir a la toma de decisiones para la adecuada planeación y operación de proyectos piscícolas, en embalses y en otros cuerpos de agua lénticos.
Palabras clave: Piscicultura, balance ecológico, capacidad de carga, modelo matemático.
SUMMARY
We propose a dynamical model to estimate the carrying capacity of artificial water bodies with intensive fish farming. The dynamical model builds from the traditional phosphorus budget model by Dillon & Rigler (1974) on cage fish farming on artificial reservoirs. The model consists of two ordinary differential equations. The model determines biomass, fish and phosphorus temporal evolution. The model takes into account additional parameters such as phosphorus loading from external sources, variations on feeding regimes and the further influence of these parameters on the ecosystem eutrophication. Results show that the Dillon & Rigler model is a particular case of the new model by taking a constant feeding rate. In addition, an interactive graphical application was developed to simulate several scenarios, using the software Mathematica 7 ®. This work contributes to fish farming planning and management on artificial reservoirs and other water bodies.
Key words: Pisciculture, ecological balance, carrying capacity, mathematical models.
INTRODUCCIÓN
La expansión demográfica del hombre y sus requerimientos, en términos de aprovechamiento de los recursos, han modificado las condiciones naturales de los ecosistemas, en todas las escalas. El reporte Millenium Ecosystem Assessment (2005), por ejemplo, estima que, aproximadamente, el 60% de los servicios que prestan los ecosistemas están siendo usados de manera no sostenible. Esta degradación influye en la disponibilidad de agua dulce, la pesquería, la piscicultura, la purificación del agua y el aire, la regulación del clima regional y local, las amenazas naturales y las pestes.
La acuicultura es un modelo. Están comprobados los impactos negativos sobre los bienes y los servicios de los ecosistemas acuáticos, como consecuencia de la alteración de la calidad de aguas adyacentes, la introducción de especies exóticas y la utilización de alimentos procesados o concentrados. Estos factores contribuyen al enriquecimiento del agua con nutrientes aumentando su productividad, lo que se traduce en una proliferación de algas y de otros organismos fotosintéticos, que conducen al proceso de eutrofización del cuerpo de agua (Black, 2001; Magill et al. 2006).
En particular, el sistema de cultivo intensivo es uno de los más utilizados en el mundo y el que más perjudica el ambiente. Esta metodología consiste en el uso de jaulas flotantes sobre cuerpos de agua (lagos, embalses) o estanques en tierra, donde la alimentación se realiza de forma artificial, a través de bolitas de concentrado, con altos contenidos de fósforo y de nutrientes (Beveridge, 1986; Morales et al. 2005). En Colombia, las pérdidas económicas que genera este método en el cultivo de tilapias oscilan entre el 30 y el 40% de la producción (Morales et al. 2005), debido, en gran medida, a la falta de control y al consecuente detrimento de la calidad del agua y su efecto sobre la salud de los peces. En la acuicultura, la determinación de la capacidad de carga es un requisito fundamental. Este concepto se refiere al número máximo de individuos de la población cultivada que el ambiente puede soportar en un periodo de tiempo, teniendo en cuenta las limitaciones de los factores físicos y ambientales. La correcta evaluación o estimación de esta cantidad permite calcular, con anterioridad, el potencial productivo de un cuerpo de agua, para su eventual uso en piscicultura y ajustar los procedimientos de operación, para evitar el deterioro de la calidad del agua (Bottom, 1997; Stickney, 2003).
Los modelos matemáticos que se han desarrollado para la estimación de la capacidad de carga buscan mantener ciertos parámetros ambientales, considerados como críticos, dentro de unos límites preestablecidos y aceptables, desde el punto de vista de la calidad del agua y el sistema bentónico asociado (Findlay & Watling, 1997; Cromey et al. 2002; Stigebrandt et al. 2004; Brigolin et al. 2009).
El modelo más ampliamente utilizado, para el caso particular de piscicultura intensiva, es el propuesto por Beveridge (1986), que se basa, a su vez, en los resultados de los modelos de Vollenweider (1968) y de Dillon & Rigler (1974).
Vollenweider (1968) propuso un modelo para la estimación de la concentración de nutrientes en el agua de los lagos, basado en el principio de conservación de la masa; Vollenweider correlacionó las concentraciones de varios nutrientes con variables indicadoras de procesos de eutrofización, como cambios en Clorofila a, transparencia, entre otros. Los resultados obtenidos a partir de este modelo y de estudios posteriores (Schindler, 1971, 1974; Schindler & Fee, 1974) confirmaron al nitrógeno y al fósforo como los principales nutrientes limitantes en sistemas acuáticos; sin embargo, el contenido de fósforo tiene mayor influencia por las siguientes razones: 1) en pequeñas cantidades es suficiente para estimular significativamente la productividad y aumentar el grado de eutrofización; 2) las reservas gaseosas de fósforo en la atmósfera son menores en comparación con las de nitrógeno u otros elementos como el carbono y el hidrógeno (Vallentyne, 1974); 3) su solubilidad es baja y se asocia fácilmente con los metales para posteriormente precipitarse y, 4) gran parte es adsorbido por la materia orgánica en la superficie y consumido por el fitoplancton, que al incrementar su biomasa ayuda a disminuir los niveles de luz y de oxígeno, afectando la calidad del agua (Sonzogni et al. 1982).
Dillon & Rigler (1974) utilizaron el principio de balance de masa del fósforo de Vollenweider (1968) y definieron una serie de parámetros físicos y ambientales, de más fácil medición, para hallar una expresión para la concentración de P, disuelto en estado estacionario. El modelo ha sido aplicado y validado, tanto en zonas templadas como en tropicales (Dillon et al. 1993; Buyukcapar & Alp, 2006).
Teniendo en cuenta que el fósforo es el factor limitante de un cuerpo de agua, Beveridge (1986) aplicó el modelo de Dillon & Rigler para determinar la capacidad de carga con piscicultura intensiva, mediante la relación de esta cantidad con la concentración máxima admisible de P. Sus resultados han sido aplicados en gran cantidad de lagos y de cuerpos de agua, con piscicultura intensiva (Pulatsü, 2003; Buyukcapar & Alp, 2006).
A pesar de su extensa aplicación, estos modelos carecen de una característica importante y es la descripción explícita con el tiempo, ya que en ellos se propone una solución en estado estacionario. Teniendo en cuenta que las variables y los parámetros pueden presentar cambios con el tiempo (flujos crecientes/ decrecientes de fósforo, aumento en la alimentación de los peces, crecimiento/muerte de los peces, entre otros aspectos), estos modelos reducen la capacidad predictiva y la posibilidad de optimizar la productividad de los proyectos piscícolas, en forma continua (Canosa et al. 2008).
En este artículo, se propone y formula un Modelo Dinámico de Capacidad de Carga (MDCC) para piscicultura intensiva, teniendo en cuenta el comportamiento en el tiempo de la biomasa de producción y la concentración de fósforo, de un embalse o cuerpo de agua, basado en el principio de balance de fósforo de Vollenweider. Adicionalmente, se diseña una interfaz que facilita el ingreso de los parámetros, condiciones iniciales del sistema y la simulación de diferentes escenarios de predicción y de estimación de la capacidad de carga. Con estas herramientas de modelado y de simulación será posible tomar decisiones que, con mayor certeza y flexibilidad, permitan minimizar el impacto ambiental.
MATERIALES Y MÉTODOS
Para la elaboración del modelo dinámico de capacidad de carga, en primer lugar, se realizó un estudio detallado de la propuesta original de Vollenweider (1968), de Dillon & Rigler (1974) y de Beveridge (1986). Se estudiaron las relaciones de las variables básicas involucradas: concentración de fósforo [P] y producción (biomasa o número de individuos) de peces Bm, mediante la ecuación de balance de fósforo y expresiones para las concentraciones de fósforo en el alimento y en los peces, suponiendo piscicultura intensiva. Dado que la ecuación de balance de fósforo es una ecuación diferencial para la variación de P en el tiempo (Vollenweider, 1968), el formalismo matemático adecuado para describir las variables de interés ([P] y Bm), en el tiempo, consiste en un sistema de dos ecuaciones diferenciales ordinarias para las variables en cuestión, en función del tiempo. Esto se logró a partir de la generalización de la ecuación de balance de fósforo a un caso no estacionario, es decir, a un caso de variación de P (derivada de P no nula). Matemáticamente, se demostró que la propuesta de Dillon & Rigler y de Beveridge son casos particulares del nuevo modelo. Con esta validación, se programó en Mathematica 7 ®, el código necesario para crear un simulador con una interfaz gráfica apropiada y, finalmente, se compararon los resultados con dos estudios previos realizados en cuerpos de agua con piscicultura intensiva.
RESULTADOS Y DISCUSIÓN
El Modelo de Dillon - Rigler y Beveridge: En la siguiente descripción se denomina sistema (o cuerpo de agua), al conjunto columna de agua + sedimentos. El modelo de Dillon & Rigler (1974) es utilizado por Beveridge (1986), para la estimación de la capacidad de carga de cuerpos de agua, que van a ser utilizados para el cultivo intensivo; considera la concentración de fósforo [P] (en kg/m3) en la columna de agua, como el principal factor limitante de la productividad y además realiza las siguientes consideraciones:
1ª suposición: El fósforo entrante se disuelve instantánea y uniformemente en todo el cuerpo de agua. Para que P cumpla con esta suposición, se debe medir como un promedio espacial y temporal en todo el cuerpo de agua y durante todo el año.
La ecuación de balance de masa del fósforo presente en el cuerpo de agua se puede expresar como sigue:

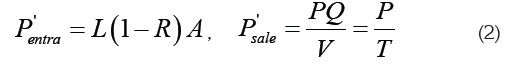
Dónde, L es el flujo de entrada de fósforo al sistema (kg/ (m2*año)), A es el área superficial del cuerpo de agua (m2), Q es el caudal de salida del agua (m3/s), V es el volumen del cuerpo de agua (m3) y T es el tiempo de descarga dado por el cociente entre V y Q, T=V/Q (años). R es la fracción de fósforo entrante perdida por acumulación en los sedimentos. Se puede determinar, experimentalmente, midiendo la entrada y la salida medias anuales de [P]: [Pin] y [Pout], mediante: R=1-[Pout]/[Pin] (Beveridge, 1986). Si no se conocen los valores en campo es posible utilizar diferentes modelos empíricos, obtenidos a partir de ajustes estadísticos a datos recogidos en diferentes cuerpos de agua. La expresión más utilizada en la literatura es la que se reporta para lagos naturales: R =1/ (1+ 0747(1/ T)0.507 ) (Larsen & Mercier, 1976; Beveridge, 1986).
2ª suposición: El sistema está en estado estacionario, es decir, P, [P] y L son constantes, por tanto, de (1) se tiene que Psale=Pentra, luego igualando las expresiones de (2), teniendo en cuenta que [P] = P/V, V=Az con z la profundidad media del cuerpo de agua (m), resulta:

Esta es la esencia del modelo de Dillon y Rigler. Como se mencionó previamente, Beveridge (1986) utiliza este modelo para estimar la capacidad de carga de cuerpos con piscicultura intensiva. Él supone que la ecuación (3) también se satisface para la concentración de fósforo presente en la columna de agua, producto de la actividad piscícola proveniente del alimento no ingerido y los excrementos de los individuos (fósforo excedente) [Pexc]:

Donde, Lexc es el flujo de entrada a la columna de agua del fósforo excedente (kg de fósforo/(m2*año)) y Rfish es la fracción de fósforo proveniente de los cultivos piscícolas perdida en los sedimentos (Beveridge, 1986; Buyukcapar & Alp, 2006).
El valor límite o admisible de [Pexc], se estima a partir de las concentraciones final e inicial [Pfinal] y [Pinicial], respectivamente, donde [Pfinal] es la concentración máxima admisible de fósforo posterior a la cosecha (que para embalses tropicales tiene un valor de 100mg/m3 y para embalses templados de 60mg/m3) y [Pinicial] es la concentración de fósforo medida y promediada en la columna de agua en momentos previos al inicio de toda actividad de piscicultura:

Beveridge (1986) propuso estimar la producción de biomasa anual o capacidad de carga (CC), a partir de la razón en tre la rapidez de entrada a la columna de agua del fósforo excedente (Pexc en unidades de kg de Pexc /año) y el fósforo descargado al sistema producto de los cultivos por tonelada de pez producida (Pexc en unidades de kg de Pexc /Tonelada de pez producida), es decir, CC = Pexc / Pexc (en unidades de Ton de pez/año).
Pexc está dado por Pexc = Lexc A y Pexc, que se obtiene a partir del fósforo que entra al sistema como alimento y el fósforo que sale en forma de biomasa del pez.
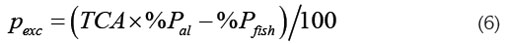
Donde, %Pal es el porcentaje de fósforo contenido en el alimento suministrado, %Pfish el porcentaje de fósforo contenido en los peces, el cual, se toma como constante, medido al final de la cosecha (Beveridge, 1986). TCA es la tasa de conversión alimenticia del alimento suministrado, definida como el cociente del alimento suministrado y el aumento en biomasa del pez:
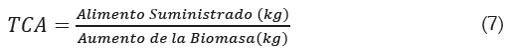
La relación muestra que a menor TCA más efectivo es el alimento en términos del peso del individuo. En general, para las especies de interés comercial los valores de TCA varían entre 1,4 y 3,0 (Beveridge, 1986).
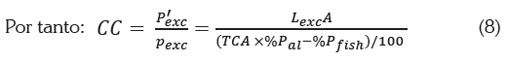
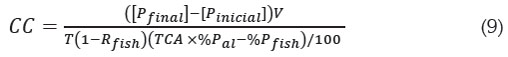
Modelo dinámico para la biomasa de peces y fósforo disuelto (MDCC): El modelo que se propone en este artículo involucra las variables de fósforo disuelto P y la Biomasa de los peces en cultivo Bm. El modelo, se planteó como un Problema de Valor Inicial PVI y consiste en un sistema de dos ecuaciones diferenciales ordinarias con variable independiente t y variables dependientes P y Bm, junto con los valores de estas variables, en algún tiempo t = 0 (condiciones iniciales). Al solucionar el sistema, se obtienen las curvas de P y Bm en función del tiempo t, con las cuales, se puede encontrar [Pf] y Bm, al cabo de un periodo de tiempo determinado.
Ecuación Diferencial para la Biomasa Bm: La variación de la cantidad de biomasa Bm de peces cultivados en el cuerpo de agua en un tiempo t (o derivada de Bm respecto a t: dBm/dt) es directamente proporcional al flujo de entrada de alimento IA (kg alimento/día) e inversamente proporcional al factor que de este alimento el pez efectivamente transforma en Biomasa (TCA), por tanto:

La condición inicial para la biomasa está dada por Bm(0)= bm alevino N , con N, el número de alevinos que ingresan al sistema y bmalevino, el peso del alevino que se cultiva. Bajo esta aproximación no se está teniendo en cuenta la mortalidad de los peces, es decir, que el número de individuos en cualquier tiempo es igual al número inicial de alevinos N. De otra forma habría que considerar otras variables que afectan la mortalidad/supervivencia de los individuos, como la concentración de oxígeno disuelto o la turbidez. En el modelo propuesto no se tienen en cuenta estas variables o simplemente son parámetros constantes con valores adecuados, para asegurar la supervivencia de los individuos.
Para elegir el parámetro IA existen dos opciones: la primera consiste en tomar un valor constante (como en Beveridge, 1986) y estimarlo a partir del promedio del alimento suministrado en un determinado tiempo. La segunda opción es tomar IA variable; en este caso, se tienen en cuenta las tablas de alimentación utilizadas en piscicultura, en las cuales, se sugiere que la cantidad diaria de alimento a suministrar a cada individuo sea un porcentaje o fracción c (llamado Parámetro de Alimentación) de la biomasa del individuo, es decir, IA = cBm, c varía con el tiempo de cultivo, ya que depende de las condiciones fisiológicas, edad del pez y del tipo de alimento.
Ecuación diferencial para el fósforo disuelto P: Esta ecuación describe la tasa de variación de la cantidad de fósforo disuelto P en la columna de agua. Para obtenerla, se utiliza la ecuación de balance de masa del fósforo (1) y las consideraciones descritas a continuación.
Entrada de fósforo: El fósforo que entra al sistema proviene de dos fuentes: la primera, del flujo de entrada de fósforo al sistema proveniente de otras fuentes diferentes a la piscicultura, llamada fotros (kg de fósforo/día) y, la segunda, del flujo de entrada del fósforo proveniente del alimento al sistema, llamada fal (kg de fósforo/día). fal es entonces proporcional a IA y a %Pal.

Una fracción Rfish del fósforo entrante se sedimenta y la otra (1 - Rfish) permanece en la columna de agua.
Con estas consideraciones, la rapidez de entrada del fósforo viene dada por:
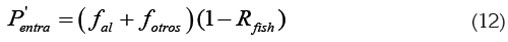
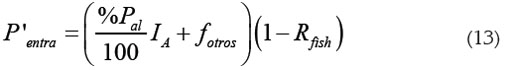
Salida de fósforo: La salida de fósforo está dada por la suma de dos términos: el de descarga del cuerpo de agua y el fósforo presente en el alimento, que es consumido por los peces. Se puede expresar como el producto entre %Pfish y dBm/dt y todo el término debe estar multiplicado por el factor (1 - Rfish), porque el pez sólo tiene acceso al fósforo, que permanece en la columna de agua.
Con estas consideraciones Psale está dada por:
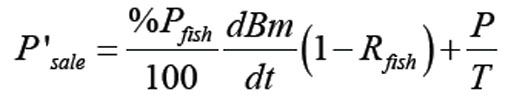
La ecuación diferencial para el fósforo P resulta de la resta entre Pentra y Psale:
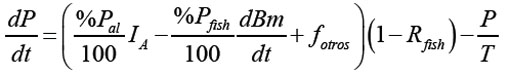
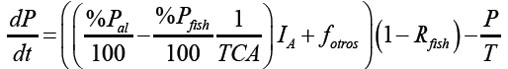
La condición inicial para P está dada por P(0) = [P](0) V .
La cantidad que interesa conocer es la concentración de fósforo en función del tiempo: [P](t). Una vez que se solucione para P, la concentración se puede obtener como
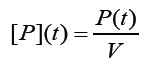
El MDCC lo constituyen las ecuaciones (10) y la ecuación (14), junto con las condiciones iniciales de ambas variables. Aspectos matemáticos relevantes de este sistema es que la ecuación para Bm es independiente de la ecuación para P y se puede solucionar analíticamente, por medio del método de separación de variables. La ecuación para P, a su vez, puede depender de la primera, en caso que se escoja para IA la expresión dependiente de Bm. En el otro caso, si IA se escoge constante (aproximación que se tomará en el presente trabajo siguiendo a Beveridge), la ecuación para P queda desacoplada de la ecuación para Bm. Se puede demostrar que en este caso la solución para P(t), independiente de los valores de las condiciones iniciales y parámetros, tiende a un valor de equilibrio Peq para valores grandes de t.
El fósforo excedente y el fósforo de otras fuentes en el modelo dinámico: En el modelo de Beveridge (1986), [Pexc] es necesaria para la estimación de la capacidad de carga. En el modelo propuesto, se puede plantear una ecuación dinámica para esta variable y para la variable Potros, lo que permite comparar los modelos. Se parte del hecho que el fósforo total es la contribución de ambos tipos de fósforo:


Donde, Potros es el fósforo disuelto en la columna de agua proveniente de fuentes distintas a la actividad piscícola (kg de fósforo).
Teniendo en cuenta la ecuación (14), se obtienen las siguientes expresiones, para las tasas de cambio de Potros y Pexc:
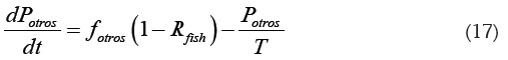
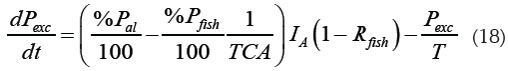
Las condiciones iniciales para estas ecuaciones corresponden a [Potros](0) y [Pexc](0) al iniciar el cultivo.
Una medición en el cuerpo de agua del fósforo corresponde a [P]. En ese caso es difícil saber en cuánto contribuye cada tipo de fósforo al total; sin embargo, se puede conocer cuando la medición se lleva a cabo antes del inicio de cualquier actividad de piscicultura. En este caso, el valor medido para [P] corresponde a [Pinicial] (el valor de [P] medido antes del inicio de la actividad piscícola, según el modelo de Beveridge)y es igual a [Potros](0), ya que la contribución de [Pexc] es nula en ausencia de piscicultura.
Teniendo en cuenta la ecuación (18), se puede definir una tasa de ingreso de fexc, que es la contribución del alimento suministrado al fósforo del sistema:
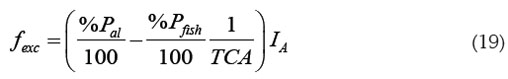
Así, la ecuación para Pexc, se puede escribir como:
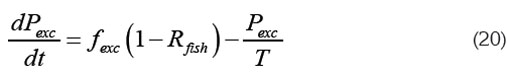
En cuanto al fósforo de otras fuentes, ecuación (17), se puede estimar fotros, suponiendo que el sistema se encontraba en equilibrio en los momentos previos al inicio de la actividad. Esto es admisible si se supone una entrada constante de fósforo (fotros constante) y un tiempo suficientemente largo para asegurar el estado de equilibrio. Entonces, la tasa de cambio de Potros es nula y como P=Potros=Pinicial tenemos de la ecuación (17):

Se interpreta este valor como la entrada de fósforo necesaria para igualar la salida, debido a la descarga hidrológica del cuerpo de agua y así mantener constante la concentración de fósforo, en una situación sin actividad de piscicultura.
La capacidad de carga en el modelo dinámico y equivalencia con el modelo de Beveridge: La capacidad de carga CC, tal como se define en el modelo de Beveridge (1986) (9), corresponde a la producción anual de biomasa de peces cultivados, de tal manera que la concentración [Pexc] sumado a [Pinicial] sea la concentración máxima admisible [Pfinal].
En el modelo MDCC, el cálculo de CC se realiza siguiendo los siguientes pasos o suposiciones:
1) Se modela una situación de inicio de la actividad de piscicultura. En este caso, el valor inicial para [P] corresponde a [Pinicial] y fotros viene dado por (21). Suponiendo, además, que se van a cultivar N alevinos de peso bmalevinos, las condiciones iniciales del MDCC son:
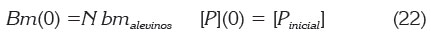
2) Se supone IA (tasa de alimentación) constante, como en Beveridge (1986). Esto asegura que haya una solución de equilibrio para [P]; además, permite solucionar la ecuación (13) para Bm lo que da un crecimiento lineal:

3) Se fija como solución de equilibirio para [P] el máximo permitido [Pfinal], que se supone se consigue en un tiempo de equilibrio teq. En este instante, la tasa de variación de P es nula (ecuación 11):
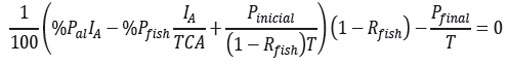
Con esta ecuación, se despeja IA, cuyo valor se interpreta como el necesario para lograr el máximo admisible [Pfinal] para la concentración de P en estado de equilibrio:
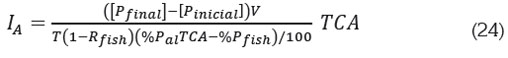
La capacidad de carga es el crecimiento de la biomasa por año, dado este valor de la tasa de alimentación; por (22) y (23) viene dada por:
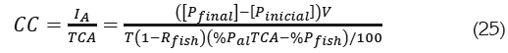
Expresión que es igual a la obtenida utilizando el modelo de Beveridge (1986) (9).
Simulación numérica: Para la simulación del modelo, se diseñó una interfaz gráfica, utilizando el software de Mathematica 7.0® (Figura 1). El modelo fue aplicado a dos cuerpos de agua con piscicultura intensiva: el Embalse Menzelet y el Lago Kesikköprü, cuya capacidad de carga fue estimada previamente por Buyukcapar & Alp (2006) y Pulatsü (2003), aplicando el modelo de Beveridge (1986). Los parámetros empleados fueron calculados con los datos proporcionados por los artículos de referencia (Pulatsü 2003; Buyukcapar & Alp, 2006) y utilizando las suposiciones de la sección anterior para asegurar un valor de equilibrio de [P] igual al máximo permitido, empleado por los autores: [Pfinal] = 60mg/m3.

En la figura 2, se muestran los resultados de Bm y [P] en función del tiempo. Se observa un crecimiento lineal de la biomasa Bm, que se explica, debido a que se supone IA constante. Cabe recordar que no se tiene en cuenta mortalidad y, por este motivo, siempre habrá crecimiento. También, se observa un aumento en la concentración de fósforo desde un valor inicial [Pinicial] hasta el valor de equilibrio [Pfinal]. El crecimiento, se explica, debido a que se está modelando la situación de inicio de piscicultura y hay ingreso de fósforo, tanto por el alimento suministrado como por otras fuentes.
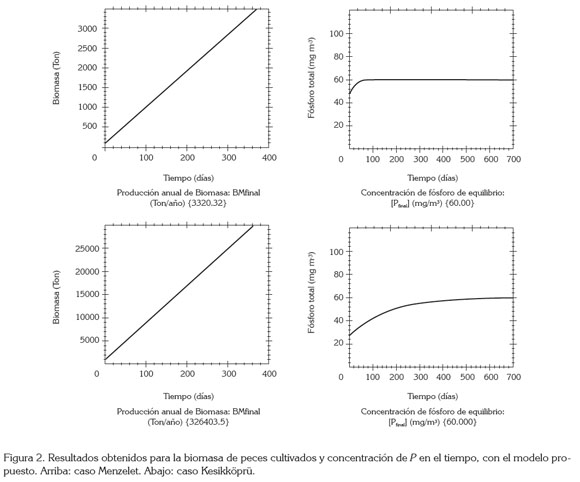
La capacidad de carga del embalse Menzelet, según el modelo de Beveridge-Dillon & Rigler fue de 25.394 ton/año, con el nuevo modelo se obtuvo un valor de 26.403 ton/año (Figura 2). Para el Lago Kesikköprü, la capacidad de carga según el modelo de Dillon & Rigler (1974) fue de 3.335ton/año y con el nuevo modelo fue de 3.320ton/año (Figura 2). La diferencia se puede explicar por las pequeñas variaciones en los valores de los parámetros utilizados en ambos modelos.
Por otro lado, el modelo permite estimar la tasa de ingreso de fósforo excedente fexc, producto de la actividad piscícola. Para el caso Menzelet, el valor es fexc = 0,8736 ton/día, lo cual, indica que la contribución al fósforo, debido a la actividad piscícola, es mayor que la registrada a la entrada por otras fuentes (fotros=0,7983 ton/día). Esto es posible, porque [Pi] = 29,0 mg/m3 es mucho menor que el valor final permitido [Pf] = 60,0 mg/m3, lo que permite una alta tasa de alimentación antes de que el sistema alcance este valor máximo de fósforo. Esto explica también el valor alto de la capacidad de carga para este cuerpo de agua: CC= 26403ton/año. Para el caso Kesikköprü, el valor es fexc = 0,1041 ton/día y fotros = 0,8003 ton/día. Esta menor entrada de fósforo excedente se puede explicar, porque antes de la actividad piscícola [Pinicial] = 53,1 mg/m3, un valor muy cercano al máximo permitido, luego la tasa de alimentación tiene que ser baja para no sobrepasar el límite de [Pf] = 60,0 mg/m3 y, como consecuencia, CC=3320ton/año es menor que el primer caso.
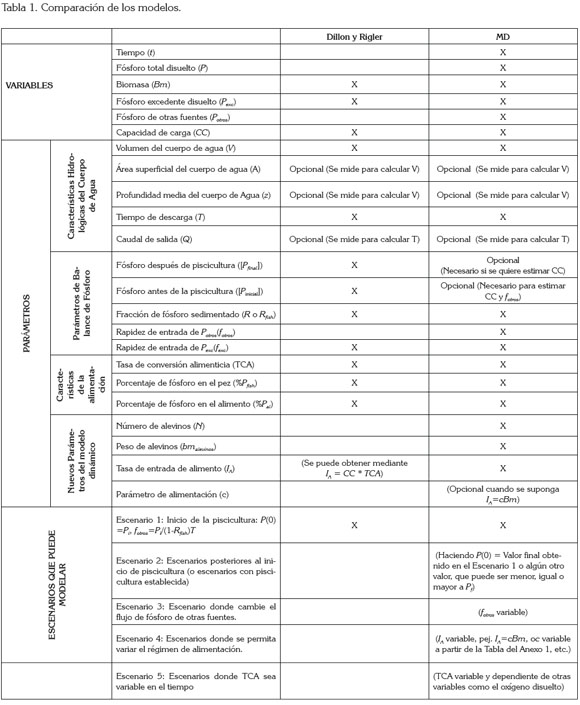
Los resultados obtenidos muestran que el modelo MD estima los mismos valores de capacidad de carga que los dados por Dillon & Rigler (1974); la ventaja del nuevo modelo es que permite conocer la dinámica de la biomasa durante el tiempo de cosecha y adicionalmente establecer mediante, el simulador, los parámetros y las condiciones iniciales, con los cuales, se obtiene la mayor producción, sin afectar el ecosistema. Por ejemplo, es posible determinar el factor IA suficiente para aumentar la biomasa de forma sostenible, con ganancias para el piscicultor y sin degradar el ambiente. También es posible estimar la entrada de fósforo, debido a otras fuentes fotros distintas a la piscicultura y determinar su grado de influencia en el nivel de fósforo presente en el cuerpo de agua. Por ejemplo, si la entrada de fósforo es muy alta no es posible aumentar lo suficiente el factor IA para obtener una mejor producción de biomasa. El modelo permite, además, simular otros escenarios, como con IA no constante, TCA variable, de acuerdo con la edad del pez o escenarios posteriores al inicio de la actividad piscícola. Es posible, del mismo modo, estimar el tiempo que debe transcurrir sin actividad piscícola para que la concentración vuelva a su estado natural. La tabla 1 compara los modelos de Dillon & Rigler (1974) y el modelo propuesto y demuestra la versatilidad y utilidad de éste: permite modelar todo tipo de situaciones derivadas de actividades acuícolas o de piscicultura intensiva, sin necesidad de medir más parámetros que los necesarios para el modelo original de Beveridge. Con el modelo y la validación presentada, la siguiente fase de este proyecto tendrá como objetivo estimar la capacidad de carga de embalses colombianos como Betania y Prado.
Conflicto de intereses: Los autores del presente trabajo declaramos que no existe ningún conflicto de intereses que ponga en riesgo la validez de los resultados obtenidos. Financiación: El proyecto fue financiado por la Universidad Jorge Tadeo Lozano.
BIBLIOGRAFÍA
1. BEVERIDGE, M. 1986. Piscicultura en jaulas y corrales. Modelos para calcular la capacidad de carga y las repercusiones en el ambiente. FAO documento técnico de pesca. Disponible desde Internet en: http:// www.fao.org/DOCREP/005/AD021S/AD021S00. HTM (con acceso 11/06/10). [ Links ]
2. BLACK, K.D. 2001. Environmental impacts of aquaculture. CRC Press, Boca Ratón (USA). 214p. [ Links ]
3. BOTTOM, D.L. 1997. To Till the water: a history of ideas in fisheries conservation. En: Stouder, D.J.; Bisson, P.A.; Naiman, R.J. eds.Pacific Salmon and Their Ecosystems: Status and Future Options. Ed. Chapman Hall (New York). p.569-597. [ Links ]
4. BRIGOLIN, D.; PASTRES, R.; NICKELL, T.D.; CROMEY, C.J.; AGUILERA, D.R.; REGNIER, P. 2009. Modelling the impact of aquaculture on early diagenetic processes in sea loch sediments. Marine Ecol. Progress Series. 388:63-80. [ Links ]
5. BUYUKCAPAR, H.M.; ALP, A. 2006. The carrying capacity and suitability of the menzelet reservoir (Kahramanmaras- Turkey) for trout culture in terms of water quality. J. Appl. Sci. 6:2774-2778. [ Links ]
6. CANOSA, A.; LÓPEZ, L.; MORALES, D.; MARTÍNEZ, P. 2008. Línea Base Microbiológica para Ajuste del POPA (Plan de Ordenamiento Pesquero y acuícola) del Embalse de Betania. Informe Técnico. Instituto Colombiano de Desarrollo Rural Integral (Colombia). Disponible desde internet en: http://www.huila.gov. co/documentos/P/POPABetaniaTexto.pdf (con acceso 10/04/10). [ Links ]
7. CROMEY, C.J.; NICKELL, K.; BLACK, D. 2002. DEPOMOD. Modelling the deposition and biological effects of waste solids from marine cage farms. Aquaculture. 214:211-239. [ Links ]
8. DILLON, P.J.; RIGLER, F.H. 1974. A test of simple budget model predicting the phosphorus concentration in lake water. J. Fish. Res. Board Can. 31:1771-1778. [ Links ]
9. DILLON, P.J.; EVANS, H.E. 1993. A comparison of phosphorus retention in lakes determined from mass balance and sediment core calculations. Water Res. 27(4):659-668. [ Links ]
10. FINDLAY, R.H.; WATLING, L. 1997. Prediction of benthic impact for salmon net-pens based on the balance of benthic oxygen supply and demand. Marine Ecol. Progress Series. 155:147-157. [ Links ]
11. LARSEN, D.P.; MERCIER, Y.H.T. 1976. Phosphorus retention capacity of lakes. J. Fish. Res. Board Can. 33(8):1742-1750. [ Links ]
12. MAGILL, S.H.; THETMEYER, H.; CROMEY, C.J. 2006. Settling velocity of feacal pellets of gilthead sea bream (Sparusaurata L.) and sea bass (Dicentrarchus labrax) and sensitivity analysis using measured data in deposition model. Aquaculture. 251:295- 305. [ Links ]
13. MILLENIUM ECOSYSTEM ASSESSMENT. 2005. Ecosystems and human well-being: synthesis. Island Press, Washington, D. C. Disponible desde Internet en: http://www.millenniumassessment.org/ documents/document.356.aspx.pdf (con acceso 15/07/10). [ Links ]
14. MORALES, V.V.; MORALES, R. 2005. Síntesis regional del desarrollo de la Acuicultura 1. América Latina y el Caribe. FAO Circular de Pesca No 1017/1. [ Links ]
15. PULATSÜ, S. 2003. The application of a phosphorus budget model estimating the carrying capacity of Kesikk. pr. Dam Lake. Turk. J. Vet. Anim. Sci. 27:1127- 1130. [ Links ]
16. SCHINDLER, D.W. 1971. A hypothesis to explain differences and similarities among lakes in the experimental lakes area, northwestern Ontario. J. Fish. Res. Board Can. 28(2):295-301. [ Links ]
17. SCHINDLER, D.W.; FEE, E.J. 1974. Experimental lakes area: whole-lake experiments in eutrophication. J. Fish. Res. Board Can. 31(5):937-953. [ Links ]
18. STICKNEY, R.R. 2003. How did we get into this mess? Junk science vs. real science. World Aquaculture. 34:71. [ Links ]
19. STIGEBRANDT, A.; AURE, J.; ERVIK, A.; HANSEN, P.K. 2004. Regulating the local environmental impact of intensive marine fish farming III. A model for estimation of the holding capacity in the Modelling-Ongrowing fish farm-Monitoring system. Aquaculture. 234:239-261. [ Links ]
20. SONZOGNI, W.C.; CHAPRA, S.C.; ARMSTRONG, D.E.; LOGAN, T.J. 1982. Bioavailability of phosphorus inputs to lakes. J. Environ. Qual. 11:555-562 [ Links ]
21. VALLENTYNE, J.R. 1974. The algal bowl lakes and man. Dep. Environ. Fish. Mar. Serv., Ottawa. Misc. Publ. 22. 186p. [ Links ]
22. VOLLENWEIDER, R.A. 1968. The scientific basis of lake and stream eutrophication with particular reference to phosphorus and nitrogen as eutrophication factors .Tech. Rep. OECD, Paris, DAS/CSI 68. 27:1-182. [ Links ]
Recibido: Agosto 25 de 2011 Aceptado: Abril 10 de 2012













