Comparación de la solución analítica de la función de producción de COBB-DOUGLAS con la obtenida por el método de mínimos cuadrado

Comparison of the analytical solution of the COBB-DOUGLAS production function with obtained by the method of least squares

¹Matemático. Docente de la Universidad Distrital Francisco José de Caldas. Bogotá, Colombia. wadiazo@udistrital.edu.co
²Tecnólogo en Electricidad. Estudiante de Ingeniería Eléctrica de la Universidad Distrital Francisco José de Caldas. Bogotá, Colombia, diego.a.giral@gmail.com

Fecha de recepción: mayo 14 de 2010 Fecha de aceptación: noviembre 23 de 2010.

Resumen

En el presente artículo se hace un detallado análisis descriptivo mático de la función de producción de Cobb-Douglas, y se compara la solución analítica con la obtenida con la utilización del método de mínimos cuadrados. De igual manera, se realiza un breve recuento histórico de su origen y se da una hipótesis sobre cómo Charles Cobb y Paul Douglas llegaron a la formulación algebraica de la función de producción que describe el crecimiento de la economía estadounidense en el período comprendido entre 1899 a 1922.

Palabras clave: Función de producción, capital, ingresos, Mínimos cuadrados, Solución numérica.

Abstract

In this article a detailed descriptive analysis mathematica lfunction Cobb-Douglas production, and compared with analytical solution obtained using the least squares method. Also there is a brief history of its origin, and explains a possible way as Charles Cobband Paul Douglas came to the algebraic formulation of the production function that describes the growth of the U.S. economy in the period from 1899 to 1922.

Key words: Production function, Least squares, Numerical solution.

1. Introducción

Este artículo hace referencia a la función de producción de Cobb-Douglas, la cual fue publicada en 1928 por Charles Cobb y Paul Douglas, quienes realizaron un estudio en el que se modeló el crecimiento de la economía estadounidense durante el período de 1899 a 1922.

Para analizar esta función de producción se realizará una breve reseña de su origen y se explicará, detalladamente, una posible forma de cómo Charles Cobb y Paul Douglas llegaron a la formulación algebraica de la función de producción que describe el crecimiento de la economía estadounidense en el período anteriormente mencionado. Por último, se comparará la solución exacta de la ecuación diferencial con la obtenida por el método de mínimos cuadrados.

2. Estado del arte

A través de la historia la fluidez de las ideas económicas han partido de la búsqueda de organizar los diferentes factores que influyen en el crecimiento de una nación. Los modelos e ideas económicos planteados han constituido un proceso en constante cambio que se ha caracterizado por la intervención de múltiples personajes¹.

3. Función de producción de Cobb-Douglas

Antes de realizar el análisis descriptivo mático de la función de producción de Cobb-Douglas, es necesario describir cada uno de los factores involucrados en el modelo.

3.1. Función de producción

Una función de producción es la relación entre las cantidades máximas de productos que una empresa puede fabricar mediante el uso de diversas cantidades de insumos. [2] Las múltiples funciones de producción que actualmente se manejan están representadas por la combinación de factores de insumo (la tecnología disponible por industria refleja la cantidad de factores implementados) [3].

Una función de producción se expresa como la Ecuación 1 [4][5].

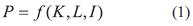
P: cantidad de producción

K, L, I: Representan los factores de insumo, cada una de estas letras determina una característica especial del insumo.

Existen diversas maneras de expresar la función de producción (Ecuación 1), la primera consiste en una representación lineal o aditiva (Ecuación 2) [4] [6].

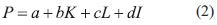
Donde a, b, c, dson parámetros que se determinan empíricamente [4] [6].

Otra representación (Ecuación 3) está dada por la función de producción de Cobb-Douglas.

b: Productividad Total de los Factores (PTF) es una constante independiente tanto de L como de K, la variación de la PTF es el ritmo al que se producen los cambios tecnológicos, organizacionales y en la gestión de las empresas, y trata cualquier efecto en salida total no causado por las entradas o las economías a escala [7][8][9].

α y β: son constantes entre cero y uno que miden la participación del capital en la renta, a determina la proporción de la renta que obtiene el capital y la que obtiene el trabajo, β es igual a la unidad menos a [10].

Además, las constantes a y β tienen un significado económico de acuerdo a su valor.

α + β = 1: la función de producción tiene vueltas a escala constantes (cambios en la salida subsecuente a un cambio proporcional en las entradas) [11].

α + β < 1: la función de producción tiene vueltas a escala que disminuyen [11].

α + P > 1: la función de producción tiene vueltas a escala que aumentan [11].

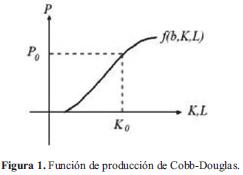
3.2. Curva de la función de producción de Cobb-Douglas

Las funciones de producción se pueden representar gráficamente como se muestra en la Figura 1. Todos los puntos por encima de la función de producción son imposibles de obtener con la tecnología actual; todos los puntos representados a continuación son técnicamente factibles [4].

3.3. Deducción algebraica de la función de producción de Cobb-Douglas

Dentro de las suposiciones básicas de la función de producción de Cobb-Douglas, se tiene:

• Si la mano de obra o capital se reduce, la producción también se reduce en la misma producción.

• La productividad marginal de la mano de obra es proporcional a la cantidad de producción por unidad de mano de obra.

• La productividad marginal del capital es proporcional a la cantidad de producción por unidad de capital.

Con base a dichas suposiciones, se plantean las ecuaciones diferenciales relacionadas con este comportamiento:

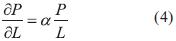
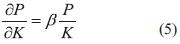
En relación a las ecuaciones (4) y (5) se puede decir que:

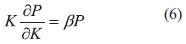
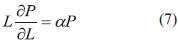
Sumando las ecuaciones (6) y (7), sería

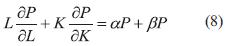
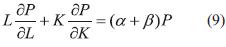
Haciendo r= a + b, entonces

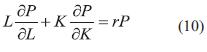
La ecuación (8) es equivalente al teorema de Euler para funciones homogéneas, lo que indica que si r= 1 entonces se tendrá una ecuación homogénea de grado 1 y:

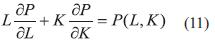
En la sección 3.5 resolvemos analíticamente esta ecuación.

La ecuación (4) proporciona la productividad marginal de la mano de obra. Como esta ecuación es una ecuación diferencial ordinaria, la solución la hallamos separando variables e integrando. Así , obtenemos:

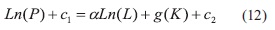
O equivalente,

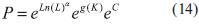
Haciendo A = e^c y h(K) = e^g(k) la Ecuación. (14) se transforma:

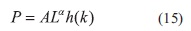
Basta con hallar la función h (k). Se sabe que:

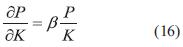
Derivando parcialmente la función encontrada en el procedimiento anterior y reemplazando:

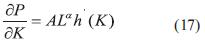
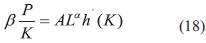
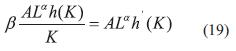
La cual se convierte en una ecuación diferencial ordinaria:

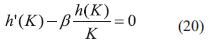
La solución de esta ecuación diferencial es h(k) = K^β. Lo cual se verifica fácilmente, ya que al reemplazar en la ecuación anterior se obtiene una identidad. Luego,

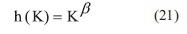
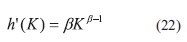
Reemplazando en la Ecuación (20):

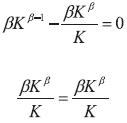
Realizando la sustitución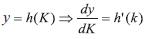

Reemplazando en la Ecuación (20)

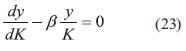
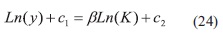
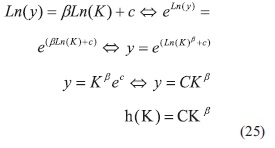
Luego de encontrar h(k), tenemos que

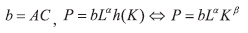
Y dentro de la suposición de la función de producción se sabe α + β = 1, por lo tanto

3.4. Regresión lineal de la función de Cobb-Douglas para un caso en particular

Para poder hallar los valores de α y β y b se debe linealizar la función de producción.

La Ecuación (26) la podemos escribir como 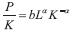de donde

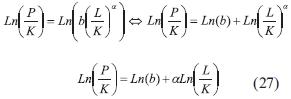
Para citar un ejemplo de la función de producción, se toman como referencia los datos publicados por el Gobierno americano desde al año 1899 hasta 1922, citados en [9]. P es la producción total, L cantidad de mano de obra y K la cantidad de capital invertido, adicionalmente se incorporan dos columnas que permiten realizar la Idealización de la función.

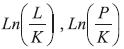
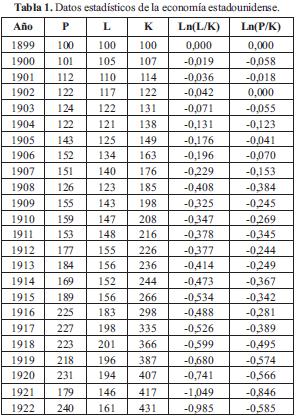
Con los datos de la Tabla 1, utilizamos el método de mínimos cuadrados para encontrar una tendencia lineal:

La pendiente de la recta se obtiene mediante

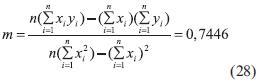
Y el intercepto mediante

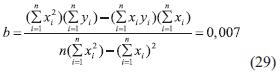
Luego, la ecuación de la recta que mejor se ajusta a los datos es

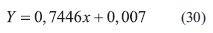
Como se muestra en la Figura 2.

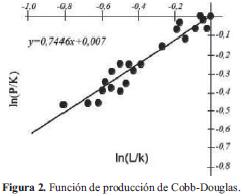
Se realiza una comparación entre las Ecuación (29) y (32)

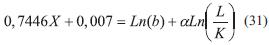
Donde, α = 0,745, Ln(b) = 0,007, e ^Ln(b)= e^0,007, b = e^0.007 b = 1,00702

Aproximando los valores: α = 0,75, b = 1,01

Por lo tanto, la función de producción de Cobb-Douglas para los datos de la Tabla 2 es:

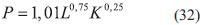
3.5. Solución analítica de la ecuación diferencial

Ahora resolvemos analíticamente la Ecuación (11), utilizando el método de las características [12]. Las ecuaciones características son

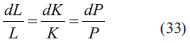
Este sistema de ecuaciones nos lleva a las curvas solución:

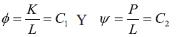
Donde C₁ y C₂ son constantes arbitrarias. Por lo tanto, la solución general de (11) es

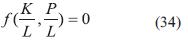
Donde ƒ es una función arbitraria. Esta solución también la podemos escribir como

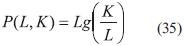
Donde g es una función arbitraria. Comprobemos que, si por ejemplo, 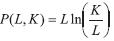. es solución de la Ecuación (11) (tomamos g como la función logaritmo natural).

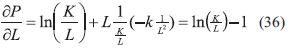
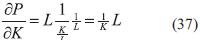
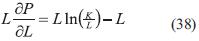
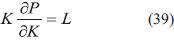
Sumando (38) y (39):

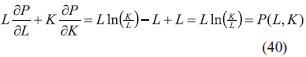
Observamos que si g es la función logaritmo natural, en este caso, también podemos escribir una solución de (11) como:

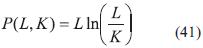
Esto nos permite concluir que, a pesar de que hay infinitas funciones solución de la Ecuación (11), la mejor aproximación de la función de producción de Cobb-Duglas es precisamente la que se obtiene por medio del método de mínimos cuadrados (linealización de los datos).

4. Conclusiones

El desarrollo histórico de la economía tuvo su aporte más importante en los modelos násicos; aunque en la economía moderna la interpretación clásica es aún una herramienta de trabajo, la imple-mentación de las matemáticas permitió a la economía la vinculación en nuevos campos y alejarse un poco de su historia ética.

Las funciones homogéneas, las derivadas parciales y las ecuaciones diferenciales, ordinarias y parciales, juegan un papel fundamental en la economía, cuya utilidad fue orientada en este caso en la predicción de la economía estadounidense hacia modelos de producción. Las derivadas parciales fueron el inicio de las hipótesis formuladas por Cobb y Douglas, ya que éstas describí an a la perfección las razones de cambio de las cuales depende la economía a nivel general, esto indica que en una función de producción se tienen en cuenta los múltiples factores que intervienen en los modelos económicos. En este caso, en la función de producción de Cobb-Douglas se manejan dos variables importantes: capital y mano de obra.

Se determinó de manera sencilla y algebraicamente la forma de la función de producción de Cobb-Douglas. La linealización obtenida a partir de los datos de la Tabla 2 es la mejor aproximación a la solución de la función de producción de Cobb-Douglas.

Pie de página

Para la escuela clásica y durante posteriores décadas, la economía no se asumió como una ciencia sino como una disciplina intelectual, fue caracterizada como un modelo ético, contaminado por los valores estéticos, morales, religiosos, políticos o ideológicos. Es importante resaltar que uno de los primeros pensadores económicos que aún influencia los modelos de economía moderna es Aristóteles, su aporte consistió en vincular la economía con la satisfacción de necesidades para conseguir un determinado fin [1].

Referencias bibliográficas

[1] R. Domínguez. La economía como ciencia social: evolución de su objeto y método. [En línea]. Disponible en: http://personales.unican.es/domingur/Intro.pdf.        [ Links ]

[2] I. B. Tucker. Fundamentos de Economía, México: Thomson Learning, 2002.        [ Links ]

[3] J. D. Castrillón, La función de producción, Universidad de Tulane. New Orleans. [En línea]. Disponible en: http://www.elprisma.com/apuntes/economia/lafuncionproduccion/.        [ Links ]

[4] WordIQ. Production function. [En línea]. Disponible en: http://www.wordiq.com/definition.        [ Links ]

[5] F. Mochón, V. Becker, Resumen del libro - Elementos de Micro y Macroeconomía. España: McGrawHill, 1994.        [ Links ]

[6] WorldLingo. Función de producción. [En línea]. Disponible en: http://www.worldlingo.com/ma/enwiki/es/Production_function.        [ Links ]

[7] Diccionario Economía - Administración -Finanzas - Marketing, Productividad total de los factores. [En línea]. Disponible en: http://www.eco-finanzas.com/diccionario/P/PRODUCTIVIDAD_TOTAL_DE_LOS_FACTORES.htm.        [ Links ]

[8] WorldLingo. Productividad total del factor. [En línea]. Disponible en: http://www.worldlingo.com/ma/enwiki/es/Total_factor_productivity.        [ Links ]

[9] J. Stewart, Cálculo: trascendentes tempranas, Sexta Edición. México: Cengage Learning, 2008.        [ Links ]

[10] N. G. Mankiw. "Macroeconomía", La economía a largo plazo, Cuarta Edición, Capítulo 2, p. 92, España, 2000.        [ Links ]

[11] C.Charles and P. Douglas (1928). Cobb-Douglas. 2009. [En línea]. Disponible en: http://www.worldlingo.com/ma/enwiki/es/Cobb-Douglas.        [ Links ]

[12] P. O'Neil, Beginning partial differential equations. New York: John Wiley Sons, 1999.        [ Links ]