Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Tecnura
Print version ISSN 0123-921X
Tecnura vol.16 no.32 Bogotá Apr./June 2012
KANBAN allocation in a serial suply chain
Asignación KANBAN en una cadena serial de suminsitros
Guillermo Andrés Sánchez C1, Juan Manuel Sanchez C2, Oscar Huberto Patiño H3
1 Ingeniero Electrónico, Magister en Ingeniería Electrónica. Investigador de la Universidad de los Andes. Bogotá, Colombia. guille_andre@hotmail.com
2 Ingeniero Electrónico, Especialista en Teleinformática, Magister en Administración y Negocios. Docente e investigador de la Universidad Manuela Beltrán. Bogotá, Colombia. jmsanchezcespedes@gmail.com
3 Ingeniero Mecánico, Magister en Manufacturing Engineering and Management. Investigador de la Universidad de Nottingham. Nottingham, Inglaterra. oscarpat1@gmail.com
Fecha de recepción: Agosto 24 de 2011 Fecha de aceptación: Febrero 27 de 2012
Abstract
The aim of this project is to simulate a Kanban system using N stages with the objective of maintaining an acceptable throughput and mean system time. The document shows the production systems where Kanban is applicable and what the potential benefits are. A serial of simulations will be done using a demand given by a poison distribution with rate λ ∧ ext. The simulation aimed to find the best number of withdrawal Kanban on all N stages when the values of µ (for exponential distribution of the process) and λ ∧ ext increase and decrease. At the end of this simulation, the best way to allocate the withdrawal Kanban over N stages with the objective of maintaining acceptable throughput and mean system time will be clearer thus the conclusions of this work will be done.
Key words: discrete systems, Just In Time, KANBAN, Lean production, Queue systems.
Resumen
El objetivo de este proyecto es simular un sistema Kanban usando N etapas con el objetivo de mantener un aceptable rendimiento y tiempo medio del sistema. El documento muestra los sistemas de producción donde Kanban es aplicable así como sus potenciales beneficios. Se realizó una serie de simulaciones usando la demanda dada por una distribución de Poisson con tasa λ. El objetivo de la simulación fue encontrar el mejor numero de ingenio Kaban en todas las N etapas de donde los valores (para una distribución exponencial del proceso) y λ se incrementan y decrementan. Al final de la simulación se determina la mejor manera de asignar las cadenas Kanban sobre los Nescenarios con el objetivo de mantener un buen rendimiento y tiempo medio del sistema.
Palabras clave: sistemas discretos, justo a tiempo, KANBAN, producción Lean, sistema de colas.
1. Introduction
Production processes are in general complex systems that require robust administration systems for its control. New production theories like TPS and Lean Manufacturing has been imported from Japan and implemented in the last two decades in the western world. One of the tools used under these production systems is the kanban systems.
These systems help not only to reduce the amount of time on the administration of production (production order generation and administration, administration of inventories, control of production itself) but also to reduce and maintain low inventory levels and good service levels in terms of satisfying the customer demand.
The simulation of the kanban system will help to understand the necessary elements inside the system and also to determine the effect on the output by the variation of the conditions inside the system and the variation of the system by the variation of the demand.
This document gives a briefidea of the traditional production systems, the aim of lean manufacturing and the impact of use of Kanban. Then, it is described the approach to implement a queuing system to simulate kanban and the different variables to be used on its simulation.
2. Production systems
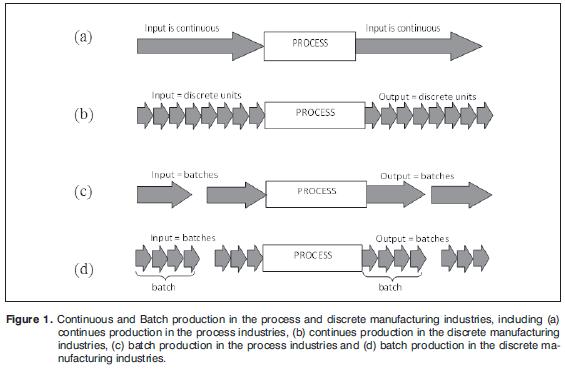
The production systems can be classified according the continuity in the manufacture of the product, the two kinds of systems are Continues production and Batch production, see Fig. 1 [1].
The Continuous production is characterized by the use exclusive of the production equipment to a given product, no interruptions in the output of the manufacture of product and without breaks for product changeovers. The Batch production is characterized by process a finite amount of products, the production is made in a discontinued way by many reasons: because the necessity of a setup to produce different models of a same product to supply the demand; because the manufacturing process can only be done in batch for nature of process and machines (e.g. furnace ovens, chemical reactors, chemical or physical treatments).
3. Production facilities
An important aim for a manufacturing company is to organize its facilities in the most efficient way. To do this, it is important to consider the type of product, the variety in the type of product and quantity of products that are made by the factory. The last two factors are inversely correlated but these help to show an appropriate organization of the facilities according to each case [1].
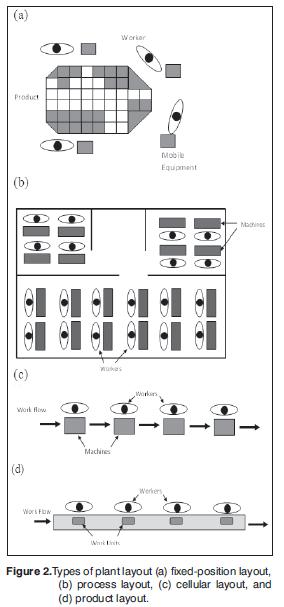
For a factory with low volume production (it means quantity production in the range of 1 to 100 units per year) the associated production facility is the job shop type, which generally implies customized products and high complexity. The kind of products associated, are so specialized and different each one to another that is necessary have a very flexible job shop. In some cases the product is very large or very heavy, then to move the equipment around the product is the easiest way to do it, this kind of layout is called f xed- position layout.
For the fabrication of smaller components of a bigger product it is necessary a product layout, where the fabrication sequence of each part can be changed easily according the customized product, these parts generally are done by batches.
For a factory with medium volume production (it means quantity production in the range of 100 to 10.000 units per year), there are two different situations: high product variety and low product variety. If the case is the company has high product variety, the production is normally made by batches and frequently organized in a production layout. Usually between each batch production it is necessary a setup time. During this time the facility changes the required dies and tools and the equipment is reprogrammed for the new product. This setup time by definition is a kind of down-time (there are other down-times associated to workers and stoppages due to machine break-downs). Traditionally, to avoid disruption in the process due to the required time for changeover, batch production works with calculated intermediate stocks to avoid the changeover interference. Currently the tendency is to reduce the changeover time and by consequence reduce the intermediate stocks (if not eliminate them).
In the other hand, if the medium production factory works with low variety products it is possible to work with a cellular layout. Each cell is responsible to do a set of similar parts, having several workstations but minimum changeovers given the low variety of the products.
For a factory with high volume production (it means quantity production higher than 10.000 units per year) is related to the mass production, and it is classified in quantity production and flow line production.
The Quantity production works to do single parts on single pieces of equipment and it is usually implemented with process layout. The Flow line production works with multiple workstation organized in sequence, in this way the part or product moves in that sequence until be completed. In this type of production can be used a product layout generally connected by a conveyor, or into a series of connected line segments. The most representative example is an assembly line of cars, in this case the production can work as a single model production line or as mixed model production line with low variety in the making of each car customized.
Clearly the process layout, cellular layout, and production layout are managing different amounts of products, but they have the common issue which is the administration of stocks; produce efficiently at low cost and to generate benefits per each produced part. An administration system that last two decades has growth in acceptance and has shown good benefts in terms of savings and increased efficiency is the Lean Manufacturing or more generally the Lean Thinking.
4. Lean thinking
Lean Thinking tries to answer two basic questions: ¿How do people inside organizations can make mass production organizations make them lean? and ¿What are the key principles to guide our actions? [2].
Five main concepts could answer these questions and summarize the Lean Thinking concept:
-
Value: Defined from the point of view of the customer and not from inside the supplier. In other words defne what is valuable for the customer and what is not.
-
Value Stream: Defne the sequence of steps from raw material to the customer. It could be defned for the enterprise or its supply chain.
-
Flow: Make the value fow. Keep moving the value and avoid batches and queue, or at least reduce it. But always it is necessary to remember the objective: fow one by one.
-
Pull: Only produce when it is needed and have a short-term response to the customer. At the macro level being prepared for fluctuations in demand, and at micro level maintaining the fow operative at the rhythm of the demand.
-
Perfection: It does not mean only defect free, it means also delivering exactly what the customer wants, when they wants and at a fair cost with minimum waste [2].
Lean production ideology is mainly based in the Just In Time (JIT) production system. This System was developed by Toyota Motor Corporation and its main goal is " to enable production of a variety of end items in a timely and efficient manner, smoothly synchronized with the production and delivery of component materials and without reliance on the conventional stratagem of keeping extra work-in-process and finished goods inventory"[3], it can be summarized in a simple way as: "The just-in-time concept entails producing the necessary units, in the necessary quantities, at the necessary times"[3]. One of the most useful tools to implement this approach and to control production eff ciency and inventory level (helping to the fve Lean Thinking principles) is the Kanban-System which is introduced below.
5. Kanban System
Kanban is a Japanese word that means card o ticket.
The kanbans cards circulate always with the material fow and for each card, there is a container carrying a previously agreed number and type of part.
The typical information on kanban cards is [4]:
- Part number and name.
- Process name where is been used.
- Number of units in the container.
- Number of kanban cards issued.
- Preceding process outbound stock point number and subsequent process inbound stock point number.
The kanban system must work in a leveled production schedule, it means that the main fluctuation of the demand has been smoothed, and the kanban system self-regulates to maintain the needed production quantities while absorbing the minor variations in every operation.
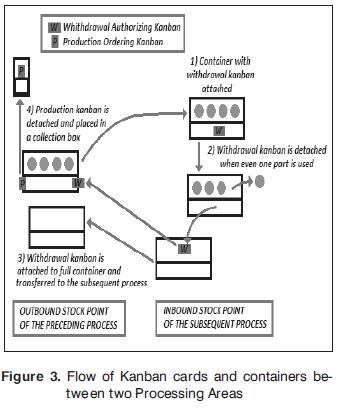
The circulation of the kanban cards through the manufacturing system is the way that the flow of material and production is controlled. The kanban cards used to control the fow of material are called withdrawal authorizing kanbans, and the kanban cards used to control the production are called production-ordering kanbans.
The Fig. 3[4] shows the circulation of these kanbans cards in a simple example of a manufacturing process between two processing areas.
The rules of this kanban system are:
Every container at inbound stock must have a withdrawal kanban attached
-
When the frst unit of a container in inbound stock is used for the subsequent process, the withdrawal kanban is detached, and then it is attached to an empty container and placed in the outbound stock point of preceding process.
-
When the preceding process has a full container in the outbound stock point, its production kanban is detached and placed in a collection box, meanwhile a withdrawal kanban is attached, and finally the full container is transferred to the inbound stock point of the subsequent process.
-
The production kanban cards are collected from the collection box, and these authorize the production of more full containers. When these are produced the production kanban cards are attached to each container.
The dynamic of this kanban system can be extended for a manufacturing process with n stages. Always the production of parts on stage i begin with the withdrawal kanban given from stage i+1, in this way the serial supply chain works from stage n-1 until stage 1 supplying the parts of the next stage, and thus the stage n supply the demand of product ended.
6. Model of kanban system for a serial supply chain
6.1 Single Stage
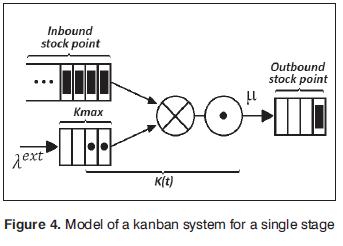
The simplest way to start the design of a model for the kanban system is creating the model of a single stage as a queue system. The model of this queue system has the next characteristics[5]:
- Has unlimited input material
- Exponential distributed container processing times with rate µ.
- Poisson demand arrivals with rate λ ∧ext.
- No backorders.
The estate of the system is given by the number of active kanbans at that moment, where the number of active kanbans is equal to the total number of kanbans minus the number of full containers. The Fig. 4 shows the model of a kanban system for a single state.
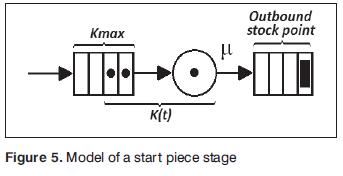
Where K(t) is defned as the number of active kanbans in time t, and Kmax is the number of availed kanbans for the single station. The value of K(t) increases when a full container is removed from the outbound stock point and its withdrawal kanban is detached and it change to be an active kanban. The value of K(t) decreases when a container is flled and a active kanban is attached to it, and then the full container is placed in the outbound stock point.
6.2 Start piece stage
From the model of a single stage is easy to develop the model for the start piece stage in a kanban system. The change that must be done is to simplify the input stock queue with the withdrawal kanban queue, this simplifcation results in the withdrawal kanban queue because this always will be the shortest queue and thus it defines the dynamic of the start piece stage. The Fig. 5 shows the model for a start piece stage, and K(t) increase and decrees in the same way that a single stage. In this case the demand cannot be determined in the same stage; it is done in the next one.
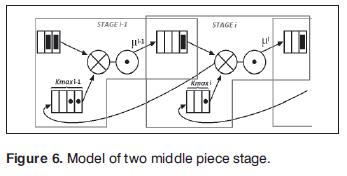
6.3 Middle piece stage
A middle piece stage model use the same model for a single stage but with two differences that help to connect it with the preceding stage and the subsequent stage:
- When the stage i starts using a full container, a withdrawal kanban is returned to stage i-1.
- The outbound stock point of stage i-1 is the same inbound stock point of stage i.
- The maximum possible number of full containers in the stage i is equal to the maximum number of withdrawal kanbans that handle the stage i-1.
The Fig. 6 shows the model of two middle piece stage, each stage has their own exponential distributed container processing time, and their maximum number of withdrawal kanbans.
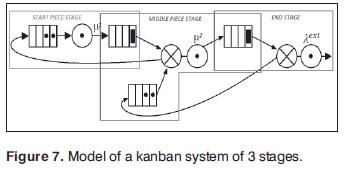
6.4 End stage
This stage is not a manufacturing stage, this stage represent the store, where the inbound stock point has the number of ended products. In this case neither the kanban queue nor the outbound stock point are necessary, because the next destination of production is out of the system, it also indicates that the demand is given by a Poisson distribution with rate λext.
Fig. 7 shows the model of a kanban system with start piece stage, middle piece stage and end stage.
For the making of a model of a kanban system in a serial supply chain of N stages is needed the next:
- 1 star piece stage, and define 1 rate I for exponential distribution of the container processing.
- N-2 middle piece stages, and define N-2 rate I for exponential distributions for the different container processing.
- 1 end stage, and define 1 rate λext for the Poisson distribution for the demand arrivals.
- Define the number of kanban cards in each stage.
7. Conclusions
As variation is always present in production process and supply chains, it is expected that simulations´ results will be close related with the variation level of the system. This means that the higher the variation of the bigger the number of kanbans. In the same way the bigger the number of kanbans the longer the time the material will be in the chain and, more uncertainty about the time it will take to be processed and delivered to the last station or customer.
It is expected that the number of kanban cards allocated for each station will be related not only to the associated variability of each station but to the previous and next stations and at the end to the whole system. In addition, it is expected that, for the system itself, it will be more useful to reduce variation at the beginning of the chain rather than the end, where process f exibility is also relevant.
8. Future Work
The aim of this project is to answer the next question: How should be allocated the withdrawal kanbans over N stages in order to maintain an adequate throughput and acceptable mean system time? To answer this question, a serial of simulations will be done with the next scenarios, always with the objective to maintain an adequate throughput and acceptable mean system time:
-
Find the best values of I and λ∧ext for each stage, when the withdrawal kanbas in all stage is equal to 1 and N=5.
-
With the result of the previous simulation, analyze the results of simulation if the number of withdrawal kanbans increase in the same way.
-
With the result of first simulation, find the best value of µ3 if that station increase the number of withdrawal kanbans.
-
With the result of previous simulation, find the best value of µ2 and µ3 if those stations increase the number of withdrawal kanbans.
-
With the result of previous simulation, find the best value of µ1 and λext if those stations increase the number of withdrawal kanbas.
-
Find the best values of µ and λ∧ext for each stage, when the withdrawal kanbas in all stage is equal to 3 and N=5.
-
With the result of previous simulation, find the best number of withdrawal kanbans on all stage when the value of µ3 increases and decrease
Referencias
[1] M. Groover, (2008). Automation, production Systems and Computer-Integrated manufacturing, USA: Pearson International, 3rd Edition, USA, 2008. [ Links ]
[2] J. Womack, D. Jones, Lean Thinking, Barcelona: Free Press Business, 2003. [ Links ]
[3] M. Yasuhiro, H. Aigbedo, Just-In-Time and Kanban Scheduling. In Maynard's Industrial Engineering Handbook, Boston:McGraw-Hill. 2011. [ Links ]
[4] T. Enkawa, S. J. Schvaneveldt, Just-in-Time, Lean Production, and Complementary Paradigms, in Handbook of Industrial Engineering: Technology and Operations Management, Hoboken: John Wiley & Sons. 2007. [ Links ]
[5] G. Krieg, (2005) Kanban-Controlled Manufacturing Systems. Berlin: Germany, springer. 2005. [ Links ]