Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista de la Academia Colombiana de Ciencias Exactas, Físicas y Naturales
Print version ISSN 0370-3908
Rev. acad. colomb. cienc. exact. fis. nat. vol.36 no.139 Bogotá Apr./June 2012
MATEMÁTICAS

* Departamento de Matemáticas, Universidad del Valle, Apartado Aéreo 25360, Cali, Colombia E-mail: alvarogr@univalle.edu.co
 Universidad Industrial de Santander. Bucaramanga, Colombia. E-mail: ateheran@gmail.com
Universidad Industrial de Santander. Bucaramanga, Colombia. E-mail: ateheran@gmail.com
AMS Classification 2000: 14G05.
Abstract
In this paper we give a generalization of two results obtained by Garcia and Stichtenoth 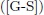 and use them to exhibit a method to construct curves over finite fields whose number of rational points is large compared to their genus. Such curves are induced by algebraic functions fields obtained from elementary abelian
and use them to exhibit a method to construct curves over finite fields whose number of rational points is large compared to their genus. Such curves are induced by algebraic functions fields obtained from elementary abelian  -extensions of the rational function field
-extensions of the rational function field 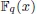 using the trace operator
using the trace operator 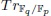
Key words: Finite Fields, Algebraic Curves, Algebraic Function Fields, Elementary Abelian  -Extensions, Rational Points.
-Extensions, Rational Points.
Resumen
En este articulo generalizamos dos resultados obtenidos por García & Stictenoth en ([G-S]) y usamos estas generalizaciones para construir curvas sobre cuerpos finitos cuyo número de puntos racionales es grande en comparación con su género. Tales curvas son obtenidas considerando  -extensiones abelianas elementales del cuerpo de funciones racionales
-extensiones abelianas elementales del cuerpo de funciones racionales 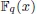 usando el operador traza
usando el operador traza 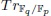 .
.
Palabras clave: Cuerpos finitos, curvas algebraicas, cuerpos algebraicos de funciones,  âextensions abelianas elementales, puntos racionales
âextensions abelianas elementales, puntos racionales
1. 1. Elementary Abelian  -Extensions
-Extensions
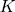 a perfect field of characteristic
a perfect field of characteristic 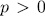 , by
, by 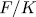 an algebraic function field with constant field
an algebraic function field with constant field 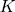 and by
and by
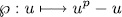
the Artin-Schreier operator.
Definition 1.1. For a subset 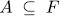 we denote by
we denote by 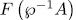 , the splitting field of all polynomials
, the splitting field of all polynomials 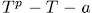 , with
, with 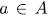 . For
. For 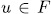 such that
such that 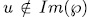 the extension
the extension 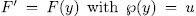 is called an Artin-schreier extension of
is called an Artin-schreier extension of  .
.
The following theorem provides a complete description of the Artin-schreier extensions. Its proof depends essentially on the following lemma.
Lemma 1.2. (Hilbert's Theorem 90) Let 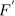 be a finite extension of
be a finite extension of  whose Galois group G is cyclic generated by
whose Galois group G is cyclic generated by 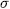 . Then
. Then 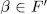 has the form
has the form 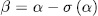 for some
for some 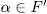 , if and only if
, if and only if 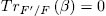 .
.
Prooƒ: see [L-N] Theorem 2.25.
Theorem 1.3. Let  be a field of characteristic
be a field of characteristic 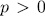 . The polynomial
. The polynomial
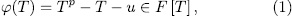
either splits completely over  or else,
or else, 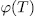 is irreducible over . Moreover the following assertions are equivalent:
is irreducible over . Moreover the following assertions are equivalent:
Prooƒ: Suppose that(1)
is a cyclic extension of degree
.
(2)
, whose minimal polynomial over
is
, where
is defined as (1), for some
.
(3)
is the splitting field of an irreducible polynomial of the form (1), for some
.
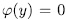 , then for
, then for 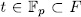 we have
we have 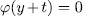 and since
and since 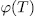 is a separable polynomial of degree
is a separable polynomial of degree  , it follows that
, it follows that 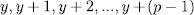 are all its roots.
are all its roots. Now, its is clear that, if 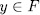 , then
, then  is the splitting field of
is the splitting field of 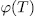 .
.
It remains to consider the case 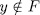 . Let
. Let 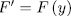 . To prove that
. To prove that 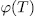 is irreducible over
is irreducible over  it is enough to prove that
it is enough to prove that 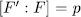 , that is to say, that
, that is to say, that 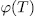 is the minimal polynomial of
is the minimal polynomial of 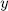 over
over  (which, from now on, we will denote by min
(which, from now on, we will denote by min 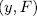 ).
).
Since 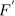 is the splitting field of the polynomial
is the splitting field of the polynomial 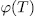 we have that
we have that 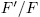 is a Galois extension, therefore, it is sufficient to show that
is a Galois extension, therefore, it is sufficient to show that 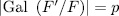 .
.
For this end, observe that since each 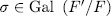 is completely determined by its action on
is completely determined by its action on 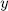 and
and 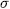 permutes all the roots of
permutes all the roots of 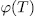 , then
, then 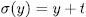 for some
for some 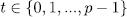 , hence,
, hence, 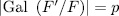 .
.
Now we will to prove the equivalences:
 suppose that
suppose that 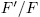 is a cyclic extension of degree
is a cyclic extension of degree  and let
and let 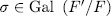 be such that
be such that 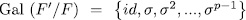 . Since
. Since 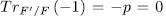 , then by Lemma 1.2, there exist
, then by Lemma 1.2, there exist 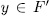 such that
such that 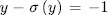 . Moreover, since
. Moreover, since 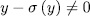 and
and 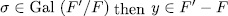 .
.
On the other hand, observe that 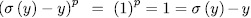 . That is to say,
. That is to say,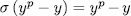 , then
, then 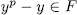 therefore, there exist
therefore, there exist 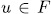 such that
such that 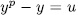 and consequently
and consequently 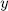 satisfies the polynomial
satisfies the polynomial 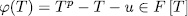 .
.
Now, since
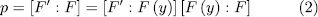
and
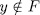 then
then 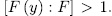 . Thus
. Thus 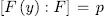 and (2) ensures that
and (2) ensures that 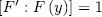 , which is the same as,
, which is the same as, 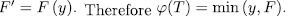 .
. 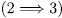 If
If 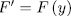 , with
, with 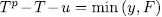 we have that
we have that 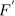 is the splitting field of min
is the splitting field of min 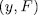 .
.
 Assume that
Assume that 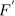 is the splitting field of an irreducible polynomial of the form
is the splitting field of an irreducible polynomial of the form 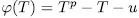 for some
for some 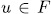 . Again by similar arguments as above we obtain that
. Again by similar arguments as above we obtain that 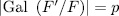 , which means that
, which means that 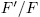 is cyclic of degree
is cyclic of degree  .
.
Definition 1.4. An extension 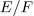 is said to be an Elementary Ableian
is said to be an Elementary Ableian  -Extension of exponent
-Extension of exponent  and degree
and degree 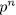 if
if 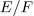 is Galois with
is Galois with 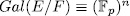
The following Theorem states a relationship between the additive subgroups of  and the elementary abelian
and the elementary abelian  -extensions. To this end, we first need to establish a result.
-extensions. To this end, we first need to establish a result.
Theorem 1.5. Let  be a field of characteristic
be a field of characteristic  >0. There exist a one to one correspondence between the additive subgroups U of
>0. There exist a one to one correspondence between the additive subgroups U of  containing
containing 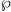 F which have finite index (U:
F which have finite index (U: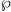 F), and the elementary abelian
F), and the elementary abelian  -extensions. This correspondence is given by
-extensions. This correspondence is given by
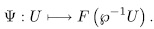
In such case
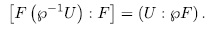
The inverse map of 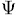 is given by
is given by
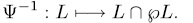
Prooƒ: see {16} page 263
Remark 1.6. observe that, regarding abelian P-torsion group as vector spaces over 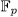 we can as well define
we can as well define 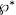 as the map (induced by
as the map (induced by 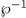 ) that takes finite-dimensional vector subspaces
) that takes finite-dimensional vector subspaces 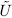 (over
(over 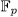 ) of the quotient space
) of the quotient space 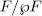 to finite dimensional subspaces
to finite dimensional subspaces 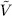 of the
of the 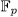 vector space
vector space 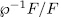 (where
(where 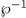 F is the inverse image under
F is the inverse image under 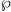 in some fixed separable closure
in some fixed separable closure 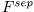 ). That is to say
). That is to say
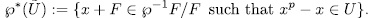
Finally if instead of 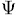 we consider the map
we consider the map
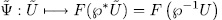 ,
,one can see that, one such n-dimensional subspace 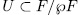 corresponds, in the notation of Theorem 1.5 to a subgroup
corresponds, in the notation of Theorem 1.5 to a subgroup 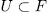 with
with 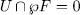 that is a "section" of
that is a "section" of 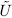 in the sense that
in the sense that 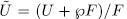 . Therefore, if
. Therefore, if 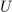 and
and 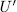 are subgroups of
are subgroups of  such that:
such that:
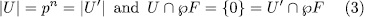
then, the following sentences are equivalent.
(Observe that
exactly when
( more accurately, when
and
are the same subspace of
.)) Moreover, if
, then
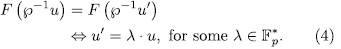
 such that
such that
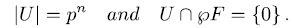
Then, the extension 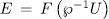 is an elementary abelian
is an elementary abelian  -extension of
-extension of  of exponent
of exponent  .
.
Prooƒ: first observe that since E is the splitting field of the set of polynomials 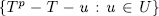 then the extensions
then the extensions 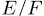 is a Galois extensions. On the other hand, since U is an additive subgroup of
is a Galois extensions. On the other hand, since U is an additive subgroup of  and char(F) =
and char(F) =  , then there exists
, then there exists 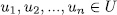 nonzero elements such that
nonzero elements such that
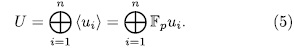
We can find 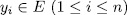 , such that
, such that 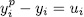 . Now, by Theorem 1.3 we have that
. Now, by Theorem 1.3 we have that
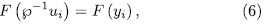
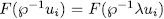 for each
for each 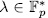 (Remark 1.6) we obtain
(Remark 1.6) we obtain
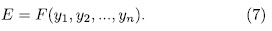
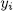 is a root of
is a root of 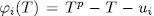 , then the extension
, then the extension 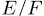 is finite. In order to prove that
is finite. In order to prove that 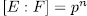 , first observe that,
, first observe that,
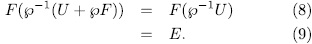
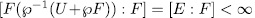 , by Theorem 1.5 we obtain
, by Theorem 1.5 we obtain 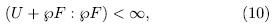
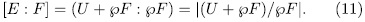
But
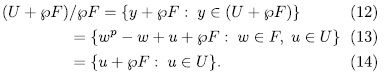
So, for 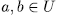 , since
, since 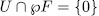 then
then
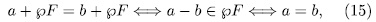
consequently, 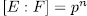 . Next we prove that
. Next we prove that 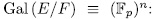 For
For 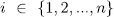 we define
we define 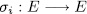 as follows,
as follows,
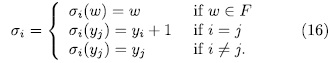
Observe that 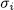 is the identity on
is the identity on
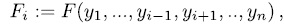
Therefore by Theorem 1.3, the polynomial 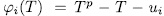 is irreducible over
is irreducible over 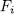 (otherwise
(otherwise 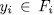 and
and 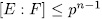 which is a contradiction) hence the
which is a contradiction) hence the 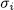 are actually well defined. Now it clear that each
are actually well defined. Now it clear that each 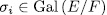 and
and 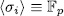 , also
, also
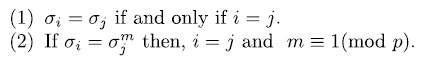
In fact, if 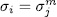 then,
then,
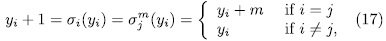
it follows that i = j and 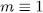 (mod
(mod  ). Therefore
). Therefore
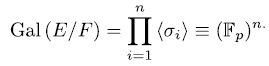
The converse of the Theorem 1.7 also holds. To prove it, we need the following lemma.
Lemma 1.8. Suppose that L/M is finite Galois extension with Galois Group of the form
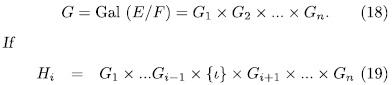
where
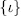 is the
is the 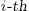 coordinate and
coordinate and 
then

Prooƒ: see {Ro} Corollary 5.5.4.
Theorem 1.9. If
 is an elementary abelian
is an elementary abelian  -extension of
-extension of  of degree
of degree 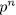 , then
, then

for some additive subgroup U of  which satisfies (3).
which satisfies (3).
Prooƒ: since 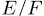 is an elementary abelian extension of degree
is an elementary abelian extension of degree 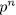 , then
, then
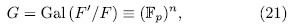
thus, 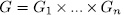 , where each
, where each 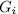 has order
has order  . Let us define for
. Let us define for 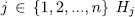 and
and 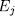 , be as in the Lemma 1.8 (a)
, be as in the Lemma 1.8 (a)
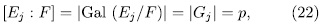
consequently, by Theorem 1.3. there exist 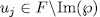 such that
such that 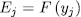 for some
for some 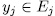 with
with 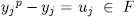 , which amounts to,
, which amounts to, 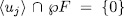 . Observe that
. Observe that  and since
and since 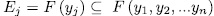 , from Lemma 1.8 (b),
, from Lemma 1.8 (b), 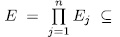
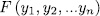 , and therefore
, and therefore
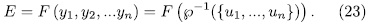
We now claim that  are linearly independent over
are linearly independent over 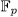 . In fact suppose there is a non-trivial linear combination
. In fact suppose there is a non-trivial linear combination 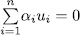 ,with
,with 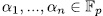 , then
, then
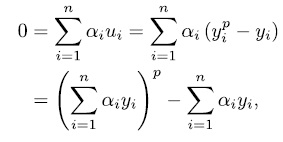
hence 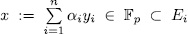 . Now if we assume that
. Now if we assume that 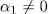 then
then 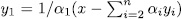 and since, for
and since, for 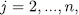 , we have that
, we have that 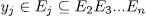 , then
, then 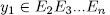 . On the other hand by Lemma 1.8,
. On the other hand by Lemma 1.8, 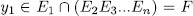 , consequently
, consequently 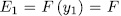 which is a contradiction since
which is a contradiction since 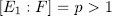 . Therefore
. Therefore 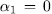 . Similar arguments will lead us to prove that
. Similar arguments will lead us to prove that 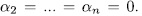 . Let U be the subgroup generated by
. Let U be the subgroup generated by 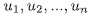 . Then by (23),
. Then by (23), 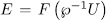 therefore only remains to prove that
therefore only remains to prove that 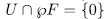 . In fact, if
. In fact, if 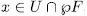 , then
, then 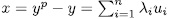 with
with 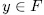 and each
and each 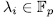 . Therefore it is enough to prove that
. Therefore it is enough to prove that 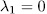 . For this end, observe that
. For this end, observe that
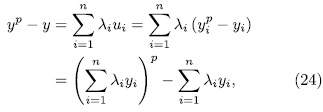
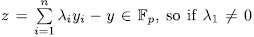 , we have that
, we have that
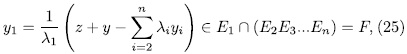
which is a contradiction.
Theorem 1.10. Let U be an additive subgroup of  such that
such that
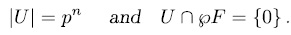
If 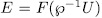 , then there exit
, then there exit 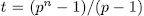 - intermediate fields
- intermediate fields 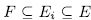 such that
such that 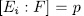 , where
, where 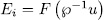 with
with 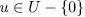 .
.
Prooƒ: if 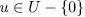 , then
, then 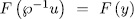 with
with 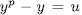 and by Theorem 1.3,
and by Theorem 1.3,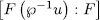 is either 1 or
is either 1 or  . but if
. but if 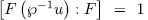 , then
, then 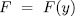 therefore
therefore 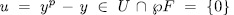 which is a contradiction with the choice of u, hence
which is a contradiction with the choice of u, hence 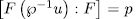 . On the other hand, if
. On the other hand, if 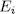 is a subfields such that
is a subfields such that 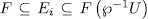 and
and 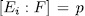 then by Theorem 1.3,
then by Theorem 1.3, 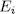 is the splitting field of one irreducible polynomial of the form
is the splitting field of one irreducible polynomial of the form 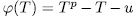 - for some
- for some 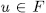 . Now, since
. Now, since 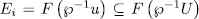 then by Remark 1.6 we have that
then by Remark 1.6 we have that 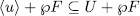 hence
hence 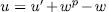 , for some
, for some 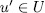 and
and 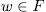 , from which
, from which 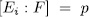 ,for some
,for some 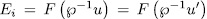 for some
for some 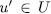 . In sum each subfield
. In sum each subfield 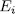 such that
such that 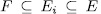 and
and 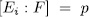 has the form
has the form 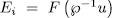 for some
for some 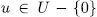 . Finally by Remark 1.6 we obtain the number of these subfields.
. Finally by Remark 1.6 we obtain the number of these subfields.
Theorem 1.11. Let K be a field of characteristic p > 0 an F/K an algebraic function field of transcendence degree one over K, with constant field K and genus g(F). Consider an elementary abelian extension E/F of degree pn such that K is also the constant field of E. denote by 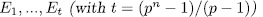 the intermediate fields
the intermediate fields 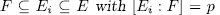 and by g(E) (resp
and by g(E) (resp 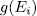 ) the genus of
) the genus of 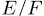 (resp
(resp 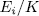 ). Then
). Then
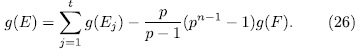
Prooƒ: Let
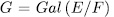 . For a subgroup
. For a subgroup 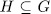 consider the fixed field
consider the fixed field 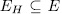 whose genus
whose genus 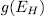 is denoted by
is denoted by 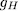 and the trace idempotent
and the trace idempotent 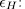
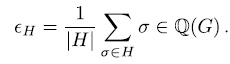
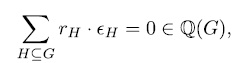
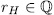 , because in this case genera would satisfy the same relation (see[Ka])
, because in this case genera would satisfy the same relation (see[Ka])
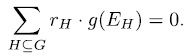
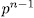 . In fact, by one side, for
. In fact, by one side, for 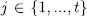 the Galois group
the Galois group 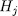 of the extension
of the extension 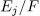 is one of such subgroups. On the other hand, if
is one of such subgroups. On the other hand, if 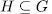 is subgroup such that
is subgroup such that 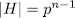 then since
then since 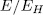 is a Galois extension with
is a Galois extension with 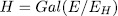 , we have
, we have 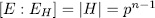 from which we get
from which we get 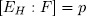 and
and 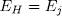 for some
for some 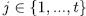 consequently,
consequently,
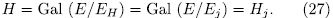
Now we shall show that any 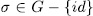 is contained in precisely t subgroup
is contained in precisely t subgroup 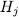 . In fact, each
. In fact, each 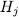 has the form
has the form
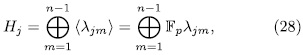
where each 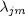 has order
has order  and the set
and the set 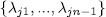 is a basis of
is a basis of 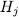 over
over 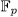 . Now, if
. Now, if 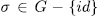 , then
, then 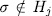 if and only if
if and only if 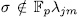 for
for 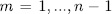 . That is to say, there exist
. That is to say, there exist 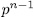 subgroups Hj such that
subgroups Hj such that  . In other words σ is contained in precisely
. In other words σ is contained in precisely 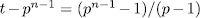 subgroup
subgroup 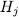 of G, therefore
of G, therefore
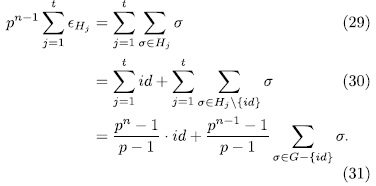
But from 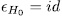 and
and
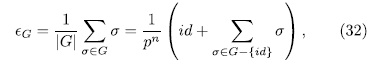
It follows that, 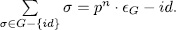 . Thus
. Thus
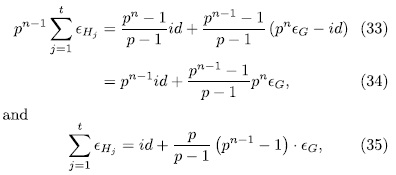
Which amounts to, we have the following relation in 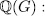
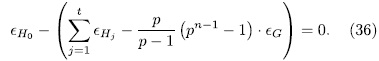
The theorem now follows from Kani's result.
Observe that the intermediate extension 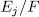 mentioned in Theorem 1.10 is an Artin-Schreier extension, whose genus,
mentioned in Theorem 1.10 is an Artin-Schreier extension, whose genus, 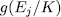 can be computed by [[ST], III.7.8]. This takes us to determine explicitly such intermediate field, which we will call Artin-Schreier intermediate subfields, for which we give the following results generalizing Propositions 1.1 and 1.2 in ([G-S]).
can be computed by [[ST], III.7.8]. This takes us to determine explicitly such intermediate field, which we will call Artin-Schreier intermediate subfields, for which we give the following results generalizing Propositions 1.1 and 1.2 in ([G-S]).
Before that, we should give a definition. We call a polynomial of the specific form

 = char (K)) an additive polynomial over K. observe that
= char (K)) an additive polynomial over K. observe that 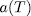 is separable if and only if
is separable if and only if 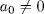 .
. Theorem 1.12. Let
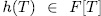 be a separable, monic, additive polynomial of degree
be a separable, monic, additive polynomial of degree 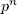 , with its roots in F. If E/F is an elementary abelian
, with its roots in F. If E/F is an elementary abelian  -extension of degree
-extension of degree 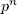 , then there exists an element
, then there exists an element 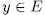 such that
such that 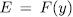 whose minimal polynomial over
whose minimal polynomial over  has the form
has the form 
Prooƒ: Let us consider the set
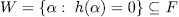 , it is clear that W is a vectorial space over
, it is clear that W is a vectorial space over 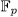 , moreover W is an additive finite subgroup of F. Now, since each cyclic subgroup of W is order 1 or
, moreover W is an additive finite subgroup of F. Now, since each cyclic subgroup of W is order 1 or  , then there exist nonzero elements
, then there exist nonzero elements 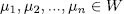 such that
such that 
and, the set
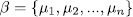 is a basis of W over
is a basis of W over 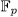 . Now from Lemma 1.8 we can choose
. Now from Lemma 1.8 we can choose 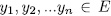 such that
such that 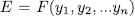 , with
, with 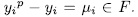 . If we define the
. If we define the 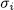 for
for 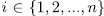 as in (16), it is clear that each
as in (16), it is clear that each 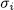 is an element of order
is an element of order  of Gal (E/F) and therefore
of Gal (E/F) and therefore 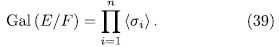
On the other hand, since
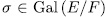 , then σ has a unique representation
, then σ has a unique representation 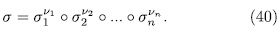
With
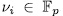 , then the action of σ over the element
, then the action of σ over the element 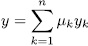 is given by
is given by
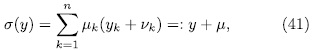
where 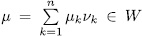 . It follows from (40) that
. It follows from (40) that 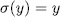 if and only if
if and only if 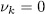 for k = 1,2,â¦,n, that is,
for k = 1,2,â¦,n, that is, 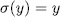 if and only if
if and only if 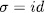 , and therefore
, and therefore 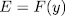 . On the other hand, if
. On the other hand, if 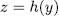 and
and 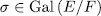 then, since
then, since 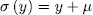 , for some
, for some 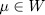 , we have
, we have
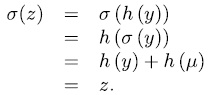
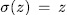 and therefore
and therefore 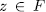 , consequently y is a root of the monic polynomial
, consequently y is a root of the monic polynomial 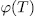 whose degree is
whose degree is 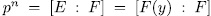 . This implies
. This implies 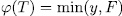 .
. Reciprocally we have:
Theorem 1.3. Let 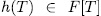 be a separable, monic, additive polynomial of degree
be a separable, monic, additive polynomial of degree  n, with its roots in
n, with its roots in  and
and 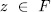 such that the polynomial
such that the polynomial 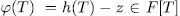 is irreducible over
is irreducible over  , then the extension
, then the extension 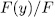 where
where 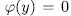 is an elementary abelian
is an elementary abelian  -extension of degree
-extension of degree  n. The intermediate subfield
n. The intermediate subfield 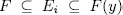 with
with 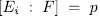 , have the form
, have the form 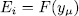 where,
where, 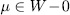 with
with 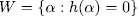 and each
and each 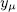 satisfies the equation
satisfies the equation 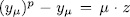 therefore
therefore 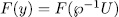 , with
, with 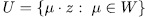
Prooƒ: It is clear that
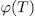 is the minimal polynomial for y over
is the minimal polynomial for y over  . Now, for each
. Now, for each 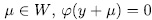 then all roots of the polynomial
then all roots of the polynomial 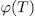 have the form
have the form 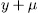 with
with 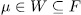 , and therefore
, and therefore  (y) is the splitting field of the polynomial
(y) is the splitting field of the polynomial 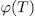 . On the other hand since
. On the other hand since 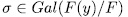 permutes the roots of
permutes the roots of 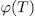 then
then 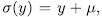 for some
for some 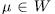 , therefore, the application
, therefore, the application 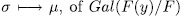 , into group
, into group 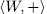 is an isomorphism, that is to say,
is an isomorphism, that is to say, 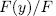 is an elementary abelian
is an elementary abelian  -extension of degree
-extension of degree 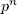 .
. Now, if 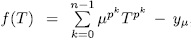 , then
, then 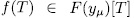 and
and 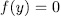 it follow that
it follow that 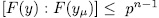 . On the other hand, since
. On the other hand, since 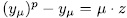 then
then 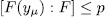 and therefore
and therefore
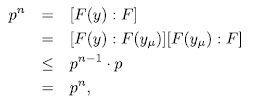
consequently 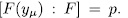 It is say,
It is say, 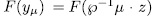 Now, by Remark 1.6 there exist
Now, by Remark 1.6 there exist 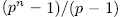 such subextensions
such subextensions 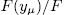 and therefore
and therefore 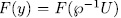 where
where 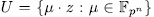 . Finally by Theorem 1.10 there exist exactly
. Finally by Theorem 1.10 there exist exactly 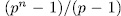 intermediate fields
intermediate fields 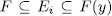 with
with 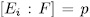 therefore such
therefore such 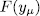 must be one of the
must be one of the 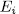 .
.
2. An application to the construction of curves over finite fields
It is well known that algebraic function fields over finite fields have many applications in coding theory, and the latter is closely related to cryptography, see for example [N-Ch]. In this section we exhibit a method to construct algebraic function fields over finite fields (algebraic curves) with many rational places (rational points).
Let  be a prime number,
be a prime number, 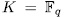 the finite field with
the finite field with 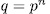 elements and
elements and 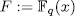 the rational function field over the finite field
the rational function field over the finite field 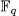 . By E/K we mean a function field of transcendence degree one over K , with constant field K. We denote by
. By E/K we mean a function field of transcendence degree one over K , with constant field K. We denote by 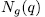 the maximum number of rational places of the function field E/K of genus g(E/K) = g. The Hasse-Weil bound implies
the maximum number of rational places of the function field E/K of genus g(E/K) = g. The Hasse-Weil bound implies
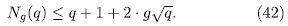
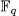 remained untouched for many years. In 1980 Goppa came up with the beautiful idea to associate an error-correcting code to a linear system on a curve over a finite field, see [Go]. In order to construct good codes one needs function fields with many places and thus Goppa's work led to a revival of interest in rational points on function fields (algebraic curves) over finite fields. Applications in cryptography and recent constructions of quasi-random points sets also require curves with many points and added further impetus to work in the field.
remained untouched for many years. In 1980 Goppa came up with the beautiful idea to associate an error-correcting code to a linear system on a curve over a finite field, see [Go]. In order to construct good codes one needs function fields with many places and thus Goppa's work led to a revival of interest in rational points on function fields (algebraic curves) over finite fields. Applications in cryptography and recent constructions of quasi-random points sets also require curves with many points and added further impetus to work in the field. In 1981 Ihara showed in [1] that
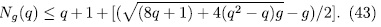
 this bound is better that Weil`s bound and gives the asymptotic bound
this bound is better that Weil`s bound and gives the asymptotic bound
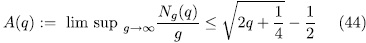

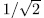 times the asymptotic Ihara bond (44) we think that it is reasonable to put this qualification as requirement to filter out curves which should be considered 'poor'.
times the asymptotic Ihara bond (44) we think that it is reasonable to put this qualification as requirement to filter out curves which should be considered 'poor'. To begin our construction, let us benote by 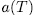 the additive polynomial
the additive polynomial
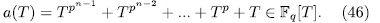
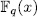 of the kind
of the kind 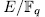 where
where 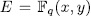 is defined by the equation:
is defined by the equation:
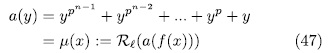
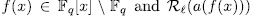 denote the remainder of the Euclidean division of the polynomial
denote the remainder of the Euclidean division of the polynomial 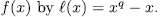 . That is to say extensions of the kind,
. That is to say extensions of the kind, 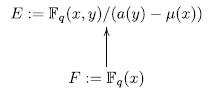
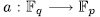 . More precisely we have.
. More precisely we have. Theorem 2.1. The polynomial 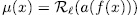 defined as (47)has the following property:
defined as (47)has the following property:
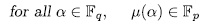
Proof. It is enough to prove that
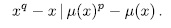
Since
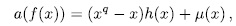
for some polynomial 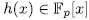 , then
, then
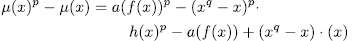
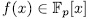 and
and 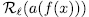 is additive, the result follows.
is additive, the result follows. Remark 2.2. Observe that in accordance with Theorem 2.1, we have that, for 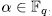 , the equation
, the equation
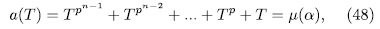
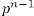 solutions in
solutions in 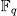 , therefore the induced curve by the function field E/K has at least
, therefore the induced curve by the function field E/K has at least 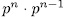 places of degree one. This leads us to expect to get good curves.
places of degree one. This leads us to expect to get good curves. The following result provides us a relationship among the genus of the function field E/K and the genus of the Artin-Schreier intermediate subfields 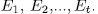
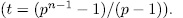 .
.
Theorem 2.3. With the previous notations, the genus of E/K is given by
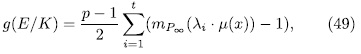
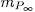 is defined as follows:
is defined as follows:
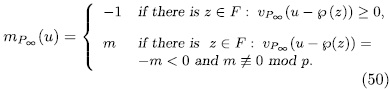
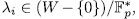 with
with 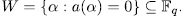
Remark 2.4. Lemma III.7.7 in [ST], guarantees that we can exclude the case
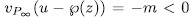 for an integer
for an integer 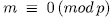 in the above definition for
in the above definition for 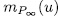
Indeed, first observe that from ([ST], i.4.18) together with Theorem 1.11 we have that:
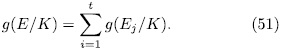
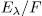 has the form
has the form

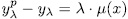 and
and 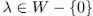 . Now, since
. Now, since 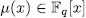 , then each of
, then each of  different from
different from 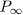 is unramified in
is unramified in 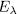 , in this way, from ([ST], III.7.8) the genus of
, in this way, from ([ST], III.7.8) the genus of 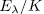 is given by
is given by
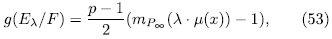
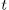 different subfields of the Artin-Schreier, then there are
different subfields of the Artin-Schreier, then there are  in W such that, each one those the Artin-Schreier subfields have the form
in W such that, each one those the Artin-Schreier subfields have the form 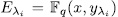 . Finally, from (53) and (51) we have the result.
. Finally, from (53) and (51) we have the result. Next, we exhibit a technique that allow us to count the rational places of E/K. for this, we will denote by
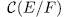 , the induced curve by the function field E/K.
, the induced curve by the function field E/K. Lemma 2.5. Let us consider the polynomial
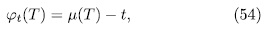
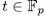 and
and 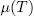 are defined as in (47). Then, for
are defined as in (47). Then, for 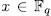 , there exist
, there exist 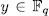 such that
such that 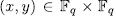 - belongs to
- belongs to 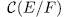 , if and only if
, if and only if 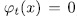 , for some
, for some 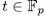 .
. Prooƒ: Let us suppose that exists
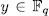 such that (x, y) belongs to
such that (x, y) belongs to 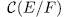 , it is to say
, it is to say 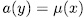 . Since
. Since 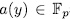 , then by taking
, then by taking 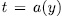 we obtain the desired result. Reciprocally, if
we obtain the desired result. Reciprocally, if 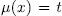 for some
for some 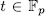 and since the function a is surjective ([L-N], 2.23), then
and since the function a is surjective ([L-N], 2.23), then 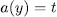 for some
for some 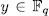 , it is to say,
, it is to say, 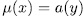 .
. Lemma 2.6. With the above notations,
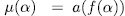 for all
for all 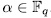 .
. Prooƒ: By the division algorithm, there exists 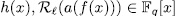 such that
such that
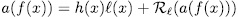
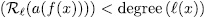 degree
degree 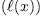 . Then
. Then
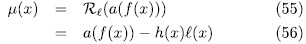
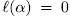 for all
for all 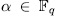 , we have
, we have 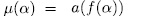
As consequence of all the above mentioned we have,
Theorem 2.7. The number of rational places of the elementary abelian p-extension defined by (47) is given by
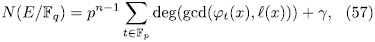
Prooƒ: For fixed 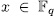 , we have that (x, y) is a rational point of the curve
, we have that (x, y) is a rational point of the curve 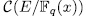 if and only if
if and only if 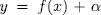 where
where 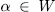 . In fact, if (x, y) is a rational point of
. In fact, if (x, y) is a rational point of 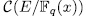 then
then
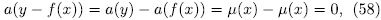
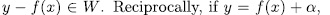 where
where 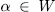 , then
, then
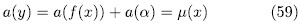
Now, for each
 such that
such that  , we have
, we have 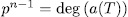 places of degree one of E. Additionally, since for all place
places of degree one of E. Additionally, since for all place  of
of  different of
different of 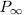 , P is unramified in E, then
, P is unramified in E, then 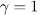 or 0. Therefore,
or 0. Therefore,
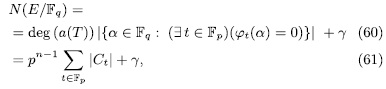
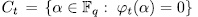 y
y 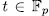 . On the other hand, if
. On the other hand, if 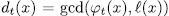 , then
, then 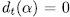 if and only if
if and only if 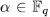 and
and 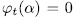 and since
and since 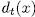 is separable, then
is separable, then 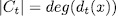 .
. 3. Examples
In this section we give examples of elementary the Abelian p-extensions of the kind given by (47). We will to consider the particular case when n is odd and 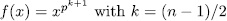 and we will determine the genus and the number of rational places of these extensions using the formulas (49) and (57).
and we will determine the genus and the number of rational places of these extensions using the formulas (49) and (57).
Example 3.1 It p = 2 and n =3, then k =1, q =8. Also,
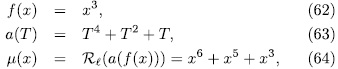
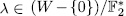 we have
we have 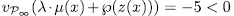 and since
and since 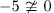 then, from ([ST], III.7.8), we obtain
then, from ([ST], III.7.8), we obtain 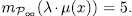 . Observe that this value is independ of the root λ, therefore there exist exactly 3 different the Artin-Schreier extensions generated by such roots, and in accordance with (49) we have
. Observe that this value is independ of the root λ, therefore there exist exactly 3 different the Artin-Schreier extensions generated by such roots, and in accordance with (49) we have
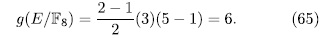
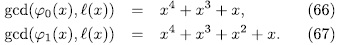
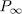 of F is the only place that ramifies in the extension E/F then by (57) we have
of F is the only place that ramifies in the extension E/F then by (57) we have
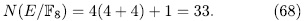
Example 3.2. Taking p = n = 3, then q = 27 and k = 1. Also,
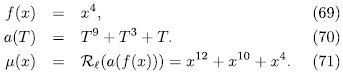
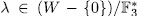 we have,
we have, 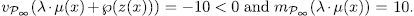 . Therefore
. Therefore
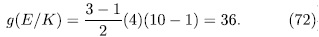
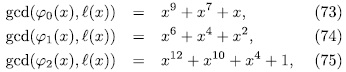
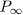 is totally ramified and rational in
is totally ramified and rational in 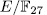 then we have
then we have
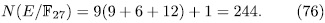
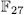 of genus 36 having more that 244 rational places (see [VV]).
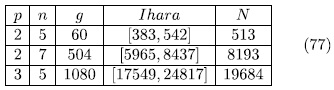
of genus 36 having more that 244 rational places (see [VV]). The following table contains the values obtained for the genus and the number of rational points by taking different values for p and n, also we compare this values obtained with the Ihara's bound
Acknowledgements. The authors deeply appreciate the helpful comments suggestions made by the referees.
References [ Links ] 1991.
[L-N] Lidl Rudolf and Niederreiter Harald. Introduction to finite fields and their applications. Cambridge university press, [ Links ] 1994.
[Go] V.D. Goppa, Codes on algebraic curves. Sov Math.Dokl 24 (1981), 170-172. [ Links ]
[La] Lang Serge, Algebra, Adisson Wesley Publishing Company, [ Links ] 1970.
[Ka] Kani Ernest, Relations between the genera and between the Hasse-Witt invariants of Galois covering of curves, Canad. Math. Bull, Vol 28, pag 321-327, [ Links ]1985.
[N-Ch] Harald Niederreiter, huaxiong Wang and Chaoping Xing, Function Fields over Finite Fields and their applications to Cryptography, Springer- verlag. [ Links ] 2007
[I] Ihara Y. Some remarks on number of rational points of algebraic curves over finite fields. J Fac Sci Tokyo 28 (1981), p.721-724. [ Links ] [Ro] Roman Steve. Field Theory. Springer-Verlag, [ Links ] 1991
[ST] Stichtenoth Hennig. Algebraic functions fields and codes. Springer- verlag, [ Links ] 1993.
[VV] Van Der Geer Gerard and Van Der Vlugt Marcel. Tables of curves with many points. [Online], http://www.science.uva.nl/ geer. [ Links ]
Recibido el 4 de noviembre de 2009
Aceptado para su publicación el 21 de junio de 2010
Versión revisada recibida el 5 de marzo de 2012














