INTRODUCTION
This article is the product of the work of the Master’s thesis in Criminal Procedural Law at the Universidad Autónoma Latinoamericana (Colombia), entitled “Reasonable inference as a standard of proof in criminal matters in Colombia” (Jaramillo, Mosquera & Jaramillo, 2021), completed in June 2021, and of the article entitled “Evidence and inference, a reflection” (Jaramillo & Vargas, 2020), published in December 2020 in the journal Ámbito Jurídico. Both publications were funded by Total Jurídica S.A.S. law firm.
The problem that arises in this article is related to the methodology, procedure or algorithm that is used by the judge in the stages of the evidentiary activity as the basis of the judicial decision (Vargas, 2019). This methodology, procedure or algorithm is, on occasions, a “black box” in relation to the adequate motivation that must be reflected in the sentence that decides the judicial process.
The purpose of this article is to propose a methodology, procedure or algorithm that allows organizing the judge’s thinking, in the motivation of the sentence that decides the judicial trial, from the proof of the facts to the hypotheses or allegations that are considered in the judicial trial.
The proposed methodology, procedure or algorithm is based on the chartmethod (Wigmore, 1937), on the chains of reasoning (Schum, 2016), on fuzzy logic (Zadeh, 1983), on the “on balance function” and the functioning of the cognitive assistant -Disciple-CD- (Tecuci, Schum, Marcu & Boicu, 2016), on the Baconian system of probabilities (Cohen, 2017) and on the acceptance mechanisms as active states of the human mind (Cohen, 2021).
Initially it is illustrated how the expert system called “Intelligent Judge” uses this methodology, procedure or algorithm, which assists the judge in the orderly construction of inferences or evidentiary arguments, from the proof of the facts to the hypotheses or allegations that are considered in the judicial process and that are the basis for the motivation of the sentence that decides the said trial (Vargas, Hincapié, Sepúlveda & Pabón, 2021) (Vargas, 2021).
Subsequently, the Baconian probability system is explained (Cohen, 2017), which, using fuzzy qualifiers (Zadeh, 1983; Tecuci et al., 2016), is used by the expert system “Intelligent Judge” to calculate the individual and joint evidentiary weight that evidence gives to the facts and to the hypotheses and allegations, respectively.
Finally, in the conclusions, the above is illustrated by example, using the respective link.
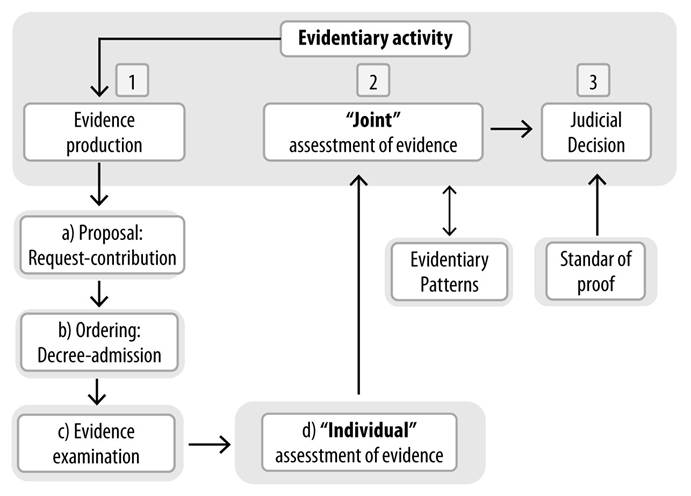
1. STAGES OF THE EVIDENTIARY ACTIVITY AS A FRAMEWORK FOR THE EVIDENTIARY REASONING USED BY THE “INTELLIGENT JUDGE” EXPERT SYSTEM
The analysis carried out by the “Intelligent Judge” expert system is based on the estimation of the probability based on the evidence, hypotheses or allegations, which are raised by the plaintiff in the civil process, or on the theory adduced by the prosecution in relation to the case in the criminal trial. This analysis is carried out in the stages of the evidentiary activity of evidence production, ordering, examination and assessment by assigning probability values to the relevant facts and to the pertinent and credible evidence. With these assigned values, the expert system calculates the evidentiary weight of each evidence, in relation to the facts that support the hypothesis or allegation, and then performs the calculation of the evidentiary weight of the evidence as a whole, in relation to the hypothesis or allegation. This analysis answers the question: How likely is the hypothesis or allegation raised by the party that has the burden of proof in the judicial trial?
Next, the evidentiary reasoning adopted by the judge is illustrated using the expert system “Intelligent Judge” in each of the stages of the evidentiary activity.
1.1 First Stage of the Evidentiary Activity: Production of Evidence
In the Colombian legal system, the procedural rule prescribes that the moment in which the parties have the opportunity to request or provide evidence of the facts that serve as support or foundation for the respective hypotheses or allegations that arise in the judicial process is the one of the allegation, the one of the answer to the allegation in a civil proceeding or the one of the charge in a criminal proceeding. At this stage, the judge is aware of the hypotheses or allegations raised by the parties, the facts in issue related to the said hypotheses or allegations, and the evidence related to said controversial facts.
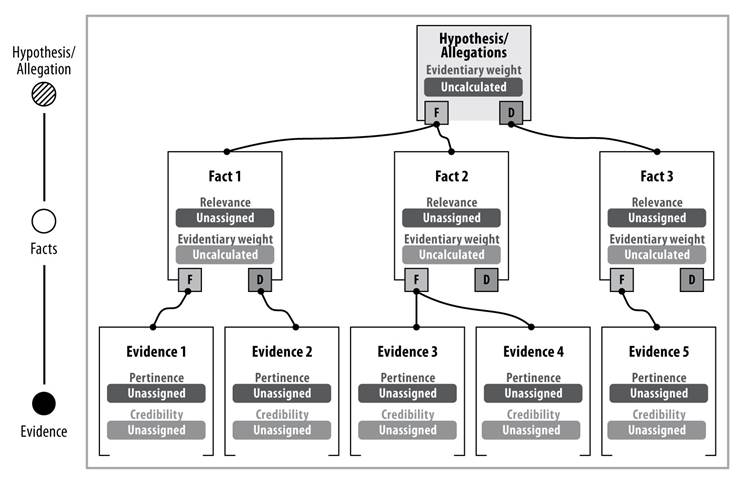
Source: own elaboration
Figure 2 Hypothesis or allegations, facts and evidence, are introduced in the “Intelligent Judge” expert system
Relevance of Facts
At this stage of the proposal, the judge interacts with the “Intelligent Judge” expert system, answering a question related to the relevance of the facts on which the parties base their hypotheses or allegations: If this fact raised by the party with the burden of proof is true, how likely is his/her hypothesis or allegation?
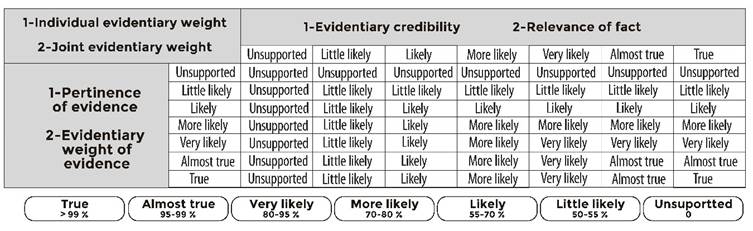
From figure 3, the judge assigns a representative concept, linguistically expressed -a “semantic differential” type of criterion-, and a probability value to the relevance of each of the facts raised by the party that has the burden of proof (Tecuci, Schum, Marcu, & Boicu, 2016). Suppose that the judge assigns a relevance value to this fact represented by the “very likely” criterion.

Source: own elaboration
Figure 3 Baconian probabilities with fuzzy qualifiers for the individual and joint evidentiary weight calculus
With this relevance value assigned with the “very likely” criterion, the “Intelligent Judge” expert system builds the rule of experience, which allows the judge to justify the relevance value assigned by him to each of the facts, in relation to the hypothesis or allegation of the party that has the burden of proof.
This rule of experience is formulated as follows: “If the fact is true, then it makes the hypothesis or allegation ‘very likely’.”
1.2 Second Stage: Ordering of Evidence
At this stage, the judge proceeds to decree and admit the evidence that has been requested and provided in the previous stage. Colombian procedural rules, in civil and criminal matters, prescribe what is related to the decree and the admission of evidence in the judicial process.1
Pertinence of Evidence
At this stage, the judge interacts with the “Intelligent Judge” expert system, answering a question related to the pertinence of the evidence on which the parties base the controversial facts in the judicial process: If this evidence proposed by the party with the burden of proof is true, how likely does this evidence make the fact it is intended to prove?
From figure 3, the judge assigns a representative concept, expressed linguistically -a “semantic differential” type of criterion-, and a probability value to the pertinence of each evidence (Tecuci et al., 2016). Suppose the judge assigns a pertinence value to this evidence represented by the “likely” criterion.
Taking into account this value of pertinence assigned with the “likely” criterion, the expert system “Intelligent Judge” builds the rule of experience, which allows the judge to justify the value of pertinence that he assigns to each evidence. This rule of experience is formulated as follows: “If the evidence of the fact is true, then it makes the fact ‘likely’.”
1.3 Third Stage of the Evidentiary Activity: Examination of Evidence
The principle of immediacy requires the judge to examine the evidence that have been decreed and admitted in the previous stage. Colombian procedural rules, in civil and criminal matters, prescribe what is related to the examination of evidence in the judicial process.2
At this stage, the judge assesses the credibility of each evidence, which is in accordance with what is prescribed in Colombian civil and criminal legislation.3
1.3.1 Evidence Credibility
At this stage, after the evidence has been examined, the judge interacts with the “Intelligent Judge” expert system, answering a question related to the credibility of the evidence on which the controversial facts in the judicial process are based: How likely is it that what says this proof, proposed by the party that has the burden of proof, is true? From figure 3, the judge assigns a representative concept, expressed linguistically -a “semantic differential” type of criterion-, and a probability value to the credibility of each evidence (Tecuci et al., 2016). Suppose the judge assigns a credibility value to this evidence represented by the “unlikely or little likely” criterion.
1.3.2 Evidentiary Weight of Each Piece of Evidence (Individual Assessment)
Taking into account the credibility and pertinence values assigned with semantic differential criteria to each one of the pieces of evidence in the previous stages (production and ordering), the “Intelligent Judge” expert system calculates the evidentiary weight that each evidence gives to each fact. This individual evidentiary weight is the least valuated semantic differential criterion, for pertinence and credibility, of those that each evidence has given to each of the facts (Cohen, 2017; Schum, 2016; Tecuci, Schum, Marcu & Boicu, 2016).
In the present case, the evidentiary weight that the evidence gives to this fact is the semantic differential criterion with the lowest value between “likely” (pertinence) and “unlikely or little likely” (credibility). Therefore, the evidentiary weight that the evidence gives to this fact is represented by the “unlikely or little likely” criterion (table 1).
1.4 Fourth Stage of the Evidentiary Activity: Assessment of the Evidence
The principle of unity that is enshrined in the Colombian Procedural Rule4 prescribes that, at this stage, the judge must assess the totality of the evidence, using rationality criteria and taking into account the evidentiary patterns of concordance and convergence that are presented among the various evidence.5
1.4.1 Evidentiary Weight of all the Evidence (Conjunct Assessment)
With the relevance value assigned by the judge to the facts in the second stage (ordering), represented by a specific semantic differential criterion, and with the value of the evidentiary weight that the evidence gave to the facts, represented by another semantic differential criterion, the “Intelligent Judge” expert system calculates the evidentiary weight that all the evidence, together, gives to the hypothesis or allegation.
The joint evidentiary weight is the semantic differential criterion of least value, for the relevance and the evidentiary weight, among the ones evidence gives to the fact (Cohen, 2017; Schum, 2016; Tecuci, Marcu, Boicu & Schum, 2016; Wigmore, 1937).
In the present case, the evidentiary weight that evidence gives to the hypothesis or allegation is the semantic differential criterion with the least value between “very likely” (relevance) and “unlikely or little likely” (evidentiary weight). The evidentiary weight that this evidence and this fact give to the hypothesis or allegation is represented by the “unlikely or little likely” semantic differential criterion. (Table 1).
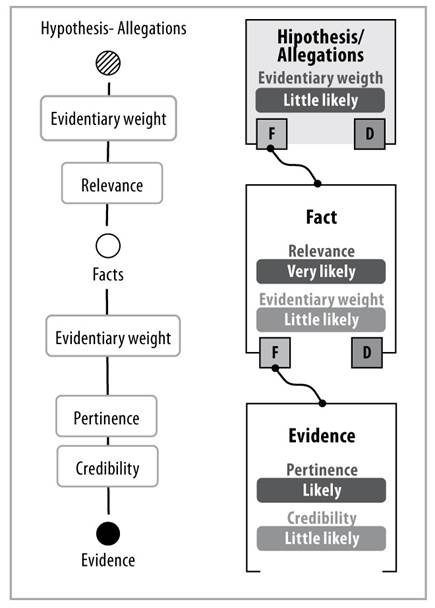
Source: own elaboration
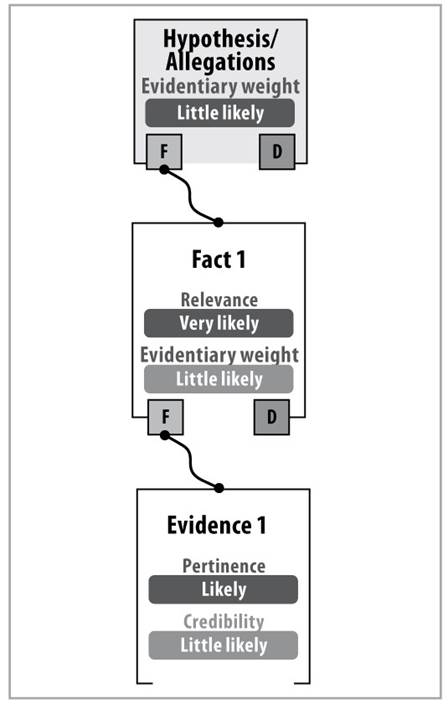
Figure 4 Assigned values of relevance, pertinence, and credibility. Calculus of the individual weight of evidence by the Intelligent Judge” expert system
Figure 4 shows that it is possible to have evidence that is not very credible (“little likely”), relevant (“likely”) and with little evidentiary weight (“little likely”), connected inferentially with a very relevant fact (“very likely”). Based solely on this evidence and on this fact, hypothesis or allegation of the party bearing the burden of proof6, it can be inferred that such evidence is little likely. This process is repeated for each of the facts and for each evidence that takes place in the judicial process.
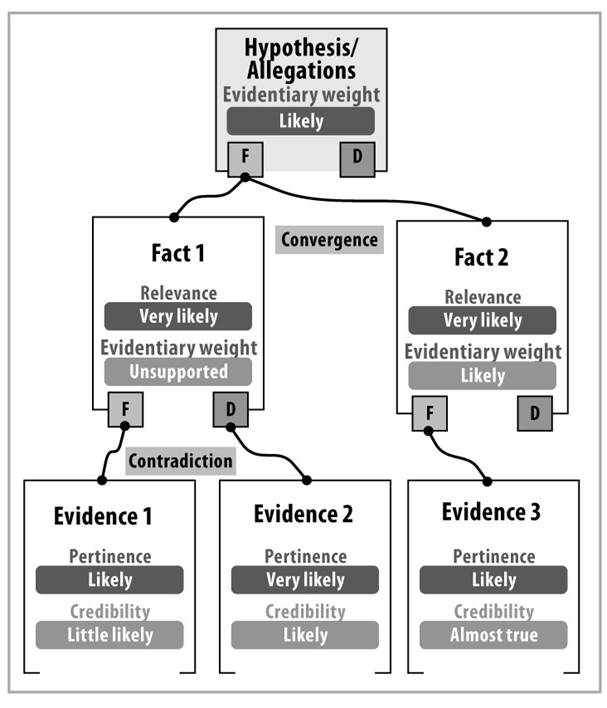
1.4.2 Evidentiary Patterns of Corroboration, Convergence, Contradiction and Evidentiary Conflict Used by the “Intelligent Judge” Expert System
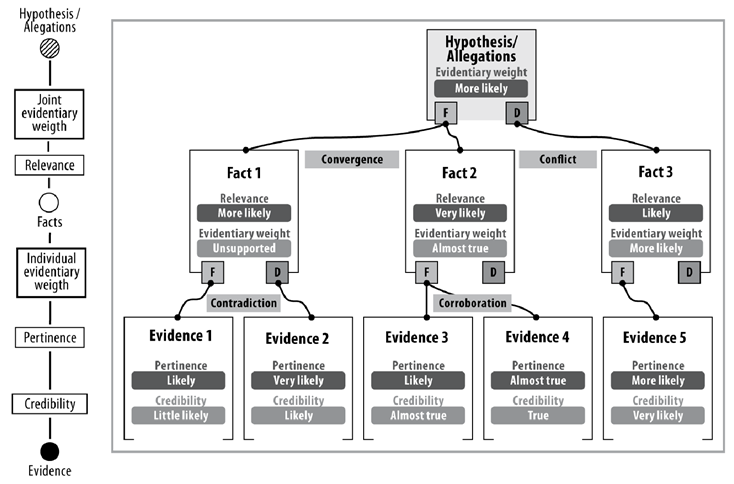
Source: own elaboration
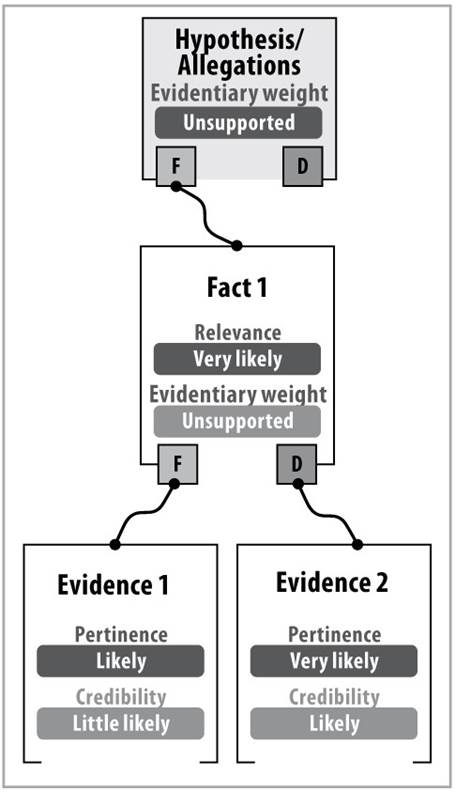
Figure 5 Corroboration, convergence, contradiction, and evidentiary conflict patterns used in the joint assessment by the “Intelligent Judge” expert system
Figure 5 shows five single pieces of evidence, three facts and a hypothesis or allegation. Evidence 1 favors (F) fact 1. Evidence 2 disfavors (D) fact 1. These two pieces of evidence show a pattern of contradiction in relation to fact 1. Evidence 3 favors (F) fact 2. Evidence 4 favors (F) fact 2. These two pieces of evidence show a corroborative pattern in relation to fact 2. Pieces of evidence 1, 3 and 4 favor (F) different facts (fact 1 and 2, respectively) which favor (F) the same hypothesis or allegation. These three pieces of evidence show a pattern of evidentiary convergence in relation to the hypothesis or allegation of the party that has the burden of proof. Evidence 5 favors (F) fact 3, which, in turn, disfavors (D) the hypothesis or allegation of the party bearing the burden of proof. Pieces of evidence 1, 3 and 4 favor (F) different facts (fact 1 and 2, respectively) and favor (F) the same hypothesis or allegation. Pieces of evidence 1, 3 and 4, which favor (F) the hypothesis or allegation of the party with the burden of proof, show a pattern of evidentiary conflict with evidence 5, which disfavors (D) the said hypothesis or allegation.
Based solely on these five pieces of evidence and the three illustrated facts, the evidentiary weight of the hypothesis or allegation of the party bearing the burden of proof is represented by the “more likely” semantic differential criterion.
1.5 The Judicial Decision
Once the expert system, using the evidentiary standards of corroboration, convergence, contradiction and evidentiary conflict, has calculated the evidentiary weight that all the pieces of evidence, conjointly, give to the hypothesis or allegation of the party that has the burden of proof, the judge proceeds to decide on the sentence in accordance with the respective standard of proof that has been adopted in civil or criminal matter (Figure 6).
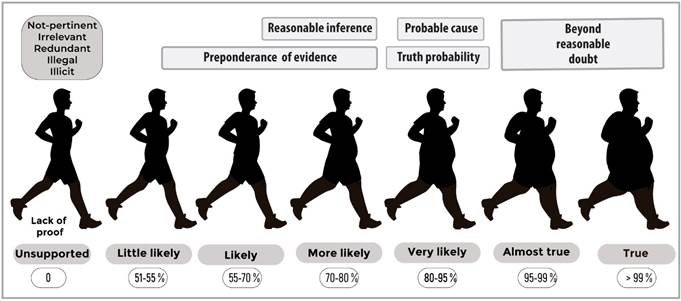
Source: own elaboration
Figure 6 Standards of proof employed in the judicial decisión by the “Intelligent Judge” expert system
Figure 6 shows that if the evidence, in relation to a fact, is not-pertinent, irrelevant, redundant, illegal or illicit, its probability value is 0, and the fact that was going to be proved with it remains unsupported by lack of proof (Cohen, 2017).
2. THE DOMESTICATION OF UNCERTAINTY AND IMPRECISION
Uncertainty governs the decision-making process that is performed by the judge regarding evidence. This uncertainty is related to the proving of the disputed facts by the parties in the judicial process. Given that these events are events of the past, and about which the judge has no knowledge, the evidence thereof only allows the judge to have probable knowledge in relation to their occurrence or non-occurrence. This probable knowledge can be measured or graded by various probability systems. However, since the word probable is vague and imprecise, it is equally necessary to use logical systems that allow uncertainty and imprecision to be “tamed”.
2.1 The Baconian System of Probabilities
To manage uncertainty, the “Intelligent Judge” expert system uses the Baconian probability system proposed by Jonathan Cohen, which allows to graduate the uncertainty associated with the decision-making process ran by the judge.
This Baconian system of probabilities is a means of graduating the “provability” -a term used by Cohen- of the hypotheses or allegations proposed by the party bearing the burden of proof in the judicial trial.
In the Baconian system of probabilities, the probability of the hypotheses or allegations made by the party bearing the burden of proof depends on the completeness with which the credible and pertinent evidence supports, inductively, the “provability” of the relevant facts with regards to such hypotheses or allegations.
2.1.1 Properties of the Baconian Probability System
Below, are illustrated some properties of the Baconian system of probabilities that allow the calculation of the evidentiary weight, individually and jointly, of the evidence in relation to the facts and the hypotheses or allegations that are proposed by the parties in the judicial trial.
2.1.1.1 Conjunction Rule
“The Baconian probability of a conjunction of probabilities (intersection) will never be less than the smallest Baconian probability of its conjuncts.” (Tecuci et al., 2016)7*
From the above it follows that “The probability of a fact, based on the relevant and credible evidence, is never less than the smallest probability of the relevance and of the credibility of said evidence.” (Tecuci et al., 2016)8 (See 1.3.2 above). Figure 4 illustrates how, based on the values of relevance (“likely” semantic differential criterion) and credibility (“little likely” semantic differential criterion) of the evidence, the evidentiary weight that said evidence gives to the fact is the one represented by the “little likely” semantic differential criterion.
The probability of a hypothesis or allegation, based on the relevance of the fact and the evidentiary weight of the evidence that supports it, is never less than both the smallest probability of the relevance of the fact and the one of the evidentiary weight of the evidence that supports it.9 (See 1.4.1 above). Figure 4 illustrates how, based on the values of relevance of the fact (“very likely” semantic differential criterion) and evidentiary weight (“little likely” semantic differential criterion) that the evidence gives to the fact, the evidentiary weight that said evidence gives to the hypothesis or allegation is represented by the “little likely” semantic differential criterion.
Table 1 illustrates the balance of probabilities that can be established for:
The individual evidentiary weight that the evidence gives to the fact, based on the relevance and the credibility of the evidence.
The joint evidentiary weight that the evidence gives to the hypothesis or allegation, based on the relevance of the fact and the evidentiary weight that the evidence gives to the fact.
Table 1 shows the various combinations that can be presented for the evidence, in relation to the values of relevance and credibility, and for the evidentiary weight that evidence gives to the facts and their relevance.
In other words, it is possible to have a (little, very or not at all) credible and (little, very or not at all) relevant evidence, giving (little, much or no) weight to a (little, very or not at all) relevant fact in relation to a hypothesis or allegation raised in a judicial trial.
2.1.1.2 Disjunction Rule
“The probability of a disjunction of probabilities (union) is equal to the largest Baconian probability of its disjoints.” (Tecuci et al., 2016)
From the foregoing it follows that “The probability of a fact that is favored by two or more pieces of evidence, with different evidentiary weight, is equal to the Baconian probability with the greater evidentiary weight of its disjunctions.” (Tecuci et al., 2016)10
Table 2 Baconian probabilities with fuzzy qualifiers for the calculation of the conjunct evidentiary weight of consonant evidence
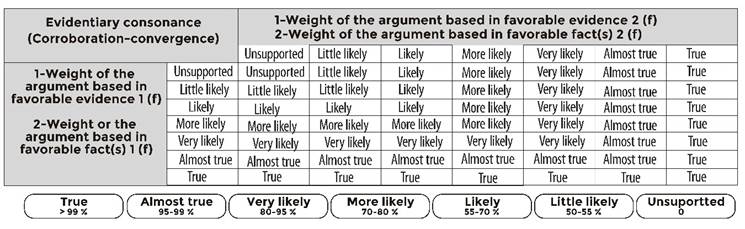
Source: own elaboration.
Figure 5 and table 2 illustrate how the values of pertinence (“likely” semantic differential criterion) and credibility (“almost true” semantic differential criterion) of evidence 3, the evidentiary weight that it gives to fact 2 is represented by the “likely” semantic differential criterion.
For the values of pertinence (“almost true” semantic differential criterion) and credibility (“true” semantic differential criterion) of evidence 4, the evidentiary weight that it gives to fact 2 is represented by the “almost true” semantic differential criterion. The greatest evidentiary weight of these two pieces of evidence that favor fact 2 is represented by the “almost true” semantic differential criterion.
The foregoing corresponds to the evidentiary corroboration pattern illustrated above in 1.4.2 and in figure 5. The probability of a hypothesis or allegation that is favored by two or more facts that have different evidentiary weight is equal to the Baconian probability with the greater evidentiary weight of their disjunctions.11
Figure 5 and table 2 illustrate how the values of relevance (“very likely” semantic differential criterion) and evidential weight (“unsupported” semantic differential criterion) of conflicting pieces of evidence 1 and 2 show the evidentiary weight that they give to the hypothesis or allegation is represented by the “unsupported” semantic differential criterion. Similarly, for the relevance values (“very likely” semantic differential criterion) and evidential weight (“almost true” semantic differential criterion) of corroborating pieces of evidence 3 and 4, the evidentiary weight that they give to the hypothesis or allegation is represented by the “very likely” semantic differential criterion. The greatest evidentiary weight of these two facts that favor the same hypothesis or allegation is represented by the “almost true” semantic differential criterion. The foregoing corresponds to the evidentiary convergence pattern (consonance) illustrated above in 1.4.2, in figure 5 and in table 2.
2.1.1.3 Property of Negation
“If the Baconian probability of a hypothesis or allegation, based on evidence, is greater than 0, then the Baconian probability of the denial of said hypothesis or allegation, based on said evidence, is equal to 0.”(Schum, 2016).
If PB (Hparty/p1) = 1 then PB (non-Hcounterparty/p1) = 0.
This means that, if the Baconian probability of the hypothesis or allegation of the party bearing the burden of proof, based on the favorable evidence, is greater than 0, then the Baconian probability of the denial of the hypothesis or allegation of the counterparty, based on said favorable evidence, will be equal to 0.12 (figure 7).
The foregoing, until the counterparty produces and proposes an unfavorable evidence that equals or exceeds the degree or measure initially established by the party that has the burden of proof. If the counterparty does not propose an evidence that disfavors the hypothesis or allegation raised by the party that has the burden of proof, the denial of said hypothesis or allegation is unsupported due to lack of evidence. For this reason, the value of zero, in the Baconian probability system, means “lack of evidence.”
Assuming that the counterparty produces and proposes evidence 2, which challenges the credibility of evidence 1 to an equal or greater degree or measure, then fact 1 and the hypothesis or allegation of the party bearing the burden of proof are left unsupported and its value is 0.13 (figure 8).
If PB (Hparty/p1 and p2) = 0 then PB (non-Hcounterparty/p1 and p2) = 2.
Evidence 2 increases the probability of the denial of the hypothesis or allegation of the counterparty to a higher level, equal to 2, and the probability of the hypothesis or allegation of the party bearing the burden of proof falls to 0. First, one part of the balance was charged in favor of the hypothesis or allegation of the party bearing the burden of proof and the other was withdrawn, and then the opposite happened.
To the extent that the parties produce and propose various pieces of evidence, in relation to the relevant facts that support their hypotheses or allegations, the balance of probabilities is recharged in one way or another. From the foregoing it follows that the probability of the hypothesis or allegation of the party bearing the burden of proof, based on evidence 1, may be greater than or equal to the probability of the denial of the hypothesis or allegation of the counterparty, based on evidence 2, and vice versa.
From the above it follows that:
PB (Hparty/p1) ≥ PB (no-Hcounterparty / p2) or PB (no-Hcounterparty/p2) ≥ PB (Hparty/p1).
This grading of the support that pieces of evidence 1 and 2 give to the hypotheses or allegations of the parties is carried out in comparative terms; that is, they can only be compared and, therefore, said probabilities cannot be combined algebraically (Cohen, 2017; Schum, 2016).
Schematically, in so far as the parties produce and propose evidence favoring and disfavoring their hypotheses or allegations, the following balance is obtained:
PB (Hparty / p1) = 1 and PB (non-Hcounterparty / p1) = 0.
Therefore, PB (Hparty / p1)> PB (non-Hcounterparty / p1).
PB (Hparty / p1 and p2) = 0 and PB (non-Hcounterparty / p1 and p2) = 2.
PB (Hparty / p1 and p2) <PB (non-Hcounterparty / p1 and p2).
The evidentiary weight that evidence 1 gives to fact 1 is initially “little likely” and the evidentiary weight that evidence 2 gives to fact 1, later, is “likely”.14 This evidentiary conflict leaves fact 1 and the hypothesis or allegation of the party bearing the burden of proof without support. (Figure 8).
Table 3 shows the balance of probabilities for pieces of evidence 1 and 2, which show a pattern of contradiction (evidentiary dissonance). (Figure 5). (Tecuci, Schum et al., 2016).
Table 3 Baconian probabilities with fuzzy qualifiers for the calculation of the conjunct evidentiary weight of dissonant evidence
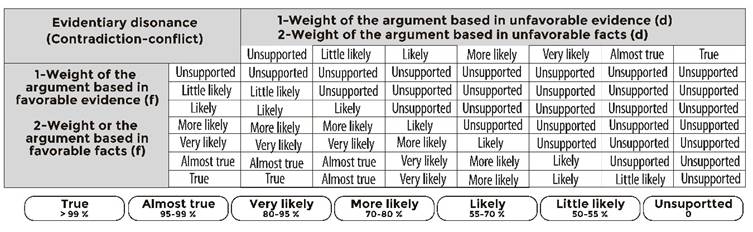
Source: own elaboration.
Figure 9 illustrates how the party with the burden of proof puts again in its favor, with evidence 3, the balance of probabilities related to its hypothesis or allegation.
Evidence 3 makes the Baconian probability of the hypothesis or allegation of the party bearing the burden of proof, [PB (Hparty)], greater than the probability of the denial of the hypothesis or allegation of the counterparty, based on said eviden- ce [PB (non-Hcounterparty)].15
PB (Hparty / p1) = 1 and PB (non-Hcounterparty / p1) = 0.
Therefore, PB (Hparty / p1)> PB (non-Hcounterparty / p1).
PB (Hparty / p1 and p2) = 0 and PB (non-Hcounterparty / p1 and p2) = 2.
PB (Hparty / p1 and p2) <PB (non-Hcounterparty / p1 and p2).
PB (Hparty / p1 and p2 and p3) = 3 and PB (non-Hcounterparty / p1 and p2 and p3) = 0.
PB (Hparty / p1 and p2 and p3)> PB (non-Hcounterparty / p1 and p2 and p3).
This balance of probabilities ends when one of the parties fails to try to prove a relevant fact that favors its hypothesis or allegation. If the party bringing the legal action meets the burden of proof to a certain degree or measure of probability, and the counterparty does not exceed or equal that degree or measure of probability, then the party bringing the legal action wins the legal process. But if it doesn’t, it loses.
Source: own elaboration
Figure 9 Production and proposition of evidence 3 by the party bearing the burden of proof
The party that wins the process will need to have demonstrated its argument, based on the standard of proof beyond all reasonable doubt, in the criminal trial, and on that of preponderant evidence, in the civil, administrative or labor trial.
The greater the evidentiary weight of the evidence taken into consideration, the greater the margin by which one of the parties exceeds the other.
PB (Hparty / p1) = 1 and PB (non-Hcounterparty / p1) = 0.
Therefore, PB (Hparty / p1)> PB (non-Hcounterparty / p1).
PB (Hparty / p1 and p2) = 0 and PB (non-Hcounterparty / p1 and p2) = 2.
PB (Hparty / p1 and p2) <PB (non-Hcounterparty / p1 and p2).
PB (Hparty / p1 and p2 and p3) = 3 and PB (non-Hcounterparty / p1 and p2 and p3) = 0.
PB (Hparty / p1 and p2 and p3)> PB (non-Hcounterparty / p1 and p2 and p3).
PB (Hparty / p1 and p2 and p3 and p4) = 4 and PB (non-Hcounterparty / p1 and p2
and p3 and p4) = 0.
PB (Hparty / p1 and p2 and p3 and p4)> PB (non-Hcounterparty / p1 and p2 and p3 and p4).
PB (Hparty / p1 and p2 and p3 and p4 and p5) = 5 and PB (non-Hcounterparty / p1 and p2 and p3 and p4 and p5) = 0.
PB (Hparty / p1 and p2 and p3 and p4 and p5)> PB (non-Hcounterparty / p1 and p2 and p3 and p4 and p5).
The evidentiary weight that evidence 4 gives to fact 2 is greater than 0 (“almost true” semantic differential criterion). Pieces of evidence 3 and 4 corroborate fact 2 with an evidentiary weight represented by the “almost true” semantic differential criterion, and converge on the hypothesis or allegation of the party bearing the burden of proof, making it “very likely”.16 (figure 5).
The evidentiary weight that evidence 5 gives to fact 3, which is unfavorable to the hypothesis or allegation of the party bearing the burden of proof, is greater than zero. The evidentiary weight that proof 5 gives to fact 3 is represented by the “more likely” semantic differential criterion.
However, given the low relevance of fact 3 (represented by the “likely” semantic differential criterion), this makes the evidentiary weight that evidence 5 gives to fact 3 to be represented by the “little likely” semantic differential criterion.17
Table 3, above, shows the balance of probabilities for the evidential weight of pieces of evidence 1, 2, 3 and 4 (represented by the “almost true” semantic differential criterion) in relation to the evidential weight of evidence 5 (represented by the “likely” semantic differential criterion), which exhibits a pattern of conflict (evidentiary dissonance). (figure 5). (Tecuci, Schum et al., 2016).
As said, this scheme ends when one of the parties fails to try to prove a relevant fact that favors its hypothesis or allegation.
2.2 Fuzzy logic
The expression “likely”, used by the expert system “Intelligent Judge”, although it is in common use, can have different meanings for different people. To handle the vagueness and imprecision in human evidentiary inferences in which the word “likely” is used, the “Intelligent Judge” expert system uses the fuzzy logic, proposed by Lofti Zadeh (Schum, 2016; Zadeh, 1983; Zadeh & Yager, 1987).
From this point of view, Zadeh proposes to use verbal expressions referring to the word “likely”, to accommodate numerical ranges of probability, such as those illustrated in figure 3 (Tecuci et al., 2016). The logic used here is not bivalent, it is multivalued, since the expression “likely” can take various values other than 0 and 1. The questions that were formulated in 1.1.1, 1.2.1 and 1.3.1 use the expression “likely” as a mechanism for accepting the premises that are included in the reasoning that is issued daily by judges and people in general (Cohen, 2021).
The premises and conclusions used and reached by the human judge, through such questions, are fuzzy in nature and, therefore, not as definitive as those used in conventional bivalent logic. The rules of experience, used in 1.1.1 and 1.2.1 to justify the values of relevance of facts and pertinence of evidence, are clear examples of the vagueness and imprecision that are present in the judicial decision. Modulators of the expression “likely” were used to justify such values of relevance and pertinence -which, as noted, are semantic differential criteria-, such as “more likely”, “very likely” or “little likely”, which, in themselves, are vague or fuzzy in nature.18
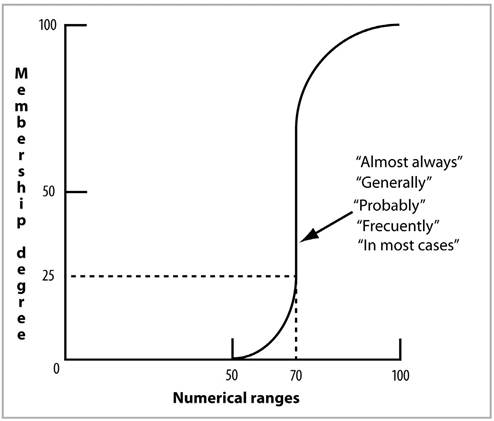
The expression “likely” is elastic in nature. Figure 10 illustrates a set of fuzzy expressions, such as “probably”, “generally”, “in most cases”, “almost always”, “frequently”, among others, that are specific to the rules of experience and are used as an intellectual device in the construction of inferences by people (Schum, 2016).
Figure 10 shows how no range less than 50 means “probably”, “generally”, “in most cases”, “almost always”, “frequently”. Membership in the fuzzy set “probably” corresponds to the numerical ranges between 50 and 100. The common sense of human beings is a collection of dispositions or events that we take “probably”, “usually”, “in most cases”, “almost always”, “frequently” as true (Schum, 2016).
The experience rules that make it possible to justify the values of relevance and pertinence that are assigned by the judge to the facts and the evidence, respectively, are affirmed in fuzzy terms (Tecuci et al., 2016).
The qualifiers chosen in figure 3 depend on the experience and knowledge that people have, who ultimately use them to justify the conclusions they reach. Figure 3 illustrates how such justifications can be established as verbal expressions of numerical ranges of probability, and not as unique numerical values of probability.
The work illustrated in figure 3 is a notable example of the scale developed by Tecuci, Schum, Marcu and Boicu, in the intelligence analyses, as specific probabilistic referents of the verbal justifications that account for the inquiries they carry out.
All lawyers know what is related to the standards of proof in criminal matters, such as “reasonable inference”, “probability of truth” and “beyond reasonable doubt”, among others, which are vague or in nature.
Similarly, Rule 375 of the Colombian Criminal Procedure Code, which prescribes what is related to the pertinence of the evidence (see footnote above, in 1.2.1), was established in fuzzy terms, since it uses the expression “more or less probable”.
2.3 Fuzzy Sets and Fuzzy Logic
The analysis proposed with the use of the “Intelligent Judge” expert system is an alternative method for grading the evidentiary weight in the made inferences, from the evidence to the facts and from the facts to the hypotheses or allegations that are raised by the party bearing the burden of proof in the judicial process.
For fuzzy logic, probability is a linguistic variable whose possible semantic representations and their equivalent numerical ranges are illustrated in figure 3 (Tecuci, Schum et al., 2016).
In 1.3.2 and 1.41 it was illustrated how, in the use of the “Intelligent Judge” expert system, combinations of these linguistic variables are used as predicates for the pertinence and credibility of evidence, as well as for the relevance of the facts and the evidentiary weight that evidence gives to them.19* This means that the judge can calmly say that he has a pertinent and credible evidence, or a relevant fact that has evidentiary weight, by means of the operations of conjunction, disjunction and negation, typical of the Baconian probabilities that were illustrated from 2.1, above.20
Depending on what the evidence is believed to mean, it is possible to justify, by means of the Baconian probability system illustrated in 2.1, the evidentiary weight that is assigned on the scale represented in figure 3. This scale accounts for the calibration of fuzzy judgments on the evidentiary weight of the evidence in the judicial process: the proposed mechanism to combine such fuzzy trials based on a set of evidence. It is our position to assert, even naively, that such an employed mechanism is quite plausible.
CONCLUSIONS
This article has presented a methodology, procedure, or algorithm and the “Intelligent Judge” expert system, which allows organizing the judge’s thinking regarding the motivation of the sentence that decides the judicial trial, from the evidence of the facts to the hypotheses or allegations that are considered in the judicial trial.
Said methodology, procedure, or algorithm involves a synergy between the knowledge, experience and evidentiary reasoning used by the judge and the speed and precision of artificial intelligence, through the use of the “Intelligent Judge” expert system to assist in the complex task of the assessment of the judicial proof.
Also, students and teachers can be assisted by the “Intelligent Judge” expert system in the elaboration of evidentiary inferences, which are quite useful in the subjects of Evidence Theory and Procedural Law. Practicing lawyers can now be better prepared to face judicial processes through the “Intelligent Judge” expert system, which assists them in predicting the judicial assessment that, based on the evidence, they can expect to be reflected in a judicial sentence.
Public prosecutors will have a support tool in the elaboration of inferences that allow them to quickly assess the alternative hypotheses that may be raised in the respective theory of the case and in the various stages of the evidentiary activity.
The probabilities system and the logic that are raised in the article, and used by the “Intelligent Judge” expert system, account for the transparent form of the evidentiary reasoning that can be used by the judge in the construction of the evidentiary arguments that serve as support for a rational evaluation of the evidence and, therefore, which make it the basis of a judicial decision in accordance, to a greater extent, with the justice value.
The operation of the “Intelligent Judge” expert system is illustrated by an example in the cybernetic link <https://youtu.be/B4XCG74YVSg>.