Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista Ciencias de la Salud
Print version ISSN 1692-7273On-line version ISSN 2145-4507
Rev. Cienc. Salud vol.4 suppl.1 Bogotá Oct. 2006
Descripción matemática con dimensiones fractales de células normales y con anormalidades citológicas de cuello uterino
Mathematical Description with Fractals Dimensions of Normal Cells and Cytological Abnormality's of Uterine Neck
Javier Rodríguez*, Signed Prieto**, Liliana Ortiz, Carolina Wiesner, Martha Díaz§, Catalina Correa
* MD. Médico Cirujano. Universidad Nacional. Director del Grupo Insight. E-mail: grupoinsight2025@yahoo.es
** Investigadora del Grupo Insight.
Investigadora Grupo Insight.
MD. Coordinadora grupo Planificación y Gestión Programas de Prevención. Instituto Nacional de Cancerología.
§ Psicopedagoga y Cito tecnóloga, especialista en Promoción en Salud y Desarrollo Humano. Grupo Planificación y Gestión Programas de Prevención. Instituto Nacional de Cancerología.
Psicóloga. Investigadora del Grupo Insight.
Recibido: 24 de agosto de 2006. Aceptado: 21 de septiembre de 2006.
Resumen
Introducción. La geometría fractal ha mostrado ser adecuada en la descripción matemática de objetos irregulares; esta medida se ha denominado dimensión fractal. La aplicación del análisis fractal para medir los contornos de las células normales así como aquellas que presentan algún tipo de anormalidad, ha mostrado la posibilidad de caracterización matemática de su irregularidad.
Objetivos. Medir, a partir de la geometría fractal células del epitelio escamoso de cuello uterino clasificadas como normales, atipias escamosas de significado indeterminado (ASC-US) y lesiones intraepiteliales escamosas de bajo grado (LEIBG), diagnosticadas mediante observación microscópica, en busca de mediciones matemáticas que las distingan.
Metodología. Este es un estudio exploratorio descriptivo en el que se calcularon las dimensiones fractales, con el método de box counting simplificado y convencional, de los contornos celular y nuclear de 13 células del epitelio escamoso de cuello uterino normales y con anormalidades como ASC-US y lesiones intraepiteliales de bajo grado (LEI BG), a partir de fotografías digitales de 7 células normales, 2 ASCUS y 4 LEI BG diagnosticadas con criterios citomorfológicos mediante observación microscópica convencional.
Resultados. Se desarrolló una medida cuantitativa, objetiva y reproducible del grado de irregularidad en las células del epitelio escamoso de cuello uterino identificadas microscópicamente como normales, ASC-US y LEI BG.
Conclusiones Se evidenció una organización fractal en la arquitectura celular normal, así como en células ASC-US y las lesiones intraepiteliales de bajo grado (LEI BG). No se encontraron diferencias entre los tipos celulares estudiados.
Palabras clave: Dimensión fractal, Cáncer de cuello uterino, Citología.
Abstract
Introduction. The fractal geometry has shown to be adapted in the mathematical description of irregular objects; this measurement has denominated fractal dimension. The application of the fractal analysis to measure the contours of the normal cells as well as those that present some type of abnormality, has shown the possibility of mathematical characterization of its irregularity.
Objectives. To measure, from the fractal geometry cells of the squamous epithelium of uterine neck classified like normal, atypical squamous cells of undetermined significance (ASC-US) and Low Grade Intraepitelial Lesion (L-SIL), diagnosed by means of microscopic observation, in search of mathematical measurements that distinguish them.
Methodology. This is an exploratory descriptive study in which the fractal dimensions were calculated, with the simplified and the conventional box counting method, of the cellular and nuclear contours of 13 normal and with abnormalities cells of the scaly epithelium of uterine neck like ASC-US and L-SIL, from digital photographies of 7 normal cells, 2 ASC-US and 4 L-SIL diagnosed with cytomorphologic criteria by means of microscopic conventional observation. Results. There developed a quantitative, objective and reproducible measurement of the degree of irregularity in the cells of the scaly epithelium of uterine neck identified microscopically like normal, ASCUS y LEI BG. Conclusions an fractal organization was demonstrated in the cellular normal architecture, as well as in cells ASC-US and the injuries intraepiteliales of low degree L-SIL. They did not find differences between the cellular studied types.
Key words: Fractal dimension, cancer of uterine neck, Cytology.
INTRODUCCIÓN
La geometría fractal se desarrolló a partir de la paradoja que surge al tratar de medir objetos irregulares con reglas euclidianas. Al intentar medir la longitud de la costa de Gran Bretaña se observó que si se disminuía la longitud de la regla, la longitud total de la costa aumentaba (1). En vista de esto Mandelbrot desarrolló una medida del grado de irregularidad de los objetos y la denominó dimensión fractal (2).
Las estructuras traqueobronquiales venosas y arteriales, las fibras de músculo cardiaco al igual que su sistema de conducción presentan una geometría irregular(3). Es por esto que la dimensión fractal ha sido considerada la medida más apropiada para medir las formas irregulares del cuerpo humano (4-7).
La geometría fractal ha sido utilizada para estudiar tumores malignos desde una perspectiva macroscópica. La geometría fractal permitió determinar un espectro de valores para las lesiones encontradas en cáncer de mucosa oral en la interface del tejido conectivo y epitelial (8). En muestras macroscópicas de cáncer de vejiga de alto y bajo grado, el cálculo de las dimensiones fractales, analizadas estadísticamente, permitió establecer los rangos de diferenciación (9). Así mismo las dimensiones fractales han permitido estudiar el efecto de andrógenos en el cambio de la fisiología y arquitectura tumoral (10).
Rodríguez (12) desarrolló una nueva metodología que permite medir matemáticamente tanto la totalidad de las arterias como sus partes componentes, las capas íntima, media y adventicia. A éstas las caracterizó con el concepto de Armonía Matemática Intrínseca (AMI) a partir de las dimensiones fractales, estableciendo diferencias de 1030 entre arterias sanas y arterias reestenosadas, logrando calcular la eficacia de las intervenciones moleculares en el proceso de reestenosis. Este mismo grupo (13), utilizando el concepto de variabilidad entre las dimensiones fractales de la ramificación coronaria izquierda (RCI), diferenció los pacientes con y sin enfermedad arterial oclusiva (EAO) severa.
Desde que el doctor Papanicolaou diseñó el sistema de clasificación citológica utilizado hasta el año de 1988, se ha intentado establecer una nomenclatura adecuada y homogénea para designar los hallazgos citomorfológicos en el cue llo uterino. En esta búsqueda se ha llegado hasta la nomenclatura propuesta por el sistema Bethesda 2001, que realizó aportes para la agrupación de una serie de anormalidades epiteliales que presentan dificultades debido a la diferenciación reproducible de algunos cambios sutiles presentes en las células al ser analizadas microscópicamente. Sin embargo, existen diferentes críticas a este sistema y aun no hay un consenso respecto a una clasificación específica y única a nivel mundial (14).
MATERIALES Y MÉTODOS
Este es un estudio exploratorio descriptivo en el que se tomaron 13 células de placas citológicas de cuello uterino del archivo personal de muestras de uno de los investigadores. Se seleccionaron 7 extendidos con células normales, 2 ASCUS y 4 con lesiones intraepiteliales de bajo grado (LEIBG) diagnosticadas con el sistema. Posteriormente las células se fotografiaron con cámara digital (Nikon) a través de microscopio (Nikon Eclipse å200) con aumento de 100X. Las fotografías se importaron a un editor de imágenes para su posterior análisis.
Para el análisis matemático se midieron las dimensiones fractales de los contornos de la membrana celular y de la membrana nuclear. Para esto se aplicó una simplificación del método de box Counting con sólo un par de rejillas, cuyos cuadros tenían lados de longitud de 2mm. y 32mm. y el método de box Counting tradicional con cinco rejillas. Por tratarse de medidas geométricas objetivas y reproducibles de cada célula, no es necesaria la aplicación de análisis estadísticos.
DEFINICIONES
Fractal: del latín fractus, interrumpido. Objeto irregular. Término que indica como adjetivo: irregularidad y como sustantivo: objeto irregular.
Dimensión fractal: medida numérica adimensional del grado de irregularidad de un fractal. Dimensión fractal de Box-Counting:
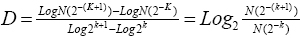
Donde: N: número de cuadros que contiene el contorno del objeto. K: grado de partición de la cuadrícula. D: dimensión fractal.
RESULTADOS
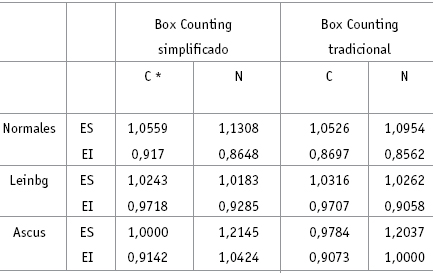
Las dimensiones fractales del contorno celular estuvieron entre 0,9142 y 1,0559 con el cálculo de las rejillas de 2mm. y 32mm. y entre 0,8697 y 1,0526 calculadas con las cinco rejillas. Para el contorno nuclear se encontró que las dimensiones fractales calculadas con el método simplificado de Box Counting estuvieron entre 0,8648 y 1,2145 y entre 0,8562 y 1,2037 calculadas con el método de Box Counting convencional (Tabla 1). Los valores de los extremos presentados en las dimensiones fractales, calculadas con los dos métodos, para células normales, ascus y leibg se presentan en la tabla 2.
Tabla 1. Dimensiones fractales de los contornos celular y nuclear. C: Dimensión fractal del citoplasma. N: Dimensión fractal del núcleo celular
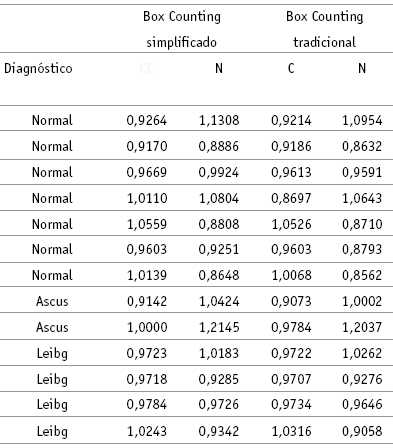
Tabla 2. Valores extremos de las dimensiones fractales de los contornos celular y nuclear. C: Dimensión fractal del citoplasma. N: Dimensión fractal del núcleo celular
DISCUSIÓN
Este es el primer trabajo a nivel mundial en el que se calculan dimensiones fractales de los contornos celular y nuclear, de forma objetiva y reproducible, de células clasificadas convencionalmente como normales, ASCUS y LEIBG, estableciendo una medida matemática que posiblemente pueda utilizarse en el futuro para caracterizaciones matemáticas de este tipo de células.
Esta metodología contribuye al estudio de la estructura irregular celular al proveer información cuantitativa, con resultados numéricos precisos que caracterizan matemáticamente estas células preneoplásicas con lo que se evidencia una organización geométrica fractal de las células.
Análisis fractales aplicados al cáncer han mostrado que son de gran utilidad en la reducción de falsos positivos en el diagnóstico de mamografías digitales (15), al igual que en la discriminación entre diferentes grados de lesión para tejido conectivo y epitelial en interfase de la mucosa oral(8). P Luzi et al.(9) analizaron con métodos estadísticos las dimensiones fractales de muestras de cáncer invasivo de vejiga y obtuvieron que el menor valor de la dimensión fractal se presentó en muestras de bajo grado de lesión. Baish y Jain(10, 11) con dimensiones fractales evaluaron el impacto del suministro de andrógenos en la evolución tumoral de ratones con tumores andrógeno dependientes. En este trabajo, se realizaron caracterizaciones celulares para diferentes estadios con cálculos matemáticos de sus Grados de irregularidad.
Las dimensiones fractales aisladas no son suficientes para comparar objetos irregulares. Para solucionar este problema Rodríguez y cols. desarrollaron el concepto de AMI, para realizar comparaciones entre las partes y la totalidad de arterias coronarias en un modelo experimental de reestenosis en porcinos(12). Este mismo grupo desarrolló una investigación(13) en Enfermedad Arterial oclusiva (EAO) severa donde con los conceptos de variabilidad y la diferencia neta de las dimensiones fractales diferenció pacientes con y sin EAO severa, y logró cálculos objetivos y reproducibles sin necesidad de tratamientos estadísticos. Metodologías como estas probablemente serán de gran utilidad en estudios posteriores en esta área de investigación.
La metodología simplificada de Box Counting propuesta constituye una medida independiente de todo tipo de análisis estadístico ya utilizada (12) y por tanto de linealizaciones y aproximaciones. Sin embargo, las dimensiones fractales de los contornos del núcleo y citoplasma no permiten diferenciar las irregularidades entre los tipos celulares calculados.
El sistema de Bethesda, del mismo modo que las nomenclaturas anteriores, está basado en observaciones cualitativas para determinar los grados de lesión, por ello es dependiente de la subjetividad y/o experiencia del especialista(14).
Esta investigación es una primera aproximación en el desarrollo de una metodología de diagnóstico clínico basada en caracterización matemática objetiva y reproducible.
LIMITACIONES
La dimensión fractal aislada no permite establecer comparaciones entre las células medidas, por lo que es necesario desarrollar medidas capaces de comparación entre los grados de irregularidad de estadios celulares sanos y cancerígenos.
CONCLUSIONES
La evaluación de los diferentes estadios celulares y sus contornos celulares y nucleares mostró una organización celular geométrica fractal. No se encontraron diferencias matemáticas entre las dimensiones fractales celulares de los grupos estudiados.
AGRADECIMIENTOS
Agradecemos al laboratorio de biología de la Universidad Nacional de Colombia sede Bogotá, en especial a la Dra. Argenis Bonilla, quienes nos facilitaron los equipos para obtener las fotografías de las placas citológicas.
REFERENCIAS
1. Mandelbrot B. ¿Cuánto mide la costa de Bretaña? En: Mandelbrot B. Los Objetos Fractales. Barcelona: Tusquets Eds. S.A.; 2000. p. 27-50. [ Links ]
2. Mandelbrot B. Introducción. En: Mandelbrot B. Los Objetos Fractales. Barcelona:Tusquets Eds. S.A.; 2000. p. 13- 26. [ Links ]
3. Goldberger AL, West BJ. Fractals in Physiology and Medicine. The Yale Journal of Biology 1987; 60: 421- 35. [ Links ]
4. Goldberger A, Rigney D, West B. Chaos and Fractals in Human Physiology. Sci Am 1990; 262: 42-49. [ Links ]
5. West BJ. Fractal Physiology and Chaos Medicine. London: World Scientific Publishing Co. 1990. [ Links ]
6. Goldberger AL. Non-linear Dynamics for Clinicians: chaos theory, fractals, and complexity at the bedside. Lancet. 1996; 347: 1312-4. [ Links ]
7. Goldberger AL. Fractal Dynamics in Physiology: Alterations with disease and angin. PNAS. 2002; 99: 2466-72. [ Links ]
8. Landini G, Rippin J. Fractal Dimensions of the Epithelial/Connective Tissue interfaces in Premalignant and Malignant Epithelial Lesions of the Floor of the Mouth. Anal. Quant Cytol Histol 1993, 15: 144-9. [ Links ]
9. Luzi P, Bianciardi G. Fractal Analysis in Human Pathology. Annals New York. Academy of sciences. p. 255-257. [ Links ]
10. Gazit Y, Baish JW, Safabakhsh N, Leunig M, Baxter LT, Jain RK. Fractal characteristics of tumor vascular architecture during tumor growth and regression. Microcirculation, 1997, 4: 395-402. [ Links ]
11. Baish JW, Jain RK. Fractals and Cancer. Cancer research 60, 3683- 3688, July 15, 2000. [ Links ]
12. Rodríguez J, Mariño M, Avilán, N, Echeverri D. Medidas fractales de arterias coronarias en un modelo experimental de reestenosis: Armonía matemática intrínseca de la estructura arterial. Rev. Col. Cardiol. 2002; 10 (2): 65-72. [ Links ]
13. Rodríguez J, Álvarez L, Mariño M, Avilán G, Prieto S, Casadiego E, et al. Variabilidad de la dimensión fractal del árbol coronario izquierdo en pacientes con enfermedad arterial oclusiva severa. Rev. Col. Cardiol. 2004; 11(4): 185-92. [ Links ]
14. Lacruz C. Nomenclatura de las lesions cervicales (de Papanicolau a Bethesda 2001). Rev. Esp. Patol. 2003; 36(1): 5-10. [ Links ]
15. Lefebvre F, Benali H. A Fractal Approach to the Segmentation of Microcalcifications in Digital Mammograms. Med Phys 1995; 22: 381-90. [ Links ]














