Transformación conforme para prescribir curvatura escalar a la esfera

Transformação conforme para prescrever curvatura escalar à esfera

Conformal transformation for prescribing scalar curvature on sphere

 

Claudia Granados-Pinzón¹ y Wilson Olaya-León²

¹ Magíster en Ciencias matemáticas, cigranad@uis.edu.co, profesora, Universidad Industrial de Santander, Bucaramanga-Colombia.

² Magíster en Ciencias matemáticas, wolaya@uis.edu.co, profesor, Universidad Industrial de Santander, Bucaramanga-Colombia.

(Recepción: 12-nov-2009. Modificación: 22-feb-2010. Aceptación: 22-feb-2010)

---

 

Resumen

Granados, en [1], ha demostrado la existencia de una familia de métricas conformes a la usual de la esfera unitaria con curvatura escalar n(n − 1). En el presente artículo se halla otra solución al problema de prescribir la curvatura escalar de Sⁿ por medio de una transformación conforme adecuada. Más aún, si se conociera una familia de soluciones al problema general, se obtendría otra familia de soluciones.

Palabras claves: métrica conforme, curvatura escalar, espacio de Hilbert, transformación conforme.

---

 

Resumo

Granados [1] mostrou a exisência de uma familia de métricas conformes à usual da esfera unitária com curvatura escalar n(n − 1). No presente artigo encontra se uma outra solução ao problema de prescrever a curvatura escalar da Sⁿ por meio de uma transformação conforme adecuada. Mais ainda, se conhêceramos uma familia de soluçoes ao problema geral, obteriamos uma familia de soluçoes.

Palavras chaves: métrica conforme, curvatura escalar, espaço de Hilbert, transformação conforme.

---

 

Abstract

In [1], Granados proved the existence of a whole family of conformal metrics to the Euclidean metric on Sⁿ having scalar curvature n(n −1). In this paper, we find another solution to the problem of prescribing scalar curvature on Sⁿ. Furthermore, if a family of solutions of the general problem is known, we get a new family of solutions.

Key words: conformal metric, scalar curvature, Hilbert space, conformal transformation.

---

 

Sea Sⁿ ={(x₁, x₂, . . . , x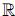_n+1) ∈ ⁿ⁺¹: 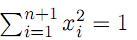} n ≥ 3, la esfera unitaria en 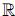ⁿ⁺¹ con la métrica usual g₀ = 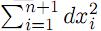. Sⁿ tiene entonces curvatura escalar constante igual a K₀ = n(n − 1) Si g es otra métrica riemanniana en Sⁿ , se dice que g es una deformación conforme de g₀ si y sólo si existe una función u suave positiva tal que g = 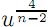g₀. Un problema clásico en geometría diferencial es determinar las funciones K definidas sobre Sⁿ para las cuales existe una métrica conforme a la métrica g₀ con curvatura escalar prescrita K en Sⁿ.

Dada la función K, la existencia de dicha g equivale a la existencia de una solución positiva suave u, definida en Sⁿ con valores reales, a la ecuación diferencial

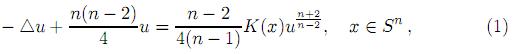
donde g = 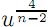g₀.

Si K(x) es constante, el problema es conocido como la conjetura de Yamabe, el cual fue estudiado por Yamabe (1960), Trüdinger (1968), Aubin (1976) y finalmente demostrado por Richard Shoen en 1984, ver [2, 3, 4]. Para una función de curvatura K(x) no constante el problema sigue sin resolver. Aunque son numerosos los intentos y los resultados concluyentes encontrados en relación al problema, en la actualidad sigue abierto ya que la gran dificultad en la solución de estos problemas es la falta de compacidad entre los encajamientos de los espacios de Sobolev asociados. El resultado más reciente ha sido presentado en el año 2001 por Wenxiong Chen and Congming Li [5], donde muestran una condición necesaria y suficiente para que el problema tenga solución.

En el caso particular, K(x) = K₀ = n(n − 1), todo se reduce a probar la existencia de una función positiva u que resuelva el problema

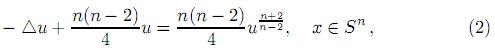
donde g = 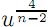g₀.

El teorema 1.1 garantiza la existencia de una familia de soluciones a (2) y, así, la existencia de una familia de métricas conformes a la usual en Sⁿ. Su demostración se puede ver en [1] ó [6] aunque el resultado fue presentado en [5] sin dar alguna sugerencia de su prueba.

Teorema 1.1. La ecuación diferencial no lineal (2) tiene infinitas soluciones

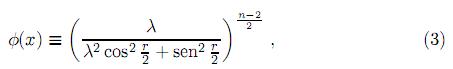
donde 0 ≤ r < π es un número real que depende de x y 0 < λ ≤ 1 es la variable que produce las infinitas soluciones de (2).

En la sección 2 se define una transformación conforme adecuada que permite hallar otra solución de (2).

 

2 Nota sobre la solución u ≡ 1

Considerando el espacio de Hilbert 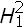(Sⁿ) = {u ∈ L²(Sⁿ) : ▽u ∈ L²(Sⁿ)}, cuya norma está dada por ||u||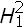_(Sⁿ)= ∫_Sⁿ(|▽u|² + 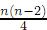dV), se define el conjunto S = {u ∈ 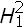(Sⁿ) : ||u||² = 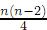|Sⁿ|, u > 0}, donde |Sⁿ| es el volumen de Sⁿ y tomando además que Sⁿ está centrada en e_n+1 = (0, . . . , 0, 1).

Siguiendo el bosquejo de la demostración del resultado más general que aparece en [5], se define a continuación la familia de transformaciones conformes T : S → S, dada por

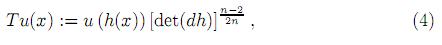
con h : Sⁿ → Sⁿ definida por

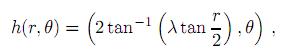
donde 0 < λ ≤ 1 y (r, θ) ∈ Sⁿ con 0 < r < π y θ ∈ Sⁿ⁻¹.

 

Lema 2.1.

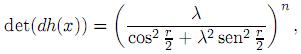
con 0 < λ ≤ 1.

Demostración. La derivada de h en el punto p es la función (dh)_p: T_pSⁿ→ T_pSⁿ definida por (dh)_p(v) = 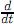h(α(t))|_t=0, donde α(t) es una curva en Sⁿ que satisface α(0) = p, α′(0) = v.

Para facilitar los cálculos, se extiendeha una función suave 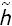: 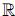ⁿ⁺¹→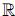ⁿ⁺¹. En consecuencia, se tiene que

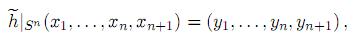
donde x₁ = θ₁sen r, . . . , x_n = θ_nsen r, x_n+1 = 1 − cos r, y₁ = θ₁ sen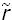,..., y_n = θ_n sen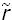, y_n+1 = 1 − cos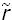, con 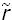= 2tan⁻¹ (λtan 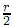) y (θ₁ ,...,θ_n) ∈ S^{n− 1} . Así, y_i = 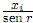sen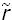, para 1 ≤ i ≤ n. De la expresión para 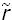se sigue que sen 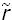= 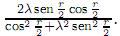Por consiguiente, y_i = 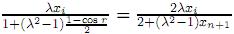, para i = 1,...,n. Además, y_n+1 = 1− cos 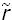= 1−

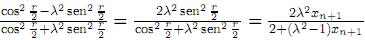. Entonces,

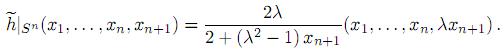
Por otra parte, la restricción de 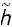a la esfera Sⁿ es simplemente h y, así, tiene rango n. De hecho, se tiene 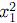+· · · + 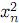+(x_n+1− 1)² = 1, lo cual permite despejar x_n+1 en función de las x_i, 1 ≤ i ≤ n. Por tanto, la última columna de la diferencial 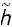tiene componentes nulas. De este modo, el determinante de dh es el subdeterminante de d 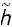correspondiente a las x_i, 1 ≤ i ≤ n. Es decir,

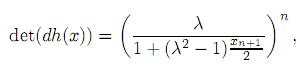
con 0 < λ ≤ 1. Usando coordenadas esféricas donde x_n+1 = 1 − cos r. Entonces,

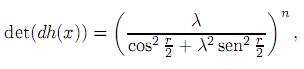
con 0 < λ ≤ 1.

El teorema 2.1 muestra la solución constante u ≡ 1 de (2) después de aplicar la transformación conforme (4) a la solución (3). Este resultado será generalizado en el teorema 3.1.

Teorema 2.1. Sean Φ y T definidos en (3) y (4) respectivamente, entonces

Demostración. Por (3) y el lema 2.1, se tiene que

 

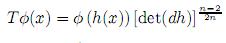
3 Transformación conforme y problema general

El método de transformación conforme ha sido utilizado para simplificar problemas que incluyen la ecuación de Laplace ya que ésta es invariante cuando se aplica la transformación [4, pág. 183].

Sean γ = 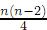τ = 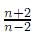y la función R(x) = 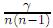K(x). Así, (1) se transforma en

El problema admite la siguiente interpretación variacional [2, 7]: multiplicando a (6) por u e integrando se tiene que

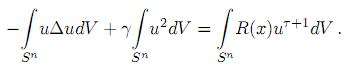
De la primera identidad de Green se sigue que

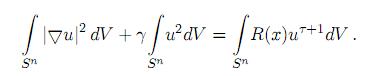
Se definen las funcionales

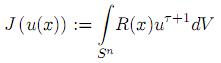
y

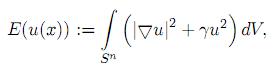
para u ∈ 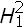(Sⁿ).

Se observa que ||u||² ≡ E(u), es decir, el conjunto S, definido en la sección 2, es simplemente S = {u ∈ 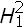(Sⁿ) : E(u) = γ|Sⁿ|, u ≥ 0}, donde|Sⁿ|es el volumen de S^n.

El lema 3.1, ver [5, pág. 66], muestra la relación entre los funcionales definidos anteriormente y la ecuación diferencial no lineal (6).

Lema 3.1. Un múltiplo escalar de un punto crítico de J en S es solución de (6).

A continuación se demuestra una importante propiedad de las funcionales J y E. Esta propiedad se conoce como invarianza conforme y permite encontrar, en el teorema 3.1, a otra familia de soluciones de (6).

Lema 3.2. J(Tu(x)) = J (u(x)) y E(Tu(x)) = E(u(x)), para u ∈ 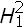(Sⁿ).

Demostración. Primero se verá que J (Tu(x)) = J(u(x)), para u ∈ 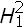(Sⁿ). En efecto, aplicando la transformación (4) y haciendo el cambio de variables y = h(x) se tiene que

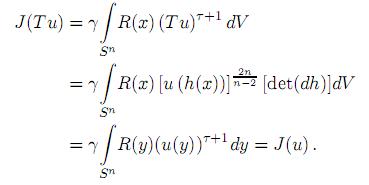
Ahora, se puede ver que E(Tu) = E(u), para u ∈ 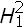(Sⁿ).

Por (4) y (5), se tiene que Φ ◦ h(x) = [det dh]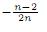. Además,

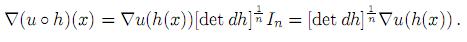
Luego,

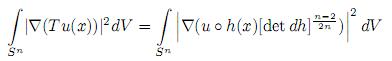
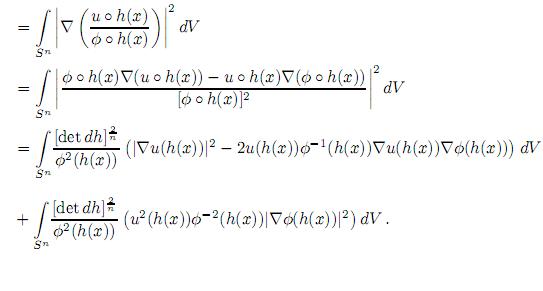
Por otro lado,

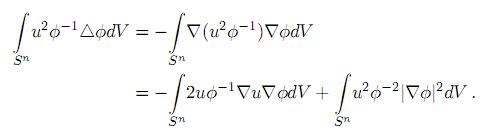
Así,

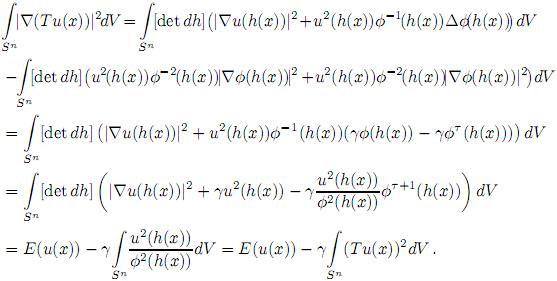
La tercera y cuarta igualdad se siguen de φ_q(h(x)) = (detdh)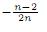 y T(u(x)) = u(h(x)) Φ⁻¹(h(x)), respectivamente.

En el teorema 3.1, que generaliza el resultado encontrado en el 2.1, muestra que si se conociera una familia de soluciones del problema más general de prescribir la curvatura escalar en Sⁿ , y utilizando la transformación conforme definida en (4), se obtendría otra familia de soluciones. Este resultado se presentó en [5] sin dar sugerencia de su demostración.

Teorema 3.1. Si u es solución de (6), entonces Tu también es una solución.

Demostración. De la definición de la derivada de Gâteaux y puesto que J(Tu) = J (u), se tiene que

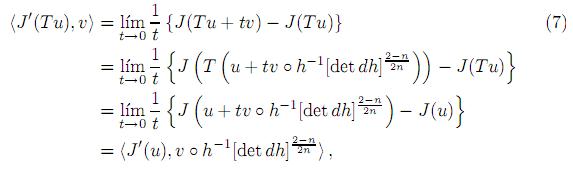
donde h⁻¹ es la inversa de h. Si u es solución de (6) entonces J′(u) = 0 y E(u) = γ|Sⁿ|. Así, por (7) y puesto que E(Tu) = E(u) teniendo que J′(Tu) = 0 y E(Tu) = γ|Sⁿ|. Lo cual implica que Tu es también una solución de (6).

 

4 Conclusiones

Se muestra una forma creativa de encontrar la solución trivial al problema de prescribir la curvatura escalar en la n-esfera con curvatura escalar n(n − 1). También se presenta una transformación conforme que puede ser útil en el problema de prescribir la curvatura escalar a la esfera. Es decir, si se conociera una familia de soluciones del problema general entonces utilizando dicha transformación se obtendría otra familia de soluciones.

El problema de prescribir la curvatura escalar a la esfera ha recibido gran atención en la literatura y varios autores han encontrado condiciones sobre K para la existencia de g, ver [1, 2, 5, 8, 9], pero en la actualidad sigue siendo un problema abierto.

 

Agradecimientos

Los autores expresan su agradecimiento a los árbitros de la revista por sus valiosas sugerencias y por supuesto a la Universidad Industrial de Santander por el apoyo prestado.

 

Referencias

1. C. Granados. Un caso particular del problema de prescribir la curvatura escalar en Sⁿ. Matemáticas: Enseñanza Universitaria, pISSN 0120-6788, eISSN 1900-043X, XV(1), 119-123 (2007). Referenciado en 47, 48, 49, 55         [ Links ]

2. T. Aubin. Some nonlinear problems in Riemannian Geometry, ISBN 3-540- 60752-8. Springer-Verlag, Berlin Heidelberg, 1998. Referenciado en 48, 52, 55        [ Links ]

3. R. Schoen. Conformal deformation of a Riemannian metric to constant scalar curvature. Journal of Differential Geometry, ISSN 0022-040X, 20(2), 479-495 (1984). Referenciado en 48        [ Links ]

4. R. Schoen, S. Yau. Lectures on Differential Geometry, Vol. 1, ISBN 1-57146- 012-8. International Press Publications, Boston, 1994. Referenciado en 48, 52        [ Links ]

5. W. Chen, C. Li. Prescribing scalar curvature on Sⁿ. Pacific Journal of Mathematics, ISSN 0030-8730, 199(1), 61-78 (2001). Referenciado en 49, 50, 52, 54, 55        [ Links ]

6. C. Granados. Tesis de maestría: Sobre la existencia de una métrica conforme a la métrica euclidiana en la n−esfera. Universidad del Valle, Santiago de Cali, 2005. Referenciado en 49        [ Links ]

7. LC. Evans. Partial differential equations, vol 19, ISBN 0-8218-0772-2. American Mathematical Society Providence, Rhode Island, 1998. Referenciado en 52        [ Links ]

8. W. Chen, W. Ding. Scalar curvatures on S². Transactions of the American Mathematical Society, eISSN 1088-6850, pISSN 0002-9947, 303(1), 365-382 (1987). Referenciado en 55        [ Links ]

9. R. Schoen, D. Zhang. Prescribed scalar curvature on the n−sphere. Calculus of variations and partial differential equations, ISSN 0944-2669, 4(1), 1-25 (1996). Referenciado en 55        [ Links ]