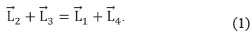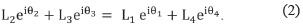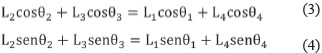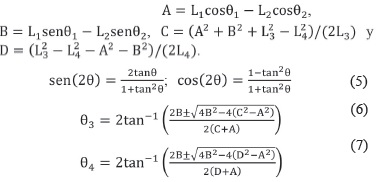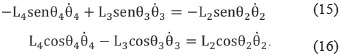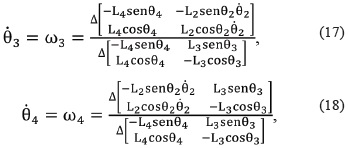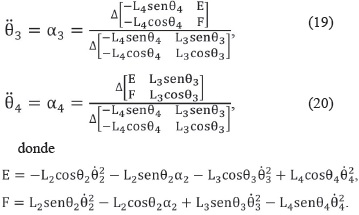Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Entre Ciencia e Ingeniería
Print version ISSN 1909-8367
Entre Ciencia e Ingenieria vol.10 no.20 Pereira July/Dec. 2016
APLICACION ANDROID PARA EL ESTUDIO DE MECANISMO PLANOS DE CUATRO BARRAS1
Android application for the study of four-link planar mechanism
Aplicativo Android para o estudo dos mecanismos planos de quatro barras
D. González*, E. Estrada** y J. Roldán***
1 Producto derivado del proyecto de investigación "Diseño de una aplicación para Android para el análisis cinemático de mecanismos planos de cuatro barras con fines didácticos". Presentado por el Grupo de Investigación DIMER, de la Universidad del Atlántico, Barranquilla (Colombia).
* D. González Miranda, Ingeniero Mecánico de la Universidad del Atlántico; Barranquilla, Colombia, email: dairo1021@hotmail.com.
** E. Estrada Gutiérrez, Ingeniero Mecánico de la Universidad del Atlántico; Barranquilla, Colombia, email: elegeleg@hotmail.com.
*** J. Roldán Mckinley, Ingeniero Mecánico de la Universidad del Atlántico, docente del Programa de Ingeniería Mecánica de la Universidad del Atlántico; Barranquilla, Colombia, email: javierroldan@mail.uniatlantico.edu.co.
Recibido Enero 20 de 2015 - Aceptado Mayo 30 de 2016
Resumen
Se presenta el desarrollo de una aplicación Android para el estudio cinemático del mecanismo plano de cuatro barras con juntas de revoluta. Se requiere del estudio completo de cinemática de posición, velocidad y aceleración, tomando como entrada uno de los eslabones con junta anclada al bastidor. Además de calcular la posición, velocidad y aceleración de los elementos, se clasifica el tipo de mecanismo de acuerdo con la ley de Grashof. La retroalimentación, por parte de estudiantes que han cursado asignaturas relacionadas con la temática de la aplicación, fue recibida a través de una encuesta, lo cual permitió cuantificar el desempeño de la herramienta. Los resultados obtenidos luego de usar la aplicación fueron validados contra resultados de libros de texto y de otras herramientas computacionales.
Palabras clave: Android app, mecanismo cuatro barras, diseño de mecanismos y máquinas, educación de la ingeniería.
Abstract
The development of an Android app for the study of four-link mechanism with the same number of revolute joints is presented. The created app requires a complete study of planar kinematics: position, velocity and acceleration, setting one of the grounded joints as the input. Besides calculating the position, velocity and acceleration of the moving elements, the application also classifies the mechanism, according to the Grashof Law. The feedback received from the students that have already taken courses related to the application topic was used in order to quantify the app performance. The results of the app calculations were validated through comparison against results of widely known textbook problems, and with similar computer running tools as well.
Key words: Android app, four-link mechanism, mechanism and machine design, engineering education.
Resumo
Se apresenta o desenvolvimento de um aplicativo Android para o estudo cinemático do mecanismo plano de quatro barras com juntas de revoluta. Requer-se do estudo completo de cinemática de posição, velocidade e aceleração, tomando como entrada um dos elos com junta ancorada ao bastidor. Além de calcular a posição, velocidade e aceleração dos elementos, se classifica o tipo de mecanismo de acordo com a lei de Grashof. A retroalimentação, por parte de estudantes que cursaram matérias relacionadas com a temática do aplicativo, foi recebida através de uma pesquisa, que permitiu quantificar o desempenho da ferramenta. Os resultados obtidos logo de usar a aplicação foram validados contra resultados de livros de texto e de outras ferramentas computacionais.
Palavras chave: Android app, mecanismo quatro barras, desenho de mecanismos e máquinas, educação da engenharia.
I. INTRODUCCIÓN
La Teoría de Mecanismos y Máquinas es una ciencia aplicada que relaciona, mediante el análisis cinemático, la geometría y los movimientos de las piezas [1]. Uno de los casos de estudio clásico dentro de esta área es el mecanismo de cuatro barras, debido a su gran uso por la facilidad de aplicación, este mecanismo es usado en sistemas de equipaje de vehículos comerciales [2] y en desarrollo de modelos dinámicos para la ingeniería biomédica [3]; además de ser objeto de estudio para generación de trayectoria [4], [5], en los cuales se trata de determinar la configuración apta de un mecanismo que permita que un punto del mismo describa una serie de coordenadas llamadas puntos de precisión [5].
Teniendo en cuenta la importancia del estudio del mecanismo de cuatro barras dentro de la Ingeniería Mecánica, se justifican los esfuerzos que se realicen para mejorar su proceso de enseñanza-aprendizaje. Para el análisis cinemático del mecanismo de cuatro barras se han desarrollado diversas herramientas como los software [6][9], que le permiten al estudiante corroborar los resultados de los problemas, al tiempo que facilita la labor del docente haciendo su clase más interactiva y pedagógica. Dentro de estos paquetes especializados se destacan el software provisto por R. Norton [7], completo desde el punto de vista numérico, con buena visualización gráfica, pero limitada interacción. Así mismo, se resalta el software desarrollado en GUIDE de Matlab [10], que permite la visualización completa de un ciclo del mecanismo, e interactividad con el usuario mediante modificación gráfica de longitudes de eslabones a través del teclado y del mouse del computador.
La importancia del estudio del mecanismo de cuatro barras también ha conllevado al desarrollo de aplicaciones para celulares Smartphone [11], [12] en sistema operativo Android, diseñadas con el fin de afianzar los conocimientos de los estudiantes en las asignaturas relacionadas. Algunas de las aplicaciones disponibles presentan interactividad limitada o fueron desarrolladas en lenguajes diferentes al español. Este trabajo plantea una continuación del trabajo desarrollado en la referencia [10] a ser desarrollado ahora en plataforma Android, aprovechando la similitud de la interactividad de su programa y el uso de los celulares táctiles y las tablets, que sugiere una fácil manera de cambiar las longitudes de los elementos de un mecanismo, haciendo los mismos movimientos que realiza el usuario del celular o la tablet para aumentar el tamaño del texto o la fotografía (zoom). Se inicia con el análisis cinemático del mecanismo de cuatro barras, luego se crean los algoritmos a ser programados y ejecutados en Android y así generar una aplicación que genere resultados que puedan ser corroborados con bibliografía y herramientas computacionales existentes. Se pretende proponer una innovación para el modelo de aprendizaje mediante el uso de una tecnología de uso masivo, de fácil acceso y manejo para cualquier estudiante [13].
II. FUNDAMENTOS DEL MECANISMO DE CUATRO BARRAS
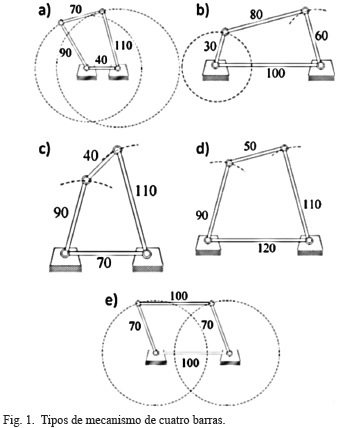
Se define un mecanismo de cuatro barras con cuatro juntas de rotación (revoluta) como aquel formado por cuatro elementos o eslabones, cualquiera de los mostrados en la Fig. 1, con un elemento que no rota llamado bastidor o tierra. Definiendo la inversión cinemática del mecanismo como el cambio del bastidor, se puede predecir el comportamiento de rotación del eslabonamiento de cuatro barras haciendo uso de la condición de Grashof, basándose en la longitud de sus eslabones S, L, P y Q; siendo S: longitud del eslabón más corto, L: longitud del eslabón más largo, P y Q: longitudes de los eslabones restantes. Con el fin que los cuatro eslabones se ensamblen y el mecanismo se pueda mover, la longitud del eslabón más largo L debe ser menor que la suma de las longitudes los restantes, es decir L < S+P+Q. Si se tiene que L = S+P+Q habrá eslabonamiento pero el mecanismo no podrá moverse, este es llamado el criterio de Grubler [18].
Un mecanismo cuatro barras es tipo Grashof si se cumple que S+L ≤ P+Q, y al menos uno de sus eslabones describirá una revolución completa, llamada cadena cinemática Clase I. Si el mecanismo de cuatro barras no cumple la desigualdad entonces, es No Grashof y ningún eslabón podrá dar una revolución completa, dándose la cadena cinemática Clase II. También puede darse que S+L = P+Q para el caso especial de Grashof Clase III. Las inversiones en este estudio se relacionan con el eslabón más corto del mecanismo.
A. Mecanismo de cuatro barras clase I
Si se tiene el eslabón más corto del mecanismo de cuatro barras designado como el marco fijo, Fig. 1.a, se obtiene un mecanismo doble-manivela; los tres eslabones móviles describen revoluciones completas. Si el eslabón más corto del mecanismo es adyacente a la bancada, Fig. 1.b, se obtiene un mecanismo manivela-balancín, el eslabón más corto describirá una revolución completa y el otro eslabón oscilará pivotado a la bancada. Si el eslabón más corto es el opuesto a la bancada, Fig. 1.c, se obtiene un mecanismo doble-balancín y los eslabones pivotados a la bancada oscilarán mientras el acoplador realizará una revolución completa.
B. Mecanismo de cuatro barras clase II
En los mecanismos de cuatro barras Clase II, todas las inversiones serán balancines triples, donde ningún eslabón podrá realizar una revolución completa. La Fig. 1.d presenta un ejemplo de un mecanismo triple balancín.
C. Mecanismo de cuatro barras clase III
Los mecanismos planos de cuatro barras Clase III son caso especial de Grashof, Fig. 1.e. Todas las inversiones son doble-manivelas o manivela-balancín. Tendrán dos puntos de cambio por revolución de la manivela de entrada, donde todos los eslabones se vuelven colineales, y el comportamiento de salida se indetermina, teniendo un mecanismo impredecible. Su movimiento debe ser limitado intencionalmente para evitar que alcance los puntos de cambio.
D. Clasificación completa de mecanismos de cuatro barras
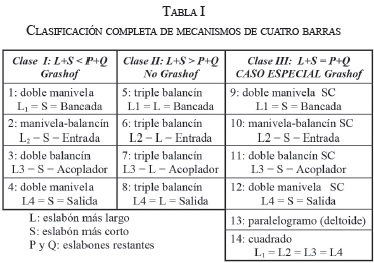
La clasificación completa de los mecanismos de cuatro barras se muestra en la Tabla I, basada en un sistema creado por Barker [19] que predice el movimiento del mecanismo.
E. Análisis de posición del mecanismo de cuatro barras
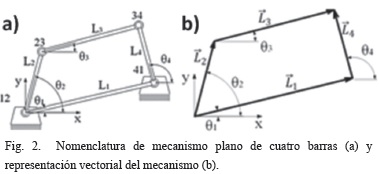
Considere el mecanismo de cuatro barras que se presenta en la Fig. 2.a, con longitudes de los eslabones, L1, L2, L3, y L4, y el ángulo de posición correspondiente a cada elemento θ1, θ2, θ3 y θ4, respectivamente. El análisis de posición del mecanismo se inicia representando su lazo vectorial, tal como se muestra en la Fig. 2.b. Los eslabones se representan como vectores de posición con cola ubicada en la junta en la cual se define el ángulo de posición del elemento. Los ángulos de posición θ1, θ2, θ3 y θ4, de los elementos 1, 2, 3 y 4 se definen, respectivamente, en las juntas 12, 23, 34 y 41, en sentido antihorario a partir del semieje positivo x, tal como se muestra en la Fig. 2.b. Las magnitudes de los vectores son las longitudes de los eslabones ya conocidas. La entrada del mecanismo será el ángulo θ1 ya que es un mecanismo de un grado de libertad (GDL), y el ángulo del eslabón fijo es θ1.
Por lo anterior, se requiere encontrar los ángulos θ3 y θ4.
Con base en el lazo de la Fig. 2.b, la ecuación vectorial es
Utilizando la notación de Euler, (1) se reescribe como
La expansión de (2) en componentes real e imaginaria permite establecer (3) y (4).
La solución de (3) y (4) mediante el uso de las identidades de la tangente del ángulo medio presentadas en (5), permite hallar las expresiones para los ángulos θ3 y θ4, presentadas en (6) y (7), respectivamente, donde
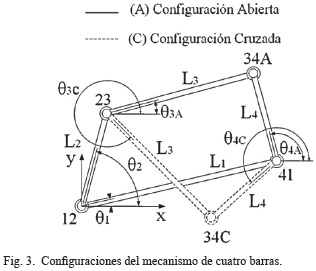
F. Configuraciones del mecanismo de cuatro barras
Las ecuaciones (6) y (7) tienen dos soluciones obtenidas a partir de las condiciones ± antes del radical. Estas soluciones, son de tres tipos: reales e iguales, reales y desiguales, complejas conjugadas. Si el discriminante bajo el radical es negativo, la solución es compleja conjugada, lo cual significa que las longitudes de los eslabones elegidas no son capaces de conectarse con el valor elegido del ángulo de entrada θ2. Esto puede ocurrir cuando las longitudes de los eslabones no establecen una conexión en cualquier posición; en un mecanismo de no Grashof, cuando el ángulo de entrada queda más allá de la posición límite de agarrotamiento. No existe entonces ninguna solución real con ese valor del ángulo de entrada θ2 Excepto en esta situación, la solución será real y desigual, lo cual significa que existen dos valores deθ3 y θ4 que corresponden a un valor de θ2. Éstas se conocen como configuraciones cruzada y abierta, representadas en la Fig. 3. En el mecanismo de cuatro barras, las soluciones positivas de θ3 y θ4 corresponden a la configuración abierta, y las soluciones negativas de θ3 y θ4 a la configuración cruzada.
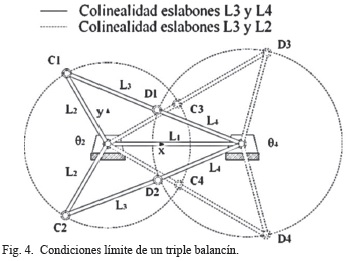
G. Posición de agarrotamiento en mecanismos No Grashof
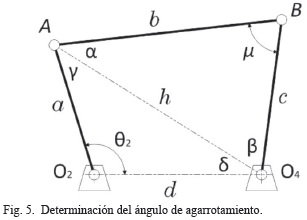
Los mecanismos de cuatro barras de tipo no Grashof poseen posiciones límites o posiciones de agarrotamiento, que ocurren cuando el eslabón acoplador presenta colinealidad con uno de sus dos eslabones adyacentes, Fig.4. En estas posiciones el mecanismo presentará trabamiento evitando que este continúe en movimiento. Estas posiciones de agarrotamiento se calculan aplicando la ley del coseno en el esquema de la Fig. 5, para obtener el ángulo de transmisión µ en función de las longitudes de los eslabones y los ángulos del eslabón de entrada θ2.
Con el fin de encontrar los valores máximo y mínimo de θ2 se deriva (11), derivando θ2 con respecto a µ e igualando a cero para obtener (12), de donde se determina que los valores límites de θ2 son µ igual a cero o 180° como se deduce en (13), para obtener finalmente el ángulo límite o de agarrotamiento, θ2L, presentado en (14).
H. Análisis de velocidad y aceleración
El análisis de velocidad parte de (3) y (5), estas ecuaciones son derivadas con respecto al tiempo, con θ1 =0 se obtiene
Aplicando la regla de Cramer se resuelve el sistema de ecuaciones (15) y (16) hallando θ3 y θ4, respectivamente:
donde Δ denota el determinante de la matriz.
Para el análisis de aceleración, se derivan (15) y (16), sabiendo que θ4=0 resuelve el sistema 2x2 y se hallan θ3 y θ4, presentadas en (19) y (20), respectivamente:
El conocimiento del modelado de la cinemática del mecanismo permite el diseño de las funciones de cálculo y de los algoritmos para la aplicación.
III. METODOLOGÍA EN EL DISEÑO DE LA APLICACIÓN
Android es un sistema operativo y una plataforma software móvil basado en Linux y de uso para teléfonos móviles y tablets, que permite programar en los entornos de trabajos de Java. Una aplicación en Android es un programa creado para la interactividad del usuario en su celular o tablet, en el cual se puede encontrar, intercambiar, almacenar información, o tener a la mano una herramienta que facilite cualquier actividad de la vida cotidiana; esta tiene componentes gráficos como campos de textos, botones, menús, imágenes, gráficas, etc.
Para la creación de aplicaciones en Android existen varios entornos de trabajos de programación como Eclipse, ver Fig.6, AndroidStudio, o en línea con MIT App Inventor. Además se necesitan los Kits de desarrollo de software para Android-SDK el cual contiene una máquina virtual para simular la aplicación, y el Java SE Development Kit-JDK; en el caso de Eclipse también el Plugin Android Development Tools-ADT.
Las partes importantes del diseño de una aplicación en Android son el Manifiesto, las actividades y los layouts. El manifiesto es donde se definen las características generales de la aplicación como el nombre, las versiones de instalación, los paquetes de actualización, los permisos para la instalación, y la relación entre las actividades y los layouts. Las actividades son tipo de archivo Java, la cual realiza la funcionalidad de la aplicación y que van en relación con la interacción con el usuario; y los layouts de tipo de archivos XML definen las vistas o ventanas donde se posicionan todos los elementos como textos, cajas de textos, botones etc.
La metodología empleada para el desarrollo de la aplicación para Android fue la de "marco de trabajo" (Framework) usado para estructurar, planificar y controlar el proceso de desarrollo en sistemas de información. Se acogió un enfoque de modelo en cascada o proceso secuencial de desarrollo en el que los pasos son vistos hacia abajo a través de las fases de análisis de las necesidades, el diseño, implantación, validación e integración.
El primer paso para el desarrollo de la aplicación fue la investigación, recopilación y estudio de las teorías acerca del mecanismo plano de cuatro barras, su principio de funcionamiento, su análisis de posición, velocidad y aceleración, con el fin de generar los algoritmos usados para cada etapa de análisis. Simultáneamente, se investigó acerca del sistema operativo Android, la elaboración de programas y plataformas para crear aplicaciones y el respectivo proceso de legalización. Se procedió a capacitaciones sobre diseños de aplicaciones para Android, con énfasis en animaciones.
Se continuó definiendo todos los procesos o funciones que conformaron la aplicación, creando una lista de pasos secuenciales, desde el ingreso de datos hasta la simulación de los mecanismos, luego se definió el diseño visual de la aplicación, ingreso de datos, configuraciones de botones, textos, cajas de ingresos de datos, etc. A partir de los datos ingresados, la aplicación valida el mecanismo, procediendo a clasificarlo, realiza el análisis cinemático y simula el movimiento del mecanismo. Se desarrolla en la aplicación una función que permite la edición de las longitudes de los eslabones usando el efecto táctil de la pantalla haciendo deslizamiento con los dedos, y en tiempo real muestra la clasificación del mecanismo creado. Por último se socializó la aplicación a todos los estudiantes de Teoría de Mecanismo y Máquinas de la Universidad, para revisar su diseño y recibir sugerencias para la mejora de los aspectos diseñados [13]-[17].
IV. LOGARITMOS UTILIZADOS EN LA APLICACIÓN
Se realizan los diagramas de flujos como soporte y simplificación para la representación de la secuencia y los pasos que la aplicación toma en cada una de sus funciones.
A. Función "calcular"
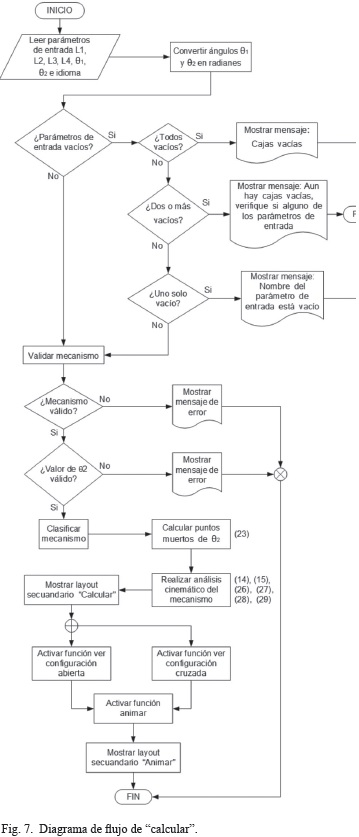
Cuando el botón calcular es pulsado en la aplicación, se verifica que los parámetros de entrada corresponden a un mecanismo válido; luego clasifica y realiza el análisis cinemático, y los muestra en el layout secundario "Calcular" y activa la función "ver" la cual permite visualizar el mecanismo en cualquiera de sus configuraciones, Fig. 7.
B. Función "validar mecanismo"
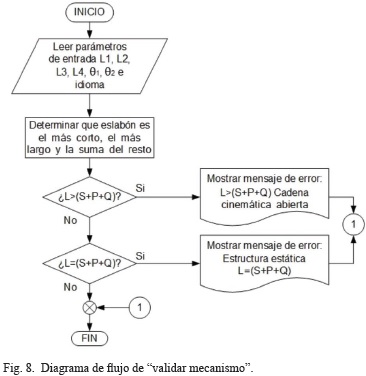
Esta función aplica el criterio de Grübler para determinar si los parámetros de entrada corresponden a un mecanismo válido, de lo contrario, mostrará un mensaje describiendo el error y una posible solución, Fig. 8.
C. Función "validar O2"
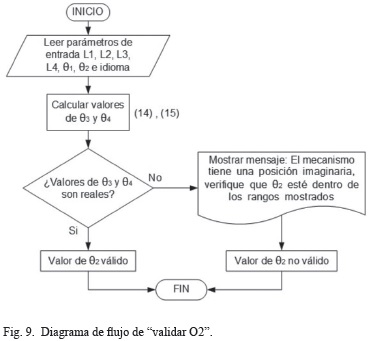
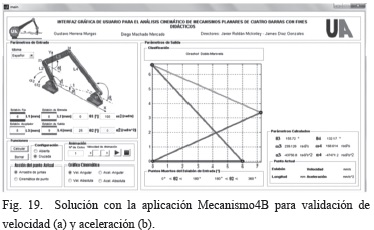
Esta función verifica si el mecanismo ingresado corresponde a una solución real o imaginaria, en el caso que la solución sea imaginaria se mostrará un mensaje describiendo el error y su solución, Fig. 9.
V. DESCRIPCIÓN DE LA APLICACIÓN
La aplicación para Android para el análisis cinemático de mecanismos planos de cuatro barras con fines didácticos tiene como nombre "Mecanismo4B", fue desarrollada en el entorno de trabajo Eclipse (IDE) con sus respectivas herramientas para el desarrollo de Android: ADT-Plugin, y los software de Android SDK, Java Development Kit (JDK). Está conformada por 5 layouts o distribuciones, uno principal donde se encuentran los parámetros de entrada, y cuatro secundarios: Parámetros de salida y cálculos, gráfico del mecanismo, Animación y 2D.
A. Ícono de la aplicación Mecanismo 4B
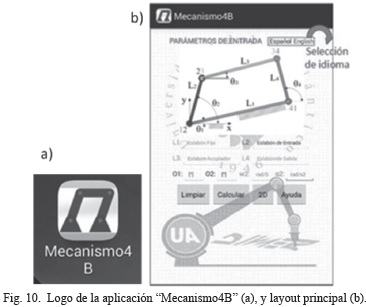
La aplicación se identificará en cualquier dispositivo Android al instalarlo, mediante el logo de la Fig. 10.a.
B. Layout principal "parámetros de entrada"
El layout principal contiene el nombre de la aplicación en la parte superior; como fondo, el escudo de la Universidad del Atlántico y el logo del grupo de investigación DIMER, como se muestra en la Fig. 10.b. En los parámetros de entrada, consta de una imagen que representa el mecanismo de cuatro barras y muestra la nomenclatura para identificar los eslabones y ángulos. En la parte inferior contiene textos y cajas de texto para ingresar los valores de longitud de eslabones y ángulos. En su parte final se encuentran los botones de las funciones Limpiar, Calcular, 2D y Ayuda.
C. Layout para función "ayuda"
El layout de ayuda, Fig. 11.a, aparece al presionar el botón "ayuda"; muestra una descripción de la aplicación y una serie de pasos que indican como usarla.
D. Layout secundario para función "calcular"
Este layout, Fig. 11.b, se hará visible cuando se presione el botón "calcular", en él se muestran los parámetros de entrada en los cuales se realizaron los cálculos, debajo la clasificación del mecanismo, puntos muertos del ángulo θ2 y por último los parámetros calculados, donde muestra la cinemática del mecanismo en las dos configuraciones de los mecanismos de cuatro barras (Abierta y Cruzada).
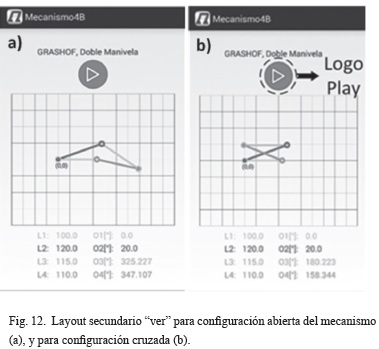
E. Layout secundario para función "ver"
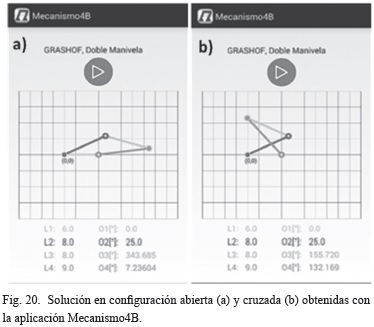
Cuando la aplicación realiza el cálculo cinemático del mecanismo tiene la opción de visualizar sus dos posibles configuraciones, Fig. 12.a y 12.b. Al presionar el botón "ver" se mostrará el mecanismo según la solución elegida.
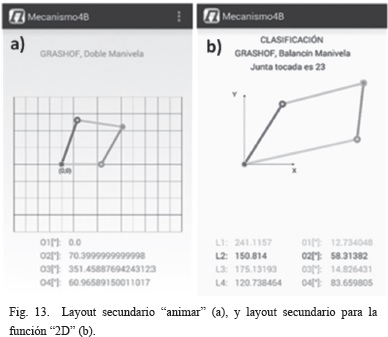
F. Layout secundario para función "animar"
Este layout se visualizará cuando se presione el boton "play", Fig. 12.b, y se reproducirá la animación del mecanismo, además de mostrar su clasificación y la variación de los parámetros calculados, Fig. 13.a.
G. Layout secundario para función "2D"
Este layout se mostrará al presionar el botón 2D en el layout principal de la Fig. 10.b, esta es parte interactiva de la aplicación dado que al iniciarse mostrará un mecanismo predeterminado que depende de la resolución del Smartphone, el cual puede ser editado con los dedos al desplazar las juntas de revoluta. Así mismo, en tiempo real mostrará la clasificación del mecanismo dibujado, la junta de revoluta tocada y las longitudes y ángulos de los eslabones, Fig. 13.b.
H. Validación por datos de entrada inapropiados
La aplicación está diseñada para evitar que el usuario ingrese valores inapropiados en los parámetros de entrada como números negativos, letras y símbolos, por lo cual el teclado de la aplicación solo mostrará números y no permitirá el ingreso del signo negativo, Fig. 14.
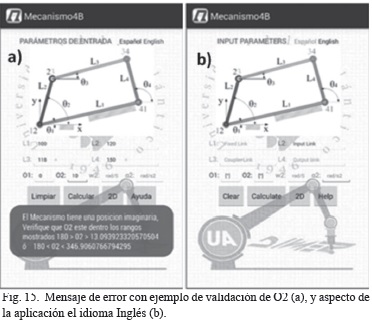
I. Mensaje de error
La aplicación cuenta con mensajes para describir el posible error que se haya cometido al ingresar un parámetro de entrada, o en la verificación de los mismos al validar un mecanismo, además de mostrar la solución a dicho error, ejemplo Fig. 15.a.
J. Relacion color-eslabón
La aplicación cuenta con una relación de color-eslabón para una fácil identificación visual y asociación de eslabones. Los colores de la caja de la longitud del eslabón en los parámetros de entrada concuerdan con los colores del eslabón dibujado en el plano, Figs. 10.b, 12, 13, 14.
K. Idioma de la aplicación
La aplicación cuenta en su layout principal con la opción de establecer el idioma: español o inglés, Fig. 10.b. La Fig. 15.b muestra el layout de la aplicación en el idioma inglés. Todas las funciones "Clear", "Calculate", "2D" y "Help", presentan la misma funcionalidad que en la opción de idioma español.
L. Resumen de la aplicación
En total se desarrollaron nueve funciones, creadas en la plataforma Eclipse con los kit de desarrollo software para Android (SDK), el Java SE Development Kit (JDK), el Plugin Android Development Tools (ADT), instaladas inicialmente en un dispositivo Huawei G630-U251 para pruebas preliminares de validación y encuesta.
VI. RESULTADOS
Para comprobar las soluciones dadas por la aplicación, los resultados a problemas tipo de un curso de Teoría de Mecanismos obtenidos con la aplicación desarrollada se comparan con los resultados de libros de texto y otra herramienta disponible, tal como una interfaz gráfica de usuario-GUI desarrollada en GUIDE de Matlab [10].
A. Validación de análisis de posición
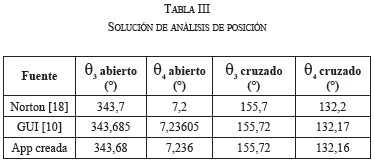
Se comparan los resultados de un ejercicio propuesto en la referencia de autor R. Norton [18] para análisis de posición de un mecanismo de 4 barras, con datos de entrada mostrados en la Tabla II. La Tabla III presenta los resultados de la solución obtenida por el mismo autor; los resultados obtenidos utilizando la interfaz de la referencia [10] y los arrojados por la aplicación desarrollada. Se obtuvieron los mismos resultados en cada caso.
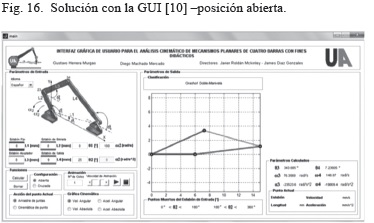
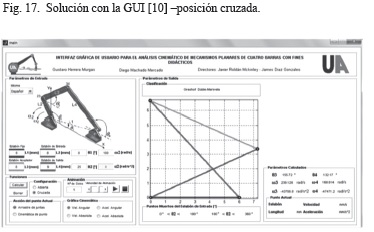
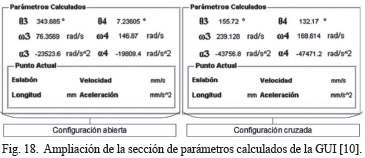
Ahora se compararán las salidas gráficas de la aplicación con las arrojadas por la GUI de la referencia [10]. Los resultados de θ3, θ4, y las gráficas de representación del mecanismo obtenidas con la GUI de [10] se muestran en las Figs. 16, 17 y 18. Las Figs. 20 y 21 muestran los resultados obtenidos con la aplicación. Al comparar los resultados numéricos para la posición de las Figs. 18 y 19, se observa que son los mismos. En cuanto a la comparación gráfica, las Figs. 16 y 17 concuerdan con las soluciones abierta y cruzada de las Figs. 20.a y 20.b, respectivamente. Los valores α3 y α4 de la GUI [10] son diferentes debido que esta trabaja con velocidad ω2 constante.
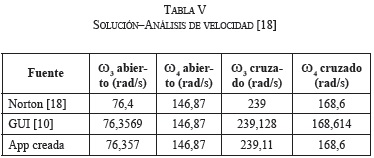
B. Validación de análisis de velocidad
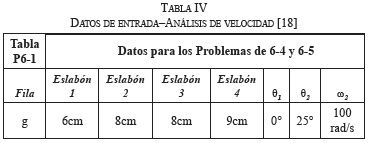
De la referencia [18] se realiza el problema para análisis de velocidad con los datos de entrada con velocidad constante de la Tabla IV, y los resultados reportados por el mismo autor en la Tabla V, en la cual también se presentan los resultados obtenidos utilizando la aplicación creada, Fig. 19.a y los obtenidos con la interfaz de la referencia [10], Fig. 18. Se obtuvieron prácticamente los mismos resultados.
C. Validación de análisis de aceleración
E. Encuesta de retroalimentación
Con el propósito de tener una opinión de los usuarios y mejorar la aplicación Android "Mecanismo4B", la misma se socializó entre los estudiantes de la asignatura de "Teoría de Mecanismos y Máquinas" de la Universidad del Atlántico, 2015-1. Posteriormente, la aplicación fue socializada a pequeños grupos de estudiantes activos del programa que ya habían cursado tal asignatura, para un total de 40 encuestados. La encuesta tomada se muestra en la Tabla IX [20]. Entre los aspectos a calificar en la encuesta se encuentran: funcionalidad del sistema, manipulación de la aplicación y diseño de la aplicación como lo sugiere. Cada aspecto contiene varias preguntas que se califican con un valor en una escala de 1 a 5, siendo 1 el nivel mínimo y 5 el mayor nivel de importancia.
Los resultados obtenidos son satisfactorios, muestran una gran aceptación de cada aspecto e ítem evaluado, Tabla IX, por parte de los estudiantes. Los resultados sugieren que la manipulación de la aplicación es uno de los aspectos a resaltar. La importancia de estos resultados radica en su utilidad como base para futuras aplicaciones Android desarrolladas por el grupo de investigación.
VII. CONCLUSIONES
La combinación del estudio detallado de la cinemática de clasificación, posición, velocidad y aceleración del mecanismo plano de cuatro barras, con la funcionalidad requerida de una aplicación diseñada específicamente para dispositivos táctiles con sistema operativo Android, permitió diseñar la secuencia de cálculos e instrucciones que facilitaron la programación de una aplicación para el análisis de mecanismos de cuatro barras.
La aplicación desarrollada es capaz de recibir datos de entrada, bien sea en cuadros de texto o mediante manipulación de la pantalla a través de la capacidad táctil de los dispositivos Android. La entrada de datos es validada contra caracteres especiales mediante la inhabilitación de tales caracteres en el teclado. La capacidad de entrada de datos mediante la función touchscreen se constituye en una característica útil en la manipulación de parámetros del mecanismo. La aplicación genera la gráfica de un mecanismo de cuatro barras predeterminado, según el tamaño de pantalla de Smartphone o Tablet en el cual esté instalada. En la gráfica se pueden editar las longitudes y orientaciones de los eslabones tocando las juntas de revoluta con los dedos y deslizándolos, mostrando la clasificación del mecanismo dibujado en tiempo real y arrojando el valor de los eslabones y ángulos.
La herramienta desarrollada fue evaluada por estudiantes del Programa de Ingeniería Mecánica de la Universidad del Atlántico que ya hubiesen cursado la asignatura Teoría de Mecanismos y Máquinas, lo que proporcionó retroalimentación para mejorar la aplicación. El aspecto de manipulación de la aplicación recibió la mejor calificación.
Actualmente la aplicación se encuentra disponible en PlayStore de Google bajo el nombre "Mecanismo4b" y puede ser instalada gratuitamente en cualquier dispositivo Android con sistema operativo 4.1 Jelly Bean o mayor. La aplicación fue registrada ante el Ministerio del Interior-Dirección Nacional de Derecho de Autor con el certificado número 13-51-86.
Mediante la creación de esta aplicación se diversifican las herramientas de enseñanza a disposición de los estudiantes de Ingeniería Mecánica, al tiempo que se contribuye a uno de los objetivos del Programa de Ingeniería Mecánica de la Universidad del Atlántico, el cual consiste en mejorar las capacidades comunicativas básicas de los estudiantes en el idioma inglés. Esto conlleva a la potencial masificación del uso de la aplicación en todo el mundo dada la gran incidencia de este idioma en la academia y la técnica.
AGRADECIMIENTOS
Los autores agradecen el apoyo de la Vicerrectoría de Investigaciones, Extensión y Proyección Social de la Universidad del Atlántico para la realización de este proyecto.
REFERENCIAS
[1] J. Shigley y J. Uiker, Teoría de Máquinas y Mecanismos, 1ra ed., México D.F.: McGraw-Hill, 2001. [ Links ]
[2] B. Baykus, E. Anli, and I. Ozkol, "Design and kinematics analysis of a parallel mechanism to be utilized as a luggage door by an analogy to a fourbar mechanism," Engineering, vol. 3, no. 4, pp. 411-421, Apr. 2011. [ Links ]
[3] N. Farhat, V. Mata, D. Rosa, and J. Fayos, "Aprocedure for estimating the relevant forces in the human knee using a four-bar mechanism," Comput. Methods Biomech. and Biomed. Engin., vol. 13, no. 5, pp. 577-587, Mar. 2010. [ Links ]
[4] H. Pinto, "Diseño óptimo de mecanismos de cuatro barras para generación de movimiento con restricciones de montaje y ángulo de transmisión", Tesis de Maestría, Universidad Nacional de Colombia, Manizales, Colombia, 2007. [ Links ]
[5] C. Galeano, C. Duque, y D. Garzón, "Aplicación de diseño óptimo dimensional a la síntesis de posición y velocidad en mecanismos de cuatro barras," Revista Facultad de Ingeniería Universidad de Antioquia, no. 47, pp. 129-144, Mar. 2009. [ Links ]
[6] R. Vásquez, J. Ramirez y G. Hernandez, "Software de simulación para mecanismos planos de cuatro barras," en XV Muestra de Trabajos de Ingeniería-Ingeniar Internacional, Editorial Universidad Pontificia Bolivariana, vol. 6, pp. 25-36, 4-6 may. 2005. [ Links ]
[7] R. Norton, "Software FOURBAR Student Edition v. 8.2," en Diseño de Maquinaria: Síntesis y Análisis de Máquinas y Mecanismos, 4ta ed. México: McGraw-Hill, 2009. [ Links ]
[8] M. Pucheta, y A. Cardona, "Software para síntesis de mecanismo planos," Mecánica Computacional, vol. 23, pp. 3369-3389, Nov. 2004. [ Links ]
[9] V. Ruiz, y N. Valencia, "Razonamiento cinemático en mecanismos eslabonados a través de ambientes computacionales," Tecné, Episteme y Didaxis, no. 23, pp. 16-30, Abr. 2008. [ Links ]
[10] D. Machado, G. Herrera, J. Roldán, y J. Díaz, "Una herramienta computacional didáctica para el análisis cinemático de mecanismos planos de cuatro barras," Revista UIS Ingenierías, vol. 14, no. 1, pp. 59-69, Ene./Jun. 2015. [ Links ]
[11] Boring Drafters, "Android Application Four Bar Link Mechanism," Agosto 2014. [En linea]. Disponible en: https://play.google.com/store/apps/details?id=rayud.fir.fourbarlinkmechanism_. ZeroBeat, "Android Application 4 Bar Linkage Formula," Septiembre 2012. [En linea]. Disponible en: https://play.google.com/store/apps/details?id=appinventor.ai_ZeroBeatPro.CRDCDR. [ Links ]
[12] N. Gómez, El Gran Libro de Android. Axel Springer, 2012. [ Links ]
[13] S. Pérochon, Android Guía de desarrollo de aplicaciones para Smartphones y Tabletas. Barcelona: ENI, 2012. [ Links ]
[14] Z. Mednieks, L. Dornin, G. Blake and M. Nakamura, Programming Android, 2nd ed. O'Reilly Media, Inc., 2012. [ Links ]
[15] J. Gironés, El Gran Libro de Android, 3ra ed. Barcelona: Marcombo, 2013. M. Báez et al., Introducción a Android. E. M. E. Editorial: Madrid, 2013. Agosto 2014. [En línea]. Disponible en: http://pendientedemigracion.ucm.es/info/tecnomovil/documentos/android.pdf. [ Links ]
[16] R. Norton, Diseño de Maquinaria: Síntesis y Análisis de Máquinas y Mecanismos, 4ta ed. México: McGraw-Hill, 2009. [ Links ]
[17] C. Barker, "A complete classification of planar fourbar linkage," Mechanism and Machine Theory, vol. 20, no. 6, pp. 535-554, 1985. "Encuesta sobre la Aplicación Mecanismo4B," [En línea]. Disponible en: http://www.e-encuesta.com/answer?testId=mMr+45xgDpo=. [ Links ]
[18] D. Myszka, Máquinas y Mecanismos, 4ta ed, México: Pearson, 2012. [ Links ]
Dairo González Miranda nació en Barranquilla, Atlántico, Colombia. Es Ingeniero Mecánico egresado de la Universidad del Atlántico. Sus intereses investigativos se orientan al uso de tecnologías que faciliten la toma de decisiones del Ingeniero Mecánico.
Eduardo Estrada Gutiérrez nació en Barranquilla, Atlántico, Colombia. Es Ingeniero Mecánico egresado de la Universidad del Atlántico. Su área de interés está orientada hacia el Diseño de Maquinaria.
Javier Roldán Mckinley nació en Barranquilla, Atlántico, Colombia. Es Ingeniero Mecánico de la Universidad del Atlántico. Obtuvo su título de MSc de la Ingeniería Mecánica con énfasis en Diseño de Maquinaria en la Universidad de Puerto Rico-Mayagüez. Obtuvo su PhD en Ingeniería Mecánica en la Universidad de la Florida (Gainesville, FL, USA) con énfasis en Dinámica, Sistemas y Control. Fue profesor de The City University of New York CUNY-LaGuardia Campus, y actualmente se desempeña como profesor de planta del Programa de Ingeniería Mecánica de la Universidad del Atlántico. Pertenece al grupo DIMER y sus intereses investigativos se orientan al control de robots, instrumentación industrial, diseño de mecanismos y máquinas y educación de la ingeniería.