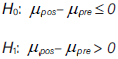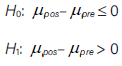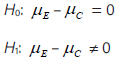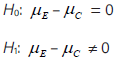INTRODUCCIÓN
El potenciar el pensamiento espacial es clave en el pregrado de diseño industrial. Varios estudios han reportado que el entrenamiento en diseño incrementa el desempeño espacial (Lin, 2016; Park et al, 2011, Onyancha et al, 2009). Usualmente las investigaciones determinan si el entrenamiento en diseño aumenta la capacidad espacial y tienden a evaluar la visualización espacial por medio de tests espaciales (Lin, 2016). En este estudio, los términos "capacidad espacial" y "pensamiento espacial" son sinónimos. Según la teoría jerárquica de la inteligencia de Philip Vernon, el pensamiento espacial es un factor grupal menor del factor grupal principal denominado "Espacial-mecánico"; a su vez, el pensamiento espacial está compuesto por factores específicos (Sattler, 2010). En consecuencia, los estudios deben decidir qué factores del pensamiento espacial incluyen en el test espacial y desde cuál autor, ya que existen varios que han expuesto los factores del pensamiento espacial, entre los cuales están:
■ Mc Gee (1979), quien afirmó que el pensamiento espacial está compuesto por dos factores, al menos: Visualización espacial y orientación espacial.
■ Lohman (1988) reconoció que el pensamiento espacial tiene al menos diez factores, pero distingue tres principales: Visualización, orientación espacial y relaciones espaciales. A este último le cambió el nombre por "velocidad de rotación".
■ Carroll (1993) indicó que el pensamiento espacial tiene cinco factores: Relaciones espaciales, velocidad de cierre, flexibilidad de cierre, velocidad perceptual y visualización.
A pesar que algunos factores sean comunes a dos autores, pueden tener distinto significado. Este estudio se basa en el pensamiento espacial de Lohman (1988), el factor denominado visualización y el test de rotación mental en 3D. Este último es la variable dependiente.
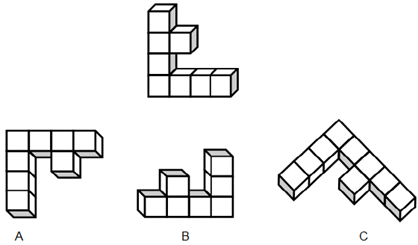
El pensamiento espacial puede definirse como la capacidad de generar, retener, recuperar y transformar imágenes visuales bien estructuradas (Lohman, 1988). Según el modelo de pensamiento espacial de Lohman, hay tres factores principales: Visualización (Vz), Orientación Espacial (SO) y Velocidad de Rotación (SR). La visualización es el más importante por la complejidad. "Los tests que pesan sobre este factor son muy diversas en otros aspectos. Algunos requieren la rotación, reflexión o plegado de figuras complejas, otros requieren que las figuras se combinen, algunos requieren múltiples transformaciones, otros no requieren transformaciones" (Lohman, 1988, p.185). Uno de los test que mide la visualización es la rotación mental en 3D, que consiste en girar mentalmente varios sólidos para identificar cuál de ellos es idéntico a uno dado (Demetriou et al., 2002). Un tipo de este test es como lo muestra la figura 1, en la cual la tarea es identificar cuál de los tres sólidos (A, B y C) es idéntico al sólido dado. Todas las figuras del test se dan impresas.
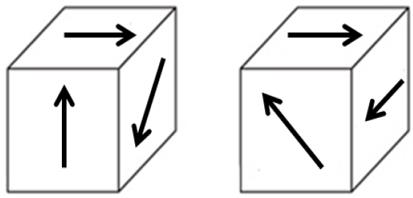
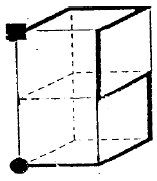
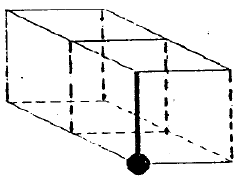
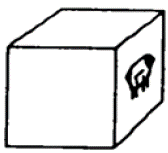
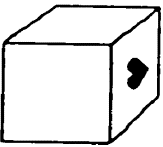
Otro test de rotación mental en 3D es la comparación de cubos (Ekstrom et al., 1976, Escrivá et al., 2018), que consiste en la presentación del dibujo de dos cubos que tienen letras, números, símbolos o figuras en tres de sus caras visibles. La tarea es indicar si uno de los cubos se obtuvo a partir de la rotación del otro, en, cuyo caso es el mismo cubo, o si, por el contrario, son cubos distintos. Por ejemplo, en la figura 2, los cubos son iguales porque uno se obtiene a partir de la rotación del otro. Un cubo con dibujos en sus caras, como el de la figura 2, también se le conoce como cubo figurativo (Gutiérrez, 1996).
Lohman (1988) resalta que las cuatro pruebas con las mayores cargas sobre el factor espacial de El Koussy, quien fue uno de los primeros en estudiar las habilidades del pensamiento espacial en el primer tercio del siglo XX, requerían que el sujeto dibujara o construyera una respuesta, y no simplemente la seleccionara de un conjunto de alternativas. Este aspecto será tenido en cuenta para el diseño de la preprueba y la posprueba en este estudio.
La variable independiente en este estudio es la construcción de sólidos en cartulina. La tarea consiste en construir el desarrollo plano de un sólido geométrico a partir de su capacidad de agua y luego armarlo. Para ello, los estudiantes deben aplicar la fórmula de volumen del respectivo sólido, hacer cálculos algebraicos, dibujar el desarrollo plano del sólido con regla, transportador (compás si es necesario), recortarlo y finalmente, armarlo. Respecto a las definiciones, los sólidos geométricos se clasifican en poliedros y cuerpos redondos.
Un poliedro es un sólido formado por un número finito de regiones poligonales denominadas caras. Los lados y los vértices de las caras se denominan, respectivamente, aristas y vértices. Cada arista de una cara es la arista de exactamente otra cara. Si dos caras se intersecan, lo hacen en una arista o un vértice. (Rojas, 2020, p. 52)
Los poliedros que se tuvieron en cuenta fueron los prismas y las pirámides. "Un cuerpo redondo es un sólido en el que por lo menos una de sus caras es una superficie curva" (Rojas, 2020, p.67). Solo se tuvo en cuenta el cono. Dado que los sólidos se construyen con cartulina, pueden contener una sustancia. Y una manera de medir la cantidad de una sustancia que puede contener es la capacidad, que "es el modo de medir la cantidad de sustancia que un recipiente puede contener" (Rojas, 2016, p.113). En este estudio, la capacidad dada corresponde a la cantidad de agua. En el proceso de construcción del sólido geométrico, el sujeto utilizará cartulina, tijeras, pegante, regla, calculadora y libros para consulta. Esto implica la manipulación sobre lo concreto y para ello se aplica la representación enactiva de Bruner. "La representación, o un sistema de representación, es un conjunto de reglas mediante las cuales se puede conservar aquello experimentado en diferentes acontecimientos" (Bruner, 2002, p.122), y ese conjunto de reglas varía de acuerdo con el tipo de representación. Las representaciones, según Bruner, son tres: enactiva, icónica y simbólica. La representación enactiva consiste en conocer algo por medio de la acción. "El enactivo es crucial para guiar la actividad y en particular lo que llamamos la actividad hábil" (Bruner, 1997, p.173) porque involucra una actividad motora sobre un instrumento con el objetivo de aprender algo, siempre que sea posible. Por ejemplo, aprender a manejar bicicleta o aprender a patinar son actividades que se aprenden manejando bicicleta y montándose sobre los patines y no viendo videos o imágenes. Es decir, se aprenden a través de la acción sobre el objeto. De manera análoga, no es lo mismo aplicar fórmulas de área total y de volumen de sólidos geométricos de manera mecánica, utilizando solo representaciones simbólicas (y si acaso, icónicas), que involucrar además la representación enactiva, porque el aprendizaje de un concepto consiste en la traducción de diversos sistemas de representación de dicho concepto, siempre que esta traducción sea posible. Y en los problemas de área y volumen de sólidos sí es posible.
El objetivo de esta investigación es determinar el efecto de la construcción de sólidos sobre la rotación 3D en un grupo de alumnos, y su correspondiente pregunta de investigación: ¿Cuál es el efecto del uso de la construcción de sólidos sobre la rotación 3D en un grupo de alumnos?
METODOLOGÍA
TIPO Y DISEÑO DE INVESTIGACIÓN
El tipo de investigación seleccionado para este estudio fue el explicativo, con diseño cuasi-experimental, con grupo control.
La tabla 1 muestra el esquema del diseño utilizado:
Tabla 1 Diseño cuasi-experimental
| Grupo | Asignación | Observaciones antes | Tratamiento | Observaciones después |
| E | No azar | O, | X, | O2 |
| C | No azar | Оз | Xo | O4 |
E: Experimental C: Control X1: Variable independiente X0: No hay tratamiento
En el diseño cuasi-experimental el grupo control y experimental no se asignan al azar; se trabajan con grupos formados previamente y su validez interna se alcanza si hay, entre otros, equivalencia, al inicio en las "observaciones antes" (O1 y О3) (Hernández et al, 2014). Posteriormente se aplica la estrategia didáctica o tratamiento al grupo experimental, mientras que al grupo control no se le aplica el tratamiento. Al final, se obtienen las "observaciones después" (O2 y O4). Las observaciones se obtienen a través de dos versiones equivalentes de una prueba para no repetir la misma prueba (Hernández et al, 2014).
POBLACIÓN
La población fueron 70 estudiantes de Diseño, distribuidos en dos grupos. Uno de 40 estudiantes de primer semestre de Diseño Gráfico, que hizo de grupo control, y el otro de 30 estudiantes de primer semestre de Diseño Industrial, que fue el grupo experimental. La muestra, en ambos grupos, fue seleccionada intencionalmente, con los siguientes criterios establecidos antes de la investigación: que los sujetos presentaran la pre prueba y la post prueba, que fueran de primer ingreso y que asistieran regularmente a las clases (Bonilla y Rodríguez, 2005). La muestra del grupo control la conformaron 36 alumnos de Diseño gráfico, de ambos géneros, con edades entre 16 y 19 años. La muestra del grupo experimental la conformaron 20 alumnos de Diseño Industrial, de ambos géneros, con edades entre 16 y 19 años.
INSTRUMENTOS
Para realizar el estudio, se aplicó un cuestionario escrito en la pre prueba y otro equivalente en la post prueba, cada uno con cinco ítems.
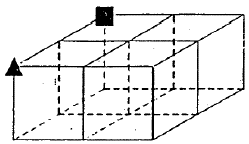
En el ítem 1 hay una red de cubos que tiene marcado un vértice con un cuadrado y otro vértice con un círculo. Hay un camino, recorriendo ocho aristas, que va del círculo al cuadrado. Hay una segunda red de cubos rotada, con respecto a la primera, que tiene marcado un vértice con un círculo y el recorrido con una arista. La tarea consiste en continuar el recorrido por las siete aristas restantes que conducen al vértice del cuadrado, que el alumno debe encontrar (Godino, 2004) (ver anexo 1).
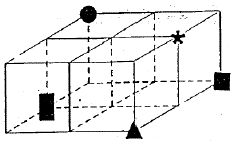
En el ítem 2 se presenta una red compuesta de cuatro cubos. Cinco de sus vértices están marcados por un cuadrado, un triángulo, una estrella, un círculo y un rectángulo. A continuación, aparece la misma red, rotada con respecto a la anterior, con solo los dos vértices marcados por el cuadrado y el triángulo. La tarea consiste en situar el vértice del círculo, de la estrella y del rectángulo (Godino, 2004) (ver anexo 1).
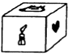
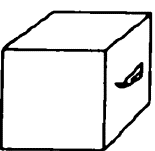
En el ítem 3 se presenta un cubo figurativo que tiene en sus tres caras visibles una vela, un corazón y una oveja. Luego se presenta el cubo rotado con solo la vela dibujada en una de sus caras, otra rotación del cubo con solo la oveja en una sus caras y otra rotación del cubo con solo el corazón dibujado en una de sus caras. La tarea en el ítem 3 es dibujar la figura en las caras en blanco, si es posible (Gutiérrez, 1992) (ver anexo 1).
La evaluación de la pre prueba y de la post prueba se hizo con el siguiente criterio de la tabla 2:
Tabla 2 Sistema de puntuación de la preprueba y posprueba
| Ítem N° | Objetivo | Puntuación |
|---|---|---|
| 1 | Encontrar y dibujar el camino que va del vértice marcado con el círculo al del cuadrado. | 0 si el dibujo es incorrecto o si no responde. 1 si el dibujo es correcto. |
| 2 | Encontrar los tres vértices sin marcar y dibujarles el círculo, la estrella y el rectángulo, respectivamente. | 0 si uno o dos o los tres vértices están marcados con los dibujos de manera incorrecta o si no responde. 1 si los tres vértices están marcados correctamente con los dibujos correspondientes. |
| 3 | Dibujar la oveja y el corazón en las caras en blanco del cubo. | 0 si un dibujo o los dos son incorrectos o si no responde. 1 si los dibujos son correctos. |
| 4 | Dibujar la vela y el corazón en las caras en blanco del cubo. | 0 si un dibujo o los dos son incorrectos o si no responde. 1 si los dibujos son correctos. |
| 5 | Dibujar la oveja en una cara en blanco, en la otra cara no es posible dibujar la vela. | 0 si el dibujo de la oveja es incorrecto o si dibuja la vela o si no responde. 1 si el dibujo es correcto. |
La tabla 3 muestra los máximos puntajes para cada ítem:
Por lo tanto, el rango del puntaje de la pre prueba y de la post prueba es de cero a cinco.
Los contenidos de las tres primeras unidades se guardaron en un archivo en formato Word en el catálogo web de la asignatura. Las unidades de geometría elemental para el grupo experimental fueron:
Unidad 1: Conceptos básicos: Puntos, rectas y planos. Ángulos planos y dirección. Puntos y rectas notables de un triángulo. Ángulos y segmentos en polígonos regulares y poliedros.
Unidad 2: Semejanza: Proporción. La razón áurea. Polígonos semejantes.
Unidad 3: Perímetro y área: Perímetro y área de polígonos inscritos en una circunferencia, de un pétalo, de una roseta de cuatro pétalos y de lúnulas.
Unidad 4: Área y volumen: Área y volumen de prismas, conos y pirámides.
En el grupo control, las cuatro unidades se guardaron en un archivo en formato Word en el catálogo web de la asignatura. Las unidades de geometría elemental para este grupo fueron:
Unidad 1: Segmentos y ángulos: puntos, rectas y planos. Segmentos. Rayos. Ángulos, el rumbo o el azimut y a ambos, la dirección opuesta.
Unidad 2: Polígonos y circunferencia. Polígonos regulares. Polígonos inscritos y circunscritos en una circunferencia.
Unidad 3: Proporción: Proporción y razón. Polígonos semejantes. Unidad 4: Área y perímetro. Perímetro y área de figuras en cuadrículas.
En consecuencia, la diferencia entre el curso del grupo experimental y el curso del grupo control estuvo en la unidad 4, en la cual los estudiantes del grupo experimental construyeron los sólidos geométricos, como se reseña a continuación, mientras que el curso del grupo control estudió el área de algunas figuras planas.
PROCESO METODOLÓGICO
Segunda etapa
El grupo experimental tuvo el curso de 16 semanas con una intensidad de 4 horas semanales y cada unidad tuvo una duración de 4 semanas. El grupo control tuvo el curso en 16 semanas con una intensidad de 3 horas semanales y cada unidad tuvo una intensidad de 4 semanas. La diferencia fue que el grupo experimental estudió la unidad de área y volumen, además de que en la primera unidad hubo problemas que involucraban el cálculo de segmentos de pirámides (apotema o altura inclinada, arista lateral y altura); mientras que el grupo control no. La metodología de la unidad de área y volumen consistió en que los alumnos buscaron las fórmulas de área y volumen de prismas, pirámides y conos. Se distribuyeron en grupos de dos. En una sesión de dos horas se le repartió a cada grupo un problema distinto que consiste en construir en cartulina un sólido geométrico con una capacidad determinada. Todos los grupos tienen acceso a las fórmulas con libro abierto o internet. Al final de esta sesión de dos horas, cada grupo debía entregar el sólido hecho en cartulina y un informe escrito de los cálculos que hicieron para elaborarlo. En las clases siguientes, cada grupo debía exponer ante sus compañeros el procedimiento y los cálculos que hicieron para construir el sólido respectivo. En caso de que un grupo no haya resuelto el problema correctamente, lo debía volver a resolver (pero no en horas de clase) y volverlo a exponer.
ANÁLISIS DE RESULTADOS
Los puntajes de la preprueba y posprueba del grupo control están en la tabla 4:
Tabla 4 Puntajes de la preprueba y posprueba del grupo control
| N° | Preprueba | Posprueba |
|---|---|---|
| 1 | 5 | 3 |
| 2 | 5 | 5 |
| 3 | 4 | 3 |
| 4 | 1 | 3 |
| 5 | 0 | 1 |
| 6 | 5 | 3 |
| 7 | 2 | 3 |
| 8 | 4 | 4 |
| 9 | 1 | 1 |
| 10 | 2 | 3 |
| 11 | 4 | 5 |
| 12 | 3 | 1 |
| 13 | 4 | 4 |
| 14 | 4 | 3 |
| 15 | 4 | 4 |
| 16 | 5 | 5 |
| 17 | 5 | 5 |
| 18 | 5 | 4 |
| 19 | 2 | 5 |
| 20 | 3 | 3 |
| 21 | 5 | 4 |
| 22 | 3 | 4 |
| 23 | 5 | 5 |
| 24 | 4 | 4 |
| 25 | 2 | 2 |
| 26 | 4 | 4 |
| 27 | 3 | 5 |
| 28 | 2 | 4 |
| 29 | 2 | 1 |
| 30 | 4 | 4 |
| 31 | 5 | 4 |
| 32 | 4 | 3 |
| 33 | 4 | 4 |
| 34 | 4 | 5 |
| 35 | 1 | 2 |
| 36 | 1 | 2 |
| x̅ | 3,36 | 3,47 |
Dado que los puntajes de la preprueba y de la posprueba tienen una distribución común y la diferencia entre ellos no se aproximan a una distribución normal, se aplicó la prueba de los rangos con signo (o prueba de los rangos con signo de Wilcoxon). Si µ pos representa la media de los puntajes del post test de la población del grupo control y µ pre la media de los puntajes de la población del mismo grupo, entonces las hipótesis son:
El valor p obtenido por la prueba es 0,06238. Debido a que el valor-p es mayor que 0,05, no se rechaza la hipótesis nula, H0, por lo que no hay diferencia estadísticamente significativa entre las medias con un 95,0% de confianza. Esto quiere decir que el estudio de la geometría sin construcción de sólidos no mejoró significativamente el nivel de rotación 3D en el grupo control.
Los puntajes del grupo experimental de alumnos se presentan en la tabla 5:
Tabla 5 Puntajes de la preprueba y : : posprueba del grupo experimental
| N° | Preprueba | Posprueba | Pos - pre |
|---|---|---|---|
| 1 | 5 | 5 | 0 |
| 2 | 4 | 4 | 0 |
| 3 | 5 | 5 | 0 |
| 4 | 4 | 4 | 0 |
| 5 | 3 | 5 | 2 |
| 6 | 2 | 3 | 1 |
| 7 | 3 | 4 | 1 |
| 8 | 3 | 4 | 1 |
| 9 | 3 | 5 | 2 |
| 10 | 3 | 5 | 2 |
| 11 | 4 | 4 | 0 |
| 12 | 3 | 5 | 2 |
| 13 | 2 | 3 | 1 |
| 14 | 4 | 3 | -1 |
| 15 | 2 | 1 | -1 |
| 16 | 5 | 5 | 0 |
| 17 | 0 | 4 | 4 |
| 18 | 5 | 5 | 0 |
| 19 | 4 | 5 | 1 |
| 20 | 3 | 4 | 1 |
| x̅ | 3,35 | 4,15 |
Dado que los puntajes de la preprueba y de la posprueba tienen una distribución común y la diferencia entre ellos no se aproximan a una distribución normal, se aplicó la prueba de los rangos con signo (o prueba de los rangos con signo de Wilcoxon). Si µ pos representa la media de los puntajes del postest del grupo experimental y µ pre pre la media de los puntajes del mismo grupo, entonces las hipótesis son:
El valor p obtenido por la prueba es 0,0047. Debido a que el valor-p es menor o igual que 0,05, se rechaza la hipótesis nula H 0 y se acepta la hipótesis alternativa H 1 , por lo que hay diferencia estadísticamente significativa entre las medias con un 95,0% de confianza. Esto quiere decir que la construcción de sólidos mejoró significativamente el nivel de rotación 3D en el grupo experimental.
ANÁLISIS ENTRE GRUPOS EN LA PREPRUEBA
Dado que los puntajes de la pre prueba de ambos grupos no proceden de una distribución normal, pero tienen la misma forma y dispersión, aplicamos la prueba de Wilcoxon-Mann-Whitney (o prueba de Wilcoxon de la suma de los rangos).
Si µ E representa la media de la población del grupo experimental y µ c la media de la población del grupo control, entonces las hipótesis son:
El valor p obtenido por la prueba es 0,818. Debido a que el valor-p es mayor que 0,05, no se rechaza la hipótesis nula, H0, por lo que no hay diferencia estadísticamente significativa entre las medias con un 95,0% de confianza. Esto quiere decir que los dos grupos son parejos en el nivel de rotación 3D al inicio del estudio.
ANÁLISIS ENTRE GRUPOS EN LA POSPRUEBA
dado que los puntajes de la preprueba de ambos grupos no proceden de una distribución normal, pero tienen la misma forma y dispersión, aplicamos la prueba de Wilcoxon-Mann-Whitney (o prueba de Wilcoxon de la suma de los rangos).
Si µ E representa la media de la población del grupo experimental y µ C la media de la población del grupo control, entonces las hipótesis son:
El valor p obtenido por la prueba es 0,00179. Debido a que el valor-p es menor o igual que 0,05, se rechaza la hipótesis nula, H 0 , y se acepta la hipótesis alternativa, por lo que hay diferencia estadísticamente significativa entre las medias con un 95,0% de confianza. Esto quiere decir que el nivel de rotación 3D en el grupo experimental es significativamente mayor al nivel de rotación 3D del grupo control. Esta es la evidencia causal entre la variable independiente y la variable dependiente en el grupo experimental.
Para este análisis estadístico se consultaron las pruebas no paramétricas en Siegel y Castellan (2005).
CONCLUSIONES
En este estudio se propuso como objetivo determinar el efecto de la construcción de sólidos sobre la rotación 3D en un grupo de alumnos y el análisis estadístico arrojó que hay diferencia significativa en el nivel de rotación 3D en la posprueba entre el grupo experimental y el grupo control, estableciendo una relación causal entre la variable independiente (construcción de sólidos) y la variable dependiente (rotación 3D) en el grupo de estudiantes. Este resultado sugiere que el estudio del volumen y el área en 3D, usando diversos sistemas de representación (enactivo, icónico y simbólico), aumenta significativamente un factor del pensamiento espacial en los estudiantes, en este caso, la rotación en 3D. Este resultado corrobora lo establecido por Bruner (2002): "Tener la imagen del nudo en la mente, o dibujada en un papel, no es lo mismo que hacer el nudo, aunque la imagen pueda proporcionar un esquema para organizar secuencialmente las acciones" (p.122). Similarmente, que el estudiante tenga en la mente la imagen de un poliedro o la tenga dibujada al resolver solo de manera algebraica un problema de volumen, no es lo mismo que el estudiante tenga que dibujar con instrumentos el desarrollo plano de dicho poliedro para luego armarlo, ya que esta última exige un dominio progresivo de tres sistemas de representación y su traducción Bruner (2002).
Entre las limitaciones de este estudio está lo reducido del tamaño de la muestra y el estudio de un solo factor (rotación en 3D) del pensamiento espacial.