Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
DYNA
Print version ISSN 0012-7353On-line version ISSN 2346-2183
Dyna rev.fac.nac.minas vol.72 no.146 Medellín May/Aug. 2005
ESTUDIO DEL MODELO DE DESGASTE PROPUESTO POR ARCHARD
STUDY OF THE MODEL OF WEARING PROPOSED BY ARCHARD
FABIO ALEXANDER SUÁREZ BUSTAMANTE
Ingeniero Mecánico - Grupo de Tribología y Superficies Universidad Nacional de Colombia Medellín
JUAN MANUEL VÉLEZ RESTREPO
Profesor Asociado, Grupo de Tribología y Superficies Universidad Nacional de Colombia Medellín. jmvelez@unalmed.edu.co
Recibido para revisar 7 de Junio de 2004, aceptado 2 de Agosto de 2004, versión final 4 de Febrero de 2005
RESUMEN: El comportamiento de componentes de máquinas y de materiales necesita ser optimizado para reducir los costos de operación en las plantas industriales. Este hecho ha impulsado la Tribología, un área relacionada con el estudio de la fricción, la lubricación y el desgaste. Uno de los principales objetivos de esta área del conocimiento es elaborar modelos matemáticos para expresar la variación del desgaste durante el contacto de superficies en movimiento, con el fin de predecir la vida útil de los elementos de máquinas. El modelo de Archard para desgaste por deslizamiento en seco, formulado en 1953, es un modelo clásico que plantea una variación del desgaste inversamente proporcional a la dureza del material y directamente proporcional a la carga aplicada. En el presente trabajo, se ha utilizado el método de modelamiento de problemas físicos, propuesto por Asbhy, para analizar los modelos propuestos por Archard (Modelo de contactos múltiples en superficies rugosas y modelo de desgaste mecánico). Con base en él se ha podido realizar un análisis profundo a dichos modelos, mostrando un panorama más amplio del modelo de Archard; se discuten aspectos no mostrados en los textos y artículos de tribología, donde el tratamiento dado a este modelo resulta ser superficial, desconociendo las limitaciones y la perspectiva que tuvo Archard sobre los aspectos que deberían considerarse en un modelo de desgaste.
PALABRAS CLAVES: Tribología, Desgaste, modelos, Archard, Método de Ashby.
ABSTRACT: The performance of machine parts and materials, needs to be optimized to reduce operation costs in the industrial plants. This fact has driven the Tribology, a knowledge area related to friction, lubrication and weariness.(sug: look up a better word for desgaste!) One of the main goals of Tribology is to search for mathematic models to express the wear factor rate during the contact of surfaces in movement in order to predict the useful life of the machine parts. The Archard model for dry sliding weariness, presented in 1963, establishes a directly proportional relation between the applied load and wear factor rate, and an inversely proportional relation between hardness and wear factor rate. In this work the method for modelling material problems proposed by Ashby has been applied to analyze Archards models (Multiple contacts model in rough surfaces and mechanical weariness). With this approach, it has been possible to implement a profound analysis of such models; it was possible to show a wide picture about the classic weariness model proposed by Archard. Aspects not shown in tribology books and papers are discussed here, where the model is shown in a superficial way, overlooking the limitations and future perspectives that in the moment Archard had about aspects that should had been considered in the weariness model.
KEY WORDS: Tribology, weariness, models.
1. INTRODUCCIÓN
Desde la década del 50 se ha trabajado fuertemente en la formulación de modelos que permitan expresar matemáticamente la variación del desgaste durante el contacto de superficies en movimiento, sin lograrse un avance significativo. Las principales dificultades se originan en la presencia de factores microscópicos, entre los cuales puede mencionarse la calidad superficial, las heterogeneidades del material y la temperatura localmente desarrollada, elementos normalmente dejados de lado por la mecánica clásica. La mayoría de los modelos reportados en la literatura han sido desarrollados para sistemas tribológicos específicos - un par de materiales en particular, una geometría de contacto determinada y un ambiente y lubricante definidos – sometidos a condiciones de operación también definidas.
Las primeras investigaciones sobre desgaste obtuvieron ecuaciones empíricas, de la forma 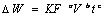 , (donde ΔW= pérdida de masa, F=Fuerza, V=velocidad y T=tiempo; a,b,c son constantes) desarrolladas para obtener datos específicos útiles en la construcción de motores y componentes de maquinaria. El desarrollo de nuevas tecnologías, aeroespacial e industrial, en las décadas del 50 y 60 impulsó los estudios de adhesión y desgaste apoyado en ecuaciones basadas en la mecánica del contacto que utilizan propiedades del material, tales como su módulo de elasticidad E y dureza H. En esa época se produjeron grandes avances en la identificación y el entendimiento de los mecanismos asociados a los diferentes procesos de desgaste: deslizamiento, abrasión, erosión y fretting. Conceptos como área real de contacto, adhesión, transferencia de material entre superficies en contacto, ángulos críticos para abrasión y erosión y la mecánica del contacto de superficies rugosas fueron bien desarrollados[1].
, (donde ΔW= pérdida de masa, F=Fuerza, V=velocidad y T=tiempo; a,b,c son constantes) desarrolladas para obtener datos específicos útiles en la construcción de motores y componentes de maquinaria. El desarrollo de nuevas tecnologías, aeroespacial e industrial, en las décadas del 50 y 60 impulsó los estudios de adhesión y desgaste apoyado en ecuaciones basadas en la mecánica del contacto que utilizan propiedades del material, tales como su módulo de elasticidad E y dureza H. En esa época se produjeron grandes avances en la identificación y el entendimiento de los mecanismos asociados a los diferentes procesos de desgaste: deslizamiento, abrasión, erosión y fretting. Conceptos como área real de contacto, adhesión, transferencia de material entre superficies en contacto, ángulos críticos para abrasión y erosión y la mecánica del contacto de superficies rugosas fueron bien desarrollados[1].
En las décadas posteriores -1970-1980- el desarrollo de la instrumentación avanzada (microscopio electrónico de barrido, instrumentos para el análisis de la superficie, etc.) facilitó la investigación sobre el estado de las superficies permitiendo la identificación de los mecanismos presentes durante el desgaste, tanto a nivel de laboratorio como en la industria. Las técnicas computacionales, por otro lado, permitieron el análisis de los esfuerzos de contacto y de la temperatura en la superficie impulsando el modelado numérico de problemas relacionados con la interacción de superficies.
Holm y Archard[2] desarrollaron un modelo en el cual la rapidez de desgaste ( ) es proporcional a la carga normal aplicada (P) e inversamente proporcional a la dureza del material (H) relacionados a través de una constante k. Estos autores obtuvieron una ecuación de forma simple, conocida como ecuación de Archard:
) es proporcional a la carga normal aplicada (P) e inversamente proporcional a la dureza del material (H) relacionados a través de una constante k. Estos autores obtuvieron una ecuación de forma simple, conocida como ecuación de Archard:
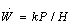
Este modelo, aparentemente muy sencillo, es empleado a menudo en aplicaciones de ingeniería y ha servido de base para el desarrollo de modelos más elaborados que intentan dar una interpretación más amplia a los fenómenos presentes en la interacción de superficies.
Ashby[3] propuso un método para desarrollar Modelos Físicos de problemas en el área de materiales; éste es descrito en la carta de flujo mostrada en la Figura 1. En ella se resumen los estados involucrados en el desarrollo de un modelo, destacándose su naturaleza iterativa. Sin embargo, no todos los modelos requieren pasar por todos estos estados y siempre se debe recordar que un modelo debe ser tan sencillo como sea posible, mas no debe ser simplista La sencillez de un modelo constituye su esencia.
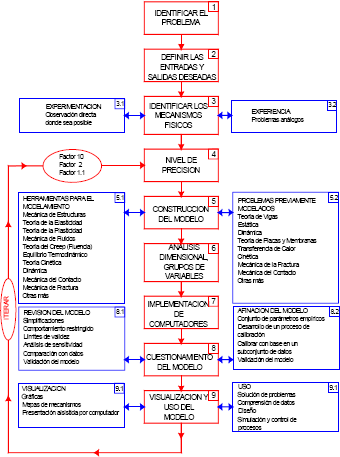
Figura 1. Carta de Ashby
Figure 1. Ashby letter
El presente trabajo tuvo como objetivo analizar el modelo de desgaste para deslizamiento en seco propuesto por Archard, a la luz del método sugerido por Ashby para modelar problemas físicos de materiales.
2. CONTACTO ENTRE SUPERFICIESEl contacto entre superficies ocurre básicamente a través de las cimas más altas de sus asperezas, y por lo tanto, el área real de contacto es mucho menor al área aparente. El área real está determinada por la deformación experimentada por los materiales en estas regiones bajo las condiciones de carga aplicada. El área de contacto real es la suma de los contactos individuales que ocurren entre asperezas y por lo tanto compromete tres elementos básicos de éstas: número, tamaño y distribución. Estos tres elementos influyen en la conductancia eléctrica, la temperatura y las deformaciones asociadas con el contacto. Además, tiene influencia en la magnitud de la transferencia de material entre superficies rozantes y en la rapidez del desgaste.
Los modelos idealizados por la mecánica asumen que el área de contacto se halla confinada en una región que depende de la geometría de los cuerpos, las propiedades de sus materiales y las condiciones de las cargas aplicadas. Es posible, entonces, plantear modelos de deformación para una aspereza cónica, esférica o piramidal. Sin embargo, existe un problema fundamental: ¿Cómo aplicar los resultados obtenidos con estos modelos a casos más generales, donde se presentan contactos múltiples?. Es necesario, entonces, hacer algunas suposiciones sobre la forma y distribución de las áreas individuales de contacto y deducir su efecto en el comportamiento de las superficies para diversos estados de deformación, considerando la presencia o ausencia de películas de óxidos superficiales.
Alrededor de este problema gira el modelamiento planteado por Archard en su artículo Contact and Rubbing of Flat Surfaces, 1953[2], en el cual trató de determinar las relaciones entre la carga, la conductancia y el área real de contacto para contactos múltiples entre asperezas, tal como ocurre entre superficies rugosas, y que luego utilizó para la formulación de su modelo de desgaste mecánico.
A continuación se trata de manera separada los dos modelos propuestos por Archard. Para esto se ha tomado como base la visión que el mismo Archard tenía sobre este problema y finalmente se realizan algunos comentarios pertinentes sobre el modelo planteado con base en los avances que se han realizado en el tema y algunos aportes propios[4].
3. MODELO DE CONTACTOS MÚLTIPLES
El problema consiste en determinar las relaciones existentes entre la carga normal, la conductancia y el área real de contacto en condiciones en las cuales existen múltiples contactos distribuidos de cierta forma al interior del área de contacto aparente.
Las variables de entrada definidas son:
- Carga Normal: P
- Dureza o presión de flujo del material: pm
- Módulo de elasticidad: E
- Conductividad específica de los materiales:
- Resistividad por unidad de área de una película protectora:
- Las variables de salida definidas son:
- Área de contacto real: A
- Conductancia: G
3.1 IDENTIFICACIÓN DE LOS MECANISMOS
Dependiendo de la intensidad de la carga en cada uno de los contactos, de la geometría macro de las asperezas, de las propiedades elásticas y mecánicas de los materiales y de la presencia de películas de óxidos o de otro tipo en las superficies, Archard identificó los siguientes contactos individuales:
- Contacto elástico de carácter puramente metálico (ausencia de películas entre las superficies en contacto).
- Contacto elástico en presencia de una película.
- Contacto plástico puramente metálico.
- Contacto plástico en presencia de una película.
Por lo general coexisten los diversos tipos de contactos, y en especial, si se trata de materiales metálicos donde la oxidación constituye un factor importante. Sin embargo, en el modelo se analizan los mecanismos propuestos de manera independiente.
3.2 NIVEL DE PRECISIÓN DEL MODELO
Este modelo no asigna una valoración a su nivel de precisión, pese a las simplificaciones que se hicieron y que han permitido comparar el modelo con los resultados de ciertos experimentos realizados en situaciones muy especiales. Esto puede ser debido a la dificultad de determinar la influencia de cada uno de los tipos de contacto.
3.3 CONSTRUCCIÓN DEL MODELO
Con base en los desarrollos hechos por Hertz, suponiendo que las asperezas tienen forma hemisférica y que su, para un contacto es solo de naturaleza elástica, el radio de la zona de contacto está dado por la expresión
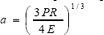
donde, R y E son el radio y el módulo reducidos del sistema respectivamente, y vienen dados por las siguientes expresiones,
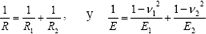
Si se considera el contacto entre una aspereza de radio R y una superficie plana (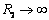 ), y además se asume que
), y además se asume que 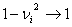 , esta expresión puede simplificarse de la siguiente manera
, esta expresión puede simplificarse de la siguiente manera
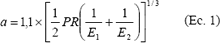
donde E1 y E2 son los módulos de elasticidad de la aspereza y de la superficie plana respectivamente.
Los trabajos de Bowden & Tabor[5] muestran que para condiciones de flujo plástico en materiales que prácticamente exhiben un comportamiento elástico - perfectamente plástico, la presión de flujo permanece constante y sólo depende de la relación entre la carga normal aplicada y el área real de contacto. Así el radio del área de contacto viene dado por la expresión

La conductancia en un contacto metálico debida a la constricción está dada por la expresión

donde 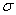 es la conductividad específica de los dos materiales.
es la conductividad específica de los dos materiales.
Para el caso de un contacto entre asperezas en presencia de una película, la conductancia estaría dada por

despreciando el efecto de la constricción sobre ésta.
Si se considera una aspereza deformable de forma hemisférica presionada contra una superficie plana, lisa y rígida (Ver Figura 2) se pueden obtener expresiones que relacionen el área de contacto A, la carga P y la conductividad G con el acercamiento x, experimentado entrer la superficie rígida y puntos muy lejanos de la zona de contacto. Estas expresiones tienen las siguientes formas:

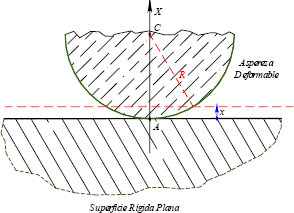
Figura 2. Contacto entre una aspereza deformable y una superficie plana y rígida.
Figure 2. Contact between a deformable harshness and a flat and rigid surface.
Y sus coeficientes pueden determinarse como se muestra a continuación.
De la geometría mostrada en la Figura 2 se deduce que 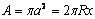 , donde
, donde 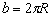 y
y 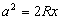 . Esta ecuación aplica para el caso de un contacto en condiciones de deformación plástica. Para el caso elástico, al evaluar el desplazamiento experimentado por el punto A y haciendo uso de las ecuaciones de Hertz, se deduce que el valor de b es la mitad del anterior,
. Esta ecuación aplica para el caso de un contacto en condiciones de deformación plástica. Para el caso elástico, al evaluar el desplazamiento experimentado por el punto A y haciendo uso de las ecuaciones de Hertz, se deduce que el valor de b es la mitad del anterior, 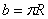 .
.
En el caso de la deformación plástica la presión de flujo está dada por la relación 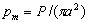 , de donde se deduce que
, de donde se deduce que 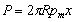 . En el caso de deformación elástica, al considerar que
. En el caso de deformación elástica, al considerar que 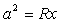 , se tiene que
, se tiene que 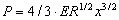 .
.
En el caso de la conductancia se tienen las siguientes posibilidades:
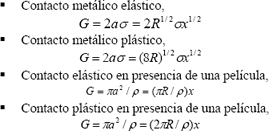
Combinando las expresiones 5 se pueden obtener las siguientes relaciones generales para el área de contacto y la conductancia en función de la carga
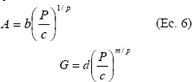
Para generar un modelo de múltiples áreas de contacto, Archard consideró una superficie plana rugosa deformable puesta en contacto contra otra superficie plana, lisa y rígida (Ver Figura 3). Se supone que la superficie deformable se halla compuesta sólo por un gran número asperezas hemisféricas de igual radio de curvatura R y cuyas alturas se hallan distribuidas de manera uniforme. Archard hizo uso de una distribución discreta para las alturas de las asperezas, lo cual se ajusta bien a la realidad; para esto, consideró que en la dirección x existe una aspereza en cada una de las siguientes coordenadas: x = 0, h, 2h,... , donde 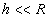 . Luego, existen M asperezas por unidad de profundidad en x,
. Luego, existen M asperezas por unidad de profundidad en x, 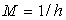 .
.
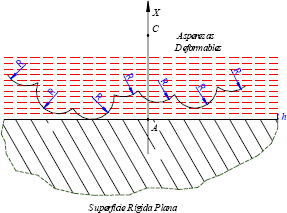
Figura 3. Situación propuesta para el modelo de múltiples contactos.
Figure 3. Propose situation for the model of multiple contacts.
Con base en estas consideraciones se puede demostrar que el área de contacto y la conductancia se relacionan con la carga normal de la siguiente manera:
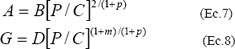
donde B, C y D son parámetros cuyos valores dependen de las constantes M, b, c d, p y m. Sus relaciones pueden consultarse en la referencia 5.
3.4 CUESTIONAMIENTO DEL MODELO
La idea de Archard fue determinar la relación existente entre el área de contacto, la conductancia y la carga aplicada, encontrando relaciones del tipo 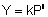 . Archard centró su análisis en los exponentes de estas relaciones, sin considerar los coeficientes de proporcionalidad que acompañan la carga normal. La Tabla 1 presenta un resumen de las relaciones para los diferentes tipos de contacto que él logró identificar.
. Archard centró su análisis en los exponentes de estas relaciones, sin considerar los coeficientes de proporcionalidad que acompañan la carga normal. La Tabla 1 presenta un resumen de las relaciones para los diferentes tipos de contacto que él logró identificar.
Tabla 1. Resumen de las relaciones teóricas entre el área real de contacto, la conductancia y la carga normal para los diferentes tipos de contactos.
Table 1. Summary of the theoretical relations between the real area of contact, the conductance and the normal charge for the different types from contacts.
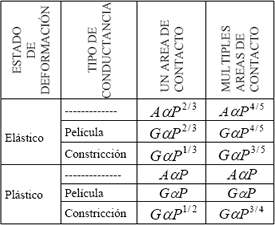
En una relación de la forma 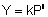 , el exponente n muestra la manera como se relacionan las dos variables P y Y; mientras que el coeficiente K simplemente amplifica o reduce los valores obtenidos para Y sin alterar la forma como están relacionas Y y P.
, el exponente n muestra la manera como se relacionan las dos variables P y Y; mientras que el coeficiente K simplemente amplifica o reduce los valores obtenidos para Y sin alterar la forma como están relacionas Y y P.
En la tabla se puede observar que al pasar de un contacto a múltiples contactos, el valor de n tiende a incrementarse, a lo sumo hasta la unidad, independiente del régimen de deformación que se considere; en el caso de n=1 el comportamiento exhibido sería lineal.
Tanto para el área como para la conductancia se nota un incremento del valor de n cuando se pasa del régimen elástico al plástico para las dos condiciones de contacto analizadas.
Para las relaciones entre la carga normal y el área de contacto se observa que solamente existen variaciones significativas de n al pasar del modelo de un contacto al de múltiples contactos; para el caso de contactos plásticos el tipo de distribución de las asperezas no altera la relación final obtenida, la cual es equivalente a la de un solo contacto.
Experimentos de contacto con geometrías que se pueden aproximar a la de un contacto simple, caso de cilindros cruzados por ejemplo, muestran que los valores de los exponentes n en las relaciones de la forma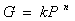 son muy similares a los predichos por el modelo de un contacto. Los valores de n varían entre los dados teóricamente para el caso de contactos simples y la unidad, es decir,
son muy similares a los predichos por el modelo de un contacto. Los valores de n varían entre los dados teóricamente para el caso de contactos simples y la unidad, es decir, 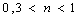 . Algunas diferencias pequeñas se explican mediante la combinación de condiciones de deformación elástica y plástica y de la naturaleza metálica del contacto. Mas, esta explicación no aplica a casos en los cuales se estudian contactos múltiples, pues la forma en que estos se distribuyen modifica sustancialmente los resultados y se convierte en un factor importante a considerar. Basta con comparar los valores de n entre las condiciones correspondientes para el caso de un contacto y el de contactos múltiples.
. Algunas diferencias pequeñas se explican mediante la combinación de condiciones de deformación elástica y plástica y de la naturaleza metálica del contacto. Mas, esta explicación no aplica a casos en los cuales se estudian contactos múltiples, pues la forma en que estos se distribuyen modifica sustancialmente los resultados y se convierte en un factor importante a considerar. Basta con comparar los valores de n entre las condiciones correspondientes para el caso de un contacto y el de contactos múltiples.
Para cualquier distribución de las alturas de las asperezas asumida para el modelo de contactos múltiples, los valores de n estarán comprendidos entre 0.3 y la unidad siempre y cuando al incrementar la carga normal se incremente el número de contactos y su tamaño. Esto sugiere que el modelo desarrollado no es muy significativo o dicho en otras palabras, sólo constituye uno de los casos particulares posibles; sin embargo, puede ser útil como un buen punto de partida. Esto muestra que para el caso de la conductancia, el modelo empleado para representar las superficies influye significativamente en los resultados obtenidos.
A partir de experimentos realizados en la época en la cual se construyó el modelo, se han determinado valores de n que se ajustan bastante bien con los predichos para las condiciones de deformación y de la naturaleza metálica del contacto. Algunos de estos trabajos pueden verse en detalle en el primer capítulo del texto de Bowden y Tabor, The friction and lubrication of solids[5]. Además en estos trabajos se confirma experimentalmente que un incremento en la carga aumenta tanto el número como el tamaño de los contactos.
Archard afirma que su modelo de múltiples contactos sólo tiene en cuenta una escala de la estructura de las imperfecciones, la de la rugosidad y que un modelo para este tipo de condiciones debe considerar como mínimo dos niveles estructurales, el de las ondulaciones (longitudes de onda de gran tamaño) y el de las rugosidades (longitudes de onda pequeñas). Ver Figura 4.
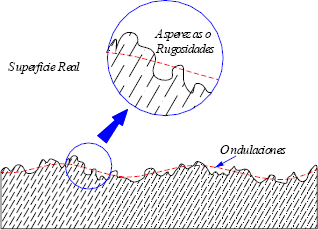
Figura 4. Niveles de la estructura de las imperfecciones de la superficie (En realidad las asperezas son suaves, poco curvas, de manera similar a las ondulaciones sólo que a una escala menor).
Figure 4. Levels of the structure of the imperfections of the surface (In fact the harshness is smooth, little curved, similar to the ondulations in smaller scale).
La macro-estructura de las imperfecciones (las ondulaciones), determina las zonas donde las superficies más probablemente entran en contacto, y en estas zonas, los contactos ocurren a nivel de las rugosidades. De aquí que, muy probablemente, la mayoría de las asperezas se hallan deformadas plásticamente, mientras que a nivel de las ondulaciones, éstas se hallan en un estado de deformación elástico. Los experimentos llevados a cabo para la determinación de la conductancia y de los tamaños promedio de los contactos en función de la carga normal aplicada, sugieren que las medidas de la resistencia de contacto dan información sobre las áreas de contacto generales o de influencia asociadas con las ondulaciones; y esto limita el uso de estos métodos para los estudios sobre la fricción, la cual tiene su origen a nivel de los contactos íntimos entre las asperezas básicamente.
3.5 VISUALIZACIÓN Y USO DEL MODELO
A pesar de su simpleza (o limitaciones) y a los comentarios antes realizados, el modelo obtenido puede plasmarse en un grupo de expresiones matemáticas tales como las ecuaciones 7 y 8, o de una manera más sencilla mediante el uso de la Tabla 1 donde se resumen los diferentes tipos de relaciones encontradas para la conductancia, el área de contacto y la carga normal, con base en los supuestos realizados.
Una aplicación dada a este modelo se muestra a continuación. Inicialmente, a partir de este modelo de múltiples contactos, Archard construyó su modelo de desgaste mecánico, del cual deriva su famosa ley de desgaste lineal en función de la carga normal.
4. MODELO DE DESGASTE MECANICO PROPUESTO POR ARCHARD
El problema consiste en deducir unas leyes simples para explicar los procesos de desgaste mecánico cuyo comportamiento es lo suficientemente regular como para permitir hacer un tratamiento teórico.
Las variables de entrada definidas son:
- Carga Normal: P
- Dureza o presión de flujo del material: pm
- Módulo de elasticidad: E
- Las variables de Salida definidas son:
- Tasa de Desgaste : W
- Factor de Probabilidad: K
4.1 IDENTIFICACIÓN DE LOS MECANISMOS FÍSICOS
A partir de los estudios y discusiones llevadas cabo sobre el fenómeno del desgaste por varios investigadores como Holm, Burwell & Strang y Rabinowicz & Tabor, Archard propone los siguientes mecanismos para la remoción de partículas de desgaste con base su forma y el tipo de deformación:
- Remoción por grumos desde zonas de contactos de naturaleza plástica.
- Remoción por grumos desde zonas de contactos de naturaleza elástica.
- Remoción por capas desde zonas de contactos de naturaleza plástica.
- Remoción por capas desde zonas de contactos de naturaleza elástica.
4.2 NIVEL DE PRECISIÓN
en principio el modelo planteado no presenta la posibilidad de evaluar (o al menos de establecer) un nivel de precisión. Para poder hacerlo, es necesario interactuar con arreglos experimentales, los cuales influyen en los valores encontrados para la constante K. Por esto se trata de un modelo de gran simplicidad que al aplicarlo a una condición particular, exige un conocimiento previo detallado de los fenómenos involucrados y de las variaciones de algunos de sus parámetros.
A diferencia de algunos modelos totalmente analíticos como los obtenidos en la teoría de la elasticidad, por ejemplo para elementos curvos sometidos a flexión en los cuales es posible hacer algunas simplificaciones con respecto a su geometría y valorar la forma en que es alterada la respuesta esperada, en el caso del modelo de desgaste es necesario recurrir a la parte práctica o experimental para poder construir el modelo.
4.3 CONSTRUCCIÓN DEL MODELO
Inicialmente cuatro premisas son hechas para la construcción del modelo, a saber,
4.3.1 El tamaño y la distribución del área total de contacto
Para esto se emplea el modelo de múltiples contactos asumiendo la misma distribución uniforme en las alturas de las asperezas y considerando que ambas superficies en contacto son rugosas.
4.3.2 La duración de los contactos
Se asume que en la medida en que un contacto va desapareciendo (se reduce el área de contacto), en otro lugar de la zona de contacto aparente, un nuevo contacto se irá formando de manera que, el área total de contacto permanece constante independiente de la geometría de las asperezas (esférica por ejemplo).
4.3.3 La forma de las partículas de desgaste
Al suponer asperezas de forma hemisféricas, se hacen dos supuestos con respecto al volumen de las partículas de desgaste 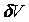 así,
así,
4.3.3.1 Remoción por capas. 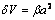 , donde
, donde 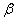 es una constante que representa el espesor de la capa removida; y por lo tanto, para este caso, el espesor de capa es independiente de la carga normal y del radio del área de contacto.
es una constante que representa el espesor de la capa removida; y por lo tanto, para este caso, el espesor de capa es independiente de la carga normal y del radio del área de contacto.
4.3.3.2 Remoción por grumos. 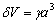 , donde
, donde 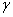 es una constante, la cual indica que la profundidad a la cual el material es desgarrado es proporcional al radio del área de contacto, es decir, estadísticamente la forma de las partículas de desgaste es independiente de su tamaño (son geométricamente semejantes).
es una constante, la cual indica que la profundidad a la cual el material es desgarrado es proporcional al radio del área de contacto, es decir, estadísticamente la forma de las partículas de desgaste es independiente de su tamaño (son geométricamente semejantes).
4.3.4 El factor de probabilidad
Independiente del tamaño de los contactos, no todos los contactos generan partículas de desgaste y por lo tanto, para cada sistema se define un factor genérico K, que da cuenta de la probabilidad de que se forme una partícula de desgaste a partir de un contacto dado. Este factor de probabilidad sólo aplica a un rango de condiciones experimentales para las cuales el proceso de desgaste posea las mismas características.
Al definir la tasa de desgaste W como el volumen desgastado por unidad de distancia recorrida, se tiene entonces que ésta está dada por la suma de las contribuciones de los contactos donde se generan partículas de desgaste durante un periodo de tiempo específico y puede expresarse de la siguiente manera con base a los supuestos b, c y d,
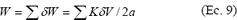
Al hacer uso del modelo de contactos múltiples se encuentran expresiones que relacionan la tasa de desgaste y la carga normal para cada tipo de mecanismo propuesto. Estas relaciones tienen la forma donde 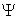 y
y 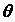 son constantes características del mecanismo considerado.
son constantes características del mecanismo considerado.
Al suponer partículas de desgaste de forma hemisférica se tiene que 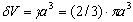 , de donde
, de donde 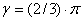 ; y por lo tanto, las dos expresiones que se deducen para la tasa de desgaste considerando el mecanismo de remoción por grumos tienen la siguiente forma para el mecanismo elástico y el plástico:
; y por lo tanto, las dos expresiones que se deducen para la tasa de desgaste considerando el mecanismo de remoción por grumos tienen la siguiente forma para el mecanismo elástico y el plástico:
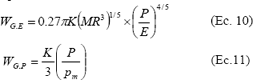
De manera similar se puede hallar que para el caso de remoción por capas y para cada tipo de deformación, las tasas de desgaste se pueden relacionar con la carga de la siguiente manera,
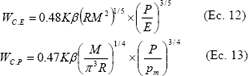
En la Tabla 2 se hace un resumen de las relaciones entre la tasa de desgaste y la carga normal para los mecanismos propuestos.
Tabla 2. Resumen de las relaciones teóricas entre la tasa de desgaste y la carga normal para los diferentes tipos de contactos.
Table 2. Summary of the theoretical relations between the rate of wearing and the normal charge for the different types from contacts.
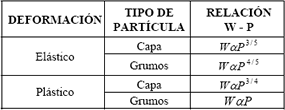
Al considerar las contribuciones de los cuatro mecanismos identificados, el modelo de desgaste mecánico propuesto por Archard se puede escribir en su forma más general de la siguiente manera,
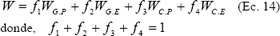
Con base en los resultados de los experimentos llevados a cabo por Bowden & Tabor, Archard supone que el mecanismo de remoción por grumos mediante deformación plástica es el de mayor probabilidad de ocurrencia, y por ende el más significativo, ya que es el que mejor coincide con la evidencia experimental. De esta manera, haciendo que 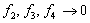 , su modelo se reduce a
, su modelo se reduce a
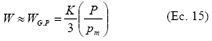
De donde se plantea que la tasa de desgaste se comporta como una función lineal de la carga aplicada y es inversamente proporcional a la presión de flujo plástico (o en su defecto a la dureza) del material más blando.
4.4 CUESTIONAMIENTO DE ARCHARD A SU MODELO
Archard hace notar que su resultado es básicamente el mismo que obtuvo Holm, sólo que en su modelo se sustituye el concepto de remoción de átomos por el de remoción de partículas, haciendo esto que el desgaste no sea visto a escala atómica sino a una escala de aglomerados de átomos que constituyen las partículas de desgaste.
Al considerar un mecanismo de remoción por grumos procedentes de una deformación plástica, resulta innecesario el empleo de un modelo de contactos múltiples en el cual se asuma una distribución determinada para las alturas de las asperezas. De esta manera, el modelo de desgaste desarrollado resulta ser independiente del modelo empleado para representar las superficies y sólo es necesario realizar las suposiciones sobre la duración de los contactos y la forma de las partículas de desgaste.
Un resultado semejante puede ser obtenido a partir de un contacto individual y considerando el mecanismo de remoción por grumos procedentes de una deformación plástica. El volumen de la partícula es proporcional al cubo del radio del contacto 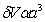 , y la distancia de deslizamiento efectiva
, y la distancia de deslizamiento efectiva 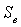 , es proporcional al radio del área del contacto
, es proporcional al radio del área del contacto 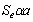 ; por lo tanto, la tasa de desgaste
; por lo tanto, la tasa de desgaste 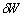 resulta ser proporcional al cuadrado del radio de área del contacto
resulta ser proporcional al cuadrado del radio de área del contacto 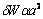 . Dado que la carga
. Dado que la carga 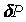 también es proporcional al cuadrado del radio de área del contacto
también es proporcional al cuadrado del radio de área del contacto 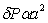 , entonces se concluye que para este contacto, la tasa de desgaste es proporcional a la carga allí aplicada
, entonces se concluye que para este contacto, la tasa de desgaste es proporcional a la carga allí aplicada 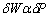 . Al extender este razonamiento a todos los contactos, se tiene que la tasa de desgaste total W es proporcional a la carga normal aplicada P,
. Al extender este razonamiento a todos los contactos, se tiene que la tasa de desgaste total W es proporcional a la carga normal aplicada P, 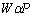 .
.
En lo referente a la forma de las partículas y a la duración de los contactos, al hacer supuestos diferentes sólo se alteraría la expresión obtenida en un factor constante.
Los resultados experimentales obtenidos por varios investigadores (Bowden & Tabor y Burwell & Strang) y por el propio Archard, le permitieron validar su modelo. Las conclusiones más importantes que este autor muestra en la discusión que presenta en su artículo son las siguientes:
- La tasa de desgaste es proporcional a la carga normal: ésto ha sido corroborado en experimentos de desgaste continuado y de transferencia efectuados con diversos tipos de materiales (metales y no metales). En algunos casos aplica también a sistemas tribológicos lubricados, en los cuales el lubricante es un elemento inerte. También puede observarse este comportamiento en intervalos limitados de condiciones impuestas a otros sistemas que exhiben comportamientos más complejos en otras condiciones. De esta manera, Archard es consciente de las limitaciones de su modelo, ya que como él mismo lo expresa, la presencia de factores mecánicos y químicos involucrados en los procesos de desgaste limita la aplicación general de su teoría.
- La tasa de desgaste es independiente del área aparente de contacto: de hecho, en el modelo propuesto puede verse que el cociente
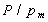 representa el área real de contacto (al menos a condiciones ambiente), y que por lo tanto, éste plantea que la tasa de desgaste es proporcional a dicha área. Experimentalmente, pruebas realizadas en tribómetros del tipo pin sobre anillo, donde el pin se ha caracterizado por poseer inicialmente su cara de contacto plana, han permitido corroborar esta afirmación. Ya que, durante el transcurso del ensayo el área aparente de contacto varía y, sin embargo, se conserva la proporcionalidad entre la tasa de desgaste y la carga aplicada.
representa el área real de contacto (al menos a condiciones ambiente), y que por lo tanto, éste plantea que la tasa de desgaste es proporcional a dicha área. Experimentalmente, pruebas realizadas en tribómetros del tipo pin sobre anillo, donde el pin se ha caracterizado por poseer inicialmente su cara de contacto plana, han permitido corroborar esta afirmación. Ya que, durante el transcurso del ensayo el área aparente de contacto varía y, sin embargo, se conserva la proporcionalidad entre la tasa de desgaste y la carga aplicada. - La tasa de desgaste es independiente de la velocidad de deslizamiento siempre y cuando se demuestre que la presión de flujo plástico y el factor K permanecen constantes: esto se deduce del modelo planteado al derivar con respecto al tiempo la expresión 15; mas para confirmar la veracidad de esta afirmación se tienen que emplear pares de materiales cuyas propiedades mecánicas sean térmicamente muy estables, por lo menos al interior de un buen intervalo de sus condiciones de trabajo. Archard no discute sobre la validez de esta afirmación ya que no posee evidencia experimental.
- El valor teórico de la tasa de desgaste es independiente del modelo usado para representar las superficies: El modelo propuesto sustituye la concepción del modelo de Holm sobre el desgaste como un proceso de remoción de átomos mediante encuentros entre átomos. Archard rechaza este modelo, a pesar de que en él se muestra la proporcionalidad entre la tasa de desgaste y la carga normal, debido a la falta de evidencia experimental (a juicio de los autores se considera que actualmente esta visión del proceso de desgaste debe retomarse a la luz de la nanotribología y buscar un modelo que permita llevar los resultados obtenidos por este camino a la escala de trabajo convencional). Además, muestra que la modificación que Holm propone para su modelo, al considerar el material desgastado como capas atómicas removidas, no se ajusta bien a los resultados experimentales, pues para hacerlo, se debe suponer que tanto el tamaño promedio de las áreas de contacto como el de las partículas de desgaste permanece constante al incrementar la carga. De esta manera, Archard concluye que el mecanismo de remoción por grumos mediante deformación plástica involucrado en su modelo, es el que mejor explica los resultados experimentales y como se mostró antes, en él no es necesario suponer un modelo para la distribución de las alturas de las aspereza. Por otro lado, hace notar que aunque el modelo de Burwell & Strang se ajusta bien con los resultados experimentales, no es necesario asumir que los tamaños promedio de las áreas de contacto y de las partículas de desgaste permanecen constantes. En este modelo, el desgaste se concibe también como remoción de grumos a partir de los contactos entre las asperezas.
La interpretación del factor de probabilidad K, como un valor que hace referencia a la fracción de contactos que conllevan a la transferencia o formación de partículas de desgaste, debe ser tenida en cuenta con cierta reserva, pues este valor se ve altamente influenciado por el tamaño de las partículas de desgaste y su cantidad. Así, un valor de K pequeño no necesariamente significa que una pequeña fracción de los contactos ocurridos durante el deslizamiento permitían la formación de partículas de desgaste, pues el número de estas partículas puede ser muy alto y su tamaño muy reducido. El caso contrario también es posible. El factor K debe ser visto como un indicador de la reducción de la transferencia o del desgaste con respecto a un valor máximo esperado (caso en el cual en cada contacto se genere una partícula de desgaste) y de esta manera constituye un parámetro de valoración o estimación de los resultados experimentales.
4.5 VISUALIZACIÓN Y USO DEL MODELO
El modelo puede visualizarse a través de la expresión matemática 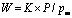 y su uso se restringe a aquellos casos en los cuales el comportamiento exhibido por un tribosistema sea estable en el tiempo y no presente fluctuaciones. Su aplicación se extiende también a algunos sistemas lubricados donde el lubricante sea una sustancia inerte. Los cambios presentados en los valores de K para un tribosistema en particular pueden ser útiles para identificar cambios en los mecanismos de desgaste. Otro uso posible del factor K es la clasificación de sistemas para distintas aplicaciones tribológicas, o simplemente para determinar que sistemas pueden emplearse en una aplicación en particular.
y su uso se restringe a aquellos casos en los cuales el comportamiento exhibido por un tribosistema sea estable en el tiempo y no presente fluctuaciones. Su aplicación se extiende también a algunos sistemas lubricados donde el lubricante sea una sustancia inerte. Los cambios presentados en los valores de K para un tribosistema en particular pueden ser útiles para identificar cambios en los mecanismos de desgaste. Otro uso posible del factor K es la clasificación de sistemas para distintas aplicaciones tribológicas, o simplemente para determinar que sistemas pueden emplearse en una aplicación en particular.
5. COMENTARIOS A LOS DOS MODE-LOS PROPUESTOS POR ARCHARD
Con base en los numerales anteriores, se procede a continuación a realizar una serie de comentarios sobre diversos aspectos de los modelos considerados, el modelo para la topografía superficial y el modelo de desgaste mecánico propuestos por Archard. Algunos de estos comentarios sirven para complementar el modelo de desgaste estudiado hasta el momento y pueden ser vistos como aquella retroalimentación mostrada en la carta de flujo, propuesta en el método de Ashby.
Trabajos posteriores realizados por Archard sobre la influencia de la topografía superficial en las relaciones entre la carga y el área real de contacto, consideran varios órdenes de estructuras de imperfecciones superficiales (hasta tres órdenes de asperezas que se hallan sobre asperezas más grandes y así sucesivamente hasta llegar a las ondulaciones) y logran mostrar teóricamente, bajo el supuesto de que las asperezas se hallan deformadas elásticamente, como la relación carga – área real de contacto tiende a ser lineal al incrementar los órdenes de imperfecciones. De esta manera, al representarse de una forma más real la topografía superficial, la relación carga – área real de contacto se convierte en lineal e independiente del estado de deformación, plástico y/o elástico. Esto se explica porque la presencia de contactos múltiples de naturaleza elástica de diversos órdenes tiende a ser lineal y al comportamiento invariable exhibido por uno o varios contactos plásticos. Lo anterior muestra claramente como el comportamiento elástico exhibido por grupos de asperezas se diferencia notablemente del comportamiento de una sola (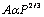 ).
).
Greenwood y Williamson[6] (G&W) investigaron la naturaleza de los contactos entre superficies nominalmente planas, suponiendo en sus estudios teóricos que las alturas de las asperezas tienen una distribución exponencial o gaussiana (siendo esta última la más representativa); ambas distribuciones se ajustan bastante bien con las mediciones realizadas por ellos y otros investigadores a diversas superficies. En su trabajo sobre contactos elásticos se muestra claramente la independencia entre el área real de contacto y el área nominal. El área real de contacto es una función lineal (o casi lineal) de la carga normal aplicada. Además, el tamaño promedio de los contactos depende muy poco de la carga, lo cual se ajusta bien con el supuesto hecho por Bowden, Tabor, Holm, Strang y Burwell. Por su parte, la presión promedio en los contactos depende poco de la carga normal y permanece casi constante al variar la carga; mientras que el número de contactos aumenta prácticamente de manera proporcional a ésta. Esto permitió a G&W desarrollar el concepto de dureza elástica, en analogía con la dureza convencional asociada con una deformación plástica. La dureza elástica se define como 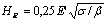 , al menos para superficies que posean asperezas cuyas alturas se distribuyan según una distribución gaussiana. En esta expresión E es el módulo de elasticidad reducido, es la raíz cuadrada de las medias de las desviaciones normales de las distribuciones de alturas de las dos superficies y
, al menos para superficies que posean asperezas cuyas alturas se distribuyan según una distribución gaussiana. En esta expresión E es el módulo de elasticidad reducido, es la raíz cuadrada de las medias de las desviaciones normales de las distribuciones de alturas de las dos superficies y 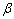 es el radio de curvatura promedio de las asperezas. Del modelo inicial propuesto por Archard para representar las superficies y estudiar contactos múltiples, se puede advertir de manera muy intuitiva esta relación, ya que como se mostró, también existe una relación casi lineal entre el área real de contacto y la carga normal para el caso de una superficie donde la altura de sus asperezas se distribuye uniformemente en la profundidad y los contactos son de tipo elástico. El análisis hecho por Archard en su modelo de desgaste, aceptando el mecanismo de remoción por grumos procedentes de una región deformada plásticamente, le permite concluir que no es necesario que el tamaño promedio de los contactos permanezca constante para el resultado obtenido y que por lo tanto, un modelo desgaste no necesita suponer esta hipótesis. Sin embargo, el trabajo de G&W muestra que aunque no sea necesaria esta hipótesis (al menos para corroborar el mecanismo de desgaste propuesto por Archard), existe un balance entre la carga normal aplicada, el número de contactos y el tamaño promedio de éstos; al incrementar la carga, los contactos existentes se hacen más grandes, mas los nuevos contactos son pequeños y permiten mantener invariable el tamaño promedio de todos.
es el radio de curvatura promedio de las asperezas. Del modelo inicial propuesto por Archard para representar las superficies y estudiar contactos múltiples, se puede advertir de manera muy intuitiva esta relación, ya que como se mostró, también existe una relación casi lineal entre el área real de contacto y la carga normal para el caso de una superficie donde la altura de sus asperezas se distribuye uniformemente en la profundidad y los contactos son de tipo elástico. El análisis hecho por Archard en su modelo de desgaste, aceptando el mecanismo de remoción por grumos procedentes de una región deformada plásticamente, le permite concluir que no es necesario que el tamaño promedio de los contactos permanezca constante para el resultado obtenido y que por lo tanto, un modelo desgaste no necesita suponer esta hipótesis. Sin embargo, el trabajo de G&W muestra que aunque no sea necesaria esta hipótesis (al menos para corroborar el mecanismo de desgaste propuesto por Archard), existe un balance entre la carga normal aplicada, el número de contactos y el tamaño promedio de éstos; al incrementar la carga, los contactos existentes se hacen más grandes, mas los nuevos contactos son pequeños y permiten mantener invariable el tamaño promedio de todos.
Aunque Archard visualizó una relación entre el comportamiento elástico y plástico de los materiales no logró determinarla cuantitativamente.
A partir de este nuevo concepto de dureza elástica y haciendo uso de su modelo propuesto para representar las superficies, G&W logran construir un criterio que permite determinar si un par de superficies en contacto exhiben un comportamiento predominantemente elástico o plástico de manera casi independiente de la carga normal que se le aplique. Este criterio se basa en el uso de un índice de plasticidad definido como 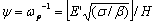 , donde H es la dureza de la superficie más blanda (ya que en ésta se inicia el flujo plástico), y las otras variables son las definidas antes para la dureza elástica. Se observa que este índice establece una relación entre las durezas elástica y plástica de las superficies en contacto, e involucra tres propiedades del material y dos parámetros que definen la topografía de las superficies. En teoría se pueden establecer criterios que comprometen la relación entre la fracción del área total de contacto (A) que se encuentra plásticamente deformada (Ap) y el índice de plasticidad
, donde H es la dureza de la superficie más blanda (ya que en ésta se inicia el flujo plástico), y las otras variables son las definidas antes para la dureza elástica. Se observa que este índice establece una relación entre las durezas elástica y plástica de las superficies en contacto, e involucra tres propiedades del material y dos parámetros que definen la topografía de las superficies. En teoría se pueden establecer criterios que comprometen la relación entre la fracción del área total de contacto (A) que se encuentra plásticamente deformada (Ap) y el índice de plasticidad 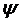 , para determinar si la superficie como tal se comporta (en su mayoría) de manera elástica o plástica. En teoría,
, para determinar si la superficie como tal se comporta (en su mayoría) de manera elástica o plástica. En teoría, 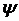 puede variar desde cero hasta un valor infinito, pero a nivel práctico se encuentra que este varía desde 0,1 hasta unas centenas. En este intervalo de variación se tiene que, solamente para valores de
puede variar desde cero hasta un valor infinito, pero a nivel práctico se encuentra que este varía desde 0,1 hasta unas centenas. En este intervalo de variación se tiene que, solamente para valores de 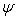 entre 0,6 y 1, la información sobre el modo de deformación gobernante se hace dudosa y por lo tanto, a partir de este resultado se ha establecido el siguiente criterio: para un valor de
entre 0,6 y 1, la información sobre el modo de deformación gobernante se hace dudosa y por lo tanto, a partir de este resultado se ha establecido el siguiente criterio: para un valor de 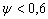 las superficies se comportan de manera elástica, mientras que para
las superficies se comportan de manera elástica, mientras que para 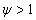 , éstas se comportan plásticamente; para valores del índice de plasticidad entre 0,6 y 1 se tiene un estado de deformación combinado elástico-plástico.
, éstas se comportan plásticamente; para valores del índice de plasticidad entre 0,6 y 1 se tiene un estado de deformación combinado elástico-plástico.
Un resultado importante, que ha surgido del empleo del índice de plasticidad para definir el comportamiento de superficies reales comunes en aplicaciones de ingeniería, muestra que la mayoría de estas superficies se comportan de manera plástica y que las superficies que exhiben comportamientos elásticos son poco comunes ya que requieren de procesos de fabricación muy elaborados que permitan reducir las rugosidades medias cuadráticas e incrementar los radios de curvatura. También, superficies con valores de estos parámetros topográficos relativamente elevados pueden comportarse elásticamente si poseen valores de dureza muy elevados. Todo esto reafirma el supuesto hecho por Archard y otros investigadores como Bowden y Tabor acerca de las asperezas deformadas plásticamente a nivel de los contactos íntimos entre éstas, permitiendo confirmar la validez respecto a estos supuestos en los diferentes modelos (de fricción y desgaste) así elaborados. Por su parte K.L. Jonson[7] y otros investigadores con base en sus observaciones y en estudios efectuados a partir de la teoría de la plasticidad y de los teoremas de Amortiguamiento o Shakedown, plantean un mecanismo de desgaste basado en la acumulación unidireccional de una deformación plástica en los contactos debida a sus constantes interacciones producto del deslizamiento entre las superficies. A este mecanismo se le conoce como ratchetting en la literatura y permite vislumbrar de una manera más profunda y detallada el mecanismo de remoción por grumos propuesto por Archard.
A pesar de que el modelo de G&W es un modelo muy elaborado y más próximo a las condiciones reales en que trabaja una superficie, los mecanismos asumidos por Archard y los resultados obtenidos son aceptables y consistentes como se ha mostrado anteriormente. Sin embargo, existen dudas con respecto al tipo de distribución asumida para las alturas de las asperezas en las superficies rugosas; pues si bien él comenta que lo hace con base en una pequeña evidencia que posee, no hace mención específica de ésta.
Existe una característica común en la formulación de Archard para sus dos modelos: se asume una independencia total entre los mecanismos involucrados en cada modelo. Estos mecanismos se tratan por separado y luego se hacen consideraciones sobre su importancia para obtener un modelo general resultante de la suma de ellos que, para el caso del modelo de desgaste, resulta en la consideración de un sólo mecanismo al final, en vez de los cuatro planteados inicialmente. Por otro lado, el modelo de G&W involucra de manera simultánea los dos mecanismos de deformación, tal y como sucede en una situación real. Para el estudio del desgaste y del contacto se considera que la forma correcta de construir un modelo general, debe considerar la actuación simultánea y dependiente de los diversos mecanismos presentes.
A pesar de que el autor considera de forma separada los dos regímenes de deformación, es posible considerar una secuencia de eventos en los cuales el material pasa de una condición elástica a una plástica evidenciando un proceso de acomodamiento asociado a la primera condición, conocido en tribología como running-in.
Un aspecto de importancia a rescatar de la discusión hecha por Archard, es la existencia de varios niveles de estructuras de imperfecciones y, aunque en su trabajo solamente utilizó el nivel de las asperezas para consolidar sus modelos, se debe considerar que las áreas de influencia asociadas con las crestas o colinas de las ondulaciones, constituyen sitios preferenciales para que interactúen las asperezas de ambas superficies. Como resultado de estas interacciones, las asperezas se deforman plásticamente en su gran mayoría, lo que posibilita la aparición de un mecanismo de desgaste por remoción de grumos a la manera propuesta por Archard y mejorada por Johnson; sin embargo, a nivel de las ondulaciones donde se hallan estas asperezas, se generan campos elásticos de esfuerzos, los cuales varían constantemente en el espacio y en el tiempo posibilitando de esta manera la activación de un mecanismo de fatiga a esta escala, que quizás sea el responsable de las partículas de desgaste de gran tamaño con forma de plaquitas que se observan a menudo. De esta forma, el modelo propuesto por Archard, podría modificarse un poco empleando sus resultados para los dos mecanismos de remoción por grumos, de la siguiente manera:
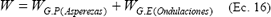
Nuevamente, al suponer partículas de desgaste de forma hemisféricas y teniendo presente que a representa el radio de la zona de contacto o de influencia en cada caso, se tiene que 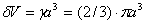 , de donde
, de donde 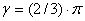 ; y por lo tanto, las dos expresiones anteriores deducidas para la tasa de desgaste se transforman en
; y por lo tanto, las dos expresiones anteriores deducidas para la tasa de desgaste se transforman en
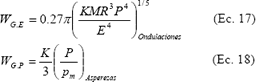
Para el mecanismo de remoción a nivel de las ondulaciones se hacen los siguientes comentarios:
- M representa una densidad de las asperezas con respecto a la profundidad y puede redefinirse empleando el modelo G&W para obtener una expresión para ésta más ajustada a la realidad.
- R representa el radio promedio de las cimas de las ondulaciones.
- K en este caso puede relacionarse con la probabilidad de generar una partícula de desgaste a partir del contacto macro generado en una zona de influencia; este factor se puede relacionar con el número de interacciones necesarias para generar tal partícula a la manera como lo hizo Kragelskii[8].
- Se asume este mecanismo de remoción por grumos y no por capas, debido a que por su origen elástico, el tamaño de las partículas, que se halla relacionado con el área superficial de los macro-contactos
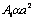 y con la profundidad (o espesor) de una capa crítica, la cual a su vez está relacionada con el radio de las zonas de influencia
y con la profundidad (o espesor) de una capa crítica, la cual a su vez está relacionada con el radio de las zonas de influencia 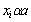 , termina siendo una función que depende del cubo de dicho radio. Esto se debe a que en un contacto hertziano, la profundidad de máximo esfuerzo se puede relacionar con el tamaño del contacto caracterizado por su radio o semiancho.
, termina siendo una función que depende del cubo de dicho radio. Esto se debe a que en un contacto hertziano, la profundidad de máximo esfuerzo se puede relacionar con el tamaño del contacto caracterizado por su radio o semiancho.
K.L. Jonson[7] al tratar de aproximarse al fenómeno del desgaste desde la mecánica del contacto propone la presencia del mecanismo de ratchetting asociado a la acumulación cíclica unidireccional de la deformación plástica paralela a la superficie, que compite con un mecanismo de fatiga de bajo ciclaje asociado con los esfuerzos y deformaciones normales a la superficie. Dependiendo de las amplitudes de las deformaciones asociadas en cada caso, uno de estos mecanismos será el que determine el origen del desprendimiento de la partícula de desgaste. Al considerar la escala de las asperezas, parece ser que con base en las distintas hipótesis realizadas, el mecanismo que se impone es el del ratchetting. Al considerar la escala de las ondulaciones, y en especial las zonas correspondientes a las cimas de éstas, es muy probable que allí las deformaciones sean de tipo elástico. Además, al considerar el principio de Saint Venant, los esfuerzos y deformaciones generados resultan ser menos críticos que los presentes a nivel de las asperezas, y por lo tanto, un mecanismo de fatiga de alto ciclaje puede encontrarse operando. El número de ciclos necesarios para producir el desprendimiento de una partícula a este nivel (una partícula mucho más grande que las provenientes de las asperezas) puede alcanzarse rápidamente considerando la cantidad de interacciones que ocurren por unidad de tiempo o de longitud. Es a este mecanismo al cual se asocia, la componente propuesta para el modelo de Archard en las expresiones 24 y 25.
6. EFECTO DE LA TEMPERATURA
Con respecto a las propiedades mecánicas que aparecen en estos modelos, debe considerarse el efecto que sobre éstas pueden ejercer la temperatura y los posibles cambios microestructurales que puedan ocurrir bajo diversas condiciones de carga, velocidad y ambiente. Aunque en el modelo de Archard, se supone un estado estable (independiente del tiempo), y en el cual los efectos de la temperatura son despreciables (se observa que para las estimaciones del factor K se emplean valores de la dureza de los materiales a temperatura ambiente), la realidad está bastante lejos de esto. Trabajos desarrollados por Bowden y Tabor[5] y por otros investigadores[9,10] muestran cómo las temperaturas promedio en la superficie y a nivel de las asperezas son lo suficientemente elevadas como para modificar drásticamente las propiedades mecánicas de manera localizada y desencadenar transformaciones de fase mediante mecanismos termo-mecánicos. El trabajo experimental de Prasad[9], sobre la influencia de la naturaleza de los micro-constituyentes y las condiciones de deslizamiento en el desgaste por deslizamiento en seco exhibido por cuatro aleaciones empleadas para cojinetes, muestra cómo existen grandes variaciones en las propiedades mecánicas tales como la dureza, la resistencia tensil y compresiva entre otras, debido al calentamiento causado por la fricción a nivel de la intercara deslizante. Esto hace las propiedades mecánicas medidas a temperatura ambiente sean aplicables sólo en aquellos modelos en los que los incrementos de temperatura sean bajos, o donde los materiales empleados posean una alta estabilidad térmica que evite la variación de sus propiedades mecánicas.
Con base en las mediciones de dureza en caliente efectuadas por Blaz & Nowotnik[12] en su trabajo sobre la deformación a alta temperatura de una aleación Cu-Al, en el presente trabajo se ha hecho uso de estos datos y se han reconstruido algunas de las curvas allí presentadas, donde se muestra el efecto de la temperatura y la tasa de deformación en la dureza de una aleación de Cu-8wt%Al deformada en caliente. Con base en estas curvas y empleando dos regresiones diferentes, se han encontrado expresiones útiles para estimar la dureza de la aleación considerada en un rango de temperaturas, para el cual, los cambios microestructurales son poco significativos. A continuación se muestran los resultados de este pequeño estudio.
En la Figura 5 se muestran los resultados de las mediciones de dureza efectuadas por Blaz & Nowotnik para diversas temperaturas y dos tasas de deformación diferentes. Para esta aleación se observa una disminución de la dureza al incrementarse la temperatura hasta alcanzar un valor mínimo y un incremento al aumentar la tasa de deformación. Este último aspecto también debería ser considerado en un modelo de desgaste ya que por lo general, las tasas de deformación allí presentes son muy altas en comparación con las que se manejan en los ensayos típicos de dureza y de tracción. Con base en los datos consignados en esta figura se ha hecho uso del modelo propuesto por Westbrook[8] para metales y algunas aleaciones, en el cual se establece una relación para la dureza y la temperatura definida por la expresión 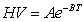 donde HV es la dureza Vickers, T es la temperatura en grados Kelvin y A y B son un par de constantes. Debe resaltarse el hecho, de que ambas constantes tienen un significado físico y no son meramente números que permiten asegurar una correlación buena entre un grupo datos medidos.
donde HV es la dureza Vickers, T es la temperatura en grados Kelvin y A y B son un par de constantes. Debe resaltarse el hecho, de que ambas constantes tienen un significado físico y no son meramente números que permiten asegurar una correlación buena entre un grupo datos medidos.
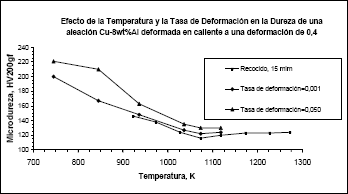
Figura 5. Resultados de los trabajos efectuados por Blaz y Nowotnik[12]
Figure 5 Results of the works conducted by Blaz and Nowotnik
La constante A representa la dureza intrínseca del metal, o sea, su dureza a 0 K, y podría representar una medida de la resistencia inherente de las fuerzas de unión de las redes. Por su parte, la constante B define el coeficiente de temperatura de la dureza y ha sido relacionada con el cambio en el contenido de calor con el incremento de la temperatura (Ver referencia 12, quizás esto se refiera mejor al cambio en la energía interna en función de la temperatura).
Los resultados de las correlaciones obtenidas al emplear la ecuación de Westbrook (Ver figura 6) confirman una vez más que este modelo permite establecer una buena relación de dependencia entre la temperatura y la dureza de la aleación de cobre aluminio para las dos tasas de deformación.
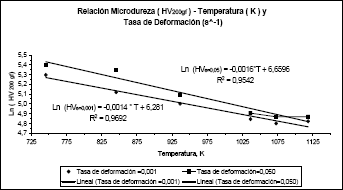
Figura 6. Relación Microdureza, Temperatura y Tasa de Deformación según el modelo de Westbrook[13] aplicado a los datos de la Figura 4.
Figure 6 Relation Micro-hardness, Temperature and Rate of Deformation according to the model of Westbrook applied to the data of figure 4.
Por otro lado, en el presente trabajo se propone otra expresión que permite relacionar la temperatura y la dureza, la cual tiene la forma 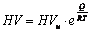 donde nuevamente HV es la dureza Vickers y T es la temperatura en grados Kelvin. es un valor límite de la dureza a elevadas temperaturas, Q es una energía de degradación de la propiedad medida, en este caso la dureza, y puede estar relacionada con los procesos de restauración de la estructura cristalina debido al ablandamiento producido por aparición de nuevos granos libres de deformaciones y a los movimientos de relajación y desaparición de muchas dislocaciones. La constante R es la constante de los gases y tiene un valor de
donde nuevamente HV es la dureza Vickers y T es la temperatura en grados Kelvin. es un valor límite de la dureza a elevadas temperaturas, Q es una energía de degradación de la propiedad medida, en este caso la dureza, y puede estar relacionada con los procesos de restauración de la estructura cristalina debido al ablandamiento producido por aparición de nuevos granos libres de deformaciones y a los movimientos de relajación y desaparición de muchas dislocaciones. La constante R es la constante de los gases y tiene un valor de 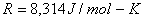 . Nuevamente las constantes de esta relación tienen una interpretación física, sólo basta efectuar una serie de estudios más detallados que permitan validar mejor este modelo.
. Nuevamente las constantes de esta relación tienen una interpretación física, sólo basta efectuar una serie de estudios más detallados que permitan validar mejor este modelo.
Los resultados obtenidos al emplear esta relación se muestran en la Figura 7, donde se observa que son bastante aceptables y que las correlaciones son del mismo orden que las obtenidas con la ecuación de Westbrook. De esta manera, ambos modelos podrían complementarse y definir un intervalo para los valores posibles de la dureza en función de la temperatura siempre y cuando no existan cambios microestructurales que modifiquen drásticamente el comportamiento de los materiales. Por otro lado, estos resultados pueden dar información valiosa sobre la dirección en que ocurre la transferencia de material metálico entre las superficies; también permitiría predecir cuál es la superficie en la que predomina el desgaste, al analizar un par de superficies en contacto y deslizando entre sí. Estas tendencias o cambios se pueden identificar inicialmente mediante una evaluación de los valores relativos de dureza a las condiciones de trabajo, valores que pueden incluso dar información sobre los mecanismos operantes.
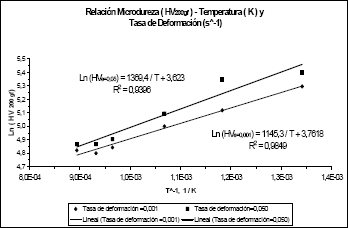
Figura 7. Relación Microdureza, Temperatura y Tasa de Deformación según el modelo sugerido por Suárez[14], aplicado a los datos de la Figura 4.
Figure 7. Relation Micro-hardness, Temperature and Rate of Deformation according to the model suggested by Suárez, applied to the data of figure 4.
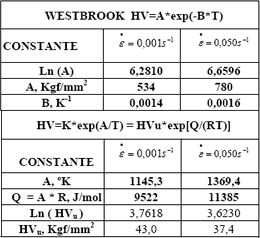
En la Tabla 3 se hace un resumen de los valores de las constantes involucradas en estos modelos. Con base en los resultados obtenidos del modelo de Westbrook se observa que existe una influencia marcada de la tasa de deformación en los valores de dureza intrínseca del material, en especial en la medida en que la temperatura es menor. A medida que la temperatura aumenta su influencia es menos marcada y esto se debe al valor mayor que presenta el coeficiente de temperatura para la tasa de deformación más alta. De esta manera, es de esperar que para valores muy altos de temperatura, la influencia de la tasa de deformación sea casi nula. Esta última observación se advierte en los resultados mostrados por el modelo propuesto en este trabajo, en el cual se muestra que para valores de temperatura muy altos, la dureza tiende a estabilizarse alrededor de unos 40 Kgf/mm independientemente de la tasa de deformación. Nuevamente, el valor de la energía de degradación Q, muestra como a medida que la temperatura disminuye, el efecto de la tasa de deformación en la dureza es mayor.
Tabla 3. Resumen de los valores de las constantes determinados con base en los dos modelos empleados.
Table 3- Summary of the values of the constants determined with used models.
7. CONCLUSIONES
La aplicación del método propuesto por Ashby para el modelamiento de problemas físicos, ha sido una herramienta fundamental en el análisis de los modelos propuestos por Archard (Modelo de contactos múltiples en superficies rugosas y modelo de desgaste mecánico). Con base en este método se ha podido realizar un análisis más profundo de lo convencional a dichos modelos, y en especial, mostrar mediante este trabajo un panorama mucho más amplio del modelo clásico de desgaste de Archard, aspecto que no es mostrado con frecuencia en los textos y artículos de tribología, donde el tratamiento dado a este modelo resulta ser muy superficial y las críticas que se le hacen son de todo tipo y a menudo parece que desconocieran las limitaciones que tuvo este investigador en su época y su propia visión (futura) sobre los aspectos que deberían considerarse en un modelo de desgaste.
La introducción de ecuaciones constitutivas que describan el comportamiento de los materiales de los cuerpos en contacto en función de la temperatura, las deformaciones aplicadas, la tasa de deformación y sus propiedades mecánicas y térmicas constituye un elemento de suma importancia que debe involucrarse al interior de los modelos de desgaste.
Con los resultados de este pequeño trabajo, se pretendió mostrar un método mediante el cual sea posible construir una serie de ecuaciones constitutivas para los materiales en contacto y que puedan ser empleadas para predecir el comportamiento a desgaste exhibido por las superficies de un par de cuerpos en contacto deslizante. Para estimar el valor de la temperatura promedio en la superficie o a nivel de las asperezas, se puede hacer uso de los modelos propuestos por Bowden y Tabor e incluso por otros mejorados que pueden consultarse en varias referencias[11, 12].
Con base en las expresiones de modelos que permiten estimar la temperatura para unas condiciones de operación determinadas, es posible integrar al modelo de desgaste el coeficiente de fricción ya que el incremento en la temperatura resulta ser proporcional a dicho coeficiente. Por otro lado, para el mecanismo de desgaste propuesto a nivel de las ondulaciones es posible incluir el coeficiente de fricción en el proceso de ratchetting, debido a que son las cargas que traccionan las superficies, quienes en principio generan las deformaciones tangenciales a nivel de la superficie y sus proximidades.
Con base en los mecanismos de desgaste actualmente aceptados a nivel mundial[15, 16], se puede observar que los mecanismos de desgaste aquí propuestos, corresponden básicamente a mecanismos dominados por deformación plástica. En el caso de la remoción por grumos opera un mecanismo de tipo adhesivo y a un mecanismo de fatiga a nivel superficial asociado con el ratchetting. A nivel de las ondulaciones el mecanismo operante puede ser un mecanismo de fatiga de alto ciclaje.
REFERENCIAS [ Links ][2]














