Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
DYNA
versão impressa ISSN 0012-7353versão On-line ISSN 2346-2183
Dyna rev.fac.nac.minas v.72 n.147 Medellín set./dez. 2005
MODELADO DEL INDICE DE PRECIOS AL CONSUMIDOR USANDO UN MODELO HIBRIDO BASADO EN REDES NEURONALES ARTIFICIALES
CONSUMER PRICE INDEX MODELLING USING AN ARTIFICIAL NEURAL NETWORKS-BASED HYBRID MODEL
JUAN DAVID VELÁSQUEZ HENAO
Escuela de Sistemas, Facultad de Minas, Universidad Nacional de Colombia
SANTIAGO FERNANDO MONTOYA MORENO
Escuela de Sistemas, Facultad de Minas, Universidad Nacional de Colombia
Recibido para revisión 6 de Agosto de 2004, aceptado 11 de Octubre de 2004, versión final 10 de Noviembre de 2004
RESUMEN: Un nuevo modelo híbrido es propuesto para pronosticar el índice colombiano de precios al consumidor. Este es basado en una descomposición estructural de la serie temporal con el objetivo de remover cualquier patrón fácilmente detectable en los datos, y en el uso de un perceptron multicapa para modelar las relaciones ocultas en la serie de tiempo. Los resultados superan las aproximaciones clásicas basadas en la aproximación de Box y Jenkins, y los modelos convencionales de Redes Neuronales, e incentivan el estudio de este tipo de aproximación híbrida para modelar otras series temporales.
PALABRAS CLAVE: Métodos de Pronóstico, Índice de Precios al Consumidor, Redes Neuronales Artificiales, Métodos Híbridos.
ABSTRACT: A new hybrid model is proposed to forecasting the Colombian Consumer Price Index. Its based on the structural decomposition of the original time series with the aim of remove any easily detected pattern in the data, and in the use of multilayer perceptron to model hidden relationships in the studied time series. The results overcome classical approaches based on Box-Jenkins methodology and conventional neural networks methodology, and encourage the study of this hybrid approach to modelling other time series.
KEYWORDS: forecasting methods, costumer price index, neural networks, hybrid methods.
1. INTRODUCCIÓN
El pronóstico de series temporales es un problema común a las ciencias y la ingeniería (Kasabov, 1998), tal que muchos esfuerzos han sido dedicados al desarrollo de nuevos métodos (Brown, 1963; Box y Jenkins, 1970; Harvey, 1989; Holt, 1957; Pole, West y Harrison, 1994; Winters, 1960). Mientras la aproximación clásica al modelamiento de series de tiempo considera el caso lineal (Box y Jenkins, 1970), la última década se ha caracterizado por el desarrollo de modelos paramétricos no lineales (Granger y Terasvirta, 1993; Tong, 1990). Sin embargo, la mayor crítica realizada ha estos últimos, es que asumen una forma predeterminada para la representación la no linealidad presente en la serie temporal (Granger y Terasvirta, 1993), tal que ellos no son siempre aplicables. En este contexto, las redes neuronales artificiales (Rumelhart y McClelland, 1986) (RNA) interpretadas como modelos no paramétricos y no lineales (Sarle, 1994), han sido exitosamente aplicados al modelamiento y pronóstico de series temporales no lineales (Dofner, 1996; Hansen y Nelson, 1997; Tang y Fishwick, 1993; Saad, Prokhorov y Wunsch, 1998; Westheider, 1997), cuando no hay leyes físicas o teoría económica que guíe la especificación de un modelo econométrico completamente parametrizado (Granger y Terasvirta, 1993). No obstante, su formulación no es una tarea fácil (DasGupta, Siegelmann y Sontag, 1995; Kaastra y Boyd, 1996; Anders y Korn, 1999, Sontag y Sussman, 1989), y en el proceso de construcción del modelo debe tenerse especial cuidado en varios pasos críticos con el fin de obtener una adecuada representación del proceso generador de la serie temporal. Entre estos últimos, el procedimiento de remoción de características fácilmente visibles tales como tendencias, patrones estacionales o ciclos de largo plazo, juega un rol importante en el preprocesamiento de los datos (Kaastra y Boyd, 1996; Masters, 1993; Masters, 1995), que cuando es realizado inadecuadamente puede conducir a modelos que representan pobremente la serie temporal.
En este trabajo se modela y pronostica el índice colombiano de precios al consumidor (ICPC), y se muestra como el modelado directo de las características estructurales de la serie, combinado con un modelo de redes neuronales permite su representación más completa, obteniéndose así un modelo híbrido de pronóstico; esta aproximación permite la remoción óptima de las componentes estructurales de la serie temporal. Los resultados obtenidos son contrastados con la aproximación de Box y Jenkins, y un modelo convencional de redes neuronales artificiales.
El resto del artículo es organizado como sigue: la sección 2 introduce la metodología de Box y Jenkins para modelar el ICPC; la sección 3 presenta una revisión de los principales tópicos sobre el modelamiento de series temporales usando redes neuronales; la sección 4 presenta la base conceptual de la metodología propuesta, y los resultados de su aplicación a la serie del ICPC; en la sección 5, se presenta su relación con otros modelos híbridos propuestos en la literatura; finalmente, las conclusiones son presentadas en la sección 6.
2. LA APROXIMACIÓN DE BOX Y JENKINS
La serie modelada corresponde al índice mensual de precios al consumidor en Colombia para el período comprendido entre dic98 y may04 (véase la Figura 1). Los datos entre dic98 y jun03 son usados para estimar los parámetros del modelo, mientras el resto es usado para verificar la precisión del pronóstico extrapolativo doce meses adelante; esto es, el pronóstico realizado para un mes determinado es usado como entrada para predecir el mes siguiente y no el valor real.
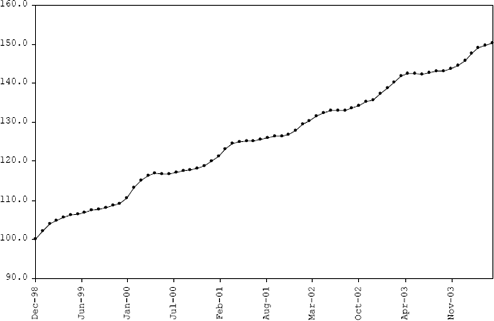
Figura 1. Índice mensual de precios al consumidor. El valor base es fijado en 100 por en Gobierno para dec98.
Figure 1. Monthly consumer price index. The base value is fixed on 100 by the government for dec98
La inspección visual de los datos revela una fuerte tendencia lineal combinada con una componente estacional asociada al año, la cual es explicada por la variación interna de la economía del país durante este lapso de tiempo. Siguiendo la metodología de Box y Jenkins, la serie temporal debe ser hecha estacionaria en el sentido homogéneo, esto es, media y varianza constantes en el tiempo; para ello, la tendencia y el patrón estacional son eliminados mediante una diferenciación de primer orden y posteriormente por una diferenciación estacional de periodo doce. Las propiedades estadísticas de la serie resultante son presentadas en
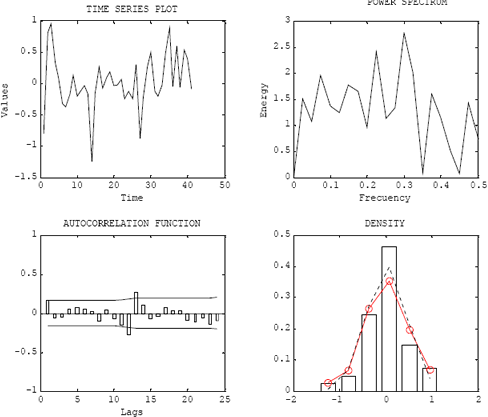
Figura 2. Propiedades estadísticas de la serie zt=(1-B)(1-B12) yt.
Figure 2. Statistical properties of the time series zt=(1-B)(1-B12) yt.
El periodograma no revela ningún componente cíclico importante; la distribución de probabilidades de los datos es realizada de forma empírica usando una aproximación no paramétrica basada en funciones núcleo; como puede observarse, los datos siguen aproximadamente una distribución normal; el autocorrelograma indica que las correlaciones para los rezagos 1, 11, 12 y 13 son significativamente diferentes de cero.
Estos hallazgos sugieren el siguiente modelo preliminar para pronosticar el ICPC, representado aquí por yt:
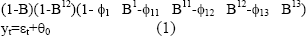
Seguidamente, todos los posibles modelos obtenidos a partir de
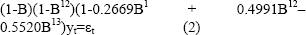
donde et es una variable aleatoria siguiendo una distribución normal con media cero y varianza 0.0884. En
3. APROXIMACIÓN TRADICIONAL A LA MODELACIÓN DE SERIES TEMPORALES USANDO REDES NEURONALES ARTIFICIALES
Las redes neuronales artificiales son sistemas conexionistas que imitan la estructura física del cerebro humano (Kosko, 1992), y han sido aplicadas exitosamente en la solución de diferentes tipos de problemas (Kasabov, 1998). De la vasta gama de modelos existentes, los perceptrones multicapa parecen ser el tipo de red neuronal más ampliamente usada (Masters, 1993), la cual ha sido empleada para resolver problemas de regresión, clasificación y series temporales. En este tipo de RNA, las neuronas son agrupadas por capas, teniéndose entonces una capa de entrada, una o más capas ocultas de procesamiento, y una capa de salida (véase
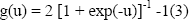
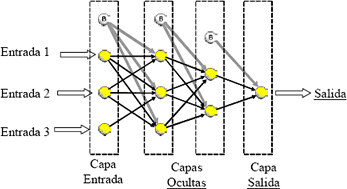
Figura 3. Perceptron multicapa con dos capas ocultas.
Figure 3. Multilayer perceptron with two hidden layers.
y la función de transferencia lineal para la activación de la neurona de la capa de salida:

De esta forma, si xit es la i-ésima componente del vector de regresores de la serie temporal en el instante t, xt, la propagación de la señal a través de un perceptron multicapa con una sola capa oculta puede representarse matricialmente como:
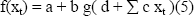
donde a representa el valor de la conexión de la neurona adaptativa a la neurona de salida, b es la matriz de pesos de las conexiones de la capa oculta a la capa de salida; d es el vector de pesos de las conexiones de la neurona adaptativa a las neuronas de la capa oculta; y finalmente c es la matriz de pesos de las conexiones de la capa de entrada a la capa oculta.
Kaastra y Boyd (1996) indican que el proceso práctico de construcción de modelos para series temporales financieras usando RNA, requieren que el pronosticador tome decisiones críticas sobre un gran número de parámetros y procesos. En consecuencia, la complejidad del proceso parece desviar la atención del modelador hacia decisiones concernientes a la selección final del modelo, para este caso particular especificado por
El proceso de selección de modelos en RNA consiste en determinar su arquitectura final (Anders y Korn, 1999), esto es, las entradas óptimas al modelo, el número de neuronas ocultas, y los valores de pesos asociados a las diferentes conexiones en la red. La metodología usada para obtener la red neuronal final es presentada a continuación.
En el modelado de series temporales, el preprocesamiento de los datos tiene el objetivo de eliminar cualquier patrón fácilmente identificable (Masters, 1995), permitiendo a
De acuerdo con las indicaciones de Smauoi et al (2002), las entradas a
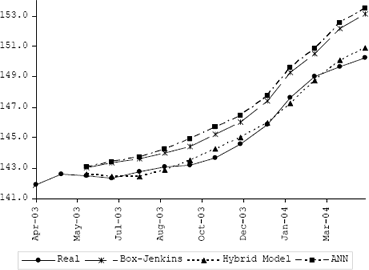
Figure 4. Pronóstico extrapolativo 12 meses hacia delante para los diferentes modelos considerados.
Figure 4. Extrapolative forecast 12 months ahead for different models
4. EL MODELO PROPUESTO
En nuestra metodología, se muestra como el modelamiento estructural de características fácilmente identificables permite obtener modelos que capturan mejor las propiedades de la serie de tiempo estudiada. Como se discutió en la sección 2, la serie del ICPC presenta una tendencia lineal y un patrón estacional anual; así, se plantea el siguiente modelo estructural preliminar:
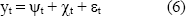
donde yt representa la tendencia lineal, y ct el patrón estacional anual. En

mientras que los componentes cíclicos son representados como la combinación de dos ondas seno con períodos de 6 y 12 meses respectivamente:
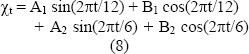
El análisis de la serie de residuos de
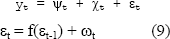
Todos los parámetros de las Ecs. (6), (7), (8) y (9) son estimados simultáneamente. El error cuadrático medio obtenido durante la estimación de los parámetros es 0.0644, y 0.1444 para el pronóstico extrapolativo doce meses adelante. El error medio porcentual absoluto fue del 0.15% en la estimación y 0.23% en el pronóstico extrapolativo.
5. RELACIÓN CON OTROS TRABAJOS
El concepto empleado para desarrollar nuestra aproximación, es usado en el modelado estructural de series temporales (Harvey, 1989; Pole et al, 1994) donde dichas propiedades estructurales representadas explícitamente en el marco de los modelos dinámicos, permitiendo que ellas cambien en el tiempo; en estos modelos, igualmente solo se considera la influencia de variables explicativas las cuales son incorporadas al modelo a través de su combinación lineal. En este trabajo se usa una aproximación diferente: el modelo propuesto es estático, tal que los valores de sus parámetros no cambian sobre el tiempo; igualmente, se modela explícitamente relaciones estáticas no lineales entre las variables a través del modelo de redes neuronales artificiales.
Zhang (2003) propone el uso de la metodología de Box y Jenkins para modelar la serie en estudio, y posteriormente, usar un modelo neuronal para pronosticar la serie de tiempo de los errores. En esta aproximación, ambas series son modeladas independientemente. En nuestra metodología, se usa un modelamiento directo de las características estructurales de la serie temporal combinado con el perceptron multicapa, tal que todos los parámetros son estimados simultáneamente.
6. ANOTACIONES FINALES
Un nuevo modelo híbrido para el modelamiento de series de tiempo es presentado. Este es basado en el modelamiento de las características estructurales particulares de la serie estudiada, tales como la tendencia, los patrones estacionales y los ciclos de largo plazo; y en el uso de RNA para representar relaciones no lineales en los datos. Su aplicabilidad es demostrada modelando la serie del ICPC. Los resultados muestran como el modelo propuesto captura de una mejor manera las propiedades de largo plazo de dicha serie de tiempo. Mientras que el modelo autoregresivo obtenido y el perceptron multicapa no tienen una diferencia significativa, nuestra aproximación reduce el error medio absoluto porcentual en el pronóstico extrapolativo del 1% al 0.23%.
7. REFERENCIAS
[1] ANDERS, U. y KORN, O. (1999), `Model selection in neural networks', Neural Networks 12(1999), 309-323. [ Links ]
[2] BOX, G. E. P. y JENKINS, G. M. (1970), Time Series Analysis: Forecasting and Control, Holden-Day Inc. [ Links ]
[3] BROWN, G. R. (1963), Smoothing, Forecasting and Prediction, Englewood Cliffs: Prentice Hall. [ Links ]
[4] DASGUPTA, B., SIEGELMANN, H. T. y SONTAG, E. D. (1995), `On the complexity of training neural networks with continuous activation functions', IEEE Transactions on Neural Networks 6(6) [ Links ]
[5] DOFNER, G. (1996), `Neural network for time series processing', Neural Networks World (4), 447-468. [ Links ]
[6] EFRON, B. y TIBSHIRANI, R. J. (1993), An Introduction to the Bootstrap, Chapman & Hall. [ Links ]
[7] GRANGER, C. W. J. y TERÄSVIRTA, T. (1993), Modeling Nonlinear Economic Relationships, Oxford University Press. [ Links ]
[8] HANSEN, J. V. y NELSON., R. D. (1997), `Neural network and time series methods: A synergic combination in state economic forecasts', IEEE Trans on Neural Networks [ Links ]
[9] HARVEY, A. C. (1989), Forecasting, structural time series models and the Kalman Filter., Cambridge University Press. [ Links ]
[10] HOLT, C. C. (1957), Forecasting seasonals and trends by exponentially weighted moving averages, in ONR Research Memorandum, number 52, Carnegie Institute of Technology, Pittsburgh, Pennsylvania. [ Links ]
[11] KAASTRA, I. y BOYD, M. (1996), `Designing a neural network for forecasting Financial and economic series', Neurocomputing (10), 215-236. [ Links ]
[12] KASABOV, N. (1998), Foundations of Neural Networks, Fuzzy Systems, and Knowledge Engineering, second edn, Massachusetts Institute of Technology. [ Links ]
[13] KOSKO, B. (1992), Neural Netwoks and Fuzzy Systems: A Dynamical Approach to Machine Intelligence, Englewood Cliffs, NJ, Prentice-Hall. [ Links ]
[14] MASTERS, T. (1993), Practical Neural Network Recipes in C++, First edn, Academic Press, Inc. [ Links ]
[15] MASTERS, T. (1995), Neural, Novel and Hybrid Algorithms for Time Series Prediction, First edn, John Wiley and Sons, Inc. [ Links ]
[16] MILLS, T. C. (1993), The econometric modelling of financial time series, Cambridge Press University. [ Links ]
[17] POLE, A., WEST, M. y HARRISON, J. (1994), Applied Bayesian Forecasting and Time Series Analysis, Chapman & Hall. [ Links ]
[18] REIDMILLER, Proceedings of the IEEE Int. Conf. on NN (ICNN) San Francisco, 1993, pp. 586-591. [ Links ]
[19] RUMELHART, D. y MCCLELLAND, J. L. (1986), Parallel Distributed Processing, Explorations in the Microstructure of Cognition, Vol. 1, MIT Press, Cambridge, MA. [ Links ]
[20] SAAD, E., PROKHOROV, D. y WUNSCH, D. (1998), `Comparative study of stock trend prediction using time delay, recurrent and probabilistic neural networks', IEEE Trans. on Neural Networks 9, 1456--1470. [ Links ]
[21] SARLE, W. (1994), Neural networks and statistical models, in S. Institute, ed., Proc. of the 19th Annual SAS Users Group Int. Conference., pp. 1538–1550. [ Links ]
[22] SMAUOI, N., BUHAMRA, S. and GABR, M. (2002) A combination of Box-Jenkins Analysis and Neural Networks to Model and Predict Water Consumption in Kuwuait. IEEE 1678-1683 [ Links ]
[23] SONTAG, E. D. y SUSSMANN, H. J. (1989), `Backpropagation can give rise to spurious local minima even for networks without hidden layers', Complex Systems 3(1). [ Links ]
[24] TANG, Z. y FISHWICK, P. A. (1993), Feed-forward neural nets as models for time series forecasting., Technical report, Department of Decision & Information Sciences. University of Florida. [ Links ]
[25] TONG, H. (1990), Non-linear Time Series, a dynamical system approach, Oxford Statistical Science Series, Claredon Press Oxford. [ Links ]
[26] WESTHEIDER, O. (1997), Predicting stock index returns by means of genetically engineered neural networks, PhD thesis, University of California. [ Links ]
[27] WINTERS, P. R. (1960), Forecasting sales by exponentially weighted moving averages, Management Sciences (6), 324–342. [ Links ]
[28] ZHANG, G. P. (2003), Time series forecasting using a hybrid ARIMA and neural network model. Neurocomputing 50 159-175. [ Links ]














