Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO  Similars in Google
Similars in Google
Share
DYNA
Print version ISSN 0012-7353On-line version ISSN 2346-2183
Dyna rev.fac.nac.minas vol.73 no.149 Medellín July 2006
PRINCIPIOS TERMODINÁMICOS DE LA REFRIGERACIÓN MAGNÉTICA
PRINCIPIOS TERMODINÁMICOS DE LA REFRIGERACIÓN MAGNÉTICA
JOHN HOYOS
Grupo de Ciencia y Tecnología de los Materiales. Universidad Nacional de Colombia, jjhoyos@unal.edu.co.
FARID CHEJNE
Profesor asociado Universidad Nacional de Colombia, fchejne@unal.edu.co.
CÉSAR CHAVES
Profesor asociado Universidad Nacional de Colombia, cachaves@unal.edu.co.
JUAN VELÁSQUEZ
Ingeniero Químico. Programa Investigación y Desarrollo. Colorquímica S.A. Medellín. juanesv@epm.net.co.
ALAN HILL
Instituto de Energía y Termodinámica. Profesor Universidad Pontificia Bolivariana. iet@upb.edu.co.
Recibido para revisar 25 de Abril de 2005, aceptado 20 de Julio de 2005, versión final 14 de Marzo de 2006
RESUMEN: La Refrigeración magnética es una de las tecnologías con mayor potencial comercial debido a sus ventajas ambientales y energéticas frente a los sistemas convencionales. Este artículo presenta los aspectos termodinámicos más importantes del efecto magnetocalórico, fundamental en el estudio de las transformaciones magnéticas y el desarrollo de la refrigeración magnética. También se explican los ciclos magnéticos de Carnot, Brayton y de Regeneración Magnética Activa aplicados a la refrigeración magnética. Los ciclos de Brayton y de Regeneración Magnética Activa se emplean en aplicaciones con amplios intervalos de la temperatura de operación.
PALABRAS CLAVE: Refrigeración magnética, efecto magnetocalórico, ciclos magnéticos, materiales magnéticos, entropía magnética
ABSTRACT: Magnetic refrigeration is one of the technologies with a high commercial potential due to its environment and energetic advantages among conventional ones. The main thermodynamic aspects of the magnetocaloric effect are presented. Magnetic transformations and magnetic refrigeration technology, are based in the magnetocaloric effect. Also, the Carnot, Brayton and Magnetic Active Regeneration cycles are explained. It is important to notice that the Magnetic Active Regenerative cycle is used in applications with room temperatures.
KEY WORDS: magnetic refrigeration, magnetocaloric effect, magnetic cycles, magnetic materials, magnetic entropy
1. INTRODUCCIÓN
La refrigeración magnética aprovecha el efecto magnetocalórico (MCE) para reemplazar los procesos de compresión y expansión de los sistemas convencionales por procesos de magnetización y desmagnetización de un material magnetocalórico [Hoyos, 2004].
A diferencia del ciclo de vapor, en los sistemas de refrigeración magnética el refrigerante (material magnetocalórico) es un sólido y no se puede bombear a través de intercambiadores de calor. Por tanto se emplea un fluido que transfiere la energía entre el refrigerante magnético y los depósitos [Zimm, et al., 1998]. Este sistema de refrigeración presenta grandes ventajas ambientales y energéticas. Al suprimir el compresor, aumenta la eficiencia y reduce la emisión de CO2. También disminuye el efecto invernadero causado por los CFC y HFC, porque reemplaza los refrigerantes del ciclo de vapor por un refrigerante magnético y un fluido, que puede ser agua o helio dependiendo de la temperatura de aplicación [Steyert, 1978].
La manifestación del efecto magnetocalórico como un cambio de entropía isotérmico o un cambio de temperatura adiabático, permite obtener diferentes ciclos termodinámicos. En este artículo se presentan los principios termodinámicos de los ciclos magnéticos de Carnot y de Brayton, señalando las limitaciones termodinámicas de los sistemas de refrigeración que emplean el ciclo de Carnot. Adicionalmente, se presenta la descripción del ciclo de Regeneración Magnética Activa (AMR).
El ciclo de Carnot se realiza en dos procesos de cambio de temperatura adiabático y dos procesos de cambio de entropía isotérmico. Esto permite estudiar directamente las manifestaciones del MCE. La aplicación del ciclo de Carnot se restringe a temperaturas inferiores a 20K, debido al aumento de la capacidad de calor con el aumento de la temperatura. Al aumentar la capacidad de calor disminuye el MCE y aumenta la energía necesaria para cambiar el orden magnético del material. El intervalo de temperaturas de operación está limitado por el cambio de temperatura adiabático a temperaturas inferiores a 22K [Hoyos, 2004].
En la refrigeración magnética el refrigerante es un sólido y no un fluido, por tanto no es apropiado emplear el término calor específico, tanto la entropía como la capacidad de calor son propiedades extensivas.
El ciclo de Brayton es un ciclo regenerativo que permite obtener amplios intervalos de temperatura de operación. Puede operar a temperaturas altas, porque el intercambio de calor entre el refrigerante magnético y el fluido no se realiza en los procesos de cambio de entropía isotérmico (como en el ciclo de Carnot), sino en procesos en los que la intensidad magnética permanece constante.
Las principales aplicaciones de la refrigeración magnética han sido en licuefacción de gases, aplicaciones aeroespaciales, aplicaciones médicas de imágenes de resonancia magnética y el enfriamiento de sensores infrarrojos para aplicaciones científicas y militares [Kral y Barclay, 1991]. Se espera que en los próximos años se pueda emplear en aplicaciones comerciales a temperatura ambiente, en sistemas de aire acondicionado y refrigeradores domésticos.
2. TERMODINÁMICA DEL EFECTO MAGNETOCALÓRICO
Los sistemas de refrigeración aprovechan el cambio en la entropía de un material debido a la variación de parámetros externos, como la presión o la magnetización, para producir frío. Estos fenómenos son conocidos como efecto elastocalórico (ECE) y efecto magnetocalórico (MCE), respectivamente.
Los sistemas convencionales transfieren calor debido al cambio en la presión ejercida sobre un material en un proceso donde la intensidad magnética permanece constante (un campo magnético nulo es un caso particular). Los sistemas de refrigeración magnética emplean un principio inverso. En estos sistemas, la transferencia de calor se produce cuando cambia el campo magnético aplicado sobre el material, en un proceso en el que la presión permanece constante [Hoyos, 2004].
Durante un proceso adiabático podrían cambiar simultáneamente la presión y el campo magnético externo, produciendo el efecto magneto-elastocalórico (MECE). Actualmente no existen estudios sobre éste fenómeno y en las aplicaciones de la refrigeración magnética lo común es evitar al máximo los cambios de presión para despreciar el ECE y utilizar sólo el MCE [Tishin, 2000].
Cuando se aplica un campo magnético externo a un material ferromagnético, a una temperatura cercana a su temperatura de transformación de fase magnética (temperatura de Curie), los momentos magnéticos de los electrones desapareados del nivel 3d (para hierro, níquel y cobalto) o del nivel 4f (para los lantánidos) se alinean paralelos a la dirección de la inducción del campo magnético aplicado. Esta alineación disminuye la entropía del material. Cuando se retira el campo magnético aplicado, los momentos magnéticos de los electrones se orientan libremente aumentando la entropía.
La magnetización y desmagnetización del material ferromagnético, a temperaturas cercanas a la temperatura de transformación magnética, favorecen el carácter reversible del proceso debido a los continuos cambios en el orden magnético. El MCE se manifiesta en dos formas. Cuando el cambio en el campo magnético se produce en un proceso adiabático aparece como un cambio de temperatura isoentrópico, de lo contrario (si no es adiabático) se manifiesta como un cambio de entropía isotérmico.
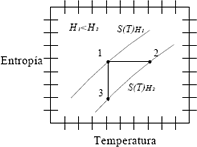
Existen dos tipos de MCE en los materiales ferromagnéticos, el MCE convencional y el MCE gigante (Figuras 1 y 2, respectivamente).
Figura 1. MCE en transformaciones de segundo orden. Curvas isomagnéticas de la entropía en función de la temperatura.
Figure 1. MCE in transformations of second order. Temperature dependence of the entropy in different magnetic fields.
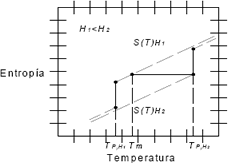
Figura 2. MCE en transformaciones de primer orden. Curvas isomagnéticas de la entropía en función de la temperatura.
Figure 2. MCE in transformations of first order. Temperature dependence of the entropy in different magnetic fields.
En el MCE convencional, la aplicación de un campo magnético externo en un proceso adiabático disminuye la entropía magnética. Como el proceso es adiabático aumenta la entropía de retícula, la cual está asociada a la distribución espacial de los átomos en la red cristalina (retícula), para mantener la entropía del sistema constante. El aumento de la entropía de retícula aumenta la temperatura del material (proceso 1-2 de la figura 1).
Cuando el material magnético intercambia calor con un medio externo, durante la aplicación o remoción del campo magnético externo, la temperatura permanece constante mientras la entropía cambia (proceso 1-3 de la figura 1).
La principal característica de las transformaciones de primer orden es la discontinuidad en la entropía (Figura 2). Para cada curva isomagnética de la entropía en función de la temperatura, existe una temperatura a la cual se produce un cambio abrupto en la entropía. La combinación de esta discontinuidad con el cambio en la magnitud de la intensidad del campo magnético produce un mayor cambio de entropía magnética que el observado en las de segundo orden.
El cambio de entropía magnética para las transformaciones magnéticas de primer orden, durante la magnetización y desmagnetización, se calculan, respectivamente, de las ecuaciones 1 y 2.
En ellas, se tiene la siguiente nomenclatura. Con una intensidad del campo magnético Hi la temperatura de transformación magnética de primer orden es TP,Hi, la entalpía de transformación es DEHi y la magnitud en la discontinuidad de la entropía es igual a la relación entre la entalpía y la temperatura de transformación. T1 es la temperatura de referencia para el nivel de entropía cero. Cl(T) y Ch(T) son respectivamente las capacidades de calor antes y después de la temperatura de transformación de primer orden [Pecharsky, et al., 2001].
A diferencia de las transformaciones de primer orden, en las de segundo orden la entalpía de transformación es nula y no existe diferencia en el comportamiento de la capacidad de calor, antes y después de la transformación, porque no se presentan transformaciones magnéticas que involucren cambios en la estructura cristalina, como ocurre en las transformaciones de primer orden.
La diferencia entre estas transformaciones magnéticas es similar a la diferencia entre el enfriamiento a temperatura constante por evaporación de liquido y el enfriamiento por la simple expansión del gas. La transformación magnética de primer orden y la evaporación del líquido utilizan la entalpía de transformación para incrementar su entropía en un proceso isotérmico, mientras que la transformación de segundo orden y la expansión del gas
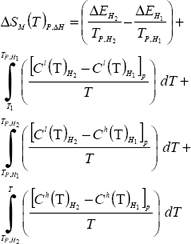
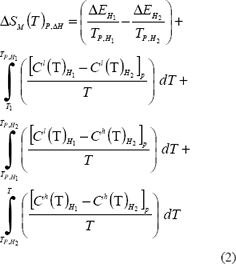
3. PRINCIPIOS TERMODINÁMICOS
Los sistemas de refrigeración magnética, aprovechan el cambio en la entropía de un material, debido al cambio isobárico en la intensidad magnética, para producir frío. La entropía del material depende de la temperatura y la intensidad magnética. Por tanto, el diferencial total de la entropía se puede calcular con la ecuación 3.
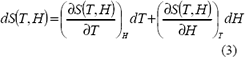
Esta ecuación se puede obtener a partir de la segunda ley de la termodinámica y deduciendo las ecuaciones de Maxwell asociadas a la entalpía y la energía libre de Gibbs.
Los procesos de magnetización y desmagnetización se consideran reversibles y el cambio en el volumen del material magnetocalórico despreciable. Esto se puede considerar cuando la histéresis del cambio del orden magnético es despreciable, como en el gadolinio. El cambio de energía interna, la entalpía y la energía libre de Gibbs se expresan, respectivamente, con las ecuaciones 4, 5 y 6 [Bejan, 1997]. Es importante resaltar que tanto la entalpía como la intensidad magnética tienen el mismo símbolo (H), para evitar la confusión en este artículo, la entalpía se representa como H*, mientras para la intensidad magnética se emplea el símbolo H.
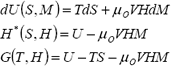
Ecuaciones (4), (5) y (6); respectivamente. Los diferenciales de la entalpía y la energía libre de Gibbs se calculan empleando el diferencial de la energía interna [Velásquez, et al., 2003].
![]()
La energía libre de Gibbs depende de la temperatura y la intensidad del campo magnético. Por lo tanto, su diferencial total se calcula con la ecuación 9.
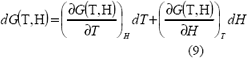
Al considerar la energía libre de Gibbs una función continua, sus derivadas parciales mixtas son iguales y se obtiene la ecuación de Maxwell que relaciona la entropía con la magnetización (ecuación 12).
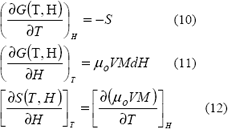
Al aplicar la segunda ley de la termodinámica para procesos reversibles y reemplazando la ecuación anterior, en el diferencial total de la entropía (ecuación 1), se obtiene:
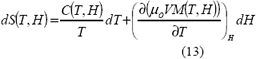
La ecuación 13 permite hallar el cambio de entropía isotérmico. Sin embargo, no permite calcular el cambio de temperatura adiabático de forma explícita. Este cálculo se obtiene teniendo en cuenta que la entropía total del material equivale a la suma de las entropías magnética, electrónica y de retícula (SM, SE, SL, respectivamente) [Tishin y Spichkin, 2002].
Un análisis riguroso señala que, a presión constante, estas entropías dependen de la temperatura y el campo magnético. Sin embargo, en el estudio del efecto magnetocalórico, se considera que la entropía magnética depende del campo magnético aplicado, mientras que las entropías electrónica y de retícula son independientes. Por tanto, al magnetizar o desmagnetizar el material la entropía magnética cambia mientras las entropías electrónica y de retícula permanecen constantes [Tishin y Spichkin, 2002].
Cuando el proceso no es adiabático el cambio en la entropía total es igual al cambio en la entropía magnética. Cuando el proceso es adiabático, la entropía total permanece constante (ecuación 14).
![]()
Por tanto, el cambio en la entropía magnética induce un cambio en las entropías de retícula y electrónica, de igual magnitud pero sentido opuesto. El cambio de entropía magnética se puede calcular con las ecuaciones 15 y16.
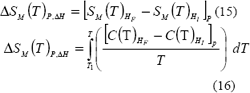
De la segunda ley de la termodinámica, considerando la capacidad de calor en función de la temperatura y el campo magnético como una función continua, y reemplazando la ecuación 16 en la 14, se obtienen las ecuaciones para el cambio de temperatura adiabático durante la desmagnetización y magnetización (ecuaciones 17 y 18, respectivamente) [Hoyos, 2004].
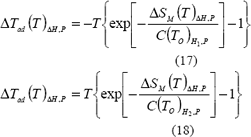
4. CICLOS MAGNÉTICOS
La manifestación del efecto magnetocalórico como un cambio de entropía isotérmico o un cambio de temperatura adiabático, permite adecuar los sistemas de refrigeración magnética para obtener diferentes ciclos termodinámicos.
En los estudios sobre la refrigeración magnética, es común encontrar representaciones de estos ciclos tanto en diagramas de la temperatura en función de la entropía como en diagramas de entropía en función de la temperatura. En este trabajo se emplean diagramas de la temperatura en función de la entropía para representar los ciclos de Carnot y de Brayton [Kral y Barclay, 1991].
Inicialmente, los refrigeradores magnéticos operaban con el ciclo de Carnot. Sin embargo, actualmente emplean ciclos regenerativos como los ciclos de Brayton y de regeneración magnética activa (AMR). Este cambio se presenta porque con el ciclo de Carnot, la aplicación de la refrigeración magnética está limitada por el cambio de temperatura adiabático del material magnetocalórico. El ciclo de Carnot se emplea en aplicaciones criogénicas, con intervalos de temperatura cercanos a 20K, mientras que los ciclos regenerativos pueden operar a temperaturas más altas, con intervalos de temperatura mayores [Kral y Barclay, 1991].
La transferencia de calor en el ciclo Brayton se presenta de forma diferente a la del ciclo de Carnot. En este último la transferencia de calor entre el fluido y el material magnetocalórico (también llamado refrigerante magnético) ocurre en un proceso isotérmico, mientras el material se magnetiza o desmagnetiza. En cambio, en el ciclo de Brayton la transferencia de calor se realiza en los procesos donde la intensidad magnética permanece constante. Esto permite una mayor transferencia de calor entre el material magnetocalórico y el fluido.
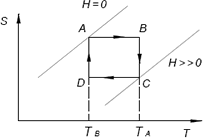
El ciclo de Carnot es el ciclo más simple y representativo del MCE [Barclay, et al., 1984]. Este ciclo se realiza en cuatro procesos, dos adiabáticos y dos isotérmicos (Figura 3).
Figura 3. Ciclo magnético de Carnot. Este ciclo se realiza en dos procesos adiabáticos y dos procesos isotérmicos.
Figure 3. Carnot cycle. This cycle comprises four steps: two adiabatic and two isothermal.
Inicialmente, el refrigerante magnético se magnetiza parcialmente (proceso AB), aumentando su temperatura adiabáticamente desde TBhasta TA. Luego aumenta la intensidad del campo magnético aplicado para completar la magnetización y se remueve el aislamiento térmico del refrigerante para permitir el intercambio de calor con el fluido (proceso BC). En este proceso, el refrigerante mantiene su temperatura constante mientras que el fluido absorbe el calor generado en el refrigerante debido a la magnetización. En el proceso CD disminuye el campo magnético aplicado, esto disminuye la temperatura del refrigerante adiabáticamente, desde TAhasta TB. Finalmente, el ciclo se completa cuando el material se desmagnetiza completamente durante el proceso DA.
En el proceso DA, el refrigerante intercambia calor con el fluido recobrando la energía perdida durante la desmagnetización. Para garantizar el buen funcionamiento del sistema, el fluido expulsa la energía absorbida del refrigerante magnetizado al sumidero y absorbe la energía cedida al refrigerante desmagnetizado del sistema a refrigerar.
Los cambios de temperatura adiabáticos de los procesos CD y BA, se pueden calcular, respectivamente, de las ecuaciones 17 y 18. El intercambio de calor con el fluido durante los procesos BC y DA (ecuaciones 19 y 20, respectivamente), se obtiene a partir del correspondiente cambio de entropía isotérmico calculado con la ecuación 10.
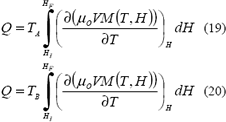
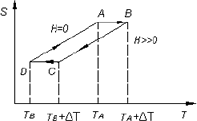
El ciclo de Brayton se realiza en cuatro procesos, dos adiabáticos y dos donde la intensidad del campo magnético aplicado permanece constante (Figura 4).
Figura 4. Ciclo Brayton. Este ciclo se realiza en dos procesos adiabáticos y dos procesos con intensidad magnética constante.
Figura 4. Brayton Cycle. This cycle comprises four steps: two adiabatic and two isofield.
En este ciclo la transferencia de calor se realiza en los procesos donde la intensidad magnética permanece constante. Por tanto, se obtienen intervalos de temperatura superiores a los del ciclo de Carnot [Barclay, 1983].
Inicialmente el refrigerante magnético se encuentra por fuera de la región de alto campo magnético, a una temperatura TAcuando entra a la región de alto campo magnético su temperatura incrementa adiabáticamente, desde TAhasta TA+DT, debido al efecto magnetocalórico. Cuando termina el proceso adiabático, el campo magnético aplicado permanece constante y el refrigerante emite energía al fluido, disminuyendo la temperatura desde TA+DT hasta Tb+DT. Luego, el refrigerante se separa del fluido y entra a la región de bajo campo magnético, y su temperatura disminuye desde Tb+DT hasta TBdebido al efecto magnetocalórico.
Finalmente, en la región de bajo campo magnético el refrigerante intercambia calor con el fluido, absorbiendo energía de éste para aumentar la entropía y la temperatura hasta TA. El ciclo realizado por el fluido, es similar al efectuado cuando el refrigerante ejecuta el ciclo de Carnot. El fluido expulsa al sumidero la energía absorbida del refrigerante magnetizado y absorbe del sistema a refrigerar la energía cedida al refrigerante desmagnetizado.
Los cambios de temperatura adiabáticos de los procesos CD y BA se calculan igual a los del ciclo de Carnot. Es decir, se obtienen, respectivamente, de las ecuaciones 17 y 18. El intercambio de calor con el fluido durante los procesos BC y DA, se obtiene, respectivamente, de las ecuaciones 21 y 22, a partir del correspondiente cambio de entropía (con el campo magnético aplicado constante) calculado con la ecuación 13.
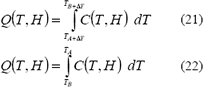
El intervalo de temperaturas de operación del ciclo de Carnot está limitado por el cambio de temperatura adiabático de los procesos CD y BA. Cuando la temperatura aumenta, aumenta la capacidad de calor. En las ecuaciones 17 y 18 es evidente la disminución del cambio de temperatura adiabático cuando aumenta la capacidad de calor. Cuando la entropía de retícula es muy grande comparada con la entropía magnética, el cambio de temperatura adiabático del material es insignificante.
La entropía de retícula aumenta con el aumento de la vibración de los átomos, la cual crece con el aumento de la temperatura. Esto limitó la aplicación de la refrigeración magnética a temperaturas inferiores a 20K [Saito, et al., 2003]. El ciclo de Carnot no se emplea a temperaturas altas, esto se debe a la constitución del ciclo. La operación mediante dos procesos continuos de magnetización (procesos AB y BC) y dos procesos continuos de desmagnetización (procesos CD y DA), requieren campos magnéticos muy grandes para disminuir la vibración de los átomos.
La aplicación de la refrigeración magnética a temperaturas más altas se realiza desde la década de 1970. En estas aplicaciones se aprovecha la transformación de fase magnética de un material ferromagnético, entre los estados ferromagnético y paramagnético. Por tanto, el rango de temperatura de aplicación está limitado a la vecindad de la temperatura de transformación. En el caso del gadolinio, el mejor material magnetocalórico a temperatura ambiente, el rango de temperatura máximo para el ciclo de Carnot es 22K [Saito, et al., 2003].
En aplicaciones de la refrigeración magnética a temperaturas altas, se emplean tres tipos de regeneradores: un regenerador externo, un regenerador interno y el regenerador magnético activo [Yu, et al., 2003].
El ciclo Brayton que se describe en el artículo, es un regenerador externo. En este tipo de regeneradores, la transferencia de calor entre el material regenerador (generalmente un sólido) y el material refrigerador se realiza a través de un fluido. En el regenerador interno, el material regenerador (generalmente un fluido) y el material refrigerante se colocan dentro del regenerador, por tanto la transferencia de calor se realiza directamente entre ellos.
En el AMR, el material magnético no sólo es el material refrigerante sino también el regenerador. Esto disminuye las perdidas irreversibles por los procesos de transferencia de calor adicionales en el regenerador externo y la mezcla de las regiones del fluido regenerador con diferentes temperaturas en el regenerador interno. De los tres regeneradores, el más ineficiente es el regenerador interno, sin embargo tiene gran valor histórico al ser el empleado en la primera aplicación de la refrigeración magnética a temperatura ambiente [Brown, 1976].
De acuerdo a la capacidad de calor relativa entre el fluido y el material refrigerante se tienen dos aplicaciones limites. En la primera, la capacidad de calor del fluido es mucho mayor que la del material refrigerante (regenerador interno). En la segunda, la capacidad de calor del fluido es mucho menor que la del material refrigerante (AMR). En el regenerador interno, el gradiente de temperatura es afectado fácilmente por la acción del fluido. En el AMR, el gradiente de temperaturas es estable y la rata de flujo requerida para una carga de refrigeración dada es mucho menor que en el regenerador interno.
El mecanismo de transferencia de calor del AMR es similar al de un regenerador ordinario, excepto porque el cambio de temperatura se debe a la aplicación y remoción del campo magnético, es decir, el término activo se refiere a la aplicación y remoción del campo magnético, en oposición a un regenerador normal o pasivo donde el campo magnético es nulo.
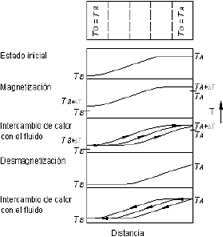
Este ciclo permite obtener intervalos de temperatura de operación muy superiores a los obtenidos por ciclos termodinámicos convencionales, en un volumen considerablemente menor. Se pueden obtener intervalos de temperatura desde 50K para un lecho magnético conformado por un solo material hasta intervalos superiores a 300K para un lecho magnético conformado por varios materiales magnetocalóricos ordenados de menor a mayor temperatura de Curie [Hoyos, 2004]. Los procesos termodinámicos, son similares a los realizados en el ciclo de Brayton (Figura 5). Primero, el lecho magnético es magnetizado, por lo tanto el material magnético aumenta la temperatura. Después de la magnetización, el fluido absorbe energía del lecho magnético en un proceso donde el campo magnético aplicado permanece constante. El fluido entra por el extremo de menor temperatura y sale por el de mayor temperatura.
Figura 5. Perfil de temperaturas del ciclo AMR. La capacidad de calor del fluido es menor a la del lecho magnético.
Figure 5. Temperatures profile of AMR cycle. Heat capacity of the fluid blow through the magnetic bed is leseer than that of the magnetic bed.
Durante la desmagnetización todos los elementos del lecho magnético alcanzan las temperaturas locales más bajas del ciclo, por lo tanto cuando el fluido entra nuevamente al lecho magnético en lugar de absorber energía, expulsa energía calentando el lecho magnético. En este proceso, el fluido entra por el extremo de mayor temperatura y sale por el extremo de menor temperatura.
Esta descripción sólo es correcta cuando el lecho magnético tiene una capacidad de calor muy superior a la del fluido, y cumple tanto la función de material refrigerante como la de regenerador [Barclay y Steyert, 1982].
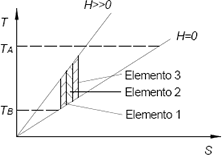
En un ciclo AMR ideal (sin generación de entropía) cada elemento del lecho magnético realiza un ciclo Brayton (Figura 6) en un intervalo de temperaturas que depende de su temperatura de Curie.
Figura 6. Ciclo AMR. El lecho magnético puede contener uno o más materiales, ordenados de menor a mayor temperatura de Curie.
Figure 6. Cycle AMR. Magnetic bed can composed of layers of different magnetic materials with Curie temperature increasing progressively.
Dentro del lecho magnético, los materiales magnetocalóricos, funcionan como un ensamble de refrigeradores elementales actuando en paralelo para intercambiar calor con el fluido que transfiere calor con los dos depósitos. Esto permite alcanzar un amplio intervalo de temperaturas [Kral y Barclay, 1991].
El problema principal es la generación de entropía. Para minimizarla, la temperatura dentro del lecho magnético debe aumentar gradualmente sin discontinuidades ni cambios abruptos, es decir, cuando el cambio en la entropía del lecho magnético se considera constante.
Esta condición limita considerablemente la utilización del ciclo del AMR y experimentalmente sólo se reportan dispositivos con un lecho magnético conformado por dos materiales magnetocalóricos [Hoyos, 2004]. Actualmente, las investigaciones están orientadas al diseño de refrigeradores magnéticos, estudiar la termodinámica de las transformaciones magnéticas de primer y segundo orden y realizar modelos del principio AMR.
La realización de modelos que describan apropiadamente la transferencia de calor entre el material refrigerante y el fluido, se constituye en la base para la aplicación comercial de la refrigeración magnética. Debido a la falta de estos modelos, no es posible calcular los parámetros de operación reales de un refrigerador con base en una carga de refrigeración dada, como la frecuencia de operación, el volumen del material refrigerante, el área de contacto, la magnitud del campo y la transferencia de calor en régimen transitorio.
5. CONCLUSIONES
La refrigeración magnética se constituye en una de las tecnologías más importantes y con mayor potencial debido a sus ventajas ambientales y energéticas frente a los sistemas convencionales. Sin embargo, involucra fenómenos termodinámicos muy complejos y poco estudiados como las transformaciones magnéticas de primer orden y el principio de regeneración magnética activa. El estudio de estos fenómenos y el desarrollo de modelos termodinámicos que validen los resultados experimentales son fundamentales para su aplicación comercial. La entalpía de las transformaciones de primer orden, aumenta la magnitud del efecto magnetocalórico. Sin embargo, la discontinuidad en la entropía puede disminuir considerablemente la reversibilidad del proceso.
Los ciclos de Carnot y de Brayton permiten estudiar los aspectos básicos de la refrigeración magnética. Sin embargo, la aplicación del ciclo de Carnot se limita a bajas temperaturas y la del ciclo de Brayton a bajos intervalos de temperatura. En aplicaciones comerciales se emplean los principios de la Regeneración Magnética Activa. En este ciclo, el material magnético realiza la función de refrigerante y regenerador, aumentando considerablemente la eficiencia y el intervalo de temperatura de operación.
NOMENCLATURA
C: Capacidad de calor
E: Entalpía de transformación
G: Energía libre de Gibbs
H: Intensidad magnética
H*: Entalpía
M: magnetización por unidad de volumen
Q: Calor
S: Entropía
T: Temperatura
U: Energía interna
V: Volumen
Caracteres griegos
mo = permeabilidad en el vacío
Subíndices
A: Alta Temperatura
ad: Adiabático
B: Baja temperatura
C: Relativo a la desmagnetización
E: Entropía de retícula
H: Intensidad constante
HI:: Relativo a la intensidad inicial
HF:: Relativo a la intensidad final
H1: Relativo al estado de baja intensidad
H2: Relativo al estado de alta intensidad
L: Electrónica
M: Magnética
O: promedio
p: Presión constante
T: Isotérmico
Superíndices
H: Posterior a la transformación de primer orden
l: Antes a la transformación de primer orden
REFERENCIAS [ Links ]
[2] BARCLAY, J., Wheel-Type Magnetic Refrigerator. USP No 4,408,463, Octubre, 1983. [ Links ]
[3] BARCLAY, J., OVERTON, W., Y STEWART, W., Magnetic Refrigeration Apparatus and Method. USP No 4,459,811, Julio, 1984. [ Links ]
[4] BARCLAY, J., STEYERT, W., Active Magnetic Regenerator. USP No 4,332,135, Junio, 1982. [ Links ]
[5] BROWN, GERALD, Magnetic Heat Pumping. USP No 4,069,028, Noviembre, 1976. [ Links ]
[6] HOYOS , J., Refrigeración magnética, Universidad Nacional de Colombia (Tesis Ingeniería Mecánica), Medellín, 2004. [ Links ]
[7] KRAL, S., Y BARCLAY, J., Magnetic refrigeration: a large cooling power cryogenic refrigeration technology. Applications of cryogenic technology, Vol 10, 27-41, Plenum press, New York, 1991. [ Links ]
[8] PECHARSKY, V., GSCHNEIDNER, K., PECHARSKY, A., y Tishin, A., Thermodynamics of the magnetocaloric effect. Physical review B, Vol 64, No 144406, 2001. [ Links ]
[9] SAITO, A., KOBAYASHI, T., SAWA, T., Y SAHASHI, M., Magnetic material. USP No 2003/0051774A1, Marzo, 2003. [ Links ]
[10] STEYERT, W. High temperature refrigerator. USP No 4,107,935. 1978. [ Links ]
[11] TISHIN, A. Adiabatic processes in magnetic materials. Advances in cryogenic engineering (materials), Vol 46, 2000. [ Links ]
[12] TISHIN, A., AND SPICHKIN, YOURI. Relationships of adiabatic, isothermal and field constant changes of a magnetic entropy. En: Advances incryogenic engineering: proceedings of the international cryogenic materials conference, Vol 48, CP614, p. 27-33, 2002. [ Links ]
[13] VELÁSQUEZ, JUAN ESTEBAN. CHEJNE, FARID. Hill, Alan. Producción de frío a partir de campos magnéticos. Parte II: Análisis termodinámico. En: Revista Facultad de Ingeniería, no 30, p. 71-77, 2003. [ Links ]
[14] YU, B., GAO, Q., ZHANG, B., MENG X., CHEN, Z., Review on research of room temperature magnetic refrigeration. International of Refrigeration, no 26, p. 622-636, 2003. [ Links ]
[15] ZIMM, C., JASTRAB, A., STERNBERG, A., PECHARSKY, V., GSCHNEIDNER, K., OSBORNE, M., Y ANDERSON, I., Description and Performance of a near-room temperature magnetic refrigerator. En: Advances in cryogenic engineering. Vol 43, p. 1759-1766, 1998. [ Links ]