PROGRAMA COMPUTACIONAL DE SIMULACIÓN HIDRÁULICA DEL RIEGO POR SURCOS USANDO EL MODELO DE ONDA CINEMÁTICA (PARTE I: Fundamento teórico)

HYDRAULIC SIMULATION SOFTWARE OF THE IRRIGATION BY FURROWS USING THE KINEMATICS WAVE MODEL (PART I: Theoretical foundation)

ALEJANDRO BECERRA
Ingeniero Agrícola,Universidad Nacional de Colombia Sede Palmira, abecerr@unalmed.edu.co y alejobero@yahoo.es

HAROLD TAFUR HERMANN
Ingeniero Agrícola – Doctor en Ciencias. Universidad Nacional de Colombia Sede Palmira, tafurh@palmira.unal.edu.co

Recibido para revisar 15 de Julio de 2004, aceptado 29 de Agosto de 2005, versión final 5 de Mayo de 2006

RESUMEN: Pretendiendo simular en forma rápida y precisa los eventos de riego por surcos, nace la idea de desarrollar un programa computacional, ya que cuando se utilizan los modelos de simulación hidráulica, el volumen de cálculos involucrados puede resultar considerable; por tanto para hacer versátil y funcional el empleo de estos modelos, es conveniente trabajarlos en forma automatizada. En este artículo se expone el fundamento teórico del modelo de simulación hidráulica onda cinemática, el cual fue usado para el desarrollo de un programa computacional que simula los diferentes eventos en el riego por surcos. Para el efecto se construyó un algoritmo bien estructurado para cada fase del riego (avance, llenado y recesión) y para cada frente de aplicación (diseño y evaluación). El modelo de onda cinemática utiliza las constantes de la ecuación de infiltración Kostiakov Lewis y tiene la posibilidad de simular el movimiento del agua en el perfil longitudinal del suelo y cálculo del área de humedecimiento en la sección transversal del surco.

PALABRAS CLAVE: Riego por surcos, onda cinemática, simulación hidráulica, programa computacional, eficiencias de riego.

ABSTRACT: Trying to simulate in fast and precise way the events irrigation by furrows, is born the idea to develop a software, since when the models of hydraulic simulation are used, the volume of involved calculations can be considerable; therefore to make versatile and functional the employment of these models, is convenient to work them in automated way. In this paper the theoretical foundation of the model of hydraulic simulation wave kinematics is exposed, which were used for the development of software that simulates the different events in the irrigation by furrows. For the effect a structured affluent algorithm for each phase of the irrigation (advance, ponding and recession) and for each front of application was constructed (design and evaluation). The wave model kinematics uses the constants of the equation of Kostiakov infiltration Lewis and has the possibility of simulating the movement of the water in the longitudinal profile of soil and calculation of the flow area in the cross-sectional of the furrow.

KEY WORDS: Furrow Irrigation, Kinematics wave, Simulation hydraulic, Software, Irrigation efficiencies.

1. INTRODUCCION

Existen diferentes variables que influencias el desarrollo del sistema de riego por surcos, tales como: velocidad, tipo de flujo, tamaño, pendientes del surco, forma, rugosidad y características de infiltración. Otras variables son definidas por el proyectista como: tiempo de riego, longitud de surco, espaciamiento entre surcos, lámina aplicada. Para lograr un buen diseño de riego se deben considerar estas variables y sus interacciones entre las mismas (REDDY y CLYMA, 1981).

Con la finalidad de optimizar los parámetros antes mencionados y economizar tiempo y dinero, en pruebas de campo, ELLIOTT et al. (1983) sugieren el uso de la simulación del comportamiento hidráulico de las fases del riego. Para tal efecto el modelamiento matemático del riego por superficie en procesos hidráulicos de escurrimiento en medios porosos ha sido simulado por modelos con un amplio grado de complejidad y precisión (RAYEJ y WALLENDER, 1987; STRELKOFF y SOUZA, 1984; WALKER y HUMPHERYS, 1983; WALLENDER y RAYEJ, 1985). Estos modelos simulan el avance del agua a lo largo de la superficie del suelo, como un volumen de agua infiltrado o volumen escurrido o percolado. Los modelos mas comunes en orden de complejidad, del mas simple al mas complejo son: balance volumétrico, onda cinemática, cero inercia e hidrodinámico. Los modelos: hidrodinámico, cero inercia y onda cinemática son basados en la solución numérica de ecuaciones diferenciales de conservación de masa y energía, y por ser más completos, predicen mejor el proceso de riego por superficie (RAGHUWANSHI y WALLENDER, 1994).

Las anteriores consideraciones sugieren la necesidad de estudiar con más detalle el manejo de los modelos de simulación ya mencionados. De este modo, este trabajo tiene como objetivo general, desarrollar un programa computacional (software) de simulación hidráulica del riego por surcos usando el modelo de Onda Cinemática.

Para el diseño de los sistemas de riego superficiales, se recomiendan los modelos de simulación, porque son un medio económico para analizar múltiples condiciones de funcionamiento y escenarios de operación, por ello el interés de abordar este modelo, el cual es el más sencillo de los modelos simplificados, pero de acuerdo a WALKER y SKOGERBOE (1987), tiene la capacidad para representar los eventos de riego por superficie con buena precisión.

2. MATERIALES Y MÉTODOS

2.1 Modelos de simulación hidráulica para riego por superficie

Dependiendo del grado de las simplificaciones hechas a las ecuaciones iniciales básicas, hay esencialmente, cuatro grandes grupos de modelos disponibles que permiten simular el escurrimiento del agua sobre la superficie del suelo, que han sido utilizados por varios investigadores. En orden decreciente de complejidad, son los siguientes: Hidrodinámico, Cero inercia, Onda cinemática y Balance volumétrico (ELLIOTT y WALKER, 1982; STRELKOFF y SOUZA, 1984; RAYEJ y WALLENDER, 1985; RAYEJ y EALLENDER, 1987; RAYEJ y WALLENDER, 1988; SMERDENSON et al., 1988; WALLENDER y RAYEJ, 1980; WALLENDER y YOKOKURA, 1991; SOARES, 1998).

2.1.1 Modelo Hidrodinámico

El hidrodinámico es el más completo de los modelos existentes, ya que no se hacen simplificaciones y a se basa en la solución de las ecuaciones 1 y 2 conocidas en el flujo de agua en canales abiertos como ecuaciones de Saint-Venant (CHOW, 1959, WALKER y SKOGERBOE, 1987).

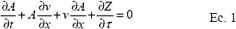
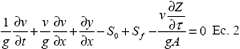
donde:

A = área de sección transversal de escurrimiento, L²;
T = tiempo acumulado, T;
V = velocidad media de flujo, L/T;
x = distancia desde la entrada del surco, L;
Z = volumen infiltrado acumulado por unidad de longitud, L³/L;
t = tiempo de oportunidad de infiltración, T;
g = aceleración de gravedad, L/T²;
y = profundidad de flujo, L;
S₀ = Pendiente media longitudinal de flujo, L/L;
S_f = pendiente de la línea de energía. L/L;
c' = constante numérica resultante de la derivación, en el uso del principio de la conservación de cantidad de movimiento o de energía, adimensional.

Las ecuaciones 1 y 2 corresponden respectivamente a las ecuaciones de conservación de la masa o continuidad y a la de conservación de la energía o momentum; son de tipo diferencial parcial de primer orden, una dimensión, no lineal e hiperbólicas. WALKER y SKOGERBOE (1987) desarrollaron dos procedimientos para solucionar numéricamente estas ecuaciones utilizando el método de las características (BASSETT, 1972; KINCAID et. al., 1972; BASSETT y FITZSIMMONS, 1976; KATAPODES y STRELKOFF, 1977) y el método de integración eulereana (SOUZA, 1981). El método de las características, primero convierte las ecuaciones diferenciales parciales en ecuaciones diferenciales ordinarias, y como ambas ecuaciones deben ser resueltas simultáneamente para cada coordenada de tiempo y espacio, se asume que una solución simultánea puede ser obtenida por la combinación lineal de ambas ecuaciones. La integración eulereana, presentada por STRELKOFF Y KATAPODES (1977) es una aproximación numérica a las dos ecuaciones, basada en el concepto de volumen de control deformable, comprendido por celdas deformables individuales. Cuando la principal deformación ocurre en el inicio del sistema, las celdas avanzan a una cierta velocidad, y un análisis conocido como sistema LaGrangeano es utilizado para simular la fase de avance; si la principal deformación ocurre en el contorno del final, como en las fases de reposición y recesión, las celdas son estacionarias y el sistema es conocido como Eulereano.

Esta solución numérica presentada por STRELKOFF y KATAPODES (1977) consta de la integración de las ecuaciones de Saint-Venant sobre un plano x-t, expresando valores conocidos sobre la línea de tiempo ti-1, y valores desconocidos sobre una línea de tiempo corriente, ti. Esto conduce a un sistema de ecuaciones que pueden ser resueltas por alguna técnica de solución de matrices. Entre tanto, de la simulación de una o más de las fases de riego por superficie, utilizando las ecuaciones de Saint-Venant, resulta una matriz de los coeficientes de tipo esparcido y en la forma de faja con cinco diagonales que normalmente se han resuelto con la ayuda de un algoritmo denominado Preissmann double-sweep, de uso específico para este tipo de matriz. Este procedimiento matemático fue desarrollado por J.A. Liggett y J. A. Cunge, en 1975, y presentado con detalles por WALKER y SKOGERBOE (1987).

2.1.2 Modelo Cero inercia

A partir del modelo hidrodinámico STRELKOFF Y KATAPODES (1977) partieron de unas determinaciones para su simplificación, en la que en vista de los valores bajos de velocidad decidieron ignorar los términos de inercia, llegando así al modelo de Cero Inercia, descrito en las siguientes ecuaciones:

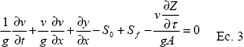
Las simplificaciones que llegan al modelo de Cero inercia fueron hechas inicialmente por STRELKOFF Y KATAPODES (1977) y posteriormente por CLEMMENS (1978), en las que consideraron que para valores del número de Froude menores a 0.2, los términos eliminados de la ecuación de la energía no comprometían la precisión. Estas suposiciones fueron luego comprobadas por los autores de forma experimental y comparando simulaciones hechas con el modelo hidrodinámico.

2.1.3 Modelo Onda Cinemática.

El modelo denominado de Onda cinemática conserva la ecuación de continuidad, pero simplifica al máximo la de energía, llegando a la siguiente expresión:

Es necesario combinar las ecuaciones de continuidad y la de energía (Ec. 5) para lograr representar adecuadamente los procesos que se desarrollan en el riego por superficie. En el modelo de onda cinemática se parte del supuesto que el flujo es permanente y uniforme.

2.1.4 Modelo de Balance Volumétrico.

Otro de los modelos de simulación de riego por superficie es el de Balance Volumétrico y corresponde al modelo más simple; ha sido descrito y utilizado por diferentes investigadores en la simulación del avance del riego por superficie y para resolver el problema inverso del riego por superficie (WALLENDER y RAYEJ, 1987; WALKER Y SKOGERBOE, 1987, y TAFUR et. al., 2000). El modelo expresa el balance de masa entre los volúmenes de agua aplicado, almacenado en la superficie de flujo y el infiltrado durante la fase de avance. De esta forma el modelo establece que el volumen de agua aplicado es igual al volumen de agua en la superficie más el volumen de agua infiltrada. La expresión general del modelo aplicada a surcos o melgas sería:

donde:

V_ap: Volumen aplicado
V_s: Volumen superficial
V_i: Volumen infiltrado.

2.2 Desarrollo teórico del modelo de onda cinemática

2.2.1 Fase de Avance

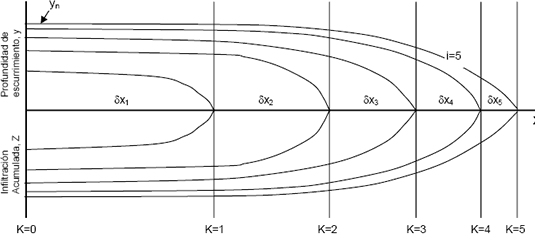
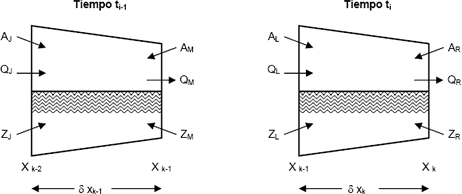
Durante la fase de avance del agua en el surco, el modelo considera el agua almacenada en superficie del suelo como un volumen de “control deformable”, limitado en un lado por la entrada del agua y ene. Otro por el frente de avance del agua; en la parte superior lo limita el perfil del agua superficial (el espejo del agua) y en la base por el frente mojado (figura 1 y 2). De esta forma, el volumen de agua fluye en el surco puede ser visto como una serie de volúmenes de control deformables, que consisten en subdivisiones o “células” de fluido en movimiento. La deformación de una célula ocurrida entre los tiempo t_i-1 y t_i, es ilustrada conforme a la figura 2. En la figura 2, los contornos o fronteras de izquierda y derecha del volumen de control deformable, en cada instante, son indicados por los términos X_k-2, X_k-1 y X_k. La definición también implica que para el tiempo ti, las fronteras de la izquierda y de la derecha se mueven una distancia dx_k-1 y dx_k respectivamente. El área mojada del flujo sobre el surco A, el volumen infiltrado por unidad de longitud, Z, y el caudal, Q, en los instantes ti-1 y ti, son acompañados de los subscritos J, M L y R, indicando el tiempo y la frontera que está siendo referenciada en la celta (WALKER y SKOGERBOE, 1987, SHAFIQUE, 1984, BECERRA y TAFUR, 2003).

Figura 1. Esquema de proceso de escurrimiento superficial e infiltración en intervalos de tiempo constante.
Figure 1. Process of superficial draining Scheme and infiltration in constant time intervals. Fuente: WALKER y SKOGERBOE (1987)

Figura 2. Esquema para definir una única celda para intervalos de tiempo sucesivos.
Figure 2. Scheme to define an only cell for successive time intervals. Fuente: ELLIOTT et al., (1982)

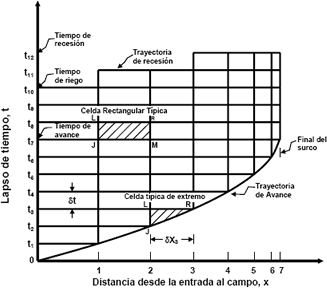
En la solución de las ecuaciones del modelo de onda cinemática (ecuaciones 1 y 5) se puede seguir el procedimiento presentado por WALKER y HUMPHEYS (1983) y WALLENDER (1993), considerando celdas rectangulares en el sistema conocido como coordenadas eulereanas (figura 3). Para el caso de la fase de avance en el análisis se pueden determinar tres tipos de celdas típicas para cada intervalo o incremento de tiempo a considerar, como son: primera celda, celta intermedia y celda punta. La celda punta siempre es triangular durante el avance y las otras dos son rectangulares (figura 3 y 4).

Figura 3. Solución eulereana, malla t-x para el modelo de onda cinemática.
Figure 3. Eulereana solution, mesh t-x for the wave model kinematics. Fuente: WALKER y SKOGERBOE (1987)

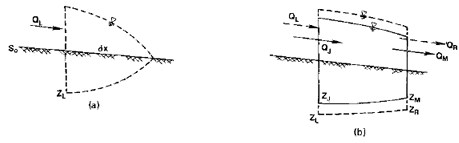
Figura 4. (a) Celda punta (b) Celda primera e intermedia (rectangular).
Figure 4. (a) Cell end (b) intermediate Cell first e (rectangular). Fuente: WALKER y SKOGERBOE (1987)

La celda punta es la que parta o define el avance en cada intervalo incremento de tiempo. En la solución numérica de las ecuaciones del modelo (ecuaciones del modelo (ecuaciones 1 y 5) se puede proceder de la siguiente manera: Integrando de la ecuación de continuidad o de conservación de masa se tiene:

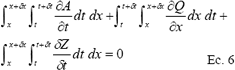
Desarrollando la primera integración se llega a:

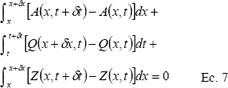
Y luego a:

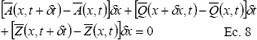
De la ecuación anterior, utilizando la notación notal J, L, M y R. Y con base en las figura 2 y 3 se puede llegar a:

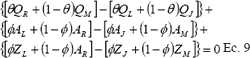
Donde q y f son factores de ponderación temporal y espacial, respectivamente, utilizados como compensación dentro del procesos de integración por la no linealidad de la ecuación de continuidad. Los valores de q y f varían entre 0 y 1 (WALKER y SKOGERBOE, 1987; RAGHUWANSHI y WALLENDER, 1994; SHAFIQUE, 1984), siendo valores muy aceptados 0.65 y 0.57 para q y f respectivamente (VIEIRA et al., 1997) ya que, valores por debajo de 0.5 producen inestabilidad en las soluciones (SHAYYA, et al., 1993).

ELLIOT et al, (1982) propusieron con una aproximación empírica para la sección hidráulica del tipo:

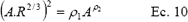
donde: r1 y r2 son parámetros de ajuste.

Si la relación de la ecuación 10 es considerada dentro de la ecuación de Manning se llega a:

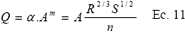
Donde:

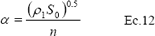
y

Sustituyendo Q de la ecuación de Manning (ecuación 11) en la ecuación 9 se puede tener la siguiente presentación:

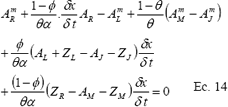
La ecuación 14 es una ecuación no lineal para A_R. En cualquier celda rectangular, los valores Q_J, Q_L, A_J y A_L (contorno izquierdo), están relacionados por la ecuación 11. Por tanto para la solución de la ecuación anterior se pueden reagrupar en dos constantes C1 y C₂ para cada intervalo de tiempo, teniendo como variable desconocida A_R. De esta forma se tiene:

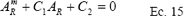
donde:

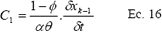
y

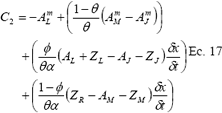
La ecuación 15 se resuelve explícitamente para cada intervalo de i, 1<i<N - 1, usando el método o técnica de Newton-Raphson.

El método de Newton Raphson es un proceso iterativo, en la que se busca encontrar la solución a una ecuación implícita, para este caso la ecuación 24 y se basa en la función:

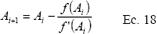
donde:

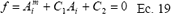
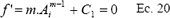
En cada valor calculado de A_R (A_i+1), en la siguiente interacción A_i toma el valor de A_i+1, hasta llegar a que A_i+1 sea aproximadamente igual a A_i. Generalmente se evalúa un error permisible entre el valor de A_i y A_i+1 para cada repetición y así no inducir a un ciclo infinito.

La ecuación 14 permite solucionar todas las celdas. Para el caso de la celda punta, donde A_R, A_J, A_M, Z_R, Z_J y Z_M son cero, durante el avance, la formulación matemática de la ecuación 14 queda reducida a:

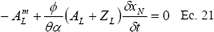
Como A_L es conocida de la solución de la celda anterior y Z_L en función del tiempo de oportunidad, la incógnita sería el avance que es:

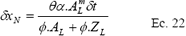
Las condiciones de frontera son A = Q = 0 y A = A₀, Q₀ = aA^m₀ para 0 <t<t₀ (donde t₀ es el tiempo de oportunidad de contacto).

2.2.2 Simulación de las Fases de: almacenamiento, agotamiento y recesión.

Cuando el flujo se corta en la entrada del surco, se asume que el área del borde izquierdo o entrada del surco, A_L, es cero inmediatamente. A partir de este corte del agua, inicia la fase de recesión; los cálculos son afectados de forma similar a la fase de avance y se asume que la recesión termina cuando el área mojada es menor que el 5% del valor del área a la entrada del surco.

2.2.3 Simulación del Proceso de infiltración.

Este proceso es el inverso de la simulación del avance, haciendo uso de las mismas relaciones matemáticas en forma modificada, ya que, la celda punta es analizada primero, luego las celdas intermedias y por último en la primera celda es donde se halla el valor de la infiltración para cada delta de tiempo evaluado. El procedimiento y las relaciones modificadas para cada tipo de celda son las siguientes:

Para la celda única punta:

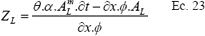
Con la ecuación 23 se calcula el valor de infiltración en el primer tiempo acumulado.

Para la celda punta, se resuelve la ecuación implícita por medio del método de Newton Raphson, explicado anteriormente, donde en este caso:

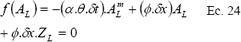
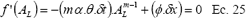
Para la celda intermedia, partiendo de la información anterior, se tiene:

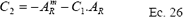
Nuevamente se hace uso del método de Newton Raphson para la solución de una ecuación y para esta solución se tiene que:

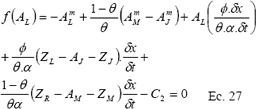
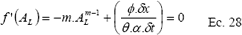
En la primera celda es donde se calcula el valor de la infiltración para el tiempo acumulado (en este avance evaluado) por medio de la siguiente ecuación (despejada Z_L de la ecuación 17) :

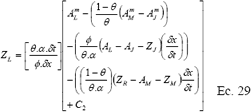
2.2.4 Corrección de la infiltración por perímetro mojado.

Normalmente en riego por superficie, la infiltración está dada para un caudal específico. Si el riego se afecta utilizando otro caudal, las condiciones de infiltración también cambian, considerando que la sección hidráulica es alterada (STRELKOFF Y SOUZA, 1984); por tanto, se debe corregir el valor de infiltración acumulada debido a la variación del perímetro mojado, al usar un caudal diferente al de la prueba. Para esto se pueden usar las siguientes expresiones (RAGHUWANSHI y WALLENDER, 1994):

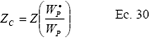
Y

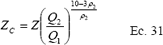
donde:

Z_C = Infiltración corregida por el perímetro mojado o caudal;
W^•_P = Perímetro mojado con un caudal de riego;
W_P = Perímetro mojado con un caudal de la ecuación de infiltración;
Q₂ = Caudal de riego;
Q₁ = caudal de infiltración;

Es decir, los respectivos perímetros mojados son calculados con base en un caudal y los parámetros derivados de la geometría del surco.

3. RESULTADOS

Con el modelo de Onda cinemática se desarrolló un programa computacional en el leguaje de programación Microsoft Visual Basic versión 6.0, capaz de simular los parámetros de la ecuación de Kostiakov - Lewis en las diferentes fases del riego por superficie.

REFERENCIAS

[1] BASSETT, D L. Mathematical model of water advance in border irrigatrion. In: Transaction of the ASAE, 1972 28 (5): 992 – 995.         [ Links ]
[2] BASSETT, D. L. y FITZSIMMONS, D. W. Simulatinng overland flow in border irrigation. In: Transaction of the ASAE, 1976 19 (4): 667 – 671.         [ Links ]
[3] CLEMMENS, A. J. Discussión of dimensionless solutions of border irrigation advance by KATAPODES N.D. e STRELKOFF (1977). In: Journal of Irrigation and Drainage Dic., ASCE, 1978 104 (IR3): 337-339.         [ Links ]
[4] CHOW, V. T. Open channel hydraulics. Tokyo: Mc Graw Hill International Book Company. 1959, 680p.         [ Links ]
[5] ELLIOTT, R. L. y WALKER, W. R. Field evaluation of furrow infiltration advance functions. In: Transaction of the ASAE, 1982 25 (2): 396-400.         [ Links ]
[6] ELLIOTT, R. L.; WALKER, W. R. y SKOGERBOE, G. V. Furrow irrigation advance rates; a dimensionless approach. In: Transaction of the ASAE, 1983 26 (82): 1722-1726.         [ Links ]
[7] KATAPODES, N. D. Y STRELKOFF, T. Hydrodinamics of border irrigation complete model. In: Journal of irrigation and Drainage Engineering, ASCE, 1977 103 (IR3): 309 – 324.         [ Links ]
[8] KINCAID, D. C., HEERMANN, D. F. y KRUSE, E. G. Hydrodinamics of border irrigation. In: Transaction of the ASAE, 1972 15 (14): 674 – 680.         [ Links ]
[9] RAGHUWANSHI, N. S. y WALLENDER, W. W. Stochastics seasonal furrow irrigation model. In: ASAE (An ASAE meeting presentation). Paper 942021, 1994. 20p.         [ Links ]
[10] RAYEJ, M. y WALLENDER, W. W. Furrow irrigation simulation time reduction. In: Journal of irrigation and Drainage Engineering, ASCE, 1985 101 (2): 134-146.         [ Links ]
[11] RAYEJ, M. y WALLENDER, W. W. Furrow model with specific intervals. In: Journal of irrigation and Drainage Engineering, ASCE, 1987 113 (4): 536-548.         [ Links ]
[12] RAYEJ, M. y WALLENDER, W. W. Time solution of kinematic-wave model with stochastic infiltraçâo. In: Journal of irrigation and Drainage Engineering, ASCE, 1988 114 (4): 605-621.         [ Links ]
[13] REDDY, J. M. y CLYMA, W. Optimal design of furrow irrigation systems. In: Transaction of the ASAE, 1981 24 (3): 617 – 623. 1981.         [ Links ]
[14] SHAFIQUE, Muhammad Sidolique. Zero-inertia model for basin-furrow irrigation. Colorado State University. Fort Collins. Dissertation. Degree of Doctor of Philosophy, 1984. 267p.         [ Links ]
[15] SHAYYA, W.H.; BRALTS, V.F. y SEGERLIND, L.J. Kinematic-wave furrow irrigation analysis: A finite element approach. In: ASAE. November-Dicember, 1993 36(6).         [ Links ]
[16] SMERDON, E. T., BLAIR, A. W. y REDDELL, D. L. Infiltration from irrigation advance data. I: theory. In: Journal of irrigation and Drainage Engineering. ASCE, 1988 114 (1): 4 - 7.         [ Links ]
[17] SOARES, A. A. Irrigaçâo por superficie. Brasilia, D. F., Curso de Engenharia da irrigation submódulo, 7.2. ABEAS, 1998. 62p.         [ Links ]
[18] SOUZA, F. Nonlinear hydrodinamic model of furrow irrigation. (pH.D Dissertation). Davis, University of California. 1981.STRELKOFF Y KATAPODES, 1977         [ Links ]
[19] STRELKOFF, T. Y KATAPODES, N. D. Border irrigation hydraulics with zero inertia. In: Journal of irrigation and Drainaje engineering, ASCE, 1977 103 (3): 325-342.         [ Links ]
[20] STRELKOFF, T. y SOUZA, F. Modeling effects of depth on furrow irrigation. In: Journal of irrigation and Drainage Engineering. ASCE, 1984 110 (4): 375 - 387.         [ Links ]
[21] TAFUR, H; ROJAS, H. y GONZÁLEZ ,C. El modelo del balance de volumen en la simulación del riego por superficie. Universidad Nacional de Colombia, Sede Palmira, 2000.         [ Links ]
[22] VIEIRA DE ACEVEDO, Carlos A.; WALKER W. R. y MERKLEY, G. P. Modelo de ondas cinemáticas en la solución del problema inverso del riego por surco en tiempo real. En: R. Bra. Eng. Agric Ambiental. Compina Grande, 1997 (1): 35 – 41.         [ Links ]
[23] WALKER, W. R. y HUMPHERYS, A. S. Surface irrigation Hydraulics. Davis, University of California, 1983. 44p.         [ Links ]
[24] WALKER, W. R. y SKOGERBOE, G. V. Surface irrigation: theory and practice. New Jersey: Prentice Hall, Inc., Englewood Cliffs, 1987, 386p.         [ Links ]
[25] WALLENDER, W. W. Surface irrigation Hydraulics. Davis, University of California. 1993, 44p.         [ Links ]
[26] WALLENDER, W. W. y RAYEJ, M. Zero-inertia surge model with met-dry advance. In: Transaction of the ASAE, 1985. 28 (5): 1530 – 1534.         [ Links ]
[27] WALLENDER, W. W. y RAYEJ, M. Economic optimization of furrow irrigation with uniform and non-uniform soil. In: Transaction of the ASAE, 1987 30 (5): 1425-1429.         [ Links ]
[28] WALLENDER, W. W. y RAYEJ, M. Shooting method for Saint-Vernant equations of furrow irrigation. In: Journal of irrigation and Drainage Engineering. ASCE, 1990 116 (1): 114-112.         [ Links ]
[29] WALLENDER, W. W. y YOKOKURA, J. Space solution of kinematic-wave model by time iteration. In: Journal of irrigation and Drenaige Engeneering, ASCE, 1991 117 (1): 140-144.         [ Links ]