TENDENCIAS EN LA PREDICCIÓN Y ESTIMACIÓN DE LOS INTERVALOS DE CONFIANZA USANDO MODELOS DE REDES NEURONALES APLICADOS A SERIES TEMPORALES

TENDENCIES IN THE PREDICTION AND ESTIMATION OF THE CONFIDENCE INTERVALS USING MODELS OF NEURONAL NETWORKS APPLIED TO TEMPORARY SERIES

JUAN DAVID VELÁSQUEZ H.
Escuela de Sistemas, Facultad de Minas, Universidad Nacional de Colombia, jdvelasq@unalmed.edu.co

ISAAC DYNER R.
Escuela de Sistemas, Facultad de Minas, Universidad Nacional de Colombia, idyner@unalmed.edu.co

REINALDO C. SOUZA.
Facultade de Engenharía Elétrica, Pontificia Universidade Catolica – Rio do Janeiro, reinaldo@ele.puc-rio.br

Recibido para revisión 16 de Abril de 2004, aceptado 28 de Marzo de 2005, versión final 28 de Abril de 2006

RESUMEN: En este artículo, se discute el estado del arte en la estimación de la predicción varios pasos adelante para modelos de series temporales no lineales basados en perceptrones multicapa. Se revisan las principales tendencias para la estimación de pronósticos puntuales e intervalos de confianza. En adición, se argumenta sobre los principales problemas abiertos para investigación futura en la predicción de series temporales usando redes neuronales.

PALABRAS CLAVE: Predicción, intervalos de confianza, redes neuronales artificiales.

ABSTRACT: .In this paper, we discuss the state-of-art in estimating multiple steps ahead forecast for nonlinear time series models based on multilayer perceptrons. We review the main trends for estimating the point forecasts and confidence intervals. In addition, we argue the principal open issues for future research in time series forecasting using neural networks.

KEYWORDS: Prediction, confidence intervals, artificial neural networks.

1 INTRODUCCIÓN

Los modelos de redes neuronales artificiales, así como otros modelos no lineales, han sido principalmente usados en la predicción de series temporales no lineales (Clements et al, 2004). No obstante, la problemática asociada con la predicción y la estimación de sus intervalos de confianza asociados, ha sido estudiada primordialmente desde la perspectiva de la Estadística y la Econometría, dándosele poca relevancia desde el punto de vista de la Inteligencia Artificial.

En este artículo, se introduce a todos aquellos profesionales e investigadores no familiarizados con este problema, en las tendencias actuales y las principales direcciones de investigación sobre la construcción de pronósticos y la estimación de intervalos de confianza.

2 EL MODELO

Un perceptron multicapa (MLP, Multilayer Perceptron) es un modelo estadístico no paramétrico de regresión no lineal (Sarle, 1994), que desde un punto de vista biológico imita la estructura masivamente paralela de las neuronas en el cerebro (Masters, 1993); su capacidad de tolerancia ante información incompleta, inexacta o contaminada con ruido (Masters, 1993), los ha hecho populares en la modelación empírica de series temporales no lineales; Zhang, Patuwo y Hu (1998) presenta una revisión general sobre el estado del arte, mientras que aplicaciones específicas son presentadas por Heravi, Osborn y Birchenhall (2004), Swanson y White (1997a; 1997b), Faraway y Chatfield (1998), Darbellay y Slama (2000) y Kuan y Liu (1995) entre muchos otros.

La Figura 1 representa de forma pictórica, la arquitectura del MLP definido por la ecuación:

Figura 1. Perceptron Multicapa
Figure 1. Multilayer Perceptron.

el cual se encuentra conformado por una capa de entrada, una capa oculta y una cada de salida; el vector de parámetros, W = [b*, b_h, a*,_h, a_p,h], h=1…H, p = 1…P, representa los pesos asociados a las conexiones entre las diferentes neuronas; H representa el número de neuronas en la capa oculta; P es el número de rezagos de la variable dependiente; y g() es la función de activación de las neuronas de la capa oculta. It representa la información disponible en el instante t, I_t = {y_t-1, y_t-2,…}. y_t* es una variable aleatoria cuya distribución de probabilidades es caracterizada por su valor esperado:

y su varianza:

3 ESTIMACIÓN DE LOS PARÁMETROS DEL MODELO

El problema de identificación de los parámetros de (1), consiste en determinar los valores del vector W, tal que se minimice alguna medida del error entre los valores reales y_t y los calculados E[y_t*]. Si se asume que los errores, e_t = y_t – E[y_t*], siguen una distribución normal con media cero y varianza desconocida, su probabilidad de ocurrencia estará dada por:

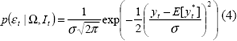
cuya función de verosimilitud se define como:

La maximización de (3) permite determinar el vector de parámetros W más probable para que los errores provengan de una distribución normal con media cero y varianza desconocida. Después de aplicar la función logaritmo natural a ambos lados de (3), y realizar algunas simplificaciones matemáticas se obtiene que:

donde K es una constante. Maximizar la ecuación anterior, implica minimizar la sumatoria de los errores al cuadrado, o en otras palabras, minimizar el error cuadrático medio (MSE) que es una medida muy común en el entrenamiento de modelos de redes neuronales:

4 PREDICCIÓN E INTERVALOS DE CONFIANZA

Al considerar la secuencia de observaciones y₁,…, y _T, y el MLP, la predicción para el periodo t+1, puede ser obtenida al reemplazar los términos correspondientes en la ecuación (1); por ejemplo, con P=1 se obtiene:

No obstante, y*_t+1 no es una cantidad numérica, ya que es et una variable aleatoria; en este caso y*_t+1 sigue la misma distribución de probabilidades de et. El pronóstico de y_t+h, con h>1, se obtiene como:

donde:

lo que implica que los pronósticos y*_t+h-1,…,y*_t+1 son requeridos como un insumo para calcular y*_t+h. La estimación numérica tanto de (6) como de (7) es simple en el caso de modelos lineales, y puede ser realizada directamente (Clements y Hendry, 1998); en el caso particular de los MLP (y en general para los modelos no lineales), este cálculo no puede ser realizado analíticamente, ya que:

1. Los errores e_t siguen una distribución empírica en la mayoría de los casos.
2. La ecuación (7) implica la suma de distribuciones empíricas, ya que la función g() en (1) induce una transformación no lineal sobre su entrada. Esto es ejemplificado en la Figura 2, donde se presenta la transformación inducida sobre la función de distribución de probabilidades de diferentes variables aleatorias normales con diferentes centros y la misma varianza, por el MLP que se presentan en la misma Figura. Para h=2, el cálculo de y*_t+2 implica sumar las variables aleatorias e_t+2 y la transformación de y*_t+1.

Figura 2. Transformación inducida por una función de transferencia sigmoidea bipolar a una función normal de distribución de probabilidades.
Figure 2. Induced transformation by a bipolar sigmoid transfer function on a normal probability distribution function.

4.1 Pronósticos puntuales

En los pronósticos puntuales, el objetivo es obtener una estimación de E[y*_t+h|I_t,W], tal que su estimador óptimo un periodo adelante (h=1) es definido por (6); este es calculado de forma similar a un modelo lineal. Para dos periodos adelante o más (h>1), el proceso se hace más complejo que en el caso de los modelos lineales, y se requiere realizar consideraciones adicionales.

4.1.1 Aproximación Ingenua

La aproximación más simple y directa que puede realizarse, es considerar que los errores futuros en el horizonte de predicción son cero; esto es: e_t+1 = e_t+2 = ••• = e_t+h = 0, tal que la predicción puede calcularse como:

La estimación se hace de forma progresiva, calculando primero y*_t+1, luego y*_t+2, y así sucesivamente.

El pronóstico obtenido se conoce como determínistico, siendo y*_t+h una variable discreta; el pronóstico determinístico es importante dentro del análisis de la dinámica del modelo, ya que puede indicar la divergencia de la secuencia de valores y*_t+1, y*_t+2,… Tal como lo indica Brown y Mariano (1989), este es un pronóstico sesgado ya que el valor esperado de y*_t+h, es diferente al obtenido al aplicar recursivamente (1).

4.1.2 Estimación directa

En esta aproximación, la distribución de probabilidades de y*_t+h es obtenida en función de la información disponible I_t+h, como

donde p(I_t+h|W) es una distribución condicional de probabilidades; véase a Tong (1990). La estimación numérica de la ecuación anterior, implica la estimación secuencial de las distribuciones de y*_t+1, y*_t+2, … usando métodos numéricos.

4.1.3 Método del error de predicción normal

Pemberton (1987) sugiere la estimación de y*_t+h bajo la suposición de que los errores et+ , e_t+2 ,… e_t+h-1 siguen una distribución normal con media cero y varianza s2h-1.

4.1.4 Método de Monte Carlo

La estimación de E[y*_t+h|I_t,W], es realizada usando (14) mediante el método de Monte Carlo, teniendo en cuenta que

pero que a su vez, y*_t+h-1 es condicional de sus valores pasados:

Para ello, se asume que los errores e_t+1 , e_t+2 ,… e_t+h-1 siguen una distribución normal con media cero y varianza conocida, la cual es calculada usando (3). Para obtener y*_t+h a partir de (16), la estimación se hace de forma progresiva, calculando primero y*_t+1, luego y*_t+2, y así sucesivamente. Su principal crítica es que los residuales no siguen exactamente una distribución normal, y por tanto, el valor calculado puede ser significativamente diferente del real.

4.1.5 Cálculo usando Bootstraping

La ventaja de este método (Efron & Tibshirani, 1993), es que no se realizan suposiciones sobre la distribución de probabilidades de los errores. Para estimar (16) la secuencia de errores e_t+1 , e_t+2 ,… e_t+h es obtenida a partir del muestreo de los residuales del modelo e₁ , e₂ ,… e_T obtenidos durante al etapa de estimación de los parámetros W.

4.2 Estimación de Intervalos de Confianza

El pronóstico puntual es poco informativo si no contiene información sobre sus intervalos de confianza; véase a Chatfield (1993). Ya que la distribución de probabilidades de y*_t+h es empírica, varias aproximaciones han sido sugeridas para la estimación de dichos intervalos. Las tres aproximaciones que se describen a continuación son idénticas cuando la distribución de es simétrica y unimodal, pero pueden diferir considerablemente ante distribuciones empíricas, tal como es anotado por Hyndman (1995).

4.2.1 Intervalo simétrico

Este método se fundamenta sobre la suposición de que la distribución de probabilidades de y*_t+h es normal, y que consecuentemente, los intervalos para una confianza a se obtienen de forma tradicional (simétricamente) alrededor de la media (pronóstico puntual).

4.2.2 Estimación de los cuartiles

A partir de una muestra de y*_t+h o su distribución de probabilidades, se calculan los puntos correspondientes a los cuartíles a/2 y (1- a/2).

4.2.3 Estimación de la región de densidad superior

Las regiones de densidad superior están conformadas por aquellos puntos y*_t+h tales que su función de probabilidad es superior a un valor ß tal que la probabilidad es igual a 1-a:

Hyndman (1996) sugiere varias técnicas para la presentación de regiones de densidad superior.

5 DIRECCIONES DE INVESTIGACIÓN

5.1 Propiedades ante muestras pequeñas

Una de los supuestos en que se basa la estimación de los parámetros de los perceptrones multicapa, es la normalidad de la distribución de los residuales. Usualmente, las pruebas de normalidad, tales como las de Lin-Muldhockar (1980) o Jarque-Bera (1987), podrían ser usadas para probar dicha hipótesis; sin embargo, es sabido de su falta de poder en muestras pequeñas; igualmente es bien sabido, que los estimados de los intervalos de confianza son extremadamente sensitivos a cualquier violación menor de la suposición de normalidad (Bonnet, 2006).

En el caso de los pronósticos para un horizonte superior a un periodo de tiempo, poco se ha investigado sobre los efectos del tamaño de la muestra sobre la precisión de la estimación; y es necesario considerar este tema, debido a la importancia práctica de este tipo de pronóstico.

5.2 Predicción sobre la distribución de probabilidades de y*_t+h

La predicción de series económicas y financieras es una de las principales aplicaciones de los MLP, debido a sus no linealidades; sin embargo, la estimación de la distribución de probabilidades de y*_t+h ha venido cobrando importancia para la implementación de estrategias de cubrimiento de riesgo.

Los métodos aquí descritos, han sido empleados en diferentes aproximaciones, como técnicas que permiten refinar la exactitud de los cálculos. No obstante, no es claro si ellos pueden ser usados de una forma segura cuando h es un valor relativamente grande; tampoco hay estudios que establezcan su desempeño ante la verdadera distribución de probabilidades, y si es necesario usar técnicas más sofisticadas basadas en MCMC (Monte Carlo Markov Chains) para obtener resultados más acordes con la realidad.

5.3 Uso de funciones de error alternativas

El uso del MSE como un criterio de ajuste entre los datos y el modelo, tiene varias ventajas desde el punto de vista estadístico; entre ellas se encuentran: la base teórica para la estimación de la distribución de probabilidades del vector de parámetros W, así como la distribución teórica de los residuales del modelo.

Sin embargo, esta no es la única medida de error posible, y en la literatura de redes neuronales se han usado otros criterios como la minimización del error absoluto o del error medio relativo (Masters, 1993). Se desconocen las propiedades de las distribuciones de probabilidades de los residuales para estas funciones, y si existen sesgos en la estimación de los intervalos de confianza y valores esperados para los pronósticos obtenidos con ellos.

5.4 Inclusión de la incertidumbre de los parámetros

En la estimación de y*_t+h se asume que W es conocido, sin tener en cuenta la incertidumbre asociada a los parámetros del modelo. Particularmente, Reeves (2005) ha realizado una propuesta para la construcción de intervalos de confianza para modelos ARCH basada en Bootstrapping. Debe investigarse la metodología propuesta puede ser aplicada a los MLP directamente, o que modificaciones debe realizarse.

5.5 Efecto de las transformaciones sobre la variable

Un paso obligado en el modelado y la predicción usando MLP, es el preprocesamiento de la serie temporal, especialmente con algún tipo de transformación de potencia en el caso de series económicas y financieras (Pascual et al, 2005). En este caso, la predicción óptima obtenida para y*_t+h es desarrollada para la serie transformada, y no es el mejor predictor, en términos estadísticos, para la serie real.

Es necesario desarrollar metodologías que permitan tener en cuenta, los sesgos causados en la predicción por las transformaciones inversas cuando la serie real ha sido preprocesada.

6 CONCLUSIONES

En este artículo, se han resumido las principales aproximaciones para la estimación de la predicción puntual y sus intervalos de confianza asociados para modelos basados en perceptrones multicapa. Nuestra investigación nos lleva a concluir, que si bien, hay un desarrollo importante sobre este tópico particular, aún quedan preguntas importantes que deben ser solucionadas, las cuales ha sido direccionadas en este documento. Sin embargo, ellas no demeritan en ningún sentido los progresos que se han desarrollado en esta área.

BIBLIOGRAFÍA        [ Links ]
[2] BROWN, B.Y. & MARIANO, R.S. 1989. Predictors in dynamic nonlinear models: large sample behaviour. Econometric Theory 5, 430-452.         [ Links ]
[3] CHATFIELD, C. (1993). Calculating interval forecasts (with discussion). Journal of Business and Economic Statistics, 11, 121– 135.         [ Links ]
[4] CLEMENTS, M.P., FRANCES, P.H, & SWANSON, N.R. 2004. Forecasting economic and financial time-series with non-linear models. International Journal of Forecasting, 20, pp 168-183         [ Links ]
[5] EFRON, B. Y TIBSHIRANI, R. (1993), An Introduction to the Bootstrap, Chapman & Hall.         [ Links ]
[6] HYNDMAN, R.J., 1995. Highest-density forecast regions for nonlinear and nonnormal time series. Journal of Forecasting 14, 431-441         [ Links ]
[7] HYNDMAN, R.J. 1996. Computing and graphing highest-density regions. American Statistician 50, 120-126.         [ Links ]
[8] JARQUE, C. Y BERA, A. 1987. A test for normality of observations and regression residuals, International Statistical Review (55), 163–172.         [ Links ]
[9] LIN, C.C & MUDHOLKAR, G.S. 1980. A simple test for normality against asymmetric alternatives. Biometrika, 67, 455-461.         [ Links ]
[10] MASTERS, T. (1993), Practical Neural Network Recipes in C++, first edn, Academic Press, Inc.         [ Links ]
[11] MASTERS, T. (1995), Neural, Novel and Hybrid Algorithms for Time Series Prediction, first edn, John Wiley and Sons, Inc.         [ Links ]
[12] PASCUAL, L, ROMO, J, & RUIZ, E. 2005. Bootstrap prediction intervals for power-transformed time series. International Journal of Forecasting, 21, 219– 235         [ Links ]
[13] PEMBERTON, J. 1987. Exact least squares multi-step prediction from nonlinear autoregressive models, Journal of Time Series Analysis, 8, 443-448.         [ Links ]
[14] REEVES, J.J. Bootstrap prediction intervals for ARCH models. International Journal of Forecasting, 21, 237– 248         [ Links ]
[15] TONG, H. (1990), Non-linear Time Series, a dynamical system approach, Oxford Statistical Science Series, Claredon Press Oxford.         [ Links ]