Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
DYNA
Print version ISSN 0012-7353On-line version ISSN 2346-2183
Dyna rev.fac.nac.minas vol.74 no.151 Medellín Jan./Apr. 2007
HIPERELASTICAS
SPRING–PARTICLE MODEL FOR HYPERELASTIC
CLOTH
MANUEL GARCÍA
EAFIT University, Medellin, Colombia. Department of Mechanical Engineering, mgarcia@eafit.edu.co
MARIO GÓMEZ
EAFIT University, Medellin, Colombia. Department of Mechanical Engineering, mgomezbo@eafit.edu.co
OSCAR RUIZ
EAFIT University, Medellin, Colombia. Department of Mechanical Engineering, oruiz@eafit.edu.co
PIERRE BOULANGER
University of Alberta, Alberta, Canada, Department of Computing Science, pierreb@cs.ualberta.ca
Recibido para revisar 5 de Abril de 2006, aceptado 11 de Julio de 2006, versión final 11 de Septiembre de 2006
RESUMEN: Este artículo presenta un modelo computacional para la simulación de telas hiperelásticas. El modelo propuesto tiene un enfoque multi-partículas y simula la interacción de un material textil con un objeto deformante. La tela está representada por mallas rectangulares compuestas por resortes, este hecho permite al modelo comportarse ortotrópicamente y en consecuencia es posible simular sus propiedades en ambos sentidos. Las relaciones constitutivas del material preservan las capacidades hiperelásticas naturales de la tela. En el modelo desarrollado aquí, inicialmente la tela se encuentra en su estado natural no deformado. Luego se le da una deformación inicial que garantice el no contacto o intersección con el objeto deformante. Finalmente, la tela deformada es liberada, en consecuencia ella comienza a moverse iterativamente hacia a una posición de equilibrio. La posición final de equilibrio es alcanzada cuando las fuerzas internas son balanceadas por las fuerzas externas de contacto causadas por el objeto. Esto se logra cuando el criterio de parada ha sido satisfecho.
PALABRAS CLAVE: Material hiperelástico, Modelo multi- partículas, Comportamiento no lineal.
ABSTRACT: This article presents a computational model to simulate the deformation of hyperelastic fabrics. The model is based on a spring-particle approach and it simulates the interaction of a textile tissue with a forming body. The fabric is represented by rectangular meshes of springs. This fact enables the model to behave orthotropically and therefore it is possible to simulate the warp and weft properties. The constitutive relations preserve the natural hyperelastic capabilities of the cloth. In the model developed herein, initially the cloth lies in its relaxed un-deformed state. Then it is given an initial deformation that guarantees no contact nor intersection with the forming rigid body. Finally, the deformed cloth is realised, and moves iteratively towards an equilibrium location. The final equilibrium location is reached when the internal forces are balanced by the external contact forces caused by the rigid object. This is achieved when the stop criterion has been satisfied.
KEY WORDS: Hyperelastic material, Spring-particle model, Non–linear behavior.
1. INTRODUCTION
Hyperelasticity is the capability of a material to experience large elastic strain due to small forces without losing its original properties [8]. A hyperelastic material has non-linear behavior,
which means that it does not deform in a linear relationship with the applied stress. Several woven fabrics like Lycra® and Nylon® have hyperelastic behavior and are widely employed by textile companies. Existing cloth simulation models are, in most cases, good enough for visualization purposes and usually aim to model the drape of fabric materials where rotational (bending) deformation is large and membrane deformation is very low. This study uses multi-particle methods and is intended to simulate fabrics under stretching conditions. This situation is typical of garments such as underwear and T-shirts which are usually made of materials such as spandex or Lycra®. In these garments, the stretch forces are very large compared to the weight of the cloth or the bending forces.
2. LITERATURE REVIEWBreen, House, and Wozny [4] defined a fabric as a complex mechanical mechanism composed of woven threads into an interlocking network. The geometric relations where the threads of the mechanism (fabric) cross each other are the basis of Peirces model [18]. Peirce is considered a pioneer in cloth modeling [5]. The fact that Peirces model is inherently geometric makes it applicable to limited problems. In 1954, Love [14] found a graphical solution to the non-linear equations proposed by Peirce. Four years later Kemp [12] modified the equations proposed by Peirce assuming yarn cross sections as elliptical instead of circular, achieving better results. The first three-dimensional Peirce-like model was proposed by Kawabata, Niwa, and Kawai [11]. This model uses experimental data obtained from laboratory tests.
Another area explored in cloth modeling has been the application of the theory of elasticity. Some authors like Kilby [13] proposed a model with rectilinear elements joined at the intersecting points of the fabric. The behavior of every element was based on the theory of elasticity for small displacements. Via linear stress-strain relationships, this theory deals with the problem of finding the final state of a body due to the application of external forces. However, cloth modeling requires expressions which are inherently non-linear. That is the reason why in 1996 Ascough, Bez, and Bricis [1] took the non-linear concept and developed a new approach based on Kilbys model. This model is composed of a mesh of simple beam elements with non-linear behavior. In general, when attempting to solve these kind of equations, iterative algorithms are used where the stiffness matrix of the system is updated at each iteration. In reference [15], Malvern states the basic concepts of the theory of elasticity for large displacements. Based on those concepts, Bathe [2] and Crisfield [6] introduce the Finite Element Method applied to problems where large displacements, large rotations and large strains are required, which are the usual requirements in cloth modelling.
Due to the limitations of the classical theory of elasticity some authors like Mooney [16] and Ogden [17], proposed a new method based on a strain energy function that defines a material which experiences large deformations (cloth, woven fabrics, hyperelastic materials, etc). This function is minimized to achieve a final equilibrium state. Usually the strain energy function has three main components: i) tension, ii) bending, and iii) shearing. Spring-force formulations appeared in 1988 with the Haumann and Parent model [10], and to this date numerous spring-force models have been published. In these types of models the interactions between the intersection points of the fabric are not modeled using elastic properties. Instead these interactions are described by spring forces. Gudukbay, Ozguc, and Tokad [9] worked with these types of models and obtained accurate visual results. In 1995 Provot [19] described a model with three different kinds of springs: i) a structural tension spring, ii) a shear spring, and iii) a flexion spring. If dynamic variables are added to the springs, then it is possible to simulate cloth movement [5]. This type of model seeks for a final position via an iterative algorithm which searches for the equilibrium of external and internal forces. In 1994 Breen, House, and Wozny [4] proposed a similar model, but instead of springs the interactions among particles are described via energy functions.
Most cloth models avoid the frictional forces which are present in the interaction between a fabric and an object. This fact has been considered by Yamamoto and Imaoka [22] to obtain more accurate results. Their model takes into consideration that the final shape of the fabric depends on the frictional coefficient as well as the location of the rigid object and the history of changing locations.
The model proposed in this article is a spring-force formulation. It is developed for fabrics which behave hyperelastically, and elongation is the prevalent source of deformation. These situations are typically found in the manufacturing process, thermoforming of fabrics, or when wearing garments that wrap around the body.
3. THE NON-LINEAR PURE-TENSION SPRING-ELASTIC MODELIn multi-particle methods, balance of forces at each particle leads to the following equation
![]()
where Fr is the resulting force at the particle, W is the gravity load over a particle, and Fseams is the sewing force [7].
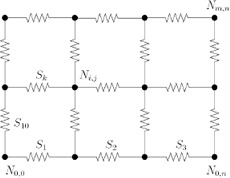
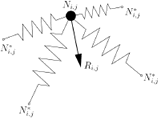
Consider a rectangular piece of woven fabric to be partitioned into an array of points named nodes, numbered from left to right and from bottom to top as shown in Figure 1 and stored in matrix N of dimension n x m. Beside the point location, every node Ni,j has information about the springs connected to the nodes, its movement restriction, and information about how the node is in contact with the surface of a forming rigid object.
Figure 1: Numbering nodes and springs on the grid.
The links between nodes are represented by spring forces Sk, which are 3–D vectors Sk R3. Those vectors are numbered consecutively from left to right and from bottom to top as shown in Figure 1 and stored in a vector F of dimension 1xa. F = [S1 , S2 , , Sk , , Sa], where a is the total number of springs within the grid. The overall system with nodes and springs is referred to as a grid in this study.
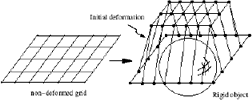
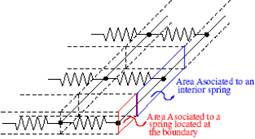
3.1 MethodologyInitially the grid lies on a plane p and the springs are at equilibrium due to the absence of external forces. Constraints are defined (or applied) to a set of nodes in the grid. Then, the grid is given an initial deformation. This deformation should guarantee no contact or intersection with the forming rigid body, see Figure 2. Next, the grid is realised, and it begins to move seeking for an equilibrium location where the forces at the nodes are balanced. Each spring of the grid produces a force Sk which is a function of the stress s, and the associated area Ak as shown in Figure 3. Furthermore, the orientation of a spring force Sk is given by a unitary vector F, that can be calculated from the coordinates of the nodes which connect the spring k in the grid.
Figure 2: Deformed grid and the rigid object.
Figure 3: Areas associated to the springs.
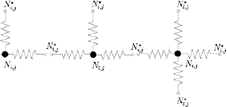
Every node Ni,j of the grid experiences a set of forces caused by the surrounding springs. The possible configurations for a node are shown in Figure 4.
Figure 4: Possible configurations of the interactions between springs. Two, three and four springs configurations.
Any configuration of springs from Figure 4 is joined at a node Ni,j, which has been referred to as a join node. The rest of them have been named as opposite nodes Ni,j*. Hence F is given by .
![]()
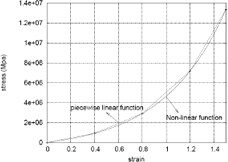
To represent the stretch and warp properties of the fabric, the grid has different material properties along the x and y axes. These are represented by a stress–strain non–linear function s(e), s:R?R. This non–linear stress-strain function s(e) is obtained from a laboratory test and is approximated by a piecewise linear function as shown in Figure 5. The grid movement is an iterative process. The coordinates of the every node Ni,j at iteration t are updated according to the rules of node movement exposed in Section 3.2 until a local equilibrium is achieved, producing a new state at iteration t + 1. Also, an evaluation of the contact of the Ni,j node with the rigid object is undertaken from iteration t to iteration t + 1.
Figure 5: Approximation of the original non-linear function into a piecewise linear function.
3.2 Node Movement
Once the initial grid is deformed, every node Ni,j experiences a resultant force Ri,j R3. Force Ri,j pushes node Ni,j towards a local equilibrium position, and it is given by the summatory of all the forces Sk which surround node Ni,j, that is
![]()
The procedure to move a node Ni,j to its local equilibrium position consists of moving the node in the direction of Ri,j by a small amount, then reassess Ri,j and move the node Ni,j until the magnitude of the resultant force becomes zero (¦Ri,j¦ = 0). The amount of movement in the Ri,j direction is defined by the step size ?, which is a scalar value. Hence, selecting an appropriate value for ? that guarantees a relaxation of the system (¦Ri,j ¦? 0) becomes a main task on the model.
The criteria chosen to compute the ?-value is an average of the deformations of each spring which surrounds node Ni,j. Initially, the deformation d of a spring k is defined as the difference between the stretched length lst of spring k and its unstretched length lun, then .
![]()
Once dk has been computed, the step size ? for node Ni,j at iteration t is defined as ,
![]()
where C is a constant defined by the user. At every iteration the grid gets closer to its final equilibrium position, and for that reason the value of ? also needs to be adequate to guarantee convergence. Depending on the value of ?, the grid instead of being relaxed could be taken away from the equilibrium state. Therefore, the algorithm evaluates at every iteration if the step size ?i,j calculated by Equation (4) is appropriate to relax node Ni,j, that is ¦Ri,j ¦? 0. Otherwise, ? has to be recalculated and reevaluated iteratively until a suitable value is obtained. It means that if the ?-value initially calculated is inappropriate, then ? will be consecutively divided by C until the step size becomes good enough for the relaxing purposes. Thus the value of C depends on how much the user wants to effect the step size at each iteration.
The new location of node Ni,j generated by force Ri,j is given by
![]()
Depending on the constraints imposed by the rigid body, the movement of Ni,j can be classified as: (i) free, (ii) restricted by the surface of the rigid object, and (iii) constrained by the initial boundary conditions.
3.2.1 Free Movement
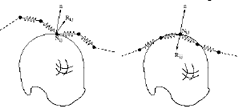
Nodes involved in this type of movement do not have any restriction. They are not in contact with a rigid object, neither are they constrained by the boundary conditions. They can move freely in the 3–D space in the direction of vector Ri,j (see Figure 6).
Figure 6: Free Movement.
At iteration t a specific node Ni,j can move freely, but at iteration t + 1 it could be restricted by the surface of the rigid object.
3.2.2 Movement Restricted by the Surface of the Rigid Object
The spring-elastic model being studied takes into account tension (internal forces) between the particles of the fabric. These forces are balanced by the external forces applied due to contact with rigid object. Due to the nature of the simulation, bending and shear do not play an important role. Furthermore friction between the woven fabric and the surface is out of the scope of this study.
If at iteration t a node Ni,j is in contact with the surface of the rigid object, it can experience two kinds of movement depending on the direction of the resultant force Ri,j. When the resultant force at a node Ni,j over the surface points towards the outside of the object, that is n Ri,j > 0, then the node moves in the direction of Ri,j and is free of contact with the surface (see Figure 7a).
Figure 7: Movement restricted by the surface of a rigid object.
On the contrary, when the resultant force Ri,j points towards the inside of the forming rigid object, that is n Ri,j < 0, then node Ni,j moves over the surface (see Figure 7b).
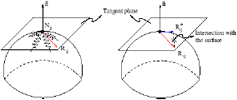
The node Ni,j whose movement is over the surface, gets its local equilibrium when the component Ri,j* of the vector Ri,j over the tangent plane to the surface at the contact point is zero. The node is moved in the direction of the component Ri,j* until this condition is achieved. When this occurs, the position of the node Ni,j in the tangent plane is projected over the surface to get the final location of the node (see Figure 8).
Figure 8: Movement over the surface. The force vector Ri,j over a node Ni,j in contact with the surface is projected over a tangent plane to obtain Ri,j* .
3.2.3 Constrained Movement
The movement in the x, y, and z axes of some specific nodes can be constrained. Any node movement can be restricted in one or more axis. When a node Ni,j is constrained, Equation (5) only takes into account movement along the non–restricted axis.
3.3 Convergence Criterion eLet V Rs be a vector of dimension s = n x m, with the total number of nodes in the grid. If k is a number that maps the indexes of a node Ni,j, as (i - 1)n + j, then V is defined as
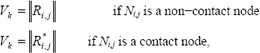
that is, Vk contains the magnitude of the resultant force Ri,j in the nodes at iteration t. If node Ni,j is in contact with the rigid body then Vk contains the magnitude of the projection over the surface Ri,j* instead.
The grid will be in theoretical equilibrium when V = 0. Then, the convergence criteria can be defined as .
![]()
The infinity-norm of vector V is less or equal than e R.
4. EXPERIMENTS AND RESULTSThis section presents two application examples of the spring–particle model for hyperelastic cloth. The first one consists of a simulation of contact between a fabric and a non-convex forming mold. The second one simulates the contact between a fabric and a womans torso.
To perform the simulation properly, it is necessary to provide the spring-particle model with the following: i) the geometry of the rigid forming object, ii) the dimensions of the textile, as well as the number of divisions for each side of the rectangle, iii) the warp and weft properties, iv) the constrained nodes, and v) an initial deformation which guarantees no contact or intersection with the forming rigid body.
The geometry format consists of a list of points Pi = (ni,xi,yi,zi), where ni is the index number for point Pi; followed by a list of triangles tj = (n1,n2,n3)j, where n1, n2 and n3 are the indexes of the points which conform triangle j. The constitutive material properties in the warp and weft directions of the fabric are described by a piecewise linear function. That is, a list of points Mp = (sp,ep) which describe the function.
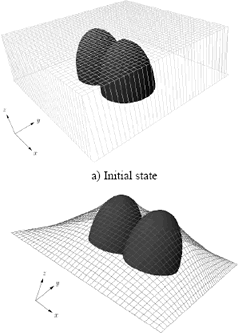
In the first example a non-convex 3-D thermoforming mold was employed as the forming object (see figure 9). This geometry was generated in CAD software and exported into a text file with the format required by the model. The fabric used was 10cm long by 10cm wide and 40 divisions were taken on each side. The material was considered isotropic; hence warp and weft properties were the same. Those properties were obtained via experimental tests developed at EAFIT University and ICIPC Institute [21]. All the nodes in the perimeter of the fabric were constrained in the x, y, and z axes. The nodes which do not belong to the perimeter were moved in the z direction up to a location where no contact with the non-convex object was guaranteed. Figure 9 shows the initial and the final state of the interaction of a fabric with the thermoforming mold.
Figure 9: Interaction between a thermoforming mold and a woven fabric.
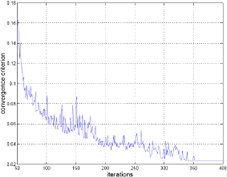
The stop criterion was satisfied after 360 iterations, see figure 10. The value for the stop criterion was e = 2.4e-2 Newtons (N). The simulation results show that the fabric wraps over the contact area of the forming object according to what is usually seen in real situations. No experimental data was found in the literature in order to validate this simulation. Therefore, further research in this direction must be accomplished. At the first 50 iterations the stop criterion has values between 10N and 8N. Those values correspond to some springs that are too stretched to achieve the initial state location of the fabric, see figure 9a. Those springs are rapidly relaxed by the model. Therefore, after iteration 50 all the springs within the grid begin with and slower relaxation process until the stop criterion is achieved, see figure 10.
Figure 10: graph of the convergence criterion (Newton) vs. number of iterations
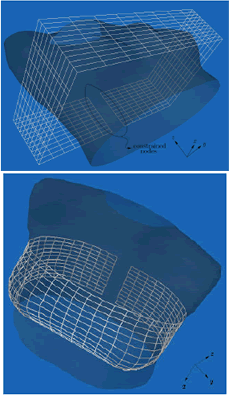
In the second simulation, a womans torso was digitalized. Then, a surface which approximates the cloud of points obtained in the digitalization process was generated. The fabric used for the simulation was 50cm long by 20cm wide. 40 divisions were taken on its long side and 10 divisions on its wide side. The material was also considered isotropic with the same properties used in the previous example. All the nodes belonging to the perimeter wide side of the fabric were constrained on the x and y axes, see figure 11a. Therefore constrained nodes where allowed to move along z axis. Initially, the fabric was deformed to surround the torsos surface without touching it. As the location of the fabric generated is a non-equilibrium state, it will deform until the resulting forces at the nodes are minimized.
Figure 11: Interaction between womans torso and a woven fabric.
The simulation stopped after 300 iterations. The value for the stop criterion was e = 1e-4 N.
5. CONCLUSIONSA spring–particle formulation to model hyperelastic fabrics is proposed. Simulation of the interaction between a non–linear material and a rigid object is achieved. The model is composed of rectangular meshes of springs which represent the fabric. This fact enables the model to behave orthotropically. Taking advantage of this capability it is possible to simulate the warp and weft properties of the fabric.
The material behavior of the fabric is described by constitutive equations which have hyperelastic capabilities. This non–linear stress-strain relationship is obtained from a laboratory test and is approximated by a piecewise linear function. The rigid object is represented by a full boundary representation geometry (Full B-Rep) composed of triangles. The Full B-Rep geometry is gotten from any CAD software which has the capabilities of exporting in VRML or VTK formats. The deformation model is based on an iterative procedure which seeks for an equilibrium location of the grid which represents the fabric (cloth). The final equilibrium position is achieved when the internal forces are balanced by the external contact forces caused by the rigid object. This is gotten by relaxing every node locally within the grid at each iteration. As a result of these local relaxations a global relaxed state for the whole grid is reached after the convergence criterion has been obtained.
REFERENCES
[1] ASCOUGH, J., H.E. BEZ, A.M. BRICIS, A simple beam element, large displacement model for the finite element simulation of cloth drape, Journal of the Textile Institute, 87, 152–165, 1996. [ Links ]
[2] BATHE, KLAUS JURGEN, Finite Element Procedures, Prentice-Hall Inc., USA, 1996. [ Links ]
[3] BLATZ, P.J., W.L. Ko, Application of finite elastic theory to the deformation of rubbery materials, Transactions of the Society of Rheology, VI, 223–252, 1962. [ Links ]
[4] BREEN, D., D. HOUSE, AND M. WOZNY, Predicting the drape of woven cloth using interactive particles, SIGGGRAPH-94, 365–371, 1994. [ Links ]
[5] BREEN, DAVID E., A survey of cloth modeling methods, Cloth modeling and animation, 19–53, 2000. [ Links ]
[6] CRISFIELD, M.A., Non-linear Finite Element Analysis of Solids and Structures, John Wiley & Sons, England, 2001. [ Links ]
[7] EISCHEN, J., R. BIGLIANI. Continuum versus Particle Representations, In: Cloth Modeling and Animation (Eds Donald H. House and David E. Breen), A.K. Peters Publishing, 2000. [ Links ]
[8] FAGAN, M. J., Finite Element Analysis: Theory and Practice, Longman Group UK Limited, Malaysia, 1992. [ Links ]
[9] GUDUKBAY, U., BULENT OZGUC, YILMAZ TOKAD, A spring force formulation for elatically deformable models, Computer and Graphics, 21, 335–346, 1997. [ Links ]
[10] HAUMANN, D.R., R.E. PARENT, The behavioral test bed: Obtaining complex behavior from simple rules, The Visual Computer, 4, 332–347, 1988. [ Links ]
[11] KAWABATA, S., M. NIWA, H. KAWAI, The finite-deformation theory of plain-weave fabrics, Journal of the Textile Institute, 1973. [ Links ]
[12] KEMP A., An extension of Peirces cloth geometry to the treatment of non-circular threads, Journal of the Textile Institute, 49, 1958. [ Links ]
[13] KILBY, W.F., Planar stress-strain relationships in woven fabrics, Journal of the Textile Institute, 54, 1963. [ Links ]
[14] LOVE, L., Graphical relationships in cloth geometry for plain: twill and sateen weaves, Textile Research Journal, 1954. [ Links ]
[15] MALVERN, LAWRENCE E., Introduction to the mechanics of a continuous medium, Prentice-Hall Inc., USA, 1969. [ Links ]
[16] MOONEY, M., A theory of large elastic deformation, Journal of Applied Physics, 11,582–592, January 1940. [ Links ]
[17] OGDEN R.W., Large deformation isotropic elasticity on the correlation of theory and experiment for incompressible rubberlike solids, Proc. R. Soc. Lond. A., 1972. [ Links ]
[18] PEIRCE, F.T., The geometry of cloth structure, Journal of the Textile Institute, 28, 1937. [ Links ]
[19] PROVOT, X., Deformation constraints in a mass-spring model to describe rigid cloth behavior, Proc. Graphics Interface, 147–154, 1995. [ Links ]
[20] RIVERA, ANDRES M., De lo discreto a lo continuo en el modelamiento de membranas. Matematicas: Ensenanza Universitaria, XII, 3–19, 2004. [ Links ]
[21] RUIZ, O., GARCIA M. Modelamiento geometrico y termico de moldes de termoformado para textiles. Reporte proyecto de investigacion. Universidad EAFIT. 2003. [ Links ]
[22] YAMAMOTO, I., HARUKI IMAOKA, Implementation of friction model in cloth simulation system, Seni Gakkaishi, 59, 358-364, 2003. [ Links ]