Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
DYNA
Print version ISSN 0012-7353On-line version ISSN 2346-2183
Dyna rev.fac.nac.minas vol.74 no.151 Medellín Jan./Apr. 2007
HEURÍSTICOS PARA RESOLVER EL PROBLEMA DE
PLANEACIÓN DE TAREAS CON RESTRICCIÓN DE
RECURSOS (RCPSP)
A COMPARATIVE ANALYSIS BETWEEN TWO
HEURISTIC ALGORITHMS FOR SOLVING THE RESOURCE-
CONSTRAINED PROJECT SCHEDULING PROBLEM
(RCPSP)
LUIS FERNANDO MORENO
Facultad de Minas, Universidad Nacional de Colombia-Medellín, lfmoreno@unalmed.edu.co
FRANCISCO JAVIER DÍAZ
Facultad de Minas, Universidad Nacional de Colombia-Medellín, javidiaz@unalmed.edu.co
GLORIA ELENA PEÑA
Facultad de Minas, Universidad Nacional de Colombia-Medellín, gepena@unalmed.edu.co
JUAN CARLOS RIVERA
Facultad de Ingeniería, Universidad de Antioquia-Medellín, rivera@udea.edu.co
Recibido para revisar 1 de Septiembre de 2005, aceptado 13 de Marzo de 2006, versión final 8 de Noviembre de 2006
RESUMEN: El Problema de Planeación de Tareas con Restricción de Recursos, RCPSP, ha sido estudiado mediante técnicas analíticas que garantizan una solución óptima, aunque en la práctica resultan no viables por su alto tiempo de procesamiento. Por ello, se utilizan algoritmos heurísticos, los cuales, aunque no garantizan un óptimo, pueden entregar resultados satisfactorios en tiempos considerablemente menores. Los heurísticos más utilizados para solucionar el RCPSP son Enfriamiento Simulado, Búsqueda Tabú, Algoritmos Genético y Grasp, ya que por su flexibilidad permiten variaciones en su forma específica de aplicación. En el presente artículo se introducen dos variaciones para mejorar la eficiencia de los algoritmos de Búsqueda Tabú y Enfriamiento Simulado, las cuales son la utilización de la cota inferior conocida como LBS y la propuesta por los autores denominada estrategia de duraciones mínimas.
PALABRAS CLAVE: Programación de tareas, Heurísticos, Búsqueda tabú, Enfriamiento, Simulado, RCPSP, Duraciones mínimas, Cota inferior.
ABSTRACT: The Resource-Constrained Project Scheduling Problem, RCPSP, has been studied by means of analytical techniques that guarantee an optimal solution, although actually are nonviable due to the high processing time. For that reason, heuristic algorithms are used, that, although do not guarantee an optimal solution, can give satisfactory results in considerably less time. The heuristic algorithms more used to solve the RCPSP are Simulated Annealing, Taboo Search, Genetic Algorithms and Grasp, since by its flexibility they allow variations in the specific form of application. In the present paper two variations are introduced to improve the efficiency of the algorithms Taboo Search and Simulated Annealing, which are the use of the lower bound known as LBS and the denominated strategy of minimal durations proposed by the authors.
KEYWORDS: Task programming, Heuristic, Taboo search, Simulated annealing, RCPSP, Minimal durations, Lower bound.
1. INTRODUCCIÓN
El problema de programación de tareas o scheduling puede definirse de manera muy general como el problema de organizar o secuenciar una serie de operaciones y ubicarlas en el tiempo sin violar ninguna de las restricciones, de precedencias y recursos, impuestas en el sistema. Existen dos estrategias para resolver el problema de scheduling: los algoritmos analíticos que garantizan la solución óptima, algunos de los cuales se encuentran en [1] y [2]; y los algoritmos heurísticos que aunque no garantizan la solución óptima, sí producen soluciones aproximadas al óptimo, en la mayoría de los casos, en tiempos considerablemente menores.
El presente trabajo tiene como objetivo mostrar y comparar los resultados obtenidos en el estudio de uno de los problemas más tratados en el área del scheduling: el Resource-Constrained Project Scheduling Problem, denominado RCPSP, utilizando los métodos heurísticos de Enfriamiento Simulado y Búsqueda Tabú, para cada uno de los cuales se presenta un programa de computador en Visual Basic versión 6.0, que trabaja con una nueva Estrategia de Duraciones Mínimas, propuesta por los autores, la cual se explica en el numeral 6 del presente artículo.
2. DEFINICIÓN DEL PROBLEMA DE PLANEACIÓN DE TAREAS CON RESTRICCIÓN DE RECURSOS: RCPSP
Se tiene un conjunto X de n actividades y m recursos, donde cada recurso k (k = 1, ,m) tiene una disponibilidad bk en cada unidad de tiempo. Cada actividad i (i = 1, ,n) tiene una duración di, y su ejecución requiere una cantidad constante rik del recurso k en cada unidad de tiempo. Todas las cantidades di, rik y bk son números enteros no negativos. Cada actividad j esta asociada a un conjunto de predecesores inmediatos: actividades que deben ser completadas antes de comenzar la ejecución de la actividad j. Las actividades están
topológicamente ordenadas, es decir, cada predecesora de la actividad j tiene un número de actividad más pequeño que j [3]. El objetivo del RCPSP es asignar tiempos de inicio a cada una de las actividades de manera que se satisfagan todas las restricciones, de precedencias y recursos del sistema, y se minimice la duración total del proyecto o makespan.
3. FORMULACIÓN MATEMÁTICA
La forma simple tradicional de plantear el RCPSP que se describió en el numeral anterior, mediante programación entera es presentada por Mingozzi et al. [3]:
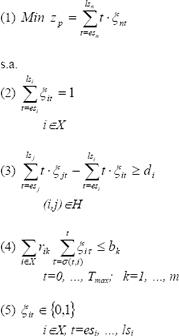
donde:
lsi = late start de la actividad i (tiempo de inicio más tardío).
esii = early start de la actividad i (tiempo de inicio más temprano).
xit = variable binaria, toma el valor 1 si y sólo si la actividad i empieza al principio del período t y 0 en caso contrario.
X = conjunto de actividades.
H = conjunto (i,j) de precedencias, donde (i,j) significa que i es predecesor de j.
rik = cantidad que la actividad i consume del recurso k durante su ejecución.
s(t,i) = max(0, t-di + 1).
bk = disponibilidad del recurso k (constante durante la duración del proyecto).
En este planteamiento siempre se consideran dos actividades artificiales (dummy jobs) que son la primera y la última (1 y n), con duración cero y con consumo cero de todos los recursos. El fin de estas actividades es representar el punto de inicio y el punto de terminación respectivamente, del proyecto.
La ecuación (1) es la función objetivo: makespan o duración total del proyecto.
Las ecuaciones (2) representan la restricciones de no interrupción (non-preemption), es decir, las que obligan a que una actividad debe continuarse hasta su terminación una vez iniciada.
Las ecuaciones (3) representan las restricciones de precedencia: una actividad solo puede iniciar una vez terminadas todas las predecesoras.
Las ecuaciones (4) representan las restricciones de recursos: en cualquier tiempo la cantidad de recursos utilizados por todas las actividades en ejecución no debe superar la disponibilidad de cada recurso correspondiente.
Aunque es fácil la solución del problema mediante cualquier programa de programación entera tal como CPLEX, lingo o lindo y también lo es la generación automática de todas las restricciones y la función objetivo en términos de las precedencias, los consumos de los recursos y sus disponibilidades, es notorio el deterioro del tiempo de ejecución cuando se incrementa el número de actividades. Cabe recordar que la dificultad del problema está más asociada con el número de actividades que con el número de recursos, pues son las actividades las que dan origen a la explosión combinatoria del problema.
Aunque las restricciones (2), (3) y (4) son fáciles de plantear, como se mencionó en el párrafo anterior, hay que tener presente que en cada conjunto de ellas pueden existir cientos y hasta miles para problemas no muy grandes. Por ello las versiones poco potentes de lingo y lindo no son en la práctica muy útiles para la solución del problema, desde el punto de vista de capacidad del paquete, adicional al ya mencionado problema del tiempo de ejecución.
El planteamiento de programación entera entonces es útil para entender en qué consiste el problema y obtener conclusiones teóricas. Sin embargo, existe una característica adicional del planteamiento de programación entera, y es el hecho de que permite la obtención de cotas inferiores, mediante la técnica de relajación (ignorar algunas restricciones). Sobre la utilidad de una cota inferior se hablará más adelante.
4. MÉTODOS HEURÍSTICOS
El modelo presentado en el numeral anterior puede ser resuelto con técnicas analíticas, como la programación entera, que garantizan una solución óptima, pero que en la práctica resultan no viables dado su nivel de complejidad y su alto tiempo de procesamiento [4]. Por lo tanto, es necesario recurrir a los denominados métodos heurísticos que aunque no garantizan soluciones óptimas, permiten una comprensión más intuitiva del problema y llegar a soluciones que usualmente resultan bastante cercanas al óptimo en tiempos considerablemente menores.
Los métodos heurísticos más utilizados para la solución del RCPSP son Algoritmos Genéticos, Grasp, Búsqueda Tabú y Enfriamiento Simulado. En el presente trabajo se utilizan la Búsqueda Tabú y el Enfriamiento Simulado, los cuales se describen a continuación.
El Enfriamiento Simulado fue propuesto por primera vez por Metrópolis et al. [5] y usado en optimización combinatoria por Kirkpatrick et al. [6]. Este heurístico se basa en los conceptos descritos originalmente por la mecánica estadística que describe el proceso físico sufrido por un sólido al ser sometido a un baño térmico.
Se sabe en ingeniería, que una manera de encontrar los estados de energía de sistemas complejos, tales como sólidos, consiste en utilizar la técnica de enfriamiento, en la que el sistema se calienta primero a una temperatura en la que sus granos deformados recristalizan para producir nuevos granos, y luego se enfría suavemente y de esta manera, cada vez que se baja la temperatura, las partículas se reacomodan en estados de más baja energía hasta que se obtiene un sólido con sus partículas acomodadas conforme a una estructura de cristal (estado fundamental). En la fase de enfriamiento, para cada valor de la temperatura, debe permitirse que el sistema alcance su equilibrio térmico [7].
De forma análoga, en el algoritmo de enfriamiento simulado los estados del sistema corresponden a las soluciones del problema, la energía de los estados a los criterios de evaluación de la calidad de la solución (generalmente se utiliza la función objetivo), el estado fundamental a la solución óptima del problema, los estados metaestables serán los equivalentes a los óptimos locales, y la temperatura está asociada a una variable de control. El éxito del Enfriamiento Simulado se basa en la escogencia de una buena temperatura inicial y una adecuada velocidad de enfriamiento [7].
La característica principal de este algoritmo es que al buscar una nueva solución Sn+1 dada una solución Sn, acepta en ocasiones una de inferior calidad a la de Sn por medio de una función probabilística la cual depende del parámetro variable de temperatura y de la calidad ofrecida por las dos soluciones Sn y Sn+1. Mientras más bajo sea el parámetro de temperatura, menor será la probabilidad de aceptar una solución peor, y viceversa [8].
La Búsqueda Tabú es un procedimiento iterativo para resolver problemas de optimización combinatoria de gran dificultad. Los orígenes de dicho procedimiento se remontan a los años 70, pero fue realmente en los trabajos de Fred Glover [9] donde se utiliza por primera vez el nombre de Búsqueda Tabú y se introduce la metodología general empleada por este procedimiento.
La Búsqueda Tabú puede ser utilizada para volver más agresivo cualquier procedimiento de búsqueda local. Para tal efecto, toma de la Inteligencia Artificial el concepto de memoria y lo implementa mediante estructuras simples con el objetivo de dirigir la búsqueda teniendo en cuenta la historia de ésta. Es decir, el procedimiento extrae información de lo sucedido hasta la solución actual y actúa en consecuencia. En este sentido puede decirse que hay un cierto aprendizaje y que la búsqueda es inteligente. El principio de la Búsqueda Tabú podría resumirse así:
Es mejor una mala decisión basada en información, que una buena decisión al azar, ya que, en un sistema que emplea memoria, una mala elección basada en una estrategia proporcionará claves útiles para continuar la búsqueda. Una buena elección fruto del azar no proporcionará ninguna información para posteriores acciones [11].
5. COTA INFERIOR LBS
Una cota inferior (lower bound) para la duración total del proyecto (makespan) es una aproximación al makespan la cual tiene la característica principal de ser siempre menor o igual al makespan óptimo.
La cota inferior es un parámetro importante por las siguientes dos razones:
- En primer lugar, si se tiene una cota inferior para el makespan, y durante el proceso de búsqueda se halla una solución cuyo makespan sea igual a dicha cota, esto significa que esta solución es óptima. Lo anterior se basa en lo siguiente:
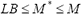
Siendo: LB = Cota Inferior (Lower Bound) M* = Makespan Óptimo M = Makespan de cualquier solución factible
Ahora,
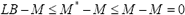
si M = LB, entonces:
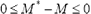
es decir
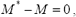
o sea
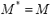
- En segundo lugar, una cota inferior para el makespan puede dar información acerca de la proximidad de una solución con respecto a la óptima así: Si se mide la proximidad a la solución óptima como porcentaje de su desviación,
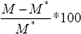
y si se asume que la cota inferior se encuentra lo suficientemente cercana a la solución óptima , una buena estimación para la proximidad sería:
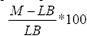
Esta estimación es útil, ya que para la gran mayoría de problemas no se conoce el valor del makespan óptimo.
En el presente trabajo la cota se usa con el objetivo de detener el algoritmo y evitar continuar la búsqueda, tal como se explicó anteriormente.
Existen numerosas cotas para el RCPSP [3]. En este trabajo se utiliza la de Stinson ya que es muy fácil de implementar y de buena calidad; aunque existen otras de mejor calidad (se acercan en promedio más al óptimo), pueden demandar más tiempo de procesamiento para su obtención.
La cota LBS, cota de Stinson, es una mejora de la denominada LB0 o cota de la ruta crítica que consiste en resolver el problema ignorando las restricciones de recursos.
Para hallar la LBS de cada problema, inicialmente se deben tomar cada una de las actividades que no pertenecen a la ruta crítica y calcular el intervalo de tiempo más largo en el cual es posible ejecutar cada actividad junto con las que pertenecen a la ruta crítica. La ejecución de cada actividad está sujeta al cumplimiento de las restricciones de precedencias y recursos impuestas en cada problema.
La cota de Stinson se obtiene de la siguiente manera:
Se obtiene(n) la(s) ruta(s) crítica(s). Se toman las actividades i que no pertenecen a la ruta crítica y se calcula para cada una de ellas su tiempo más próximo de inicio o early start (esi) y su tiempo más tardío de terminación o late finish (lfi). Se considera el intervalo (esi, lfi) para cada una de esas actividades y se determina la duración ei del intervalo continuo más largo contenido en (esi, lfi) durante el cual se puede ejecutar la actividad i total o parcialmente.
La cota de Stinson es LBS = LB0 + max(di – ei), donde di es la duración de la actividad i, y max(di – ei) significa lo que debe alargarse la ruta crítica para contener también la actividad que más tiempo requiere por recursos para su ejecución.
El cálculo para obtener la LBS es muy sencillo y usualmente da un valor mucho mejor que la cota de la ruta crítica (LB0).
6. ESTRATEGIA DE DURACIONES MÍNIMAS
En la implementación de los dos heurísticos, Enfriamiento Simulado y Búsqueda Tabú, se hace uso de la estrategia de Duraciones Mínimas, propuesta por los autores, concepto estrechamente ligado al uso de las cotas inferiores. El principal propósito del uso de las Duraciones Mínimas es reducir el tiempo de procesamiento del algoritmo descartando soluciones con un alto makespan.
La duración mínima DM(i) de una actividad i se determina de la siguiente manera:
En cualquier secuencia particular de actividades S, es necesario programar el inicio de cada una de ellas, de acuerdo a la posición en que se encuentre; así, cada actividad tiene un tiempo de inicio y un tiempo de terminación, donde este último es igual al tiempo de inicio más la duración de la actividad.
Siendo S una secuencia particular de actividades hallada por el algoritmo, se definen:
- Predecesor más tardío de la actividad i, PMT(i): predecesor de la actividad en la posición i, perteneciente a la secuencia S, con un mayor tiempo de terminación.
- TT(PMT(i)): tiempo de terminación de PMT(i).
- Mejor Makespan, MM: makespan de la mejor solución obtenida hasta el momento.
- Duración Mínima de la actividad i, DM(i): cota inferior LBS calculada para la subred conformada por la actividad de la posición i y cada uno de sus sucesores directos e indirectos.
Luego, si se tiene que:
![]()
Entonces se deduce que la secuencia S no posee un makespan menor al de la mejor solución obtenida hasta el momento; por lo tanto se puede descartar la secuencia S.
7. ENFRIAMIENTO SIMULADO (SA)
El funcionamiento del SA desarrollado en esta investigación, puede sintetizarse como se ilustra en la Figura 1 (Adaptado del algoritmo genérico del SA [11]).
Figura 1. Pseudos-código del algoritmo del SA para el RCPSP
Figure 1. SA algorithm pseudo code for the RCPSP.
Una solución o secuencia de actividades S, es una lista de actividades organizada de acuerdo con el orden en que se deben programar, es decir, cada actividad cuenta con un índice que indica su posición (o prioridad) dentro de la secuencia. Luego de programar cada una de las actividades de acuerdo con su índice o posición, se obtiene la duración total de la secuencia S o duración total del proyecto, llamado makespan.
En la presente investigación se realizan cuatro modificaciones al algoritmo genérico del SA descrito en [10], dos de las cuales son propuestas por los autores. Dichas modificaciones se presentan a continuación.
7.1 Criterio para la generación de cada secuencia de actividades Sa
Sa es una secuencia de actividades obtenida de la siguiente forma: se genera aleatoriamente una secuencia de actividades SP y se encuentra su ruta crítica, luego se generan todas la soluciones por medio del desplazamiento hacia adelante de las actividades de la(s) cadena(s) crítica(s) de SP. De todas las secuencias generadas, aquella con el menor makespan será escogida como la secuencia de interés Sa. Aunque esta estrategia se ha utilizado en otros heurísticos [12], los autores proponen su utilización en el SA en combinación con la estrategia explicada en 7.2. 7.2 Criterio para la generación de un determinado vecindario para cada secuencia de actividades Sa
Dada una solución o secuencia de actividades Sa, su vecindario se define como secuencia Sv que resulta de cambiar aleatoriamente dos actividades de Sa. De no ser posible intercambiar las dos actividades generadas por causa de las precedencias, se genera aleatoriamente un nuevo cambio hasta encontrar uno factible por precedencias.
Una vez encontrado un vecino factible, se calcula su makespan (Makespan(Sv)). Si este es menor que el actual, se acepta como la solución actual (incumbente). En caso contrario, si la solución es de menor calidad, se puede aceptar, aplicando el siguiente algoritmo:
- Se genera un número aleatorio a
- Se calcula = makespan(Sv) – makespan(Sa) (debe ser ? 0)
- Si a < , se acepta la solución, en caso contrario se rechaza.
La anterior función de probabilidad asigna mayor probabilidad de aceptación a las soluciones que se alejan menos de la actual.
7.3 Uso de la cota inferior lbs como criterio de parada
Cuando alguna secuencia de actividades S cumple la condición:
Makespan(S) = LBS,
entonces S es la solución óptima [13]. Esta propiedad fue explicada en el numeral 5 del presente trabajo.
7.4 Uso de las duraciones mínimas para reducir el tiempo de ejecución del algoritmo
En este algoritmo se aplica la Estrategia de Duraciones Mínimas, propuesta por los autores, cada que se va a programar una actividad, tal como se explica en el numeral 6 del presente trabajo.
7.5 Valor de los parámetros de entrada
Los valores asignados a cada parámetro son el resultado de un análisis y experimentación previos, con el fin de buscar, a criterio de los investigadores, valores apropiados.
- Temperatura máxima o inicial (Tmax). Este parámetro se halló según la metodología planteada en [14].
- Velocidad de enfriamiento (rT). La temperatura disminuye a una razón geométrica rT = 0.7 para todos los problemas. Este valor fue el mejor encontrado experimentalmente.
- Temperatura mínima (Tmin). Parámetro dado por la fórmula Tmin = (Tmax)*(rT (V –1)), siendo V el número de valores diferentes que tomará la Temperatura (T).
- Criterio de terminación del algoritmo. El algoritmo se detiene con base en el tiempo total de ejecución, para el cual se obtuvieron datos con diferentes valores entre 0.15 y 30.0 seg.
8. BÚSQUEDA TABÚ (TS)
El funcionamiento de TS desarrollado en esta investigación puede sintetizarse como se ilustra en la Figura 2.
Figura 2. Pseudos-código del algoritmo base de TS para el RCPSP
Figure 2. TS base algorithm pseudo-code for the RCPSP
A continuación se explican los criterios utilizados en cada uno de los cuatro pasos del algoritmo de TS.
8.1 Generación de una secuencia inicial de actividades: Sa
En la generación de la secuencia inicial de actividades se ha optado por la solución lexicográfica, la cual consiste en programar las actividades en el siguiente orden: actividad 1, actividad 2,..., actividad n.
La elección de esta secuencia como la inicial se debe fundamentalmente a dos razones: en primer lugar, a la facilidad y rapidez de programación, y en segundo lugar, a que en una exploración inicial, en la mayoría de las ocasiones, la solución lexicográfica resulta ser mejor en términos de calidad de la función objetivo que otras soluciones iniciales como la SPT, la LPT y soluciones aleatorias.
8.2 Generación de un vecindario
La generación de un vecindario (en el paso 2) para una solución Sb dada, se lleva a cabo mediante el desplazamiento hacia adelante de las actividades de la(s) cadena(s) críticas(s) de dicha secuencia, procediendo similarmente a como se explica en el numeral 7.1.
8.3 Uso de la cota inferior lbs como criterio de parada
Cuando alguna secuencia de actividades S cumple la condición:
Makespan(S) = LBS,
entonces S es la solución óptima [13]. Esta propiedad fue explicada en el numeral 5 del presente trabajo.
8.4 Uso de las duraciones mínimas para reducir el tiempo de ejecución del algoritmo
Para la implementación de la estrategia de Duraciones Mínimas, propuesta por los autores, en el algoritmo de Búsqueda Tabú es necesario modificar la forma de aplicar esta estrategia.
Dado que la solución generada por el criterio de aspiración es generalmente de muy mala calidad, se decidió aplicar la Estrategia de Duraciones Mínimas luego de pasadas 20 iteraciones después de una aspiración, con el fin de permitirle al algoritmo intensificar la búsqueda.
8.5 Criterio de aspiración
Como criterio de aspiración se consideran dos posibilidades, así:
- Cuando se tiene una solución factible que está presente en el vecindario de una solución actual y también en la lista tabú. En este caso, si la calidad de la solución hallada es superior a la calidad de la mejor solución encontrada hasta el momento, se permite violar el estatus tabú para aceptar dicha solución.
- Cuando el algoritmo lleva un determinado número de iteraciones sin mejorar la calidad de la solución. En este caso se podría considerar que el vecindario se encuentra en una región cercana a un óptimo local; por lo tanto, se debe optar por la búsqueda en otras regiones (regiones no visitadas).
Para iniciar la búsqueda en nuevas regiones (regiones no visitadas) se utiliza un indicador de la frecuencia con que una actividad es programada en una posición dada de la secuencia. Así cuando se procede a escoger la posición que debe ocupar cada actividad se procura seleccionar las posiciones de menor frecuencia. Para ello los autores utilizan una matriz cuadrada que indica las frecuencias de cada actividad (filas) en cada posición (columnas).
Para esta investigación, luego de varias pruebas, se ha determinado que 30 iteraciones sin mejorar es un buen criterio de aspiración.
8.6 Valor de los parámetros de entrada
- Tamaño de la Lista Tabú. Su tamaño se considera igual al número de actividades del problema. Cuando la Lista Tabú se encuentra llena, los nuevos registros hacen que los últimos sean eliminados.
- Criterio de terminación del algoritmo. Similar a SA.
9. EVALUACIÓN Y ANÁLISIS DE RESULTADOS
Para la evaluación de los dos programas desarrollados, SA y TS, se utilizaron 960 problemas (480 problemas de 30 actividades y cuatro recursos, y 480 problemas de 60 actividades y cuatro recursos) obtenidos de la librería PSPLIB (Librería de problemas benchmark del tipo RCPSP, usada por gran cantidad de investigadores europeos en el tema (http://www.bwl.uni-kiel.de/Prod/psplib/) creada por Kolisch, R. y A. Sprecher). Para los problemas de 30 actividades se cuenta con el valor del makespan óptimo y para los problemas de 60 actividades se tienen las mejores soluciones obtenidas hasta el momento por diferentes investigadores (de las cuales no se puede garantizar que sean la solución óptima, ya que para algunos problemas aún no se conoce), obtenidas igualmente de la librería PSPSLIB.
Los algoritmos fueron desarrollados en el lenguaje Visual Basic, versión 6.0.
9.1 Resultados del Enfriamiento Simulado
Para la evaluación de esta heurística se ejecutó el programa de SA desarrollado mediante el algoritmo de la Figura 1 para diferentes valores del criterio de parada: tiempo de ejecución. El programa se corrió en primer lugar para los 480 problemas de 30 actividades con y sin la estrategia de Duraciones Mínimas. Los resultados obtenidos se ilustran en la Tabla 1.
Tabla 1. Resultados SA – 30 actividades, con y sin Duraciones Mínimas
Table 1. SA results – 30 jobs, with and without minimal duration
Tiempo: Tiempo promedio de ejecución de los 480 problemas.
Desviación: Desviación promedio de la mejor solución hallada por el algoritmo respecto a la solución óptima de cada uno de los 480 problemas.
En la Tabla 1 se puede observar como la estrategia que utiliza Duraciones Mínimas es superior a la estrategia que no lo hace. Nótese que en todas las entradas de la Tabla (excepto en la segunda), la estrategia con Duraciones Mínimas arroja siempre un menor tiempo de ejecución y una menor desviación.
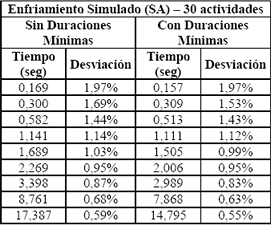
Posteriormente el programa de SA se corrió para los 480 problemas de 60 actividades con y sin la estrategia de Duraciones Mínimas. Los resultados obtenidos se ilustran en la Tabla 2.
Tabla 2. Resultados SA – 60 actividades, con y sin Duraciones Mínimas
Table 2. SA results- 60 jobs, with and without minimal duration
Tiempo: Tiempo promedio de ejecución de los 480 problemas.
Desviación: Desviación promedio de la mejor solución hallada por el algoritmo respecto a la mejor solución conocida de cada uno de los 480 problemas.
Al observar los datos de la Tabla 2, se concluye que no existe superioridad absoluta de una estrategia sobre la otra. Sin embargo, en las primeras siete filas de la Tabla 2, la estrategia sin Duraciones Mínimas arroja siempre un menor tiempo de ejecución y una menor desviación (es decir, existe superioridad por parte de esta estrategia en esa sección de la Tabla). A partir de la fila número ocho, aunque la estrategia sin Duraciones Mínimas arroja una menor desviación, la estrategia con Duraciones Mínimas arroja un menor tiempo de ejecución.
Este último caso puede ser ocasionado porque en la estrategia con Duraciones Mínimas siempre se considera el tiempo requerido para calcular las Duraciones Mínimas de cada subred en cada problema, DM(i). Este tiempo afecta menos el tiempo total de ejecución a medida que el algoritmo realiza más iteraciones; es decir, la estrategia de Duraciones Mínimas es más útil en la medida en que sea mas alto el tiempo de parada del algoritmo, o lo que es equivalente, a mayor número de iteraciones realizadas.
9.2 Resultados de la Búsqueda Tabú
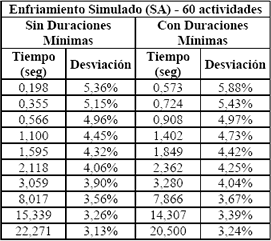
Para la evaluación de esta heurística se ejecutó el programa de TS desarrollado mediante el algoritmo de la Figura 2 para diferentes valores del criterio de parada: número de iteraciones. El programa se corrió en primer lugar para los 480 problemas de 30 actividades con y sin la estrategia de Duraciones Mínimas. Los resultados obtenidos se muestran en la Tabla 3.
Tabla 3. Resultados TS – 30 actividades, con y sin Duraciones Mínimas
Table 3. TS results- 30 jobs, with and without minimal duration
Tiempo: Tiempo promedio de ejecución de los 480 problemas.
Desviación: Desviación promedio de la mejor solución hallada por el algoritmo respecto a la solución óptima de cada uno de los 480 problemas.
De la Tabla 3 se puede observar cómo, al contrario de lo sucedido con SA, la estrategia de Duraciones Mínimas no entrega resultados muy alentadores. Posteriormente el programa de TS se corrió para los 480 problemas de 60 actividades con y sin la estrategia de Duraciones Mínimas. Los resultados obtenidos se ilustran en la Tabla 4.
Tabla 4. Resultados TS – 60 actividades, con y sin Duraciones Mínimas
Table 4. TS results- 60 jobs, with and without minimal duration
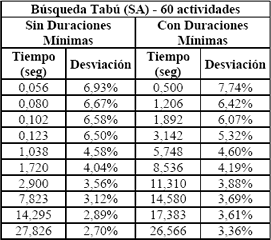
Tiempo: Tiempo promedio de ejecución de los 480 problemas.
Desviación: Desviación promedio de la mejor solución hallada por el algoritmo respecto a la mejor solución conocida de cada uno de los 480 problemas.
Al observar los datos de la Tabla 4, nuevamente se nota una superioridad del algoritmo clásico sobre el que implementa la estrategia de las Duraciones Mínimas
9.3 Comparación de los métodos, SA – TS
Para comparar los dos métodos utilizados en esta investigación, SA y TS, se escogió entre las dos alternativas, con o sin Duraciones Mínimas, la que arrojó mejores resultados tal como se muestra en la Tabla 5.
Tabla 5. Alternativa Seleccionada
Table 5. Selected Alternative

SDM: Estrategia sin duraciones mínimas.
CDM: Estrategia con duraciones mínimas.
De esta manera, para los problemas de 30 actividades, según lo analizado en el numeral 9.1, la estrategia con Duraciones Mínimas produce mejores resultados sólo para la técnica de SA.
Para los problemas de 60 actividades, se concluye que para tiempos de procesamiento bajos se consiguen mejores resultados sin la estrategia de Duraciones Mínimas, tanto para el método de SA como para el de TS.
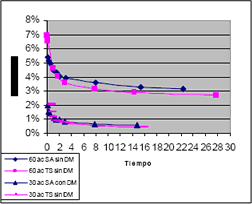
Con base en lo anterior se construye el gráfico de la Figura 3. En esta figura puede observarse como para problemas de 30 actividades tanto TS como SA con Duraciones Mínimas arrojan resultados muy similares, mientras que para problemas de 60 actividades se nota la superioridad de TS para tiempos superiores a aproximadamente 1.0 seg.
Figura 3. Comparación SA – TS con los mejores resultados obtenidos para cada algoritmo
Figure 3. SA – TS comparison with the best results obtained for each algorithm
Por otro lado no se debe olvidar la posibilidad de que los resultados mejoren con las estrategias de Duraciones Mínimas para tiempos mayores, ya que el cálculo de las duraciones mínimas se realiza una vez y por lo tanto puede interpretarse como un tiempo fijo (por similitud con el problema de costo fijo) que es absorbido en menores cantidades en la medida en que el tiempo variable (número de iteraciones por similitud nuevamente con el problema de costo fijo) sea mayor.
10. TRABAJO FUTURO
Con el fin de hacer comparaciones con otros autores de talla internacional, se utilizará como criterio de parada el Número Máximo de Schedules [15]. Este criterio tiene la ventaja de que no depende ni del lenguaje de programación ni del procesador utilizado. El inconveniente que se podría presentar es que no todos los heurísticos permiten calcular el número de schedules (aunque no es nuestro caso) y que en algunos casos los tiempos requeridos para calcular un Schedule podrían variar considerablemente.
Actualmente se está trabajando en el desarrollo de una nueva estrategia basada en un indicador del nivel de complejidad de cada problema particular, el cual ha presentado algunos resultados preliminares prometedores.
Esta estrategia consiste en variar algunos parámetros de los algoritmos, tales como el criterio de parada, según la complejidad del problema. De esta forma a los problemas que presentan mayor complejidad se les permitirá tomar mayor esfuerzo en su solución.
Adicionalmente se desarrollarán algoritmos para resolver el RCPSP utilizando los métodos Grasp y Algoritmos Genéticos.
REFERENCIAS
[1] BELL C. E., PARK K., Solving Resource-Constrained Project Scheduling Problems by A* Search. Naval Research Logistics, Vol. 37, pp. 61-84, 1990. [ Links ]
[2] DEMEULEMEESTER E., HERROELEN W., A Branch and Bound Procedure for the Multiple Resource-Constrained Project Scheduling Problem, Management Science, 38, pp. 1803-1818, 1992. [ Links ]
[3] MINGOZZI A., MANIEZZO V., RICCIARDELLI S., and BIANCO L., An exact algorithm for the Resource Constrained Project Scheduling Problem Based on a New Mathematical Formulation, Technical Report, No. 32, 1994. [ Links ]
[4] BLAZEWICZ, J.; LENSTRA, J. K. and RINNOOY KAN A. H. G. Scheduling Projects Subject to Resource Constraints: Classification and Complexity. Discrete Applied Mathematics, 5, 11-24, 1983. [ Links ]
[5] METRÓPOLIS, N; ROSENBLUTH, A.; TELLER, A. and TELLER, E. Equations of state calculations by fast computing machines. The journal of chemical physics, Vol. 21, No. 6. 1953. [ Links ]
[6] KIRKPATRICK, S.; GELATT, C. D. and VECCHI, M. P. Optimization by Simulated Annealing. Science 220, pp. 671-680. 1983. [ Links ]
[7] GUTIÉRREZ, M. Á.; DE LOS COBOS, S. G. y PÉREZ Salvador, B. R. Optimización con recocido simulado para el problema de conjunto independiente. Revista En Línea. Universidad Autónoma Metropolitana. México, 1998. En línea: http://www.azc.uam.mx/publicaciones/enlinea2/3-2.html. (Consulta: Octubre 13 de 2004). [ Links ]
[8] VAN HOREBEEK, Johan. Probabilidad y estadística aplicada. 1998. En línea: http://www.cimat.mx/~horebeek/cursus/node40.html. (Consulta: 18 de noviembre de 2003). [ Links ]
[9] GLOVER, F. Tabu Search, Part I. ORSA Journal on Computing, pp. 190-206. 1989. [ Links ]
[10] DÍAZ, A; GLOVER, F; GHAZIRI, H.; GONZÁLEZ, J.; LAGUNA, M.; MOSCATO, P. y TSENG, F. Optimización Heurística y Redes Neuronales. Editorial Paraninfo, pp. 105-142. 1996. [ Links ]
[11] FOGEL, David. How to solve it: Modern Heuristics. Ed Springer, 2000. [ Links ]
[12] RANGASWAMY, B.; SINGH, Jain A.; GLOVER, F. Tabu Search Candidate List Strategies in Scheduling. 1998. [ Links ]
[13] STINSON, J. P.; Davis E. W.; KHUMAWALA, B. M. Multiple Resource-Constrained Scheduling Using Branch and Bound, AIIE Transactions, 1978. [ Links ]
[14] CHO J-H, KIM Y-D, A simulated Annealing for RCPSP, Journal of the Operation Research Society, 48, 736-744, 1997. [ Links ]
[15] KOLISCH, R. and HARTMANN, S. Experimental Investigation of Heuristics for Resource-Constrained Project Scheduling: An Update. Technical University of Munich. OR Consulting. Germany, 2004. [ Links ]