Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
DYNA
versão impressa ISSN 0012-7353versão On-line ISSN 2346-2183
Dyna rev.fac.nac.minas v.74 n.152 Medellín maio/ago. 2007
EFECTO DE LA ALTITUD EN EL ANÁLISIS TERMOECONÓMICO DE UN SISTEMA DE COGENERACIÓN
THE EFFECT OF ALTITUDE ON THE THERMOECONOMIC ANALYSIS OF A COGENERATION SYSTEM
ANDRÉS AGUDELO SANTAMARÍA
Grupo GIMEL. Universidad de Antioquia, afagudel@udea.edu.co
JOHN AGUDELO SANTAMARÍA
Grupo GIMEL. Universidad de Antioquia, jragude@udea.edu.co
CARLOS SÁNCHEZ LÓPEZ
Grupo de Combustibles Alternativos. Universidad Nacional, Sede Medellín, casanchez@unalmed.edu.co
Recibido para revisar 19 de Mayo de 2006, aceptado 26 de Septiembre de 2006, versión final 26 de Octubre de 2006
RESUMEN: Se estima el efecto de la altitud sobre el diagnóstico termoeconómico de un sistema de cogeneración con turbina de gas. Para aislar este efecto se mantuvo constante la relación másica aire-combustible en la cámara de combustión. La variación de las condiciones del ambiente con la altitud se realizó por medio de un modelo hidrostático, considerando el aire como gas ideal y asumiendo variación lineal de la temperatura. Las condiciones del estado muerto se tomaron tanto constantes como variables para efectos de comparación. Al incrementar la altitud disminuye la densidad del aire, causando una caída de potencia en el sistema de aproximadamente 20%. Se encontró que ésta es la principal causa de disminución de la tasa de costo asociada al producto total. El costo exergético unitario del producto del sistema se incrementa cerca de 3% a 3000 metros sobre el nivel del mar (msnm), lo que significa que a mayor altitud cuesta más producir cada unidad de potencia.
PALABRAS CLAVE: Efecto altitud, Análisis termoeconómico, Análisis exergético, Cogeneración, Problema CGAM, Turbinas de gas.
ABSTRACT: In this work the altitude effect on the thermoeconomic diagnosis of a gas turbine cogeneration system has been determined. In order to isolate this effect, the air-fuel ratio was fixed in the combustion chamber. The variation of environmental conditions with altitude was done by means of a hydrostatic model, taking air as an ideal gas and assuming linear temperature variation. For comparison purposes dead state conditions were taken both constant and variable. Air density decreases for increasing altitude, causing a power drop in the system of about 20%. It was found that this is the main reason for the total product cost rate decreasing. The total product cost per exergy unit increase up to 3% for 3000 m above sea level, which means that it is more expensive to produce every power unit as altitude increases.
KEYWORDS: Altitude effect, Thermoeconomic analysis, Exergy analysis, Cogeneration, CGAM problem, Gas turbines.
1. INTRODUCCIÓN
En este trabajo se analiza un sistema de cogeneración con turbina de gas denominado CGAM (por las iniciales de sus autores: C. Frangopoulos; G. Tsatsaronis; A. Valero y M. Von Spakovsky), usado en la década de 1990, para comparar las diferentes metodologías de análisis termoeconómico [1, 2].
Los trabajos relacionados con este problema, y en general lo hecho en el campo del análisis termoeconómico, consideran las condiciones estándar como ambiente de referencia para el análisis [1, 2, 3, 4, 5, 6]. Sin embargo, en gran parte de Latinoamérica, especialmente en Colombia, se tienen importantes centros urbanos a grandes alturas sobre el nivel del mar. Está ampliamente demostrado que las condiciones atmosféricas afectan de forma sensible el funcionamiento de los sistemas energéticos ya que la potencia de quemadores atmosféricos, turbinas de gas y motores de combustión interna de aspiración natural disminuye proporcionalmente con la altitud [7, 8, 9], lo que justifica una evaluación del efecto de ésta sobre el análisis termoeconómico y determinar si se necesita tener en cuenta las condiciones locales.
En la figura 1 se presenta un esquema de la planta de cogeneración a analizar. El compresor se denota con C, la turbina con T, la cámara de combustión con CC, el precalentador con PC y el evaporador con EV. En la cámara de combustión se inyecta gas natural a 12 bar y 25 °C. La turbina en condiciones de referencia entrega 30 MW de potencia útil. En el estado 8 entra agua a 25 °C y 20 bar y en 9 sale vapor saturado seco a la misma presión. El coeficiente de exceso de aire es tomado de Tsatsaronis y Moran [3] con un valor de 3.5.
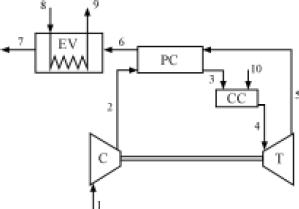
Figura 1. Esquema del problema CGAM
Figure 1. CGAM problem sketch
2. ANÁLISIS TERMODINÁMICO
Por medio de la aplicación de balances de masa y energía se determinan las propiedades termodinámicas en los diferentes puntos del sistema partiendo de la información inicial. En este análisis se han considerado adiabáticos todos los componentes excepto la cámara de combustión, en la que se pierde por transferencia de calor alrededor del 2% de la energía suministrada por el combustible [1, 5]. Se ha tomado una eficiencia isentrópica constante de 0.86 para el compresor y la turbina, lo cual concuerda con el hecho que menciona Jubeh [10] de que la altitud no afecta la eficiencia de segunda ley de una planta con regeneración como la estudiada. La razón de la presión de salida de la turbina a la atmosférica se mantiene constante con la altitud, al igual que la temperatura de los gases a la salida del evaporador. Esto último con el fin de evitar condensación del vapor de agua en los conductos de escape. Adicionalmente se considera combustión completa para determinar la composición de los gases en el punto 4 y con el fin de aislar el efecto de la altitud, se conserva constante la relación másica aire-combustible controlando el flujo másico de combustible.
2.1 Efecto de la altitudLas condiciones atmosféricas afectan los sistemas de combustión, ya que de ellas dependen las condiciones del aire empleado como comburente. Al aumentar la altitud disminuyen la presión, la temperatura atmosférica y la densidad del aire. Como lo muestran Lapuerta et al. [9], la concentración de oxígeno en el aire también decrece con la altitud, pero hasta 3000 msnm su disminución no es significativa. De otro lado los autores han realizado un análisis exploratorio, encontrando que el efecto de la humedad relativa es prácticamente insignificante, por lo que se omite para análisis posteriores.
El análisis ha sido realizado en estado estacionario, considerando los gases como ideales. El efecto de la altitud se introduce mediante un modelo hidrostático de la presión atmosférica. La variación de la temperatura con la altitud ha sido tomada del modelo atmosférico de la NASA [11]. La presión a nivel del mar es 101.325 kPa y la temperatura de 298.15 K. La presión y la temperatura del estado muerto se hacen iguales a la atmosférica. Estas últimas condiciones modifican el valor determinado para las exergías químicas, las cuales deben tener una corrección por presión y por temperatura, ya que los valores calculados corresponden a condiciones estándar. Según McGovern [12], sin embargo, el cambio de la exergía química para variaciones moderadas en estas propiedades se puede despreciar sin sacrificar la precisión de los cálculos.
En la figura 2 se observa que tanto la presión como la temperatura atmosféricas disminuyen con la altitud respecto al nivel de mar, siendo más marcado el cambio en la presión. Este comportamiento explica la disminución en la densidad del aire observado con la altitud. Sin embargo, a pesar de que disminuya la densidad del aire, la velocidad del compresor y la turbina se mantienen constantes, por lo que es válido asumir caudal de aire constante en el compresor.
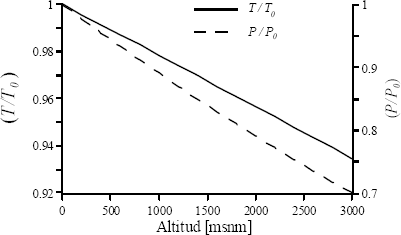
Figura 2. Variación de T0 y P0 con la altitud
Figure 2. Variation of T0 y P0 with altitude
La composición del aire atmosférico empleada en el análisis corresponde a una humedad relativa de 60% (76.91 % N2, 20.457% O2, 0.029% CO2 y 2.514% H2O). Las propiedades termodinámicas de los gases se calculan según los modelos propuestos por Wagner et al. [13] y aquellas para el agua según la formulación IAPWS 97 [14].
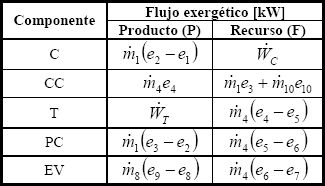
En la metodología termoeconómica se emplea el análisis exergético para determinar los flujos exergéticos asociados al recurso y al producto de cada componente, así como las tasas de destrucción y pérdida de exergía en éstos. En la tabla 1 se presentan los términos del análisis exergético para el sistema de cogeneración de interés.
Tabla 1. Términos del análisis exergético
Table 1. Exergy analysis terms
En cada caso la exergía específica se calcula como la suma de los aportes físico y químico, despreciando las energías cinética y potencial, tal como se ilustra en la ecuación (1):
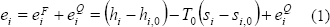
Como es comentado por Moran y Sciubba [15], los productos de combustión están compuestos de sustancias presentes en el ambiente, de modo que su exergía química depende sólo de las diferencias de concentración de cada especie con éste.
En el análisis del problema CGAM se suele emplear metano como combustible. En este trabajo se ha utilizado gas natural de la Guajira, el cual es una mezcla gaseosa que se considera ideal con la composición mostrada en la tabla 2.
Tabla 2. Composición del combustible. Según: Amell et al. [16]
Table 2. Fuel composition. By: Amell et al. [16]

La exergía química del combustible utilizada ha sido obtenida según Kotas [17] y usando la composición de la tabla 2 se llega a que su valor es 50050.7 kJ/kg, magnitud ligeramente mayor a su poder calorífico inferior (48773.3 kJ/kg).
Para el análisis económico se requiere conocer además los flujos nergético de los puntos 2, 3, 9 y 10, así como las tasas de pérdida de exergía al medio. Para calcular el flujo nergético asociado al calor perdido en la cámara de combustión, se asume que el aislamiento térmico garantiza una temperatura superficial de 80 ºC, con lo cual el flujo energético de pérdida en la cámara de combustión se calcula como se ilustra en (2).
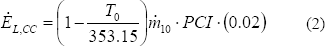
Donde PCI es el poder calorífico inferior del combustible. La tasa de pérdida de exergía en el evaporador es la correspondiente en el punto 7. En los demás componentes no se pierde exergía al medio. La tasa de destrucción de exergía en cada componente se determina fácilmente a partir de su balance exergético.
La eficiencia exergética de cada componente se define como:

3. ANÁLISIS ECONÓMICO
Se necesita determinar las tasas de costo asociadas con el producto de cada componente del sistema. Éstas comprenden los costos económicos, es decir, aquellos asociados con la inversión en la compra de los equipos, los impuestos, la operación y el mantenimiento, entre otros. La tasas de costo también comprenden los costos nergéticos o termodinámicos que incluyen el efecto de las pérdidas o degradaciones de energía.
De acuerdo a Bejan et al. [18] La tasa de costo asociada con el producto de un componente del sistema se define como:

Donde P se refiere al producto, F al recurso y el segundo término de la derecha es la tasa de costos no termodinámicos, principalmente los de inversión de capital, de operación y mantenimiento, el cual se puede aproximar para cada componente [18]:
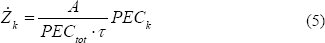
En la ecuación (5) el término A es una constante asociada con los cargos impositivos y los costos de operación y mantenimiento anuales. El término PECk se refiere al costo de compra de cada componente, t es el tiempo de operación anual de la planta. El término en el denominador está dado por la expresión (6):

Los costos de compra de cada componente se han obtenido de los valores reportados por Bejan et al. [18]. Se ha tomado un tiempo de funcionamiento de 24 horas diarias, todos los días del mes durante 10 meses al año. Las tasas de costo asociadas con el producto y el recurso del k-ésimo componente se calculan según (7):

Donde G puede ser P o F. El primer término del segundo miembro es el costo exergético unitario. Los flujos exergéticos en esta expresión proceden del análisis termodinámico.
Finalmente, se calculan algunas variables termoeconómicas importantes para diagnosticar el sistema [2, 18].En primer lugar, se calcula la diferencia de costos relativa de cada componente según la ecuación (8).
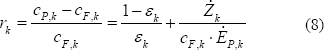
Este parámetro expresa el incremento relativo en el costo unitario promedio entre el producto y el recurso de un componente, por lo que su variación es más representativa que aquella del costo del producto. Otro parámetro importante es el factor exergoeconómico (fk), el cual expresa la contribución relativa de los costos no exergéticos:
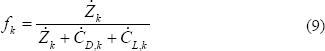
Los costos de las tasas de destrucción y pérdida de exergía se definen según las ecuaciones (10) y (11); en donde se asume que la pérdida o destrucción de exergía se cubre con una entrada adicional de combustible o recurso a cada componente.

3.1 Balance de costos
De forma general, el balance de costos de un componente se expresa como [18]:
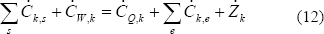
Esta ecuación establece que el costo total de las corrientes exergéticas de salida es igual al gasto total hecho para obtenerlas. En la expresión anterior el subíndice e se refiere a las corrientes de entrada y s a las de salida. W se refiere al trabajo que sale del componente y Q al calor que entra. Aplicando este balance a todos los componentes se obtiene igual número de ecuaciones. Dado que el número de incógnitas supera al de ecuaciones se necesitan relaciones adicionales entre los diferentes costos exergéticos. Para esto se usa la teoría contable, la cual establece que el costo unitario de una corriente solo cambia si se le añade exergía a ésta durante el proceso en un componente [18].
Por tanto, para aquellas corrientes que disminuyen o no cambian su exergía al paso por los componentes se considera que su costo unitario o exergético permanece constante. Adicionalmente, el costo exergético del trabajo producido por la turbina es igual al empleado en el compresor. El costo exergético del combustible, c10, se calcula usando valores actuales de la UPME [19] para el gas natural en Colombia y para el valor del dólar.
3.2 Costo total del producto del sistema
Al resolver las ecuaciones resultantes de los balances de costos se determinan los costos exergéticos de interés, con lo cual, se puede determinar el costo total del producto según la ecuación (13):

En un proceso de optimización termoeconómica, ésta sería la función objetivo a minimizar. En este caso, que se tienen dos productos: potencia eléctrica y vapor, el denominador en la expresión (13) debe ser la suma de los flujos exergéticos del producto del evaporador y del trabajo útil obtenido en la turbina.
4. RESULTADOS Y DISCUSIÓN
En las tablas 3 y 4 se presentan los resultados obtenidos a nivel de mar para el sistema de cogeneración.
Tabla 3. Resultados generales
Table 3. General results

Tabla 4. Resultados para los componentes
Table 4. Component results
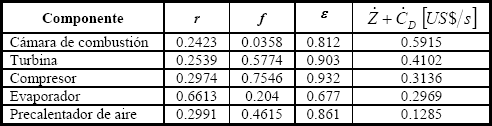
Los resultados anteriores corresponden a un flujo másico de aire a nivel de mar de 116.3 kg/s, el cual permite obtener el trabajo útil deseado para las eficiencias isentrópicas fijadas para el compresor y la turbina, así como la relación aire/combustible especificada. Para las condiciones de funcionamiento empleadas se obtiene una tasa de costo total alta, lo que significa que éstas están alejadas del óptimo termoeconómico, en el cual la tasa de costo total es menor a 1 US$/s [1]. Esto no altera el efecto de la altitud sobre la respuesta del sistema, ya que los resultados son relativos a los correspondientes a nivel de mar. El costo exergético unitario del producto del sistema permite valorar con una base racional las corrientes útiles del mismo.
En la tabla 4 los componentes están ordenados según su importancia de costos (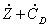 ). Los esfuerzos de mejora del sistema se deben concentrar en los componentes con alto valor de este parámetro. El evaporador presenta la mayor diferencia de costos relativa y la menor eficiencia exergética. Incrementar su eficiencia, aún a costa de elevar su costo de inversión puede conducir a disminuir la tasa de costo total del sistema. De otro lado, es claro que la mayoría de los costos asociados con la cámara de combustión se deben a destrucción de exergía, como lo indica su bajo factor exergoeconómico. Entre tanto, el compresor y la turbina tienen los factores exergoeconómicos más altos debido a sus elevados precios de compra.
). Los esfuerzos de mejora del sistema se deben concentrar en los componentes con alto valor de este parámetro. El evaporador presenta la mayor diferencia de costos relativa y la menor eficiencia exergética. Incrementar su eficiencia, aún a costa de elevar su costo de inversión puede conducir a disminuir la tasa de costo total del sistema. De otro lado, es claro que la mayoría de los costos asociados con la cámara de combustión se deben a destrucción de exergía, como lo indica su bajo factor exergoeconómico. Entre tanto, el compresor y la turbina tienen los factores exergoeconómicos más altos debido a sus elevados precios de compra.
Tradicionalmente se ha empleado un ambiente de referencia a 298.15 K y 101.325 kPa como estado muerto para determinar la exergía física. La figura 2 muestra que la presión y temperatura del ambiente disminuyen con la altitud, aumentado la capacidad de realizar trabajo de las corrientes a alta presión y temperatura, y afectando los resultados del análisis energético como lo muestra también Jubeh [10]. Por lo tanto, buscando exactitud, en este trabajo se han variado P0 y T0 con la altitud. En la figura 3 se presenta la variación del costo exergético unitario total con la altitud. Para efectos comparativos se incluye el correspondiente a un estado muerto fijo.
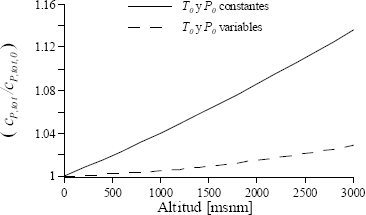
Figura 3. Variación del costo exergético unitario total
Figure 3. Variation of total cost per unit exergy
Al aumentar la altitud también lo hace el costo unitario del sistema, alcanzando un incremento de cerca de 3% a los 3000 msnm. El incremento es mucho más marcado para el caso de condiciones de estado muerto constantes, pero esto es menos representativo de lo que sucede en realidad. El incremento observado tiene implicaciones importantes en la viabilidad económica de la planta estudiada, ya que el pequeño porcentaje se puede traducir en mucho dinero, dependiendo de la producción requerida por el sistema. En contraste con lo anterior, la figura 4 muestra una importante disminución de la tasa de costo total del sistema con la altitud, es decir que a mayor altitud se requiere menos flujo de dinero para operar la planta. Este resultado no contradice el anterior, pues la tasa de costo del sistema depende tanto del costo unitario como del flujo exergético producido por el mismo, el cual disminuye marcadamente (ver figura 5).
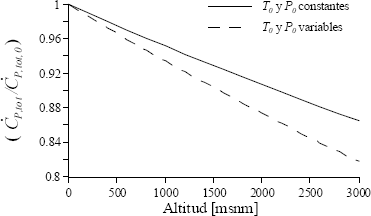
Figura 4. Variación de la tasa de costo total
Figure 4. Total cost rate variation
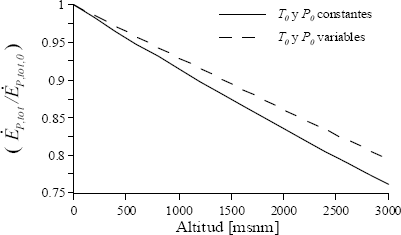
Figura 5. Variación del producto del sistema
Figure 5. System product variation
La marcada disminución en el producto del sistema mostrada en la figura 5 explica el comportamiento de la tasa de costo total del sistema. Aunque el costo unitario aumenta (se hace más caro producir una unidad de exergía), se obtiene mucho menos producto por unidad de tiempo, haciendo que disminuya el costo total por unidad de tiempo.
Nuevamente, el considerar un estado muerto fijo conduce a diferencias importantes en los resultados. La disminución observada en esta figura se debe a que los productos del sistema, electricidad (trabajo útil) y vapor, disminuyen a medida que aumenta la altitud (ver figura 6). En el caso del trabajo útil, la curva corresponde a la caída de potencia típica de una turbina con la altitud (derating), causando a su vez que el potencial de cogeneración de los gases disminuya, por lo que la producción de vapor se comporta también de forma decreciente con la altitud.
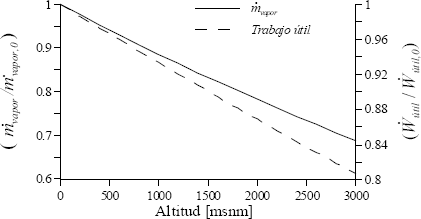
Figura 6. Variación del vapor y el trabajo producidos por el sistema
Figure 6. Variation of steam and work produced by the system
Al disminuir la densidad del aire con la altitud también lo hace el flujo másico de las corrientes en todos los componentes, lo cual se traduce en menos potencia para generar trabajo y vapor. Adicionalmente, con la altitud también disminuye la temperatura de los gases que entran al generador de vapor, lo cual sumado a que la temperatura de éstos a la salida se mantiene por encima de 400 K, contribuye a disminuir el flujo de vapor producido. El comportamiento del trabajo útil del sistema es característico de la pérdida de potencia de la turbinas con la altitud [7].
La diferencia de costos relativa del evaporador disminuye con la altitud, lo cual favorece el costo unitario del vapor producido, pero la del compresor y la turbina se incrementan significativamente, contribuyendo a que el costo unitario del trabajo producido también lo haga. El efecto neto, como se expuso previamente, es un aumento del costo unitario del sistema.
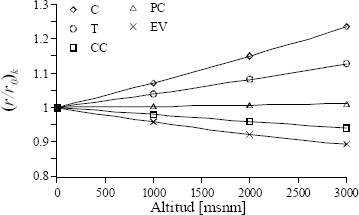
Figura 7. Variación de la diferencia de costos relativa de los componentes
Figure 7. Variation of the components' relative cost difference
El factor exergoeconómico de todos los componentes aumenta con la altitud (ver figura 8), lo que indica que se hacen menos importantes los costos relativos a la destrucción y pérdida de exergía. El aumento más marcado lo presenta la cámara de combustión, que es el componente donde más aportan los costos termodinámicos. De igual modo, se observa un aumento considerable para el evaporador. Estos aumentos se deben más a la disminución de las pérdidas exergéticas al medio que a la destrucción de exergía, como lo comprueba la poca variación de las eficiencias exergéticas de los componentes (figura 9).
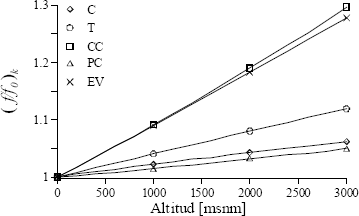
Figura 8. Variación del factor exergoeconómico de los componentes
Figure 8. Variation of the exergoeconomic factor of the components
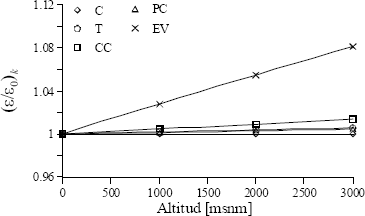
Figura 9. Variación de la eficiencia exergética de los componentes
Figure 9. Variation of components exergy efficiency
Como era de esperarse, la eficiencia del compresor y la turbina se mantiene prácticamente constante con la altitud [7, 10]. El aumento observado en la eficiencia del evaporador se debe a la definición de ésta. El término del recurso, que se encuentra en el denominador, disminuye más rápido con la altitud que el término del producto, debido al efecto combinado de la disminución del flujo másico y de la diferencia de temperaturas entre entrada y salida de los gases a causa de fijar T7.
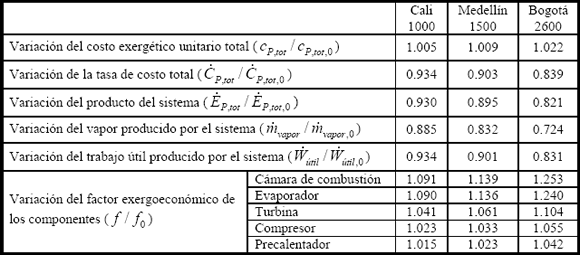
Para las principales ciudades colombianas que se encuentran a grandes altitudes tales como Cali, Medellín y Bogotá en promedio a 1000, 1500 y 2600 msnm respectivamente, se tienen los siguientes resultados:
Dado que al tomar las condiciones del estado muerto como variables se obtienen resultados más reales, en la tabla 5 solo se muestran los resultados de las principales variables termoeconómicas para este caso. Las centrales de generación que existen en Colombia, operando en ciclo abierto o ciclo simple para el sistema interconectado nacional, no tienen aprovechamiento de cogeneración; por tanto el costo exergético es mayor bajo estas condiciones.
Tabla 5. Análisis termoeconómico para ciudades colombianas – condiciones de estado muerto variables
Table 5. Thermoeconmic analysis for colombian cities – variable dead state conditions
De otro lado este análisis no ha incluido los costos relacionados con el transporte de gas natural, factor importante para el caso nacional, donde los precios entre la región atlántica y la zona centro del país pueden aumentar hasta en un 200% por el costo asociado con el transporte, según documentos de planeación de la expansión de la UPME para el año 2007 [20]. Este costo no termodinámico, de haberse incluido en el estudio realizado, arrojaría un mayor crecimiento del factor exergoeconómico que el reportado en la figura 8, porque, en la mayoría de casos, las ciudades ubicadas a gran altitud están también alejadas de los principales pozos de gas colombianos.
5. CONCLUSIONES
- El efecto de la altitud sobre las prestaciones de un sistema térmico es considerable y afecta igualmente las variables termoeconómicas principales, por lo que en los análisis es necesario usar las condiciones atmosféricas locales de los sitios que se encuentren a grandes alturas sobre el nivel del mar.
- Se recomienda igualar las condiciones del estado muerto a las atmosféricas de cada sitio, ya que de este modo se valora con exactitud el potencial de cada fuente energética y se obtienen resultados más confiables.
- La tasa de costo del producto total del sistema disminuye de forma proporcional al incremento en la altitud, debido a la consiguiente disminución de la potencia producida por el sistema.
- El costo exergético unitario total se ve incrementado ligeramente con la altitud, hecho que afecta el rendimiento económico del sistema y se debe tener en cuenta al evaluar proyectos de inversión en plantas térmicas a grandes alturas.
- En general, la altitud afecta de forma diferente las variables termoeconómicas de los componentes del sistema, presentando la tendencia a que los costos no termodinámicos cobren mayor importancia con ésta.
- Para el caso colombiano los costos no termodinámicos pueden llegar a ser más importantes que en otros países, dados los costos de transporte que implica la ubicación de los pozos de gas natural respecto de las principales ciudades del país que están a grandes altitudes. Sin embargo, dicho efecto no es directamente proporcional a la altitud y por lo tanto no se incluyó en el estudio realizado.
NOMENCLATURA
A: Constante para el cálculo de los costos no termodinámicos [US$]
c: Costo exergético unitario [US$/kJ]
C: Compresor
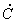 : Tasa de costo termodinámico [US$/s
: Tasa de costo termodinámico [US$/s
CC: Cámara de combustión
e: Exergía específica [kJ/kg]
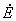 : Flujo exergético [kW]
: Flujo exergético [kW]
EV: Evaporador
f: Factor exergoeconómico
h: Entalpía específica [kJ/kg]
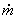 : Flujo másico [kg/s]
: Flujo másico [kg/s]
P: Presión [kPa]
PC: Precalentador
PCI: Poder calorífico inferior [kJ/kg]
PEC: Precio de compra [US$]
r: Diferencia de costos relativa
s: Entropía específica [kJ/kgK]
T: Temperatura [K], Turbina
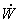 : Potencia mecánica [kW]
: Potencia mecánica [kW]
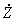 : Tasa de costos no termodinámicos [US$/s]
: Tasa de costos no termodinámicos [US$/s]
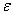 : Eficiencia exergética
: Eficiencia exergética
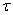 : Tiempo anual de funcionamiento de la planta [s]
: Tiempo anual de funcionamiento de la planta [s]
Subíndices
C: Compresor
CC: Cámara de combustión
D: Destrucción
e: Entrada
EV: Evaporador
F: Recurso
i: Especie componente de la mezcla de gases
k: Componente del sistema
L: Pérdidas
P: Producto
PC: Precalentador
Q: Calors: Salida
T: Turbina
tot: Total, relativo al sistema completo
W: Trabajo
0: Estado muerto
Superíndices
F: FísicaQ: Química
REFERENCIAS [ Links ] [2]














