Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
DYNA
versão impressa ISSN 0012-7353versão On-line ISSN 2346-2183
Dyna rev.fac.nac.minas v.74 n.152 Medellín maio/ago. 2007
SIMULACIÓN NUMÉRICA DEL CONTACTO DESLIZANTE PARA EL SISTEMA 2117-T4 / X19CRNI17.2 EN COMPRESIÓN UNIAXIAL
NUMERIC SIMULATION OF SLIDING CONTACT FOR THE SYSTEM 2117-T4 / X19CrNi17.2 IN MECHANICAL UPSETTING
HADER VLADIMIR MARTÍNEZ T.
Grupo de investigación sobre nuevos materiales, Universidad Pontificia Bolivariana, hader.martinez@upb.edu.co
LUIS JAVIER CRUZ R
Grupo de investigación sobre nuevos materiales, Universidad Pontificia Bolivariana, luis.cruz@upb.edu.co
Recibido para revisar 27 de Abril de 2006, aceptado 12 de Febrero de 2007, versión final 23 de Marzo de 2007
RESUMEN: Se reporta un estudio sobre el contacto deslizante entre una aleación de aluminio 2117-T4 y un acero inoxidable X19CrNi17.2 (AISI 431), el mismo es relevante en el caso de operaciones de deformación plástica. Teniendo en cuenta la geometría inicial de algunas de las probetas de ensayo, v.g. 7.14mm de longitud y 4.76mm de diámetro, fue seleccionado un ensayo de compresión uniaxial para la determinación de las condiciones tribológicas. El coeficiente de fricción de Coulomb existente en la interfase probeta-plato de compresión, para las condiciones experimentales que fueron consideradas, se halla entre 0.02 y 0.03.
PALABRAS CLAVE: Compresión uniaxial, tribología, coeficiente de fricción, simulación numérica.
ABSTRACT: A study on the sliding contact between a 2117-T4 aluminum alloy and a stainless steel X19CrNi17.2 (AISI 431) is reported. This interaction is important for the different operations of plastic deformation. Considering the initial geometry of the samples, i.e. 7.14mm of length and 4.76mm of diameter, it was selected a cylinder upsetting test for the determination of tribological conditions. For the experimental conditions used, the Coulomb friction coefficient found at the sample-compression plate interphase, was between 0.02 and 0.03.
KEYWORDS: Cylinder upsetting, tribology, friction coefficient, numeric simulation
1. INTRODUCCIÓN
La tendencia actual en el conformado mecánico de aleaciones de aluminio para forja, está caracterizada por una demanda creciente de formas complejas y tolerancias estrechas. La simulación numérica de las operaciones termomecánicas constituye en general una ayuda interesante para comprender la influencia de los parámetros de proceso sobre la calidad final del producto. La precisión de los resultados numéricos es sin embargo fuertemente dependiente de las propiedades del material y de las condiciones de fricción en la interfase con la herramienta de conformación. En tal sentido, numerosos modelos reológicos y unos cuantos a nivel tribológico han sido desarrollados para tener en cuenta tanto el flujo de material, como las condiciones de fricción. Tales modelos a menudo comprometen un variado número de parámetros, estimables a partir de ensayos mecánicos simples (tracción, compresión, torsión, pruebas de anillo, entre otros).
Para el caso particular de la aleación de aluminio para forja 2117-T4, una aleación comúnmente utilizada en la industria aeronáutica para la fabricación de remaches, se reporta en este artículo un estudio tribológico sobre el contacto deslizante con un acero inoxidable X19CrNi17.2 (AISI 431), de cara a la realización de procesos mecánicos de conformación plástica a bajas velocidades de deformación y temperatura. Teniendo en cuenta la geometría inicial de algunas de las probetas de ensayo, v.g. 7.14mm de longitud y 4.76mm de diámetro, fue seleccionado un ensayo de compresión uniaxial para la determinación de las condiciones tribológicas de contacto con los platos de compresión de la máquina de prueba.
El ensayo de compresión es pocas veces efectuado en materiales metálicos debido a que la resistencia a la tracción es generalmente la propiedad crítica y adicionalmente, porque en la mayoría de casos, la resistencia a compresión es superior o igual que la resistencia a tracción [1]. Sin embargo, en operaciones termomecánicas, el ensayo de compresión adquiere importancia porque el mismo es una herramienta útil cuanto se intenta definir el comportamiento reológico de un material [2], en función de la influencia que la fricción ejerce sobre el flujo plástico [3].
La fricción existente genera un embarrilamiento en el volumen de la muestra, provocando además un estado triaxial de esfuerzos, mientras que en la superficie libre es biaxial [4]. Así las cosas, la interpretación de los resultados del ensayo de compresión por métodos analíticos, como los usados convencionalmente en el ensayo de tracción, puede ser considerada sólo en el caso de que la fricción entre la pieza y los platos de compresión sea minimizada. Sin embargo, en ensayos de compresión uniaxial para muestras lubricadas y con relaciones de esbeltez de 1.5, la carga aplicada influencia fundamentalmente la reología del material y no mucho el valor del coeficiente de fricción, mientras que la geometría del cilindro deformado y relajado (embarrilamiento), es sensible a la fricción pero no mucho a la reología del material [5]. Con esta consideración, la reología y la tribología pueden ser identificadas independientemente, de manera que los valores de carga aplicada son usados para determinar parámetros reológicos, para cualquier tipo de condición de fricción, mientras que el valor del coeficiente de fricción, puede obtenerse a partir de la geometría de la probeta. En este segundo caso, es posible recurrir a la simulación numérica del ensayo, haciendo uso de una ley de comportamiento cuyos parámetros reológicos han sido provistos en el curso de la primera identificación.
En el estudio que aquí se reporta, una capa de lubricante sólido de MoS2 fue depositada en la interfase pieza/plato de compresión, con el fin de minimizar el coeficiente de fricción y aproximar un ensayo de compresión homogéneo (poco triaxial) tanto como fuera posible y, en el cual la fricción presente una mínima influencia en el flujo del material. Los aspectos tribológicos fueron entonces identificados a partir de la geometría de probetas deformadas mediante una aproximación inversa [6, 7] y con la ayuda de FORGE2®v3.0 para la simulación del ensayo de compresión. La ley de comportamiento utilizada para la aproximación numérica del flujo plástico de la aleación 2117-T4, fue una ley isótropa para un material que se ajusta al criterio de von Mises [8].
2. ASPECTOS TEÓRICOS
2.1. Modelos tribológicos
Lin [9] ha indicado que en la interfase pieza/plato de compresión, el coeficiente de fricción puede evolucionar durante un ensayo de compresión. Sin embargo, en la mayoría de casos el coeficiente de fricción se supone constante durante un proceso de deformación plástica.
Para tener en cuenta la fricción en una herramienta de simulación, es necesario disponer de un modelo que de cuenta del esfuerzo de cizallamiento interfacial. Dos modelos son comúnmente utilizados, el modelo de fricción de Coulomb y el modelo de fricción de Tresca [10]. En el modelo de fricción de Coulomb (Figura 1a), el esfuerzo tangencial t, es directamente proporcional al esfuerzo normal sn mediante el coeficiente de fricción de Coulomb m, el cual, es un coeficiente promedio (sobre la zona de contacto) e isótropo. Este modelo es generalmente válido para el caso de un contacto con sn moderado.
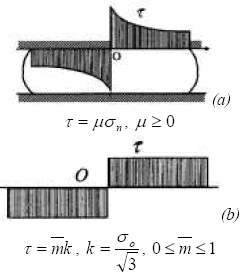
Figura 1. Modelos convencionales de fricción: (a) Modelo de Coulomb, (b) Modelo de Tresca [11]
Figure 1. Conventional friction models: (a) Coulomb model, (b) Tresca Model [11]
En el modelo de fricción de Tresca (Figura 1b), el esfuerzo tangencial está ligado al esfuerzo de deslizamiento en cizallamiento k, mediante el coeficiente de fricción de Tresca 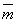 , el cual es un nuevo factor de fricción promedio. Este modelo es más utilizado para configuraciones de contacto con sn elevado. Si el material obedece al criterio de von Mises;
, el cual es un nuevo factor de fricción promedio. Este modelo es más utilizado para configuraciones de contacto con sn elevado. Si el material obedece al criterio de von Mises; 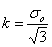 , donde so es el esfuerzo de fluencia del material obtenido en un ensayo mecánico. Si por el contrario el material obedece al criterio de Tresca;
, donde so es el esfuerzo de fluencia del material obtenido en un ensayo mecánico. Si por el contrario el material obedece al criterio de Tresca;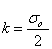 .
.
Un tercer modelo utilizado por Duan et-al. en simulaciones con FORGE3Ò [12], es un modelo interesante que considera la evolución del esfuerzo normal durante un proceso termomecánico. Este modelo de fricción de Coulomb limitado a Tresca, es ilustrado en (1) para el caso de un material que obedece el criterio de von Mises.
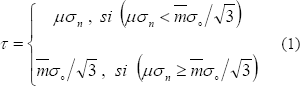
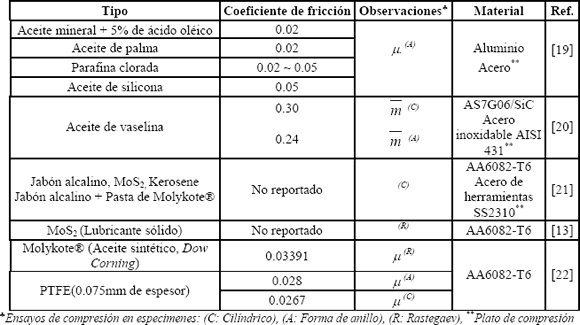
En general, el contacto es función de muchos parámetros (reología de los materiales presentes, estado superficial de cada uno y en el caso de superficies lubricadas, la reología del lubricante), de suerte que a pesar de la existencia de muchos modelos de fricción estos son aún aproximados, ya que tienen en cuenta de manera indirecta e imperfecta el conjunto de dichos parámetros. En la práctica, se utiliza un modelo de fricción que incluya ciertos parámetros fundamentales, las otras variables desconocidas son tomadas en consideración en el valor del coeficiente de fricción. Este valor puede ser obtenido a partir de la literatura técnica [13, 14-18, 19-22], ábacos [23], o incluso ayudándose de técnicas de análisis superficial [23]. La Tabla 1 resume algunos casos comunes en el caso de compresión uniaxial.
Tabla 1. Lubricantes usados en compresión uniaxial. Revisión
Table 1. Lubricants used in cylinder upsetting. Rerview
2.2. Modelos reológicos
Las aleaciones de aluminio y en particular aquellas de la serie 2000, presentan un comportamiento viscoplástico; a temperatura ambiente, el comportamiento es a menudo poco sensible a la velocidad de deformación [25], mientras que a temperatura elevada, los esfuerzos que denotan la zona plástica tienden a mantenerse casi constantes con el nivel de deformación, pero manifestando sensibilidad a la velocidad de deformación [19].
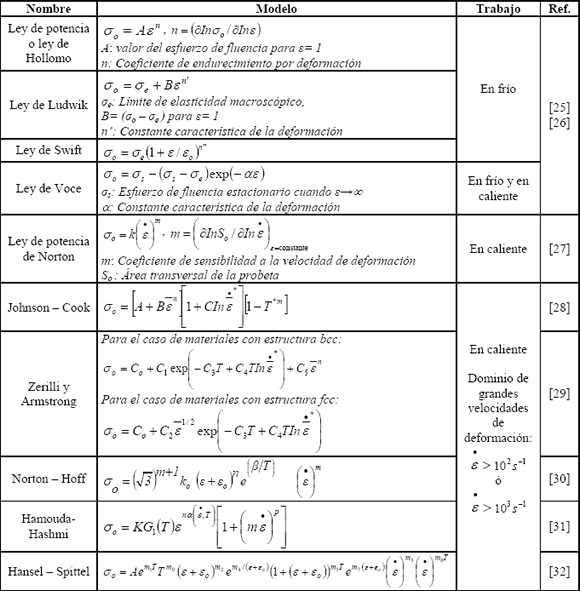
Numerosos modelos de deformación plástica están disponibles en la literatura, estos permiten relacionar el estado de tensiones o deformaciones, la temperatura y la velocidad de formación (Tabla 2).
Tabla 2. Modelos de deformación plástica para metales. Revisión
Table 2. Models for plastic deformation in metals. Review
2.1.1. Modelos de deformación plástica pura 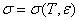
Estos son esencialmente utilizados para el trabajo en frío. Los resultados experimentales son en representados por relaciones del tipo: s= A1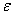 n, ó s=A2+ A1
n, ó s=A2+ A1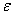 n, como en el caso de los modelos de Hollomon, Ludwik, Swift-Krupkowski, Voce [26] y Martínez-Coupard [8].
n, como en el caso de los modelos de Hollomon, Ludwik, Swift-Krupkowski, Voce [26] y Martínez-Coupard [8].
2.1.2. Modelos de viscosidad pura 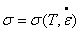
A alta temperatura se establece en general un equilibrio entre procesos de deformación plástica y de restauración. Los resultados experimentales pueden ser expresados por una relación de tipo potencia: s= A1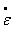 m (A1, m son funciones de la temperatura T), como en el modelo de Norton [27].
m (A1, m son funciones de la temperatura T), como en el modelo de Norton [27].
2.1.3. Modelos viscoplásticos, 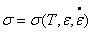
En la gama intermedia y elevada de 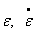 y T, se utiliza a menudo una relación de tipo potencia: s= A1
y T, se utiliza a menudo una relación de tipo potencia: s= A1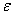 n
n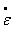 m (A1, n, m son funciones de la temperatura T), como en los modelos de Johnson-Cook [28], Zerilli-Armstrong [29], Norton-Hoff [30], Hamouda-Hashmi [31] y Hansel-Spittel [32].
m (A1, n, m son funciones de la temperatura T), como en los modelos de Johnson-Cook [28], Zerilli-Armstrong [29], Norton-Hoff [30], Hamouda-Hashmi [31] y Hansel-Spittel [32].
3. SIMULACIÓN NUMÉRICA DEL ENSAYO DE COMPRESIÓN
El software FORGE2® es un software que permite el cálculo termomecánico a grandes deformaciones de una pieza en contacto con una herramienta de forja, usando para ello una ley de comportamiento de Prandtl-Reuss [33]. El mallado utiliza elementos triangulares isoparamétricos de seis nodos y funciones de interpolación cuadráticas (dispone igualmente de un procedimiento de remallado automático). El cálculo utiliza una aproximación incremental lagrangiana y reactualizada (reactualización de variables de estado e, T, ) fundamentada en el principio de trabajo virtual, donde la resolución del sistema no lineal se efectúa por un algoritmo del tipo Newton-Raphson.
3.1. Ecuaciones de base
Para el caso que fue de interés en esta investigación, W(t) es el dominio de la pieza en el tiempo t, ∂Wc es la superficie de contacto y ∂Wn la superficie libre (Figura 2.). Las ecuaciones (2-4) denotan respectivamente el equilibrio mecánico, la incomprensibilidad plástica y el equilibrio térmico [5]:


Figura 2. Superficie libre y de contacto consideradas en compresión uniaxial
Figure 2. Free and contact surfaces considered in cylindrical upsetting
En estas ecuaciones s es el tensor de esfuerzos, v el campo de velocidades del flujo de materia, 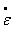 el tensor de velocidad de
el tensor de velocidad de
deformación, rC la capacidad calórica, l la conductividad térmica y 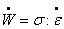 , la potencia plástica disipada.
, la potencia plástica disipada.
3.2. Condiciones de frontera
Las condiciones de frontera para el caso que se estudia comprenden tanto las referentes al problema mecánico como al problema térmico.
3.2.1. Condiciones mecánicas
Para un contacto unilateral pieza/plato de compresión, en el cual el movimiento de los nodos de la pieza no está permitido en la interfase, se tiene [34]:
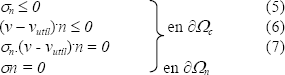
donde vutíl es la velocidad del plato móvil en la máquina de ensayos, sn el vector de esfuerzo normal y sn = sn.n es el esfuerzo normal.
3.2.2. Condiciones térmicas
Dos condiciones son usadas en los límites:
Una condición de flujo en ∂W :
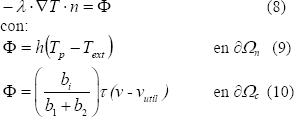
donde Tp es la temperatura de superficie de la pieza, Text, la temperatura exterior y h un coeficiente de intercambio global (convección y radiación). t es representado por la relación (1), b1 y b2 son las efusividades de la pieza y de la herramienta o plato de compresión respectivamente, bi = b1 ó b2 según se analice el plato o la pieza. Estas efusividades pueden calcularse como [35]:

Una condición de temperatura en ∂Wc :

3.3. Modelamiento
El componente tribológico está representado por el modelo de Coulomb limitado a Tresca (1). Una de dos condiciones de fricción particular puede ser utilizada. La primera concierne al contacto deslizante, especificando m = 0. La segunda, concierne a un contacto adhesivo, el cual no autoriza deslizamiento interfacial, con m 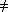 0, esta es la condición que ha sido utilizada. La parte elástica del tensor de esfuerzos es expresada a partir de la ley de Hooke:
0, esta es la condición que ha sido utilizada. La parte elástica del tensor de esfuerzos es expresada a partir de la ley de Hooke:
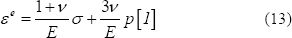
donde ee es el tensor de deformaciones elásticas, p= -0.33.traza(s) es la presión hidrostática y [1], el tensor unitario. Los valores de E y n son generalmente constantes pero pueden eventualmente depender de la temperatura mediante una ley de tipo Arrhenius:

donde b es un parámetro térmico.
Como hipótesis fundamental, se considera que el material es homogéneo, isótropo y que obedece al criterio de von Mises. Para los materiales metálicos, se puede considerar generalmente que su comportamiento reológico es independiente de la presión hidrostática. El esfuerzo equivalente en el sentido de von Mises no depende mas que de la parte deviatoria [s], ([s] =[s]+p[I]) del tensor de esfuerzos:

Considerando las tensiones principales s1, s2 y s3, el esfuerzo equivalente se expresa:
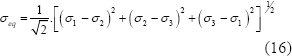
El desarrollo de la deformación plástica tiene lugar cuando seq=so, es decir, cuando: f=(seq-so)=0, donde f es la función de carga. Para expresar el límite de fluencia so, se ha utilizado una ley del tipo Hansel – Spittel, como la ilustrada en la Tabla 2.
4. DESARROLLO EXPERIMENTAL
Los ensayos de compresión fueron realizados en una máquina Adamel Lhomargy, equipada con una celda de carga de 100KN - clase 0.5 y un captor de desplazamiento inductivo de precisión ± 0.02mm (clase 0.5 en el curso de 4mm). El material de los platos de compresión de la máquina fue un acero inoxidable X19CrNi17.2 (AISI 431). Estos ensayos se efectuaron a dos velocidades de desplazamiento (vb= 1mm/min y vh= 60mm/min). En cuanto a la sensibilidad a la temperatura, se exploraron igualmente dos valores: Tb=
En este apartado, conviene aclarar que los tipos de probetas utilizadas típicamente en el ensayo de compresión son de geometría cilíndrica o plana, estas últimas son útiles para la validación de simulaciones en operaciones de laminación [24]. Algunos autores han utilizado probetas cilíndricas, tipo Rastegaev, que presentan cavidades en ambas caras, las cuales son usadas para reducir el efecto de embarrilamiento generado en el curso del ensayo de compresión [13].
En particular, los estándares ASTM E9 [36] y ASTM E209 [37], cubren las especificaciones técnicas para la realización de ensayos de compresión a temperatura ambiente y a temperatura elevada respectivamente. Para el caso que aquí se reporta, la norma ASTM E9 señala los siguientes aspectos:
4.1. Tipo de probeta
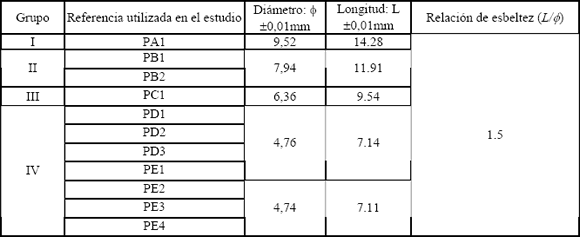
En la norma ASTM E9 se hace igualmente referencia a probetas cilíndricas, esta geometría se ha mantenido y para tal efecto, fueron utilizadas probetas cilíndricas de diámetro calibrado. El diámetro de fabricación de la probeta permite conservar el efecto histórico del trefilado, el cual afecta preferentemente la superficie y las zonas cercanas al exterior de la pieza. Adicionalmente, cada cara fue refrentada para un largo específico. La Tabla 3 lista las dimensiones finales de las probetas utilizadas en este estudio.
Tabla 3. Dimensiones de las muestra
Table 3. Dimensions of the samples
4.2. La relación de esbeltez (L/f)
Su magnitud no debe ser muy elevada para evitar el riesgo de flexión del elemento. Una relación comprendida entre 1.5 y 2.0 es sugerida para caracterizar la resistencia a la compresión. Una revisión hecha por los autores para el caso de caracterizar una ley de deformación plástica a partir de un ensayo de compresión [8], muestra en este caso que es común el uso de una relación de esbeltez de 1.5.
De manera complementaria, Forestier y colaboradores [5], han reportado que la relación L/f de 1.5 es más sensible a la reología que una de 0.75. Según los autores, en este segundo caso la fricción influencia de manera importante el flujo plástico. Así, para probetas cilíndricas con una relación de esbeltez L/f ³ 1.5, la fuerza permite la determinación de parámetros reológicos, considerando un coeficiente de fricción aproximado pero realista y la geometría del elemento por otro lado, permite la evaluación del coeficiente de fricción. Como se observa en la Tabla 3, en este estudio fue seleccionada una relación de esbeltez de 1.5. Bajo estas condiciones y de cara a una simulación del ensayo de compresión, el estudio tribológico que aquí se reporta fue realizado de manera independiente al estudio reológico particular del material.
4.3. Geometría de la muestra y acabado superficial
En el caso de probetas cilíndricas, ciertos defectos geométricos (Figura 3), deben ser minimizados para obtener una distribución homogénea de la carga durante el desarrollo de una prueba de compresión.
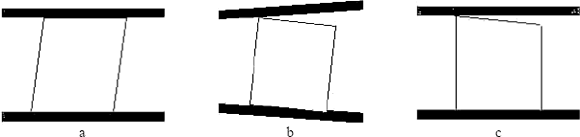
Figura 3. Algunos defectos geométricos del conjunto plato de compresión-probeta de ensayo durante el curso de un ensayo de compresión: (a) Defecto de perpendicularidad, (b) no paralelismo de platos, (c) no paralelismo de caras opuestas de la muestra
Figure 3. Several geometrical defects in cylinder upsetting: (a) Perpendicularity defect, (b) Non-parallelism, (c) Non-parallelism between opposite faces of the sample
De otro lado, la norma sugiere que las caras opuestas de la muestra deben poseer un acabo tan fino como sea posible, con una rugosidad como máximo de 1.6µm, sin precisar si se trata de Ra absoluta o de otro parámetro.
4.5. Paralelismo de las caras opuestas
Este debe ser el mejor posible. La norma sugiere una precisión de 0.0005mm/mm, lo que corresponde, sobre una muestra de diámetro 4.8mm, a un defecto de paralelismo de máximo 0.2 centésimas de mm. Éste valor es difícil de asegurar y para el caso que fue estudiado, el mismo es del orden de una centésima.
4.6. Lubricación
Es claro que no se dispone actualmente de medios que permitan obtener una fricción nula en la interfase probeta-plato de compresión. Bajo esta condición, experimentalmente es conveniente limitar la fricción interponiendo una capa que juegue el rol de lubricante sólido o asumir que la interfase es de tipo adhesivo. En este estudio fue seleccionada la óptica de la minimización del coeficiente de fricción. La lubricación sugerida por la norma es de tipo PTFE ó MoS2. En éste caso, se seleccionó un spray seco MolykoteD321Ò a base de bisulfuro de Molibdeno (MoS2).
5. INFLUENCIA DE LA FRICCIÓN SOBRE LA CURVA FUERZA-DESPLAZAMIENTO
Como ejemplo, se reporta aquí el estudio desarrollado sobre las probetas de referencia PE1 (Tabla 3). Los parámetros utilizados para la ley de tipo Hansel-Spittel simplificada (Tabla 2), son: A= 670MPa, m2 = 0.24, m7 = -0.12. El coeficiente de fricción µ, se ha limitado a un máximo de 0.1 (se considera que el uso de Molykote® no dará lugar a coeficientes de fricción superiores según lo indicado en la Tabla 1).
En un intento de simplificación, se utilizó 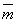 = 1, lo cual equivale a considerar que t se iguala al valor del esfuerzo de deslizamiento en cizallamiento
= 1, lo cual equivale a considerar que t se iguala al valor del esfuerzo de deslizamiento en cizallamiento 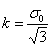 . Si la diferencia geométrica de la probeta deformada experimentalmente y la probeta teórica hubiera sido significativa, habría sido necesario limitar igualmente el valor de
. Si la diferencia geométrica de la probeta deformada experimentalmente y la probeta teórica hubiera sido significativa, habría sido necesario limitar igualmente el valor de  .
.
En las Figuras 4a-4c se presentan las curvas experimentales fuerza-desplazamiento de tres probetas (Ref. PE1-03, PE1-06 y PE1-07), ensayadas a velocidades de desplazamiento de 1mm/min y temperatura ambiente (
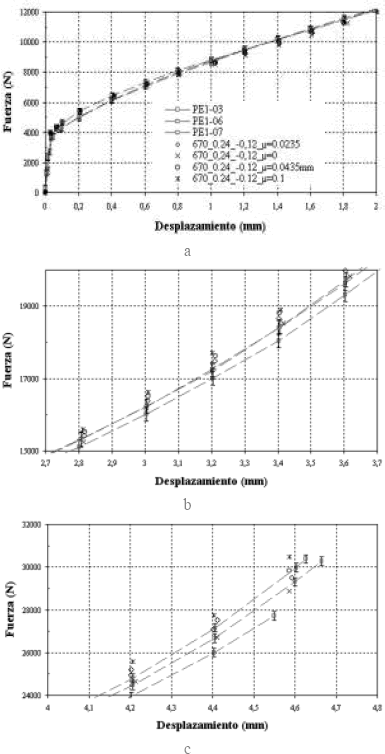
Figura 4. Influencia del coeficiente de fricción sobre la curva fuerza-desplazamiento (vb, Tb): (a) 0kN-12kN, (b) 15kN-20kN y (c) 24kN-32kN
Figure 4. Effect of the friction coefficient on the force-displacement curve (vb, Tb): (a) 0kN-12kN, (b) 15kN-20kN y (c) 24kN-32kN
Para la gama estudiada del coeficiente de fricción (µ< 0.1), la influencia que el mismo presenta sobre la curva fuerza-desplazamiento es despreciable excepto para desplazamientos importantes (> 3mm; i.e. ereal > 55% para una probeta de altura inicial L= 7.14mm).
Diferentes ensayos ulteriores, mostraron que m es en promedio bastante estable de un ensayo a otro. Así, la comparación de puntos obtenidos con µ= 0.0235 y µ= 0.0435, muestra que la fricción no modifica la forma de la curva fuerza-desplazamiento para ereal < 50%. El enunciado de Forestier es entonces válido en este caso, teniendo en cuenta la pequeña variación de µ entre cada ensayo.
6. INFLUENCIA DE LA FRICCIÓN SOBRE LA GEOMETRÍA FINAL DE LA PROBETA
Con el fin de determinar la incidencia del coeficiente de fricción sobre la forma final de la probeta deformada, se procedió entonces a comparar las características dimensionales tanto teóricas (obtenidas por simulación en FORGE2®) como experimentales de redondos deformados y relajados (luego de retirarlos de los platos de la máquina). Las características dimensionales consideradas fueron los diámetros superior, inferior y máximo o meridional.
La Figura 5 muestra la variación geométrica de dos probetas (Ref. PE2-02 y PE2-03). En las abscisas se encuentra la altura del redondo relajado y en las ordenadas, el diámetro de la probeta. x = 0, corresponde a la posición de la sección de la probeta en contacto con el plato de compresión inferior. El punto más elevado de las abscisas corresponde a la posición de la probeta relajada en contacto con el plato de compresión superior luego de realizado el ensayo. Finalmente, el punto intermedio corresponde a la posición hasta la cual se extiende la sección máxima de la probeta deformada por efecto del fenómeno de embarrilamiento.
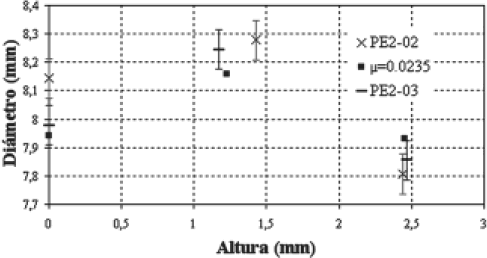
Figura 5. Influencia del coeficiente de fricción sobre la geometría final de las probetas usando un solo coeficiente de fricción (vb, Tb)
Figure 5. Effect of the friction coefficient on final geometry of the samples with one friction coefficient (vb, Tb)
Experimentalmente los diámetros y la altura final fueron medidos con una precisión de ±0.001mm. Para cada dimensión y cada referencia de las probetas, se efectuaron cinco medidas con el fin de estimar una desviación tipo de la precisión de medida, la cual en promedio fue de ±0.1 para todas las dimensiones.
Las características dimensionales medidas en las probetas PE2-02 y PE2-03 (Figura 5), presentan una desviación a nivel de los diámetros extremos. Por el contrario, la simulación efectuada con un valor idéntico del coeficiente de fricción en ambos platos (µ= 0.0235), muestra valores idénticos en los diámetros superiores e inferiores. En consecuencia, es posible concluir que la fricción no es igual en ambos platos.
Para disminuir esta diferencia es necesario adaptar el valor del coeficiente de fricción según se trate del plato superior o inferior. La Figura 6 muestra los resultados obtenidos al considerar una fricción diferente sobre ambos platos. Se observa que los valores: minf = 0.01-msup= 0.03, pero principalmente la dupla: minf = 0.02-msup= 0.03, correlacionan bastante bien los resultados experimentales. La pareja: minf = 0,06-msup= 0.1 por otro lado, presenta coeficientes relativamente bajos en valor, pero elevados con relación a las otras dos configuraciones, dejando ver claramente diferencias con relación a los resultados experimentales.
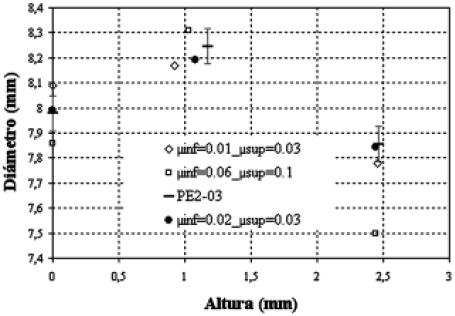
Figura 6. Influencia de diferentes coeficientes de fricción sobre la geometría de la probeta (vb, Tb)
Figure 6. Effect of different friction coefficient on final geometry sample (vb, Tb)
La Figura 7 presenta dos probetas deformadas y relajadas y la Figura 8 es la imagen de la probeta PE1 genérica, cuya deformación ha sido simulada en FORGE2®. La probeta de la Figura 7a fue deformada sin el uso de lubricante, mientras que la mostrada en la Figura 7b (PE1), fue deformada interponiendo una capa de Molykote® como lubricante. Se observa claramente un efecto de embarrilamiento más marcado sobre la probeta de la Figura 7a. y una similitud entre las Figuras 7b y 8.

Figura 7. Influencia de la fricción sobre la geometría final de la probeta deformada: (a) sin el uso de lubricante, (b) lubricación con Molykote®
Figure 7. Effect of the friction coefficient on final geometry of the deformed sample: (a) No lubricant, (b) Molykote® lubricant
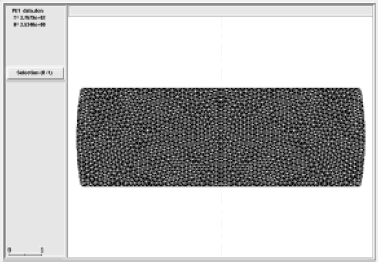
Figura 8. Simulación en FORGE2®. de una probeta ref. PE1 (vb, Tb, µinf = µsup= 0,023), (dimensiones en mm)
Figure 8. Simulation in FORGE2®. Sample ref. PE1 (vb, Tb, µinf = µsup= 0,023), (dimensions in mm)
7. CONCLUSIONES
- Se ha podido establecer el cálculo del coeficiente de fricción de Coulomb por métodos analíticos derivados de un ensayo de compresión uniaxial.
- Es posible argumentar que para el caso estudiado, la fricción posee una influencia despreciable sobre la curva fuerza-desplazamiento. Por el contrario, la misma influye fuertemente en las características dimensionales del elemento deformado.
- El coeficiente de fricción de Coulomb existente en la interfase probeta-plato de compresión para las condiciones experimentales asumidas (material de trabajo y de los platos: aleación de aluminio 2117-T4 e inoxidable X19CrNi17.2 respectivamente, y un agente lubricante: spray seco a base de MoS2, Molykote D321Ò), se halla entre: 0.02 y 0.03.
- Para valores del coeficiente de fricción de Coulomb inferiores a 0.04 y una relación de forma de 1.5, la reología y la tribología pueden ser identificadas separadamente en concordancia con el planteamiento propuesto por Forestier.
REFERENCIAS [ Links ] [2]














