Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
DYNA
versão impressa ISSN 0012-7353versão On-line ISSN 2346-2183
Dyna rev.fac.nac.minas v.74 n.153 Medellín set./dez. 2007
SISTEMA DE ADQUISICIÓN DE IMÁGENES DE RANGO CON BASE EN ESTÉREO-ACTIVO
A RANGE IMAGE ACQUISITION SYSTEM BASE ON ACTIVE-STEREO
AUGUSTO SALAZAR
Departamento de Ingeniería Eléctrica, Electrónica y Computación, Universidad Nacional de Colombia, aesalazarj@unal.edu.co
LUIS GONZALO SANCHEZ
Departamento de Ingeniería Eléctrica, Electrónica y Computación, Universidad Nacional de Colombia, Sede Manizales
FLAVIO PRIETO
Departamento de Ingeniería Eléctrica, Electrónica y Computación, Universidad Nacional de Colombia, Sede Manizales
Recibido para revisar noviembre 04 de 2006, aceptado febrero 26 de 2007, versión final abril 19 de 2007
RESUMEN: En el presente trabajo, se describe un sistema estéreo activo para la adquisición de imágenes de rango de bajo costo implementado sobre MATLAB®. El sistema combina métodos de estimación de parámetros para dos vistas (tanto calibradas como no calibradas). En principio el sistema se considera no calibrado por lo que las orientaciones de las cámaras se desconocen. Al capturar un patrón de referencia se procede a estimar la matriz fundamental F y las matrices de cámara P1 y P2, que establecen la configuración espacial y otros parámetros. Se utiliza una versión modificada del algoritmo Gold Standard para la estimación de F. Para la adquisición de objetos reales, se restringe el área de búsqueda de correspondencias a líneas proyectadas sobre el objeto. Al tener dos imágenes de la línea proyectada no es necesario tener consideraciones especiales sobre la posición y geometría de la fuente de luz estructurada (rayo láser). Sin embargo algunas consideraciones sobre el ruido en la estimación de las correspondencias son necesarias para establecer la precisión del sistema.
PALABRAS CLAVE: estéreo, calibración de cámara, geometría epipolar, reconstrucción 3D.
ABSTRACT: In the present work, we describe a low cost active system to acquire range images implemented on MATLAB®. The system combines parameter estimation techniques when two views are provided (uncalibrated methods are considered as well as calibrated methods). We start by defining an uncalibrated system where camera orientations and positions are mainly unknown. After capturing a calibration rig by two uncalibrated cameras, we can estimate the fundamental matrix F and the two camera matrices P1 and P2. This matrices combined establish the spatial configuration of the setup and other relevant parameters. To acquire real objects, we constrain the search area for finding correspondences in two views by simply projecting a line onto the object. Since two views of the object are available, no considerations about calibration and position estimation of the structured light source are necessary. Nevertheless, considerations about noisy estimation of correspondences are necessary to assess the systems accuracy.
KEYWORDS: stereo, camera calibration, epipolar geometry, 3D reconstruction.
1. INTRODUCCIÓN
Para la adquisición de imágenes de rango se distinguen dos tipos fundamentales de sistemas, los sistemas que emiten energía a la escena para su adquisición (sistemas activos), y los sistemas pasivos que no requieren de la emisión de energía. En [1] muchos de los sistemas de adquisición activos descritos utilizan una
Cámara, aunque su precisión es notable, las consideraciones para su implementación hacen que su costo sea elevado. Dentro de los sistemas de adquisición activos se encuentran los escáner de corte (slit scanner) que se distinguen por ser los más económicos y ampliamente usados, sin embargo, al utilizar una sola cámara se deben conocer parámetros tales como la posición de la línea proyectada la posición exacta de la fuente de luz y la cámara, también. Además la línea o patrón proyectado requiere de una geometría muy controlada (la línea debe ser totalmente recta, etc). Dentro de los sistemas pasivos, los aplicaciones más comunes hacen uso de múltiples vistas del objeto para establecer las posiciones 3D de puntos que representan su superficie.
Los sistemas estéreo, que generalmente son de carácter pasivo (no emiten energía), se basan en algoritmos elaborados para definir puntos emparejados (correspondencias) en un par de imágenes. En general los puntos que se escogen corresponden a bordes o esquinas de los objetos y por ende las superficies con cambios suaves usualmente no son detectadas. La cantidad de puntos no es suficiente como para generar un modelo completo de la superficie visible del objeto.
En este trabajo, se describe una configuración para construir modelos 3D utilizando una combinación entre estéreo y una fuente de luz estructurada (línea de corte), que restringe el problema de búsqueda de correspondencias mientras que las consideraciones sobre la fuente de luz no son tan estrictas como lo deben ser para una sola cámara. El trabajo comienza con la descripción de las etapas del sistema hasta obtener la nube de puntos del objeto, luego se presentan y discuten algunos resultados de implementación que se confrontan con valores
Obtenidos a partir de la simulación completa del sistema estéreo; seguido de las conclusiones y trabajo futuro.
Notación.Para la presentación de los algoritmos de procesamiento, las cámaras reales se denotan como P1 y P2 , mientras que las realizaciones se definen como P'1 y P'2. Las correspondencias son
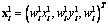 y
y 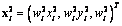 y los puntos 3D
y los puntos 3D 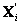 y
y 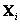 son las versiones distorsionadas y reales respectivamente. Sí cualquier elemento D sin importar que sea matriz o vector está normalizado por T, este se denota como
son las versiones distorsionadas y reales respectivamente. Sí cualquier elemento D sin importar que sea matriz o vector está normalizado por T, este se denota como 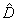 . Para un vector
. Para un vector 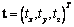 , su matriz simétrica oblicua viene dada por:
, su matriz simétrica oblicua viene dada por: 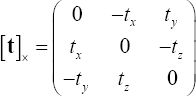
2. GEOMETRÍA DE DOS VISTAS
En la geometría de dos vistas, es posible calcular correspondencias y triangular los puntos 3D mediante la matriz fundamental F que relaciona las dos cámaras. En [2], se propone un algoritmo para estéreo a partir de vistas no calibradas; el algoritmo se basa en la propiedad donde dos pares de cámaras P1, P2 y P'1, P'2, que poseen la misma matriz F, están relacionadas por la matriz de transformación H como: P1=P'1H y P2=P'2H. Así, es posible calcular una realización de un par de cámaras que si bien no son las matrices reales P1 y P2 están relacionabas por la misma matriz fundamental y de ellas podemos obtener puntos tridimensionales Xd, que son producto de la transformación proyectiva de las posiciones reales X, por lo que Xd=HX.
3. MODELO DE CAMARA, IMÁGENES SINTETICAS Y ESTIMACION
Para probar los algoritmos de reconstrucción de la escena y estimación de parámetros, se construye un modelo de un par de cámaras en un escenario sintético que contiene un conjunto de puntos de evaluación. El modelo de cámara aquí usado, corresponde a la matriz 3×4 P, sin consideraciones de distorsión radial o alguna otra no linealidad.
La matriz P se construye como se muestra a continuación:
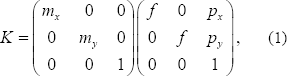
siendo 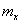 ,
, 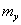 el radio de píxeles por unidad de medida en el mundo,
el radio de píxeles por unidad de medida en el mundo, 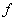 la distancia focal, y
la distancia focal, y 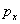 ,
, 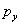 la distancia del centro de la imagen al origen de las coordenadas del plano imagen. El parámetro de oblicuidad
la distancia del centro de la imagen al origen de las coordenadas del plano imagen. El parámetro de oblicuidad 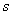 se adiciona haciendo
se adiciona haciendo 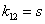 . Así, entonces queda conformado el conjunto de parámetros intrínsecos de la cámara. La posición y orientación de la cámara (parámetros extrínsecos) se definen a continuación. Para definir los parámetros extrínsecos de la cámara, se debe comenzar definiendo los sistemas de coordenadas de la cámara y el mundo (Figura 1).
. Así, entonces queda conformado el conjunto de parámetros intrínsecos de la cámara. La posición y orientación de la cámara (parámetros extrínsecos) se definen a continuación. Para definir los parámetros extrínsecos de la cámara, se debe comenzar definiendo los sistemas de coordenadas de la cámara y el mundo (Figura 1).
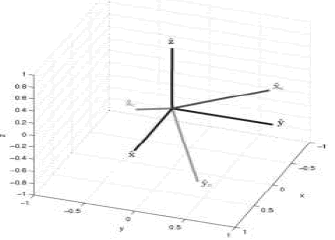
Figura 1. Sistemas de coordenadas de la cámara y el mundo.
Figure 1. Camera and world’s coordinate systems.
El eje 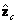 define la línea principal de la cámara, el plano
define la línea principal de la cámara, el plano 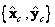 es el plano principal,
es el plano principal, 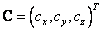 es el centro de cámara. Para propósitos prácticos, se restringen los parámetros de orientación, al definirlos automáticamente. La cámara apunta inicialmente al origen del sistema mundo, y así
es el centro de cámara. Para propósitos prácticos, se restringen los parámetros de orientación, al definirlos automáticamente. La cámara apunta inicialmente al origen del sistema mundo, y así 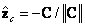 ,
, 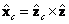 y
y 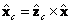 . Hasta este momento
. Hasta este momento 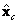 ,
, 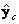 y
y 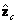 tienen el mismo origen que el sistema mundo, lo cual es útil para definir un conjunto de ángulos de rotación {θx, θy, θz} que completan la construcción de la matriz de rotación
tienen el mismo origen que el sistema mundo, lo cual es útil para definir un conjunto de ángulos de rotación {θx, θy, θz} que completan la construcción de la matriz de rotación 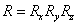 . Estos ángulos se definen a continuación:
. Estos ángulos se definen a continuación:
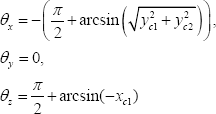
y las correspondientes matrices de rotación.
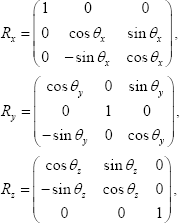
Completando así la matriz de cámara:
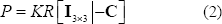
Un vez se tiene la matriz P se pueden proyectar los puntos 3D 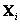 sobre el plano imagen en los puntos
sobre el plano imagen en los puntos 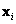 . La Figura 2(a) muestra la configuración de la escena y la Figura 2(b) las imágenes resultantes para dos cámaras con los mismos parámetros intrínsecos, pero en posiciones diferentes.
. La Figura 2(a) muestra la configuración de la escena y la Figura 2(b) las imágenes resultantes para dos cámaras con los mismos parámetros intrínsecos, pero en posiciones diferentes.
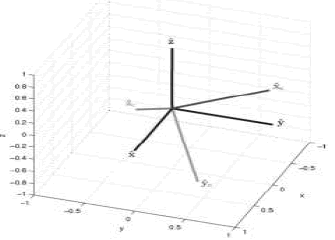
Figura 2. Configuración espacial de la cámara e imágenes resultantes.
Figure 2. Spatial configuration of cameras, and their resulting images.
Se tiene así, un conjunto de puntos conocidos que son correspondencias sobre las cuales es posible iniciar la estimación. En [3], se muestra como es posible calcular la matriz F con un conjunto dado de correspondencias de al menos 8 pares de puntos, condicionando el problema al normalizar los valores que componen el conjunto de ecuaciones. Para un par de correspondencias 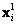 y
y 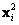 , donde
, donde 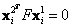 , el problema se puede reescribir como:
, el problema se puede reescribir como:

Para 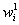 ,
, 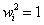 cuando se trata de posiciones de píxeles, se normalizan los datos a través de transformaciones isotrópicas
cuando se trata de posiciones de píxeles, se normalizan los datos a través de transformaciones isotrópicas 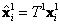 y
y 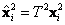 , que centran los datos en el origen {0,0} y se escala la distancia promedio a
, que centran los datos en el origen {0,0} y se escala la distancia promedio a 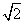 [3]. Nótese que los cálculos de estas normalizaciones se hacen para los vectores bidimensionales sin considerar el tercer elemento, los cuales permanecen iguales a 1. La Ecuación 3 se reescribe con los términos normalizados
[3]. Nótese que los cálculos de estas normalizaciones se hacen para los vectores bidimensionales sin considerar el tercer elemento, los cuales permanecen iguales a 1. La Ecuación 3 se reescribe con los términos normalizados
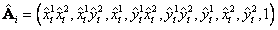 y
y 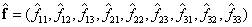 , así
, así 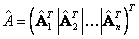 . La solución
. La solución 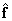 se pude obtener fácilmente a través de los multiplicadores de Lagrange como el último autovector de
se pude obtener fácilmente a través de los multiplicadores de Lagrange como el último autovector de 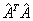 . Una vez
. Una vez 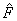 es reconformada, se impone la restricción de hacer su rango igual a 2, que se consigue al descomponer la matriz en valores singulares
es reconformada, se impone la restricción de hacer su rango igual a 2, que se consigue al descomponer la matriz en valores singulares 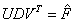 y hacer el tercer elemento de la matriz diag (D) igual a 0. La matriz de rango 2 se desnormaliza,
y hacer el tercer elemento de la matriz diag (D) igual a 0. La matriz de rango 2 se desnormaliza,

Con este estimado de F, se tiene un punto de partida para optimizar sus valores utilizando el algoritmo Gold Standard que minimiza la función de costo:
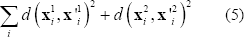
Escogiendo las realizaciones de cámara como 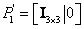 y
y 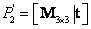 ; siendo inicialmente
; siendo inicialmente 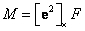 y
y 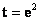 , es posible hacer un estimado inicial de los puntos 3D
, es posible hacer un estimado inicial de los puntos 3D 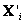 , y
, y 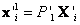 ,
, 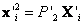 son usados para la primer iteración. El algoritmo optimiza 3n + 12 variables, 12 para
son usados para la primer iteración. El algoritmo optimiza 3n + 12 variables, 12 para 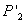 y 3n para los n puntos 3D
y 3n para los n puntos 3D 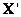 . La optimización corresponde a un método de mínimos cuadrados no lineal, por ejemplo Levenberg-Marquardt. Finalmente se halla
. La optimización corresponde a un método de mínimos cuadrados no lineal, por ejemplo Levenberg-Marquardt. Finalmente se halla 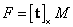 . Este algoritmo se considera óptimo porque
. Este algoritmo se considera óptimo porque 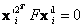 [4]. Sin embargo, algunas dificultades se pueden presentar durante su implementación. En este trabajo se considera una modificación al algoritmo que parece funcionar mejor.
[4]. Sin embargo, algunas dificultades se pueden presentar durante su implementación. En este trabajo se considera una modificación al algoritmo que parece funcionar mejor.
4. EL ALGORITMO GOLD STANDARD MODIFICADO
El algoritmo Gold Standard para la estimación de la matriz fundamental discutido en la Sección 3, presenta algunos problemas durante la optimización, y aunque el error fue minimizado como era de esperar 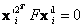 , los 3n puntos 3D
, los 3n puntos 3D 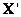 obtenidos, no corresponden a
obtenidos, no corresponden a 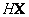 . La Figura 3(a) muestra los puntos 3D resultantes de las correspondencias mostradas en la Figura 2(b). Resulta obvio como la reconstrucción del objeto dista de ser la solución esperada y como el valor medio para
. La Figura 3(a) muestra los puntos 3D resultantes de las correspondencias mostradas en la Figura 2(b). Resulta obvio como la reconstrucción del objeto dista de ser la solución esperada y como el valor medio para 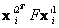 es
es 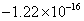 , que es muy cercano a 0.
, que es muy cercano a 0.
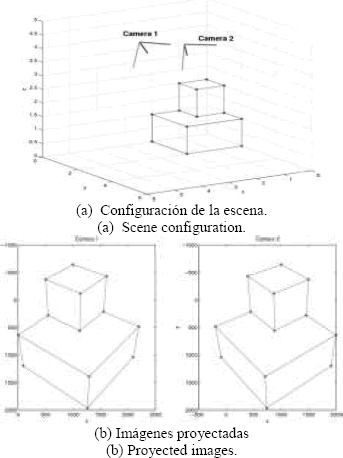
Figura 3. Puntos 3D resultantes para los mismos parámetros de cámara.
Figure 3. Resulting 3D points using the same camera parameters.
Se pudo observar como las soluciones dadas por los algoritmos de estimación lineal eran coherentes aunque sobre una proyectiva con el objeto original, pero dicha coherencia desaparecía al hacer la corrección de escala de los puntos 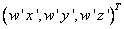 multiplicando por
multiplicando por 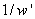 . Por tal motivo se propone la modificación del algoritmo Gold Standard incrementando el número de variables a optimizar y adicionando algunas normalizaciones.
. Por tal motivo se propone la modificación del algoritmo Gold Standard incrementando el número de variables a optimizar y adicionando algunas normalizaciones.
4.1 Las Modificaciones
La inicialización del algoritmo Gold Standard considera la previa estimación lineal de puntos 3D, al utilizar las realizaciones de cámara obtenidas de la matriz F calculada mediante cualquier estimación lineal como el algoritmo de 8 puntos, además, debe notarse que la matriz utilizada no está normalizada. Para nuestro algoritmo, la estimación de los puntos 3D se obtiene de las realizaciones de cámara a partir de la matriz 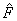 . De ésta manera
. De ésta manera  y
y 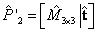 ; siendo inicialmente
; siendo inicialmente 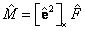 y
y 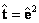 . Lo anterior implica que se estimará
. Lo anterior implica que se estimará 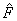 , tal que
, tal que 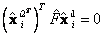 . Además de las consideraciones de datos normalizados, se hace uso de coordenadas que aún no han sido deshomogenizadas, es decir que para la optimización el número de variables se incrementa en n, para un total de 12+4n variables. Los puntos 3D no necesitan ser desnormalizados. Los
. Además de las consideraciones de datos normalizados, se hace uso de coordenadas que aún no han sido deshomogenizadas, es decir que para la optimización el número de variables se incrementa en n, para un total de 12+4n variables. Los puntos 3D no necesitan ser desnormalizados. Los 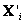 estimados se transforman a las posiciones reales mediante la matriz H, al igual que
estimados se transforman a las posiciones reales mediante la matriz H, al igual que 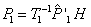 y
y 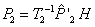 . Los puntos resultantes se muestran en la figura 3(b) y el error medio para
. Los puntos resultantes se muestran en la figura 3(b) y el error medio para 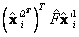 es
es 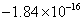 . A continuación se describen los pasos del algoritmo:
. A continuación se describen los pasos del algoritmo:
- Obtener un estimado inicial de
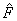 a partir del la ecuación (3) teniendo en cuenta la utilización de
a partir del la ecuación (3) teniendo en cuenta la utilización de 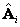 (datos normalizados).
(datos normalizados). - Encontrar estimados iniciales de los
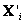 en coordenadas homogéneas mediante las realizaciones de cámara
en coordenadas homogéneas mediante las realizaciones de cámara  y
y 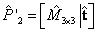 ; donde
; donde 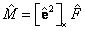 y
y 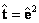 . El vector
. El vector 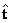 corresponde al espacio nulo de
corresponde al espacio nulo de 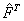 .
. - Optimizar los valores de
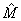 ,
, 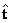 y
y 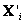 minimizando la función objetivo presentada en la ecuación (5), teniendo en cuenta que los puntos proyectados sobre los planos imagen se encuentran normalizados.
minimizando la función objetivo presentada en la ecuación (5), teniendo en cuenta que los puntos proyectados sobre los planos imagen se encuentran normalizados. - Encontrar la matriz H mediante el uso de puntos de referencia
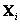 con posiciones conocidas en el espacio 3D tal que
con posiciones conocidas en el espacio 3D tal que 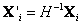 .
. - Desnormalizar las matrices de cámara a través de
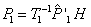 y
y 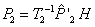 .
.
5. DESCRIPCIÓN DEL SISTEMA
El sistema propuesto es una combinación de un sistema activo, tipo escáner de corte, pero la estimación de la escena se basa en algoritmos de dos vistas (estéreo). Al utilizar un sistema activo es posible obtener más puntos de correspondencia para generar el modelo del objeto.
El sistema de adquisición consta de dos cámaras Web con resolución 640×480 píxeles. La fuente de luz estructurada se obtiene a partir de un haz de láser de diodo de bajo costo, que pasa por un elemento refractor, haciendo que este se proyecte como una línea. Un motor de paso se encarga de mover un espejo que refleja el haz láser, haciendo posible el barrido del objeto a adquirir. La sincronización, entre barrido y el par de imágenes analizadas, se logra a través de la comunicación serial entre el dispositivo de barrido y el computador que toma las imágenes y se encarga del resto del proceso. La Figura 4(a) muestra un esquema del sistema completo. La aplicación está desarrollada en MatLab®. En la Figura 4(b) se muestra una imagen del sistema.
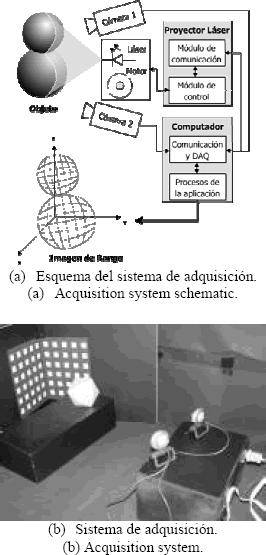
Figura 4. Cámara de rango.
Figure 4. Range camera.
La aplicación puede ser dividida en 4 rutinas principales: i) calibración del sistema, ii) adquisición de imágenes y procesamiento, iii) estimación de correspondencias y, iv) reconstrucción de la escena. Estas rutinas se detallarán en los siguientes párrafos.
5.1 Calibración
Tal como se muestra en la Figura 4, las cámaras no están fijas al sistema, por lo que cada vez que se quiere adquirir un objeto es necesario conocer sus posiciones. Dicho proceso se conoce como calibración del sistema y se puede hacer de diferentes maneras: los parámetros de cada cámara pueden ser estimados de forma individual y una vez conocidos, se estima la geometría epipolar de la escena. La geometría epipolar del sistema se puede estimar directamente y de allí obtener las calibraciones de cámara. Para esta aplicación se utiliza la segunda opción. Así, la calibración del sistema corresponde a la estimación de las matrices F y H, basado en un algoritmo de estéreo no calibrado, tales matrices son un compendio de la geometría del montaje. Como se describió en la Sección 4, es posible obtener las matrices de cámara reales 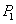 y
y 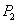 , a partir de F y H. Las matrices de cámara serán útiles más adelante. El estéreo a partir de vistas no calibradas parte de un conjunto de puntos 3D conocidos. Para ello se utiliza un patrón de calibración donde todas las posiciones de los puntos son bien conocidas.
, a partir de F y H. Las matrices de cámara serán útiles más adelante. El estéreo a partir de vistas no calibradas parte de un conjunto de puntos 3D conocidos. Para ello se utiliza un patrón de calibración donde todas las posiciones de los puntos son bien conocidas.
Los puntos usados como correspondencias son las esquinas de los cuadrados de la malla de calibración.
El proceso de encontrar las esquinas se puede resumir en los siguientes pasos:
- Umbralizar las imágenes de los patrones de calibración.
- Encontrar las regiones conectadas con ciertas consideraciones de área (segmentar los cuadrados del arreglo), y obtener sus perímetros.
- Para cada perímetro encontrar el rectángulo más pequeño que lo contenga.
- Los cuatro puntos más cercanos del perímetro a este rectángulo deben ser las esquinas de los cuadrados (Figura 5).
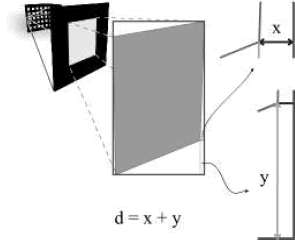
Figura 5. Parámetros para la extracción de las esquinas.
Figure 5. Parameters for corner extraction.
La Figura 6 muestra las imágenes reales con los puntos extraídos y su reconstrucción 3D después de encontrar F y H.
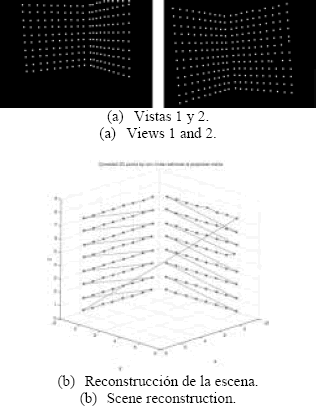
Figura 6. Esquinas reconstruidas a partir de las imágenes del patrón de calibración.
Figure 6. Reconstructed corners from images (views) of the calibration rig.
5.2 Adquisición y Procesamiento de las Imágenes
Las imágenes adquiridas están en RGB. Se asume que durante la adquisición no habrá un cambio drástico en la iluminación, y que la fuente de luz estructurada es simétrica, es decir que tiene una distribución normal. Se propone el siguiente algoritmo para la segmentación de la línea de barrido:
- La última imagen de la secuencia de adquisición es tomada como imagen de referencia (Iref).
- Iref y la imagen a segmentar (Iseg), son transformadas al espacio de color YCbCr.
- Se calcula la diferencia de la dos imágenes, como Idif = Iseg-Iref .
- Mediante la combinación de la componentes Y y Cr, se logra el realce de la línea de barrido, obteniendo una nueva imagen resultado de Ienh=Y+Cr .
- Ienh es umbralizada dejando sólo los píxeles que superen un valor de intensidad.
- De la imagen umbralizada, se obtiene la máscara que determina cuales de las coordenadas de la imagen Iseg serán analizadas.
- Puesto que la línea de barrido es aproximadamente vertical, se realiza una estimación de la posición horizontal de la línea, para esto se asignan pesos a las coordenadas donde prevalece el color rojo. El punto que se toma como muestra corresponde a la media de la distribución obtenida de las intensidades de rojo (estimación subpíxel).
5.3 Estimación de las Correspondencias
De la etapa anterior se tienen 2 conjuntos de puntos de las imágenes segmentadas. Como las imágenes se encuentran ordenadas de acuerdo al barrido realizado, se pueden segmentar un par de imágenes que corresponde a las 2 vistas de la línea de barrido en el mismo instante de tiempo.
A partir de la matriz F que ha sido calculada previamente en la calibración. Lo que se desea entonces, es encontrar las intersecciones de la línea segmentada con la línea epipolar en la segunda vista, haciendo uso de cada uno de los puntos que componen la línea segmentada de la primera imagen, para generar la correspondiente línea epipolar en la segunda vista. Las líneas epipolares en 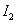 están dadas por
están dadas por 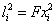 . El punto en la segunda imagen xi2, donde las líneas (epipolar
. El punto en la segunda imagen xi2, donde las líneas (epipolar 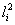 y línea de barrido) se intersecan, es una correspondencia de x i1. La Figura 7 ilustra la idea claramente.
y línea de barrido) se intersecan, es una correspondencia de x i1. La Figura 7 ilustra la idea claramente.
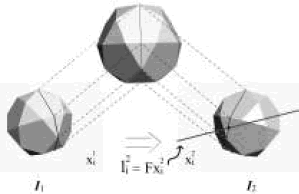
Figura 7. Geometría para la estimación de correspondencias.
Figure 7. Matched points´ estimation geometry.
La Figura 8(b) muestra las correspondencias estimadas de las imágenes reales de un teléfono. El número de puntos extraídos es 39145.

Figura 8. Correspondencias extraídas de dos vistas calibradas.
Figure 8. Extracted correpondences from two calibrated views.
5.4 Reconstrucción
Para este momento, se han definido 2 conjuntos de puntos de dimensiones iguales, cuyos elementos se relacionan uno a uno. Esto es a lo que se llama correspondencias, y su relación viene de la proyección de un ''único'' punto 3D, al menos para configuraciones no degeneradas. Este punto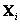 se proyecta sobre los planos de imagen (
se proyecta sobre los planos de imagen (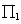 y
y 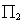 ) a los puntos
) a los puntos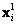 y
y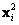 , respectivamente.
, respectivamente.
Se puede calcular la posición de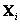 con un conjunto de ecuaciones dadas por las matrices de cámara
con un conjunto de ecuaciones dadas por las matrices de cámara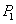 y
y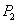 y puntos
y puntos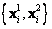 . Es posible reescribir las proyecciones
. Es posible reescribir las proyecciones 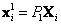 y
y 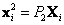 dentro de una ecuación matricial dada por,
dentro de una ecuación matricial dada por,
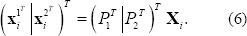
Esta ecuación es de la forma 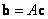 , por lo que su solución es
, por lo que su solución es 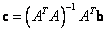 . Tal solución sería apropiada si las correspondencias estuviesen libres de ruido, pero dado que este no es caso, es necesario optimizar la triangulación de los puntos. La función de costo es similar a la Ecuación 5, la gran diferencia radica en que los parámetros de cámara no cambian durante el proceso por lo que sólo se optimiza las posiciones 3D. Los resultados obtenidos a partir de las correspondencias mostradas en Figura 8(b) se presentan en la Figura 9.
. Tal solución sería apropiada si las correspondencias estuviesen libres de ruido, pero dado que este no es caso, es necesario optimizar la triangulación de los puntos. La función de costo es similar a la Ecuación 5, la gran diferencia radica en que los parámetros de cámara no cambian durante el proceso por lo que sólo se optimiza las posiciones 3D. Los resultados obtenidos a partir de las correspondencias mostradas en Figura 8(b) se presentan en la Figura 9.
5.4.1 Consideraciones sobre la estimación 3D
Dentro de la estimación de los puntos 3D que conforman la superficie, es importante considerar los efectos que tiene el ruido en las imágenes, para la determinación de la precisión del sistema estéreo. Los puntos 3D 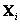 mapeados a las imágenes corresponden a las relaciones
mapeados a las imágenes corresponden a las relaciones 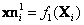 y
y 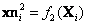 . Nótese que la diferencia fundamental de
. Nótese que la diferencia fundamental de 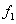 y
y 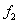 , con respecto a la operación de proyección
, con respecto a la operación de proyección 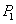 y
y 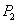 , es el resultado en coordenadas no homogéneas.
, es el resultado en coordenadas no homogéneas.

Figure9. Nube de puntos para estimación lineal y posterior optimización.
Figure 9. Cloud of points.
Consideremos un error de medición 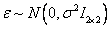 , para los puntos imágenes
, para los puntos imágenes 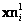 y
y 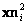 . Es posible mostrar que el error de estimación dado los errores de medición en las imágenes, está dado por:
. Es posible mostrar que el error de estimación dado los errores de medición en las imágenes, está dado por:
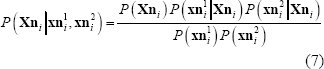
siendo
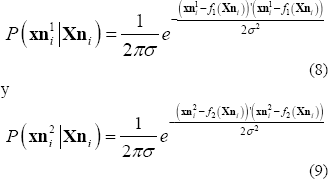
Además se consideran 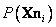 ,
, 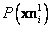 y
y
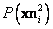 , como provenientes de distribuciones uniformes definidas por el espacio donde
, como provenientes de distribuciones uniformes definidas por el espacio donde 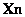 se mueve y las áreas de sus proyecciones dadas por los puntos
se mueve y las áreas de sus proyecciones dadas por los puntos 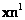 y
y 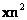 se acomodan. La Figura 10 muestra la densidad de probabilidad condicional sólo para variaciones del punto en el plano
se acomodan. La Figura 10 muestra la densidad de probabilidad condicional sólo para variaciones del punto en el plano 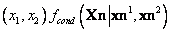 para las proyecciones
para las proyecciones 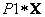 y
y 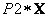 con
con 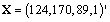 , con varianzas exageradas en el error de proyección, y cámaras que apuntan cerca del eje
, con varianzas exageradas en el error de proyección, y cámaras que apuntan cerca del eje 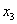 del sistema coordenado del mundo y están ubicadas en el en el cuadrante
del sistema coordenado del mundo y están ubicadas en el en el cuadrante 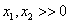 .
.

Figura 10. Densidad de probabilidad condicional 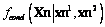 .
.
Figure 10. Conditional probability density 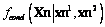 .
.
6. RESULTADOS
La confirmación del modelo de error propuesto se realiza mediante la adquisición de un plano paralelo al eje vertical del sistema mundo 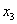 . Una buena aproximación para estimar la varianza del error de reconstrucción de los puntos con respecto a un plano perfecto, pude ser obtenida mediante el cálculo de distancias perpendiculares de los puntos reales a un plano obtenido por el truncamiento de la representación en valores singulares de la matriz
. Una buena aproximación para estimar la varianza del error de reconstrucción de los puntos con respecto a un plano perfecto, pude ser obtenida mediante el cálculo de distancias perpendiculares de los puntos reales a un plano obtenido por el truncamiento de la representación en valores singulares de la matriz 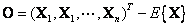 ; así, la varianza para el error corresponde al autovalor más pequeño de
; así, la varianza para el error corresponde al autovalor más pequeño de 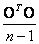 .
.
La Figura 11 deja ver la dirección principal del error de adquisición de una línea que se considera casi vertical para las mismas cámaras que generan la distribución de la Figura 10.
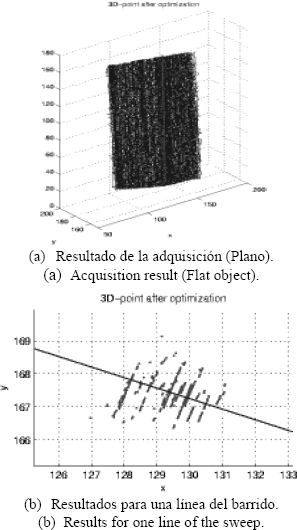
Figura 11. Puntos medidos.
Figure 11. Measured points.
Los errores obtenidos para esta configuración están alrededor de1 mm considerando errores en las correspondencias de hasta 2 píxeles.
La Figuras 12 y 13 exhiben algunos de los resultados para diferentes adquisiciones y con una densidad de puntos variable.
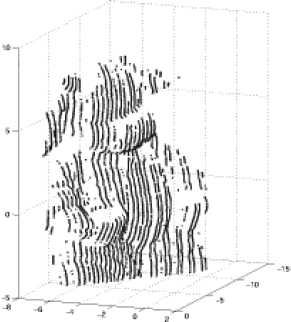
Figura 12. Vaca (figura de cerámica).
Figure 12. Cow (ceramic figure).
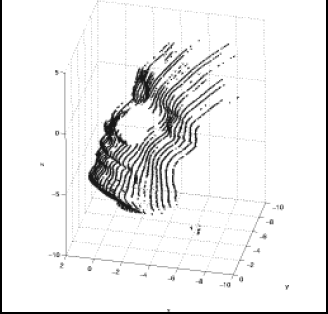
Figura 13. Cara.
Figure 13. Human Face.
7. CONCLUSIONES
En [4], se menciona como el uso de representaciones homogéneas en la optimización puede no ser recomendable ya que la dimensión agregada no representa un grado de libertad más en el problema. Sin embargo, durante la implementación dicha adición parece mejorar los resultados de la optimización al no llegar a mínimos locales que podrían aparecer al deshomogenizar el sistema coordenado de las soluciones iniciales obtenidas linealmente.
La presencia de ruido en las correspondencias estimadas hace indispensable el uso de alguna optimización en la estimación de los puntos 3D. El algoritmo para la validación de las correspondencias retuvo un número considerable de inliers, aproximadamente un tercio en proporción a los píxeles del área de interés.
Como trabajo futuro, se propone una mejora al algoritmo de segmentación de la línea proyectada, que podría basarse en algún criterio de análisis espacio tiempo, lo que viene ligado a un estudio más detallado de la fuente de luz empleada.
REFERENCIAS
[1] FRANCOIS BLAIS. Review of 20 years of range sensor development. Tecnical report, Nacional Research Council Canada Institute for Information Technology, 2004 [ Links ]
[2] RICHARD HARTLEY, RAJIV GUPTA AND TOM CHANG. Stereo from uncalibrated cameras. Pages 761–764, 1992. [ Links ]
[3] RICHARD I. HARTLEY, In defense of the eight-point algorithm. IEEE Transactions on pattern Analysis and Machine Intelligence, 19(6): 580–593, June 1997. [ Links ]
[4] RICHARD HARTLEY AND ANDREW ZISSERMAN. Multiple View Geometry in Computer vision. The Press Syndicate of the university of Cambirdge, second edition, 2003. [ Links ]














